基于ISAR像序列的多旋翼无人机参数估算

任枫轩，　王忠勇

(1.河南职业技术学院电气工程系，郑州　450046；　2.郑州大学信息工程学院，郑州　450001)

0　引言

由于多旋翼无人机具有良好的空中悬停特性及易控特性，在航拍、测绘、运输、安保等领域扮演着越来越

重要的角色[1-3],但由此也引发了许多安全问题。由于质量或操作的原因极有可能在人员密集的区域坠机而引发安全事故，多旋翼携载的可见光、红外、电磁等探测设备也使得隐私越来越容易被窥视，曾发生过无人机黑飞影响航班安全的事件，因此我国于2013年相继推出了民用无人机的空中管理条例，对无人机的航速、重量和飞行高度等都做出了相关要求。由于雷达电磁波受天气影响较小，在目标探测中发挥重要作用，雷达ISAR像为目标散射源在成像平面上的投影表征，可以最直观地反映目标的形态，在连续的ISAR像中更可以提取出目标的运动参数，为了对空中飞行的无人机进行更准确的识别，本文利用ISAR像序列对多旋翼目标进行探测[4]。目前公开发表的文献中几乎没有对多旋翼无人机特征参数的研究，但在利用ISAR像获取目标特征参数方面的研究较多。文献[5]通过仿射配准对ISAR像进行横向定标，再通过聚类算法提取强散射源，进而估算了目标长度特征；文献[6]分析了目标在成像平面上不随雷达参数变化的稳定特征量，建立ISAR像与结构参数的关系，提出了利用稳定特征量反估结构参数的方法；文献[7]分析了空间目标运动模型及成像机理，推导了强散射源在ISAR像平面上的理论分布，并以此来估算特征参数。为此，借助雷达二维像高分辨特征，采用ISAR像序列对多旋翼无人机的旋翼片数及转动周期进行识别，通过仿真实验验证了算法的有效性，且具有较低的估算误差。

1　多旋翼无人机运动模型

多旋翼无人机一般由4片以上的旋翼构成，每个旋翼由2片桨叶构成，旋翼轴对称分布且共面，为了对多旋翼无人机运动模型进行建模，首先以旋翼中心为原点，在旋翼旋转平面内任意方向为xrotor1轴，旋翼转动角速度矢量方向为zrotor1轴，按右手螺旋法则确定yrotor1轴，由此建立旋翼坐标系[8]，如图1所示。

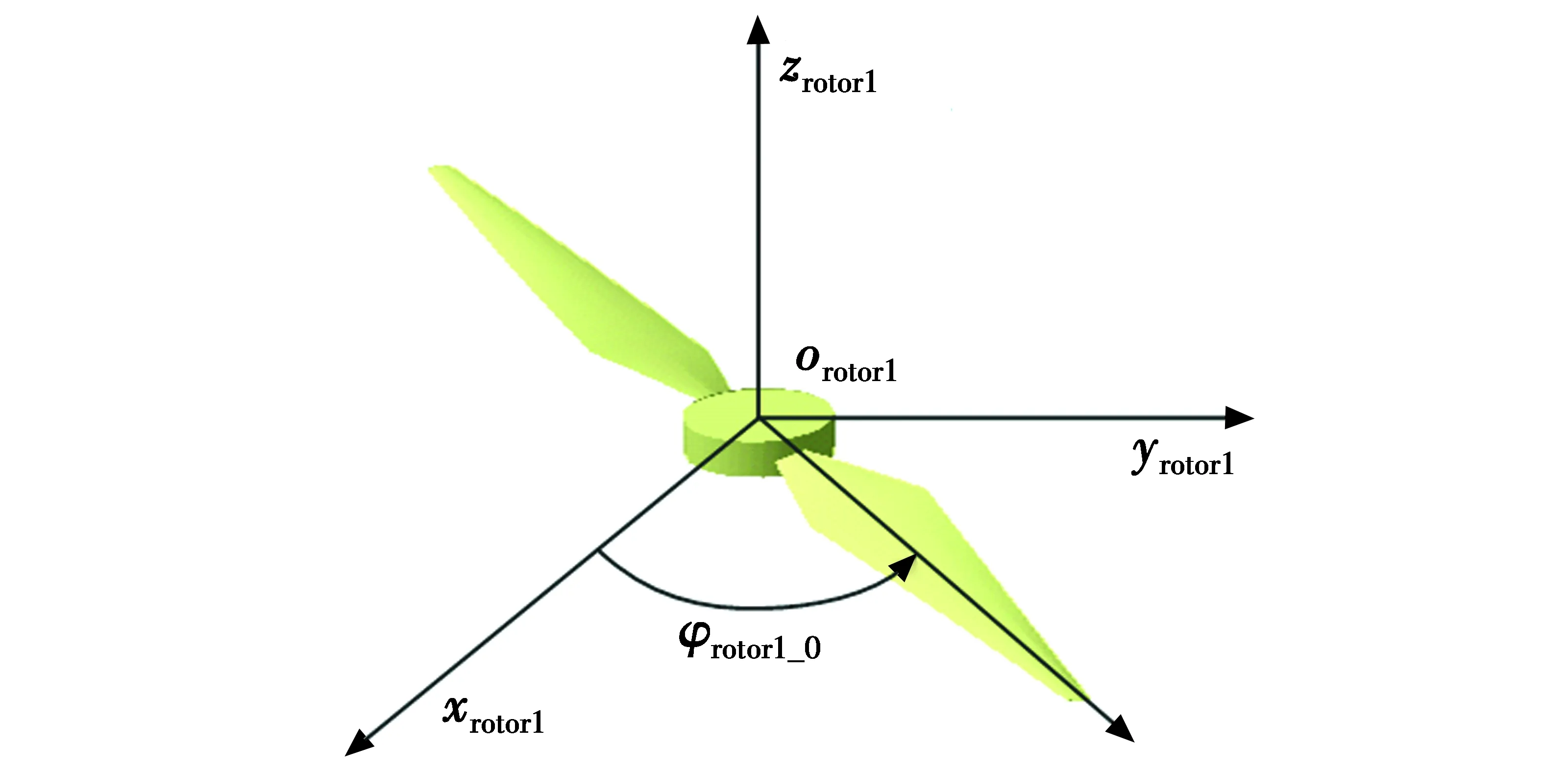
图1　旋翼坐标系Fig.1　Rotor coordinate system

图1中，φrotor1_0为旋翼在旋翼坐标系中的旋转角度，设旋翼旋转角速度为ωrotor1，且其初始转角为φrotor1_init_0，则φrotor1_0可表示为：φrotor1_0=φrotor1t+φrotor1_init_0。对旋翼上任意的散射源位置r0，在t时刻该散射源在旋翼坐标系下的位置r1可表示为

(1)

由于多旋翼无人机的各个旋翼共面且轴对称分布，所以在建立机体坐标系时以多旋翼无人机的对称轴为zbody轴，以各旋翼所在平面内任意方向为xbody轴，再由右手螺旋定则确定zbody轴，不失一般性，设桨叶片数为4，由此建立机体坐标系如图2所示。

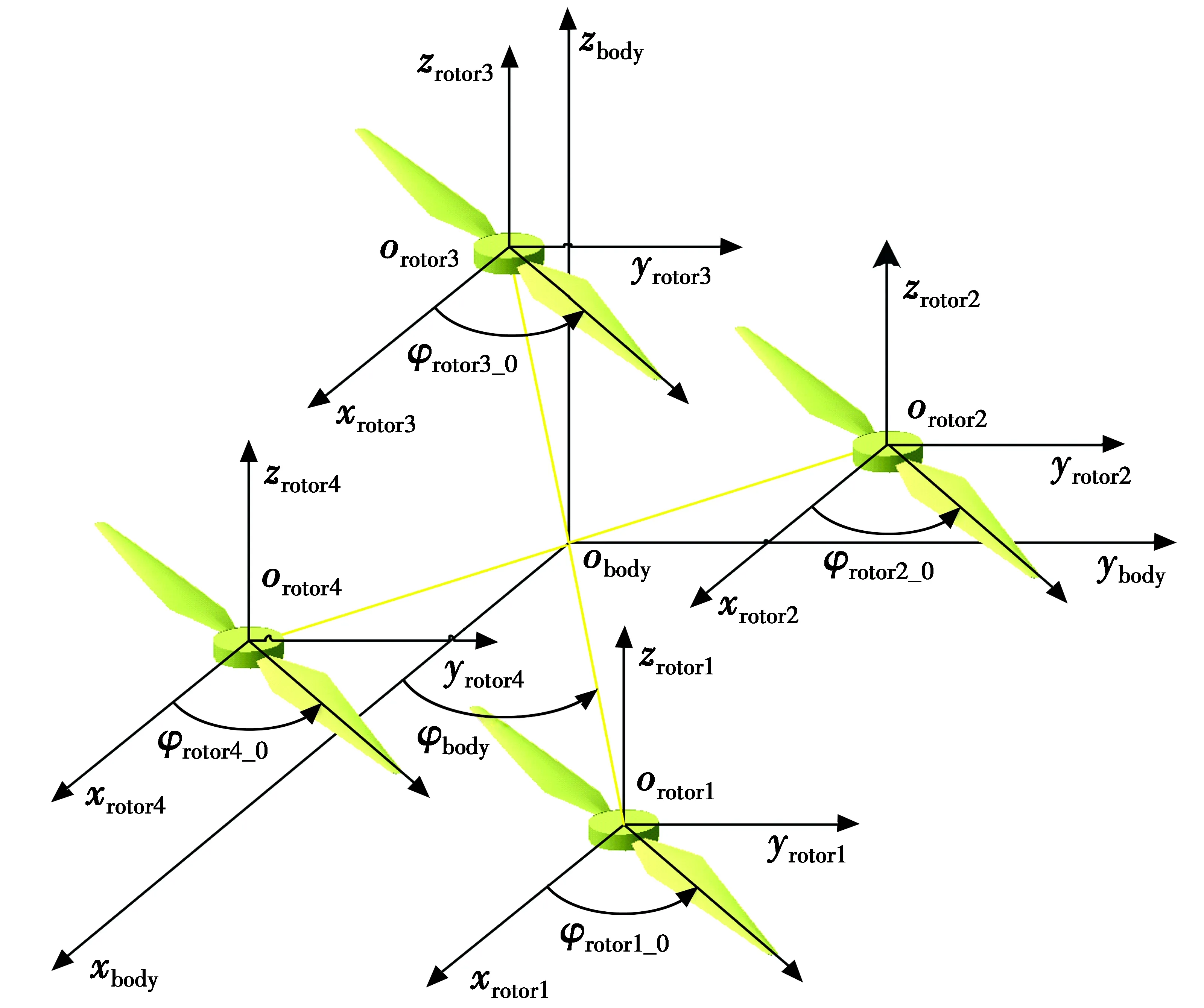
图2　机体坐标系Fig.2　Coordinate system of the aircraft body

图2中，φbody为多旋翼无人机在机体坐标系中的转动角度。设桨叶中心到zbody轴的距离为l，桨叶坐标系中的r1在机体坐标系下的坐标r2表示为

(2)

由于多旋翼机体存在俯仰、斜侧和旋转等运动，以机体中心为原点，以垂直于大地表面垂直向上为z轴，以过雷达视向与z轴构成的平面且垂直于z轴的直线为x轴，利用右手螺旋定则确定y轴[9]，los为雷达视向，由此构建本体坐标系如图3所示。

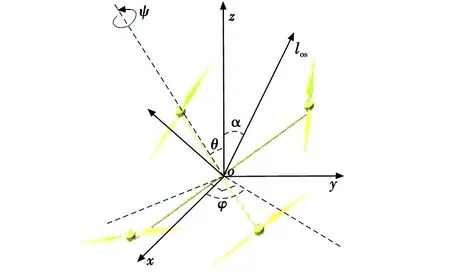
图3　本体坐标系Fig.3　Ontology coordinate system

不考虑平动运动，多旋翼的任意运动可用欧拉矩阵Rconi来表示[10]，令φ为锥旋角，θ为章动角，ψ为自旋角，则欧拉矩阵Rconi(t)可表示为

Rconi(t)=

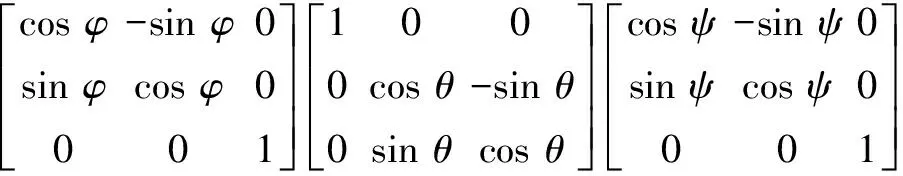
(3)

那么旋翼上r0处的散射源在本体坐标系下的坐标r可表示为

r=Rconi·r2。

(4)

2　多旋翼无人机ISAR像成像分析

由于多旋翼无人机在空中的运动轨迹复杂，各个旋翼转动速率较快，获取其整个旋转状态下回波的时间较短，即可认为在旋翼完成一周自旋的情况下多旋翼无人机机身相对于雷达视向的位置未变化，其机身自身的微动及桨叶快速旋转都使散射源微多普勒变动且桨叶成像转角积累较大，从而导致利用传统的距离-多普勒成像算法成像时会出现散焦现象，而时频分析技术的出现可以有效地解决由于多普勒时变引起的散焦现象，本文采用距离-瞬时多普勒成像算法完成多旋翼无人机成像[11]。

2.1　成像机理

设雷达发射线性调频信号，对回波做解线频调处理，通过FFT变换得到慢时间频率域的回波信息，忽略剩余视频项和包络斜置项，有[7]

Sif(tm,f)=

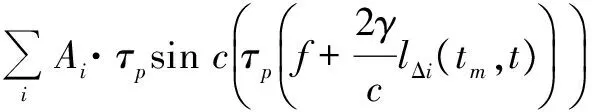
(5)

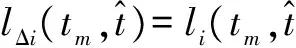
再对每个距离单元中的回波进行时频变换，采用Gabor变换对式(5)进行变换[12]，有

power(t,ω,l)=

(6)

上式选取特定的成像时间t，可获得t时刻散射源在雷达视向及多普勒轴上的散射能量分布，即ISAR像，如果选择连续的成像时间，则可获得连续的ISAR像分布。

2.2　成像仿真实验

设桨叶片数为4，桨叶半径为13 cm，桨叶中心到机体中心的距离l为0.6 m，第1片旋翼在机体坐标系中的转动角度φbody为30°，相应的第2片到第4片旋翼

在机体坐标系中的转动角度为120°，210°，300°，设第1片旋翼旋转角速度ωrotor1为10π，且其初始转角φrotor1_init_0为0°；第2片旋翼旋转角速度ωrotor2为10π，且其初始转角φrotor2_init_0为120°；第3片旋翼旋转角速度ωrotor3为10π，且其初始转角φrotor3_init_0为250°；第4片旋翼旋转角速度ωrotor4为10π，且其初始转角φrotor4_init_0为330°，雷达视向与z轴之间的夹角α为45°，机身欧拉角中的锥旋角φ为40°，章动角θ为20°，自旋角ψ为30°；设雷达带宽为4 GHz，起始频率为8 GHz，脉冲重复频率100 kHz，脉宽640 μs，信噪比为30 dB，快时间域采样点数为64，慢时间域采样点数为3200，回波仿真方法采用物理光学法，对回波数据的距离域及多普勒域进行10倍插值后，提取慢时间域长度为0.2 s内的目标回波数据，将其分成0.2/25 s的时间间隔依次提取ISAR像，对多旋翼无人机ISAR像进行仿真，结果如图4所示。共得到25幅图像，第1行由左向右依次是第1～5幅ISAR像，第2行由左向右依次是第6～10幅ISAR像，依次类推，且竖向为多普勒轴，相应的窗长为[-781.25 Hz，781.25 Hz]，横向为距离向轴，相应的窗长为[-1.2 m，1.2 m]。

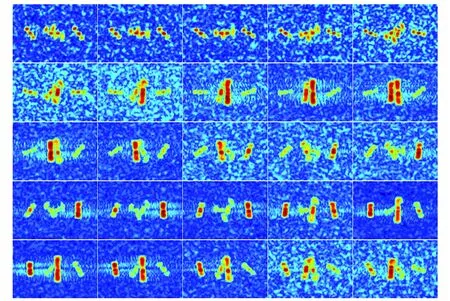
图4　慢时间域成像间隔为0.2/25 s的成像结果Fig.4　Results of slow time domain imaging at a interval of 0.2/25 s

从仿真结果可以发现，桨叶中心位置始终位于0 Hz处，而从雷达视向看去，多旋翼各个桨叶的旋转中心并不在一条直线上，这是由于ISAR像横向是由多普勒来决定的，由于在短时间内假设多旋翼机体运动速度为0，所以每个桨叶中心位置处的运动速率为0，故在成像平面上桨叶的中心位置处始终位于0 Hz处；同时，不难发现当雷达视向与桨叶垂直时，桨叶的散射最强(对应以上各幅ISAR像中的粗竖线)，且桨叶散射最强时，各桨叶在多普勒轴上的分布长度是不同的，这是由于各个桨叶的转动速度不同引起的多普勒分布不同，如果对各个桨叶分别进行横向定标，那么获取的各

个桨叶的尺寸是相同的。

3　旋翼数量及各桨叶转速估算

当雷达视向与桨叶垂直时会出现强散射，由此可以提取旋翼数量及桨叶转速。对ISAR像数据进行预处理，得到强散射在时间-距离向上的分布，再从中提取特征参数。

3.1　数据预处理

利用人眼观测连续的ISAR像序列可以直接获取桨叶片数，本文要实现桨叶片数的参数化估算，当桨叶垂直于雷达视向时，桨叶散射最强，设此时对应的时间序列为i，将对应的ISAR像强度分布矩阵Ii中的元素按距离单元依次求和，得到第i个时间序列散射强度沿距离像序列的分布向量li，即

li=sum(Ii)

(7)

不难发现，向量li应该在含有桨叶的那几个距离单元中的幅值最高，如果将所有时刻的li汇总成一个矩阵LT，则

LT=(l1l2…lN)N×M

(8)

即LT为N×M维的矩阵，其中，N为时间序列的总数，M为距离向单元数。将采样时间改为0.4 s，ISAR像成像时间间隔改为0.4/200 s，获取相应的LT矩阵并绘于图5中。

图5　LT矩阵分布Fig.5　LT matrix distribution

3.2　特征提取

从图5可看出，图中黑色圆圈处均存在极大值点(rs,ts)，假设极大值点数为S，s取值范围为1,…,S。如果已经提取出黑色圆圈处的极大值点在距离向上的投影rs，那就可以确定桨叶片数，并可以提取相应的LT(n,rs/Δr)，其中，n为时间序列标号，取值范围为1,…，N，Δr为距离分辨率，rs/Δr为相应的距离分辨单元标号。对LT(n,rs/Δr)进行自相关[13-14]处理获得的周期的2倍，即该桨叶的转动周期

T=2*corr(LT(n,rs/Δr))

(9)

式中，corr表示做自相关处理获取周期。

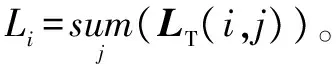
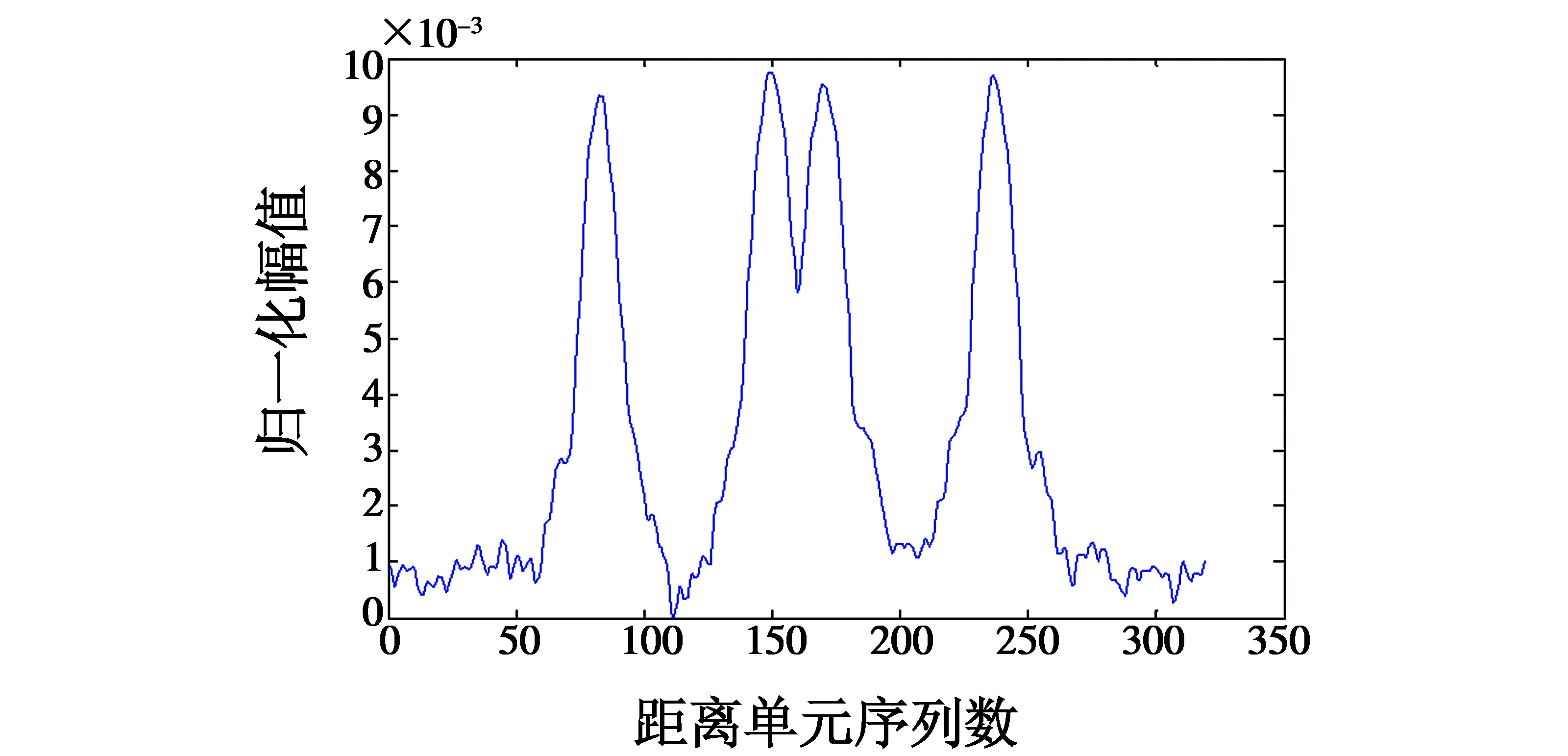
图6　向量L的归一化分布Fig.6　Normalized distribution of vector L

从图6中可以看出，L是一个多峰值分布的向量，其峰值个数及峰值位置分别是桨叶片数及桨叶在雷达视向上的位置。为了实现参数化提取，引入基本的蚁群算法[15]提取极大值点位置。但向量L中除了桨叶中心的位置处出现峰值外，在其他峰谷区域内存在许多局部极大值点，这是由于噪声引起的，而基本的蚁群算法无法对此进行区分，可通过设定阈值的方式来进行筛选，不失一般性，令η·max((rs,ts),s=1,…,S)为阈值，其中，η为筛选系数，取值范围为0～1，由此可以确定桨叶片数及桨叶中心在雷达视向上的投影位置，再依据前面的方法可以获得桨叶转动周期。

4　仿真结果分析

对旋翼数目及旋翼转动周期进行估算，需设置的仿真参数有修正系数η取0.8，基本蚁群算法的仿真参数设置如下：蚂蚁数量为1000、蚂蚁移动次数为50、信息素挥发系数为0.8、转移概率常数为0.2、筛选系数为0.8，蚁群算法搜索获取的极大值[16]结果如图7所示。

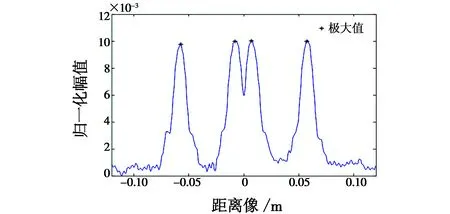
图7　蚁群算法搜索获取的极大值结果Fig.7　Maximum results of ant colony algorithm search

图7满足条件的极大值共有4个，相应的雷达视向投影分别为-0.057 m，-0.007 m，0.007 m，0.057 m，提取矩阵LT中相应距离单元上的向量，分别列于图8中。对图8中的4个向量分别用式(9)中的方法进行周期估算，估得周期分别为0.212 s，0.216 s，0.200 s，0.204 s。相应的误差分别为6%，8%，0%，2%。再考虑雷达视角α分别取30°，45°及60°，且信噪比分别取30 dB，20 dB，10 dB，0 dB的情况，将桨叶片数及桨叶转动周期估算误差列于表1。

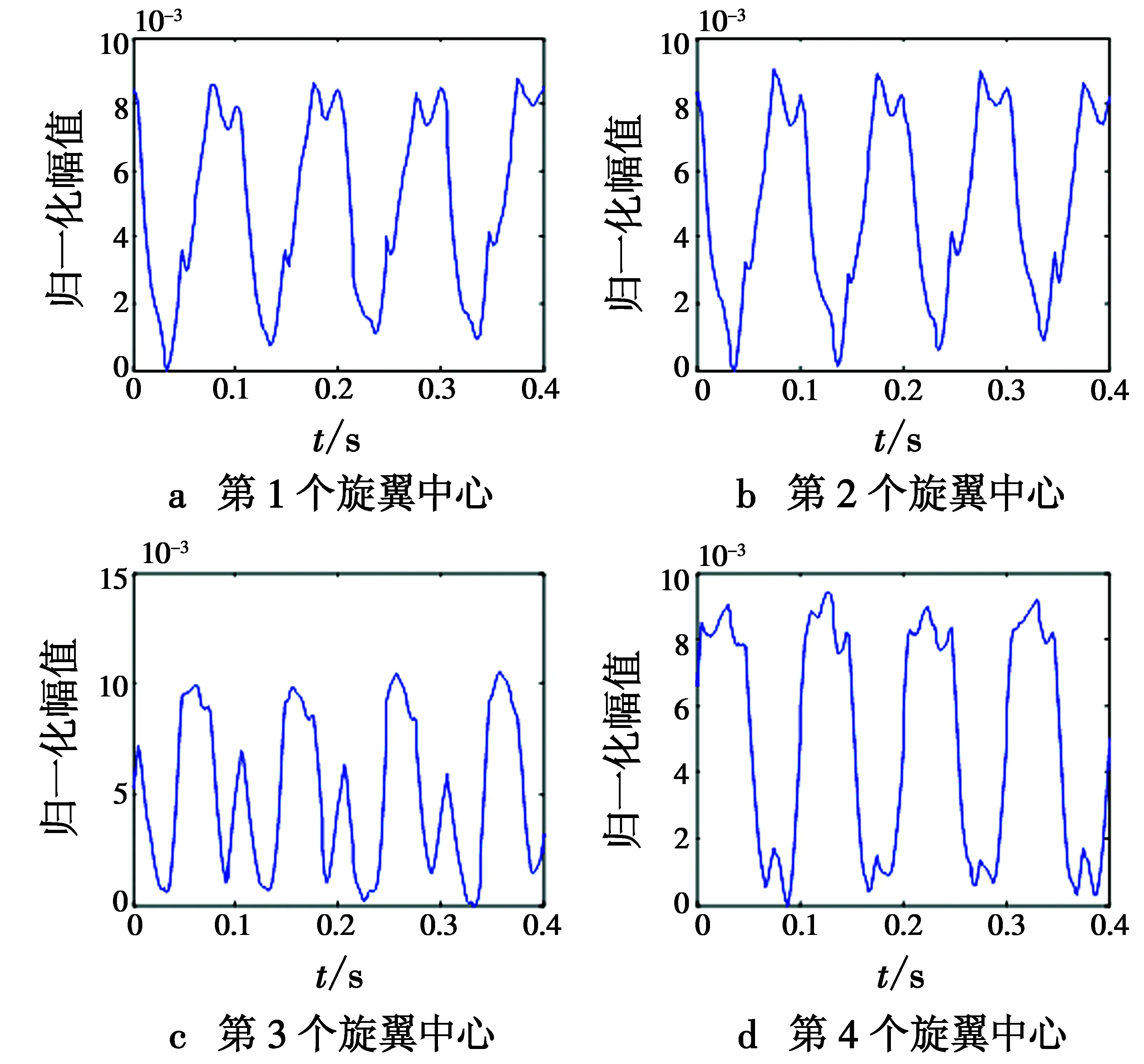
图8　提取的矩阵LT中相应距离单元上的向量分布Fig.8　Vector distribution on the corresponding distance unit in the extracted matrix LT

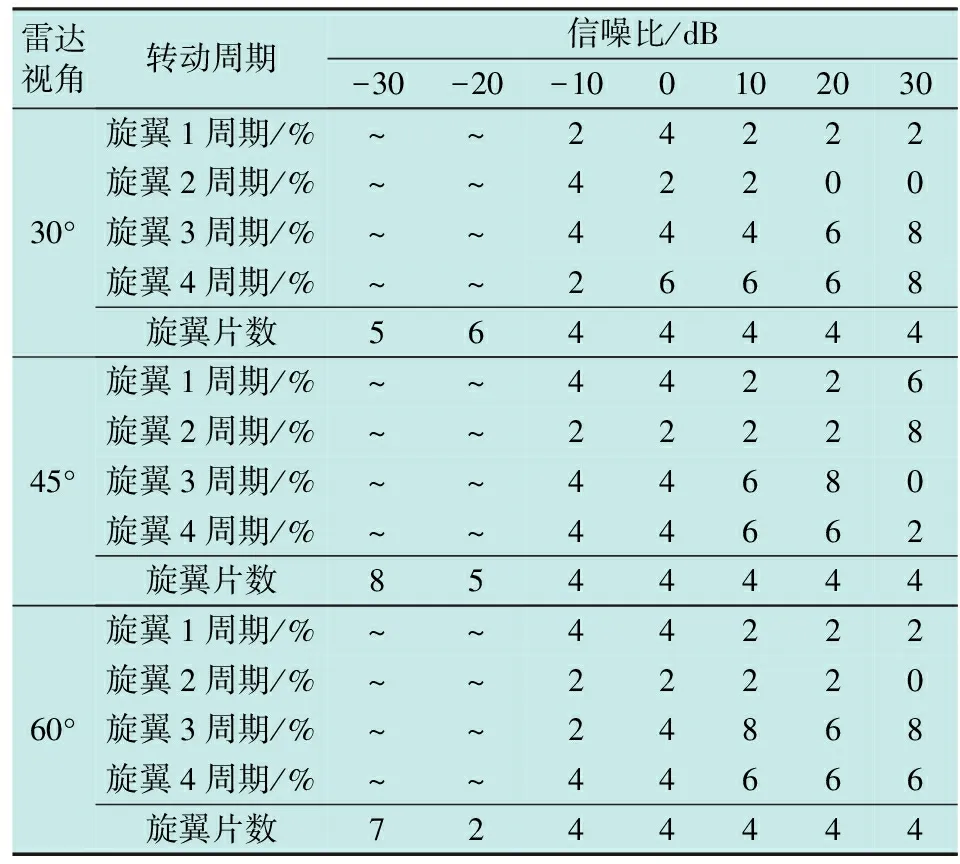
雷达视角转动周期信噪比/dB-30-20-10010203030°旋翼1周期/%～～24222旋翼2周期/%～～42200旋翼3周期/%～～44468旋翼4周期/%～～26668旋翼片数564444445°旋翼1周期/%～～44226旋翼2周期/%～～22228旋翼3周期/%～～44680旋翼4周期/%～～44662旋翼片数854444460°旋翼1周期/%～～44222旋翼2周期/%～～22220旋翼3周期/%～～24868旋翼4周期/%～～44666旋翼片数7244444

由仿真结果可以看出，在信噪比大于-10 dB的情况下，旋翼数目及各旋翼转动周期均可有效估算，并且旋翼转动周期估算误差小于8%；而在信噪比低于-20 dB时，由于旋翼数估算错误，致使提取出的周期与真实值差别较大，所以并未列出此时的周期估算误差。另外，发现表中所有的周期估算误差的百分数都是2的整数倍，这是由于ISAR像采样间隔导致的，本文ISAR像采样间隔为0.4/200=0.002 s，那么对提取的时间序列进行自相关处理后的时间分辨率也为0.002 s，由式(9)可知估算的周期分辨率为0.004 s，除以真实周期0.2 s，可得周期估算的百分数分辨率为2。

5　结束语

借助雷达二维像高分辨特征，利用ISAR像序列提取旋翼强散射特征进行参数估算，通过对多旋翼无人机运动模型建模，对多旋翼无人机ISAR像成像机理分析，再利用强散射在时间及雷达视向上的分布，结合蚁群算法及自相关对多旋翼无人机的旋翼片数及其转动周期进行估计。通过仿真实验结果表明：当信噪比大于-10 dB时，各个参数估算误差不会超过8%，这说明提出的算法可有效提取相应参数，对飞行的旋翼无人机的探测识别提供了有力的数据支持，为低空安全管理提供保障。

[1]戴冬,王果,王磊.博弈论在固定翼无人机地面目标跟踪控制中的应用[J].计算机工程,2016,42(7):287-292,298.

[2]高扉扉,陈念年,范勇,等.一种旋翼式无人机的视觉着陆位姿估计方法[J].电光与控制,2017,24(2):35-38,80.

[3]王庆贺,万刚,曹雪峰,等.基于数据融合的多旋翼无人机定位控制器设计[J].系统仿真学报,2016,28 (10):2593-2599.

[4]张凌晓,王宝顺,贺思三,等.基于图像旋转匹配的组网雷达ISAR图像横向定标[J].计算机工程与科学,2015,37(4):796-801.

[5]JIN G H,GAO X Z,DONG Z.Two-dimensional length extraction of ballistic target from ISAR images using a new scaling method by affine registration[J].Defence Science Journal,2014,64(5):458- 463.

[6]徐少坤,刘记红,袁翔宇,等.基于ISAR图像的中段目标二维几何特征反演方法[J].电子与信息学报,2015, 37(2):339-345.

[7]束长勇,陈世春,吴洪骞,等.基于ISAR像序列的锥体目标进动及结构参数估计[J].电子与信息学报,2015,37(5):1078-1084.

[8]陈丽城,李春涛,张孝伟,等.无人机地面动力学建模及分析[J].计算机仿真,2016,33(6):13-18,35.

[9]刘东辉,奚乐乐,孙晓云.矢量拉力垂直起降无人机姿态纵向控制研究[J].计算机工程与应用,2017,53(1):260-264.

[10]XU S K,LIU J H,WEI X Z,et al.Wideband electromagnetic characteristics modeling and analysis of missile targets in ballistic midcourse[J].Science China Technolo-gical Sciences,2012,55(6):1655-1666.

[11]芮力,钱广红,张国庆,等.基于自适应最优核时频分布理论的ISAR成像方法[J].电光与控制,2014,21(7):46-50,102.

[12]ÖZDEMIR C.Inverse synthetic aperture radar imaging with MATLAB algorithms[M].New York:John Wiley & Sons,2012:274-287.

[13]周磊磊,罗炬锋,付耀先,等.低信噪比下基于自相关函数的频率估计方法[J].华中科技大学学报:自然科学版,2014,42(4):45- 49.

[14]陈刚,王鹏飞,李金玲.基于自相关函数的模糊时间序列优化算法[J].控制与决策,2015(10):1797-1802.

[15]DORIGO M,DI CARO G.Ant colony optimization:a new meta-heuristic[J].Proceedings of the Congress on Evolutionary Computation,1999.doi:10.1109/CEC.1999.782657.

[16]武光辉,童创明,李西敏,等.逆合成孔径雷达目标成像识别优化仿真[J].计算机仿真,2016,33(6):9-12,339.