四旋翼飞行器姿态的非奇异快速终端滑模控制
2018-04-19罗连杰佃松宜
罗连杰, 佃松宜, 蒲 明
(1.四川大学电气信息学院,成都 610065; 2.成都信息工程大学控制工程学院,成都 610225)
0 引言
近年来,随着四旋翼飞行器在军用和民用领域被广泛应用,其控制问题成为了研究热点之一[1-4]。由于四旋翼飞行器系统中存在模型不确定性以及外界未知干扰,故要求其控制系统具有较强的鲁棒性。滑模控制因其具有强鲁棒性,而被广泛应用于四旋翼飞行器姿态控制问题[5-6]。文献[7]利用自适应律估计外界干扰的上界,结合反演法和滑模控制设计鲁棒控制
器,实现了飞行姿态的稳定跟踪控制。文献[8]为实现飞行姿态的快速跟踪,设计了快速终端滑模控制器,提高了飞行姿态的跟踪速度,同时采用改进的趋近律去除了控制抖振。在四旋翼飞行器姿态的滑模控制器设计中,往往是通过增大切换增益值来处理不确定,但较大的控制增益一方面易造成控制抖振,另一方面易使控制输入饱和,引入观测器实时估计系统不确定和外界干扰可有效解决上述问题。文献[9]引入非线性干扰观测器估计外界干扰,并将估计值引入滑模控制器中,提高了姿态跟踪精度。文献[10]将由系统不确定和外界干扰组成的复合扰动视为扩张状态,采用扩张状态观测器进行估计,降低了切换增益,进而抑制了控制抖振。但文献[9-10]中观测器的观测误差均是渐近收敛的,收敛速度较慢。为此,本文设计有限时间干扰观测器以实现对系统不确定和外界未知干扰的快速精确估计。
在前人研究的基础上,本文以存在模型参数不确定和外界未知干扰的四旋翼飞行器姿态跟踪控制问题为研究对象,基于有限时间干扰观测器设计滑模控制器。采用有限时间干扰观测器实现对复合扰动的快速精确估计,并将观测值引入控制器设计中进行补偿。结合非奇异快速终端滑模控制设计鲁棒控制器,提高系统跟踪误差收敛速度的同时去除了控制抖振,基于Lyapunov理论证明了系统跟踪误差一致最终有界,最后通过仿真验证了所提方法的可行性和有效性。
1 四旋翼飞行器的模型
四旋翼飞行器坐标如图1所示。
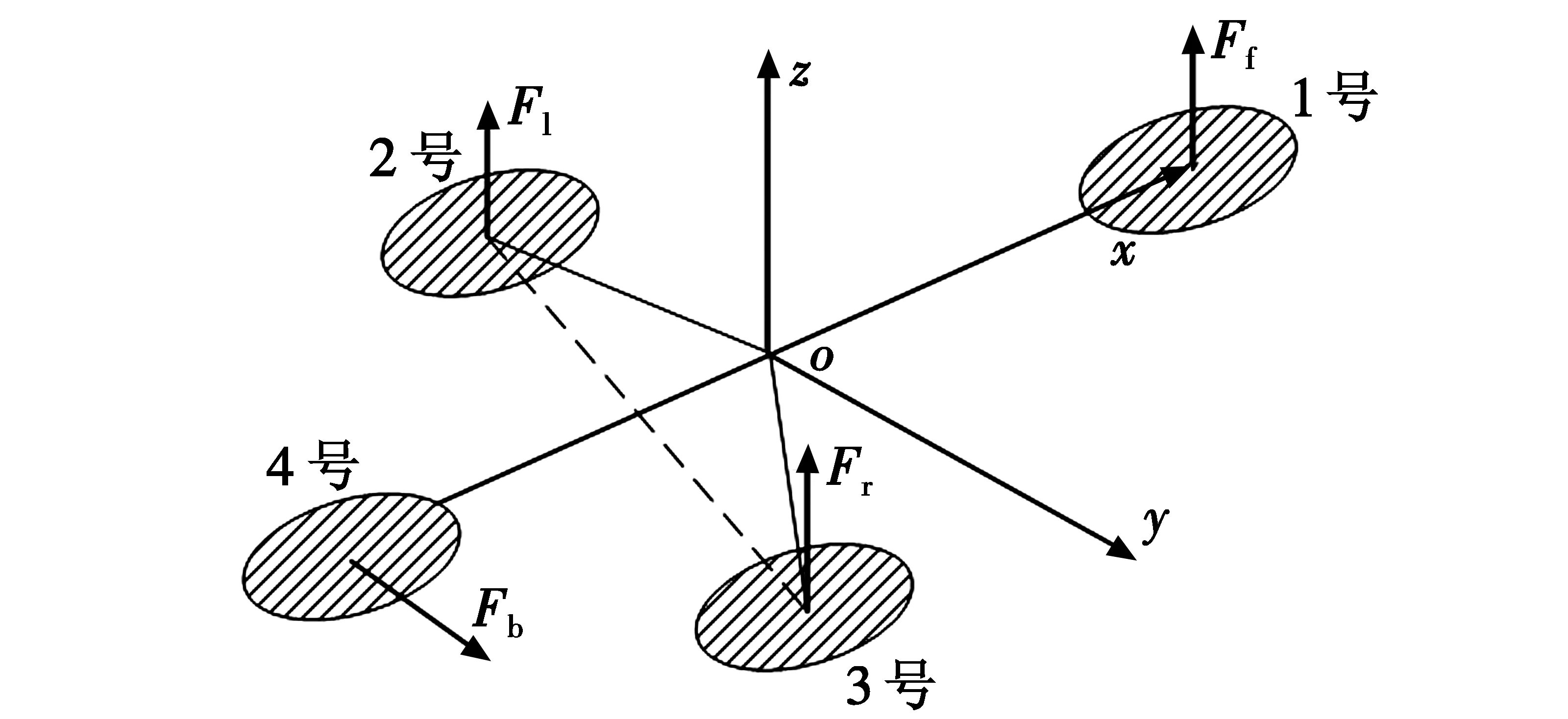
图1 四旋翼飞行器力学坐标Fig.1 Mechanical coordinates of quadrotor aircraft
参考文献[7],四旋翼飞行器的俯仰角、滚动角、偏航角以及高度平衡方程为
(1)
式中:P,R,Y和Z分别为俯仰角、滚动角、偏航角以及高度;Uf,Ur,Ul和Ub分别表示前、右、左、后4个电机的输入电压,即系统的控制量;Kf c为力系数;Lf为前螺旋桨中心到y轴的距离;Jp,Jr和Jy分别为四旋翼飞行器绕y轴、x轴和z轴的转动惯量;m为四旋翼飞行器的质量;g为重力加速度。代入四旋翼飞行器的物理参数并化简得
(2)

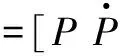
(3)
式中,di(i=1,…,4)为未知有界复合扰动。
假设1di(t)有界但上界未知,其一阶导数存在且有界,即
(4)
式中,Li为未知正常数。
本文的控制目标是针对存在复合扰动的四旋翼飞行器系统设计鲁棒控制器,使各通道输出稳定跟踪理想的输入信号,其中,输入信号光滑有界。为简化控制器设计步骤,以俯仰角通道为例,进行控制器设计。
2 有限时间干扰观测器设计
为实现对复合扰动的快速精确估计,设计如下形式的有限时间干扰观测器[11]
(5)
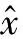
3 控制器设计

(6)
式中:γ=g/l,λ=p/q,p,q,g,l均为正奇数,且1<λ<2,γ>λ;a和b为已知正常数。
当系统状态远离平衡位置时,角度跟踪误差e1的高幂次项起主要作用,此时系统能快速收敛到平衡位置附近,此后角度跟踪误差的一阶导数e2起主要作用,保证系统误差以较快速度收敛到零。由于γ和λ均大于1,避免了对滑模面求导时出现负指数项,即避免了终端滑模的奇异问题。
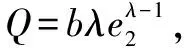
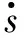
(7)
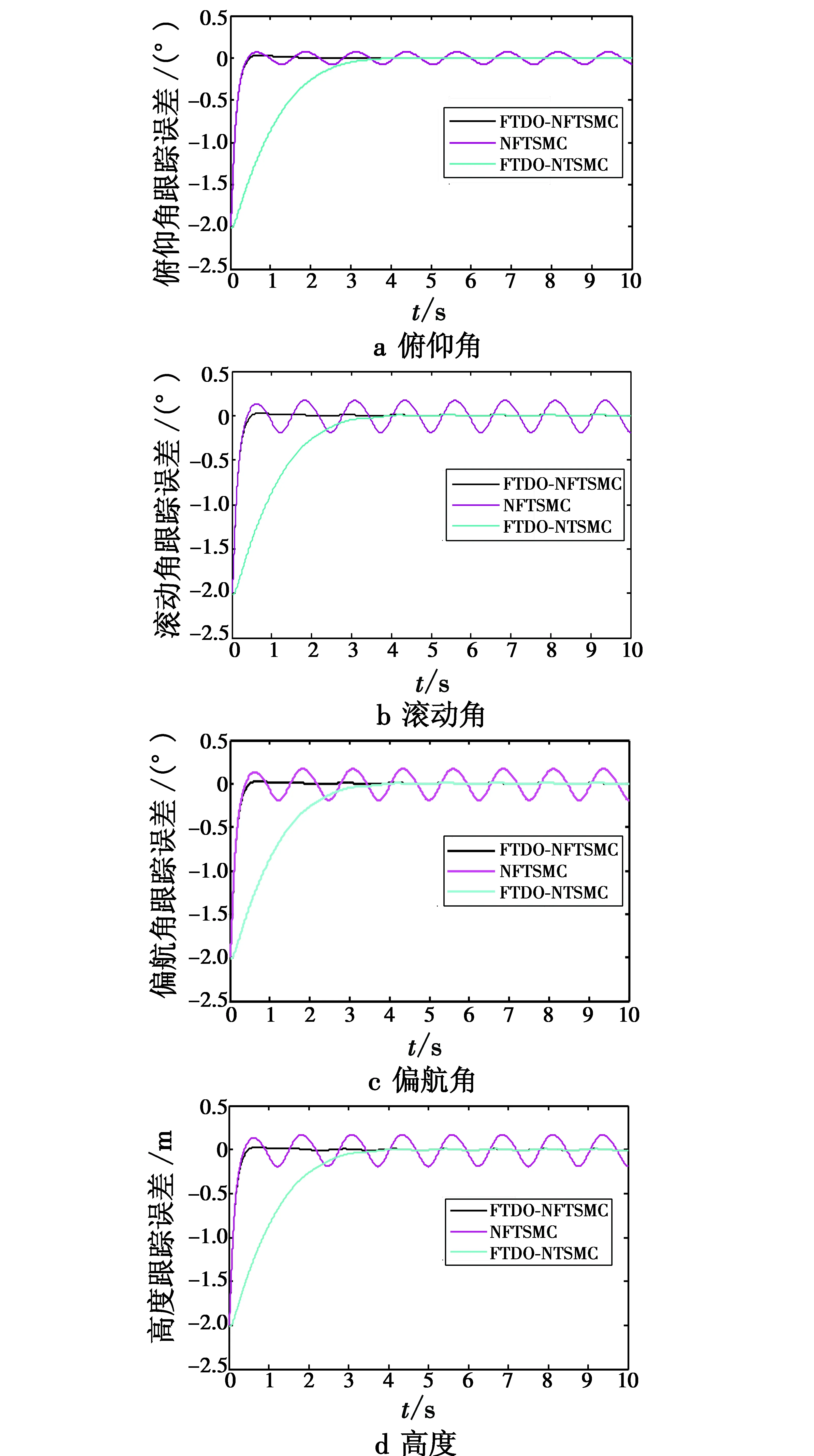
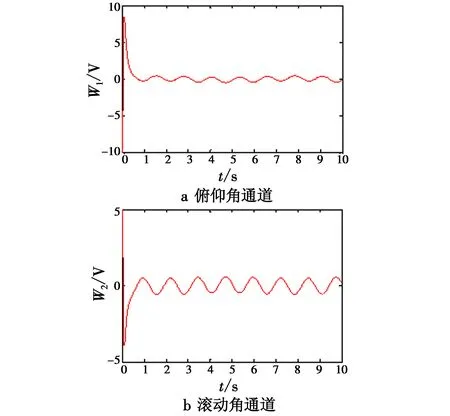
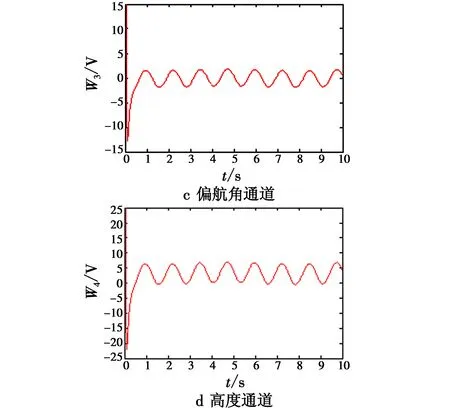
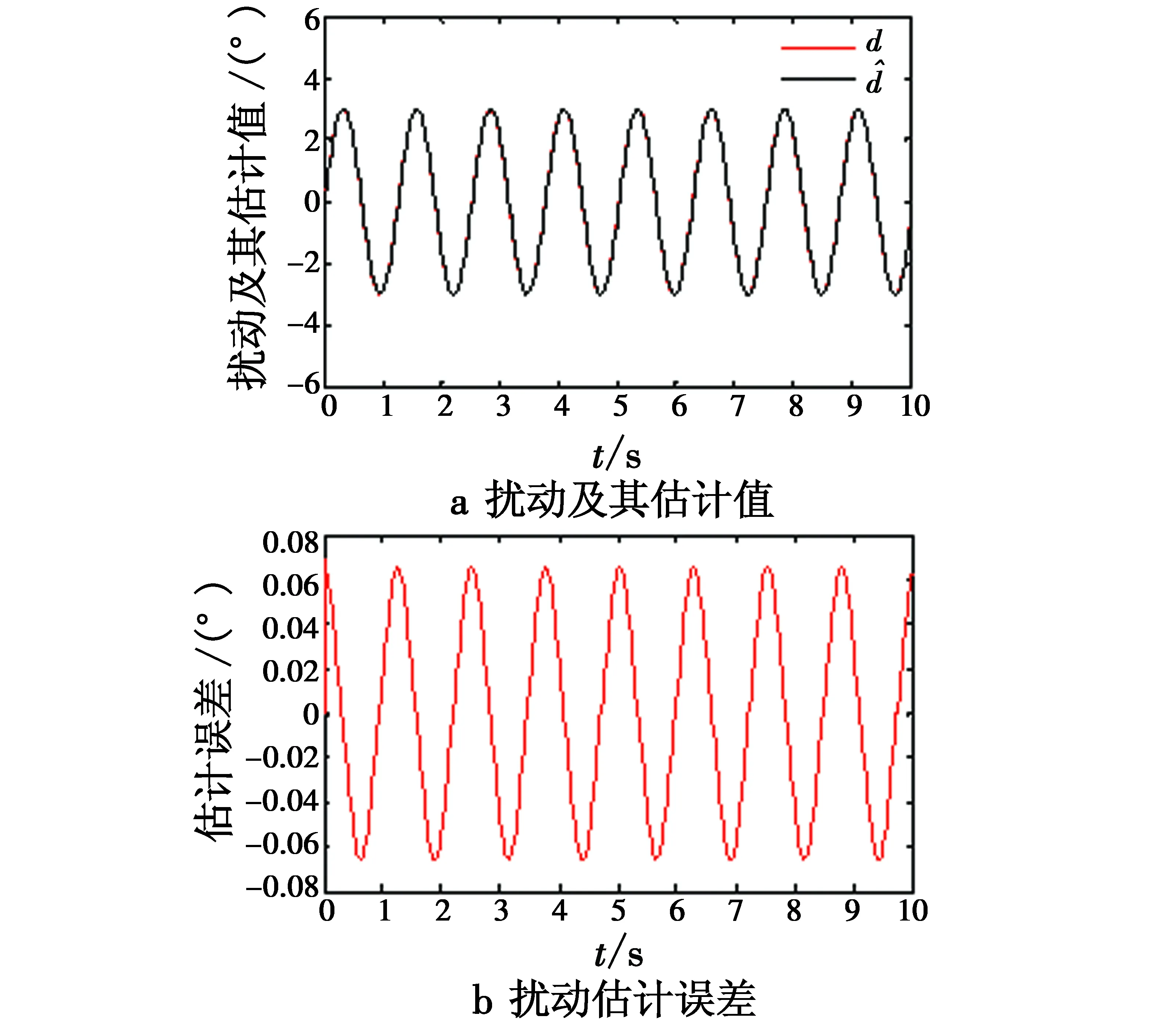
式中:k,μ,η均大于零;f,h,m,n为正奇数,且0 综合式(6)、式(7)俯仰角通道的控制律设计为 (8) 同理可得滚动角、偏航角和高度通道的控制律为 (9) (10) (11) 式中:滚动角通道跟踪误差e3=x3-xrd;偏航角通道跟踪误差e4=x5-xyd;高度通道跟踪误差e5=x7-xzd。 定理1对于含有复合未知扰动的四旋翼飞行器系统即式(3),在满足假设1的条件下,设计有限时间干扰观测器如式(5),选取非奇异快速终端滑模面如式(6),采用控制律如式(8)~式(11),则系统跟踪误差一致最终有界。以俯仰角通道为例,证明如下。 定义Lyapunov函数为 (12) 对V求导得 (13) 对s求导得 (14) 将式(8)代入式(14)得 (15) (16) (17) 对上式两边同乘eηt得 (18) 由上式知V(t)一致最终有界,则s一致最终有界。由式(6)可得俯仰角跟踪误差e1一致最终有界。同理可得系统所有跟踪误差均一致最终有界。 将四旋翼飞行器系统分为俯仰、滚动、偏航以及高度4个通道系统,各通道理想输入信号为x1d=x2d=x3d=x4d=sint,各通道初值为xp0=xr0=xy0=xz0=(-20)T,扰动选择为di=3sin 5t,i=1,…,4。其余控制系统参数选取为λ1=30,λ2=150,a=8,b=1,q=7,p=9,g=5,l=3,k=5,f=7,g=5,μ=0.5,m=3,n=5,η=6。 为验证本文控制方法的优越性,分别设计了基于有限时间干扰观测器(Finite-Time Disturbance Observer,FTDO)的非奇异终端滑模(Non-Singular Terminal Sliding Mode Control,NTSMC)控制器和无FTDO的非奇异快速终端滑模(Non-Singular Fast Terminal Sliding Mode Control,NFTSMC)控制器与本文控制器进行仿真对比。 从图2跟踪误差效果对比可以看出,在没有FTDO观测扰动并在控制器中进行补偿时,系统的跟踪误差较大;而引入FTDO后,控制精度有明显提高,同时还可以看出采用NFTSMC方法的控制器相比采用NTSMC方法的控制器,系统跟踪误差的收敛速度明显加快。由图3知引入终端吸引子后,控制输入基本平滑,较好抑制了控制抖振。由图4可以看出,FTDO实现了对扰动的快速精确估计,估计误差一致最终有界。 图2 跟踪误差对比图Fig.2 Tracking error comparison 图3 各通道控制输入Fig.3 Control input of each channel 图4 FTDO观测效果Fig.4 Observation results of FTDO 本文针对四旋翼飞行器姿态控制问题中系统存在模型参数不确定和外界未知干扰的情况,设计有限时间干扰观测器对复合扰动进行有限时间估计,并基于估计值设计非奇异快速终端滑模控制器,引入终端吸引子设计趋近律,抑制了控制抖振。仿真结果表明,本文所提方法提高了系统的跟踪速度和跟踪精度,同时去除了控制抖振,便于实际应用。 [1]ABDESSAMEUD A,TAYEBI A.Global trajectory tracking control of VTOL-UAVs without linear velocity measurements[J].Automatica,2010,46(6):1053-1059. [2]YANG K S,CHENG C C.Robust adaptive controller design for a quadrotor helicopter[J].Applied Mechanics & Materials,2013,284:2296-2300. [3]DYDEK Z T,ANNASWAMY A M,LAVRETSKY E.Adaptive control of quadrotor UAVs:a design trade study with flight evaluations[J].IEEE Transactions on Control Systems Technology,2013,21(4):1400-1406. [4]XIONG J J,ZHENG E H.Position and attitude tracking control for a quadrotor UAV[J].LSA Transactions,2014, 53(3):725-731. [5]薛劭哲,侯明善,张松.微型四旋翼飞行器TSMC控制方法研究[J].电子设计工程,2013,21(15):88-91. [6]PATEL A R,PATEL M A,VYAS D R.Modeling and analysis of quadrotor using sliding mode control[C]//Proceeding of the 44th Southeastern Symposium on System Theory,2012:111-114. [7]曹开发,谢慕君,李元春.基于自适应反演滑模的四旋翼飞行器姿态控制研究[J].自动化与仪表,2016,22(1):42- 47. [8]吴文海,刘锦涛,李静,等.四旋翼无人机SO(3)快速终端滑模姿态控制器设计[J].电光与控制,2015,22(11):6-10. [9]杨柳,刘金琨.基于干扰观测器的四旋翼无人机轨迹跟踪鲁棒控制[J].飞行力学,2015,33(4):328-333. [10]吴琛,苏剑波.四旋翼飞行器的轨迹跟踪抗干扰控制[J].控制理论与应用,2016,33(11):1422-1430. [11]卜祥伟,吴晓燕,陈永兴,等.基于非线性干扰观测器的高超声速飞行器滑模反演控制[J].控制理论与应用,2014,31(11):1473-1479. [12]蒲明,吴庆宪,姜长生,等.高阶滑模微分器的分析与改进[J].控制与决策,2011,26(8):1136-1146. [13]李慧洁,蔡远利.基于双幂次趋近律的滑模控制方法[J].控制与决策,2016,31(3):498-502.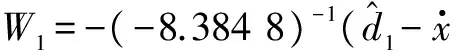
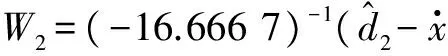
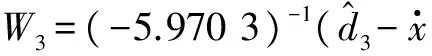

4 稳定性分析
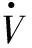
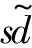
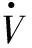
5 仿真分析
6 结论
