四旋翼飞行器静态H∞输出反馈控制

丁　力，　李兴成，　冯俊萍，　李尚荣，　计鹏程

(江苏理工学院机械工程学院，江苏 常州　213001)

0　引言

随着空中机器人技术的发展，四旋翼飞行器被广泛应用于工业生产，如建筑现场测绘与管理、电力巡线、桥梁架线、农田喷雾等[1-2]。然而，四旋翼是一个

强耦合、欠驱动、非线性的多输入多输出系统，要实现其稳定控制具有很大的挑战。因此，开发高精度、高性能的四旋翼飞行控制系统是工业领域和学术领域共同关心的热点。

为解决上述问题，SALIH A L等[3]将四旋翼动力学模型划分成俯仰、横滚、偏航与高度4个通道，设计了4个PID控制器实现各个通道的稳定控制；JAFARI H等[4]提出了一种基于LQR的四旋翼位姿控制器，通过求解Riccati方程获得反馈增益，实现四旋翼的状态反馈控制。近年来，研究人员发现在稳定位姿控制的基础上，当四旋翼受到内外部集总干扰影响时，其动力学模型也会随之改变[5]。如何以有效的控制策略来补偿集总干扰已成为四旋翼技术研究的重点。CABECINHAS D等[6]提出了一种非线性自适应状态反馈控制器来补偿集总干扰的影响，实现了四旋翼跟踪“8”字型轨迹；在获得精准模型的基础上，DONG W等[7]利用扩张观测器实现对系统状态及集总干扰的准确估计，并设计级联式比例控制器保证四旋翼在低速条件下的稳定飞行。

本文另辟蹊径，借鉴新加坡国立大学陈本美教授提出的静态H∞输出反馈控制算法[8]设计了四旋翼飞行器的位姿控制器。然而，对于该控制算法增益的求解，大多数迭代算法需要一个稳定的初始增益，这对于实际系统是很难实现的。因此，陈教授团队采用Riccati方程来求解增益[9]，虽然提高了计算效率，但求解精度并不是很理想，往往会陷入局部最优值。本文在获得四旋翼线性模型的基础上，采用静态H∞输出反馈控制算法分别设计姿态和位置两环控制器，并尝试利用布谷鸟算法(Cuckoo Search，CS)求解各控制环的输出反馈增益。最后，通过仿真算例验证了所提控制算法的有效性。

1　动力学建模

四旋翼飞行器通常被当作六自由度单刚体进行建模[10]，其结构如图1所示，包括4个旋翼产生的拉力fi(i=1,2,3,4)和力矩Mi(i=1,2,3,4)、姿态角η=[φθψ]T、位置量ε=[xyz]T、总拉力u=[f1f2f3f4]T和重力mg。

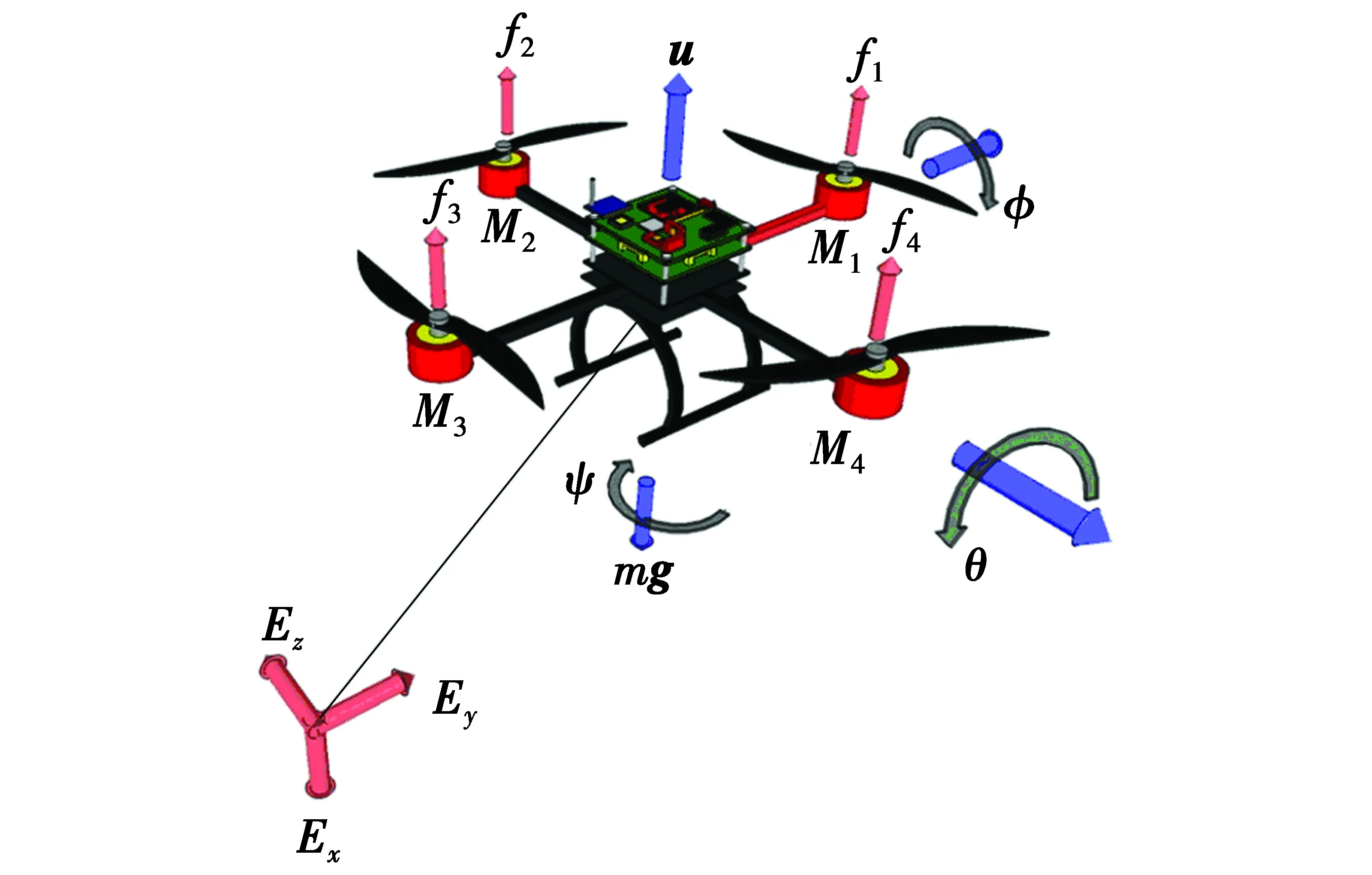
图1　四旋翼飞行器结构图Fig.1　Structure of quad-rotor aircraft

定义Euler-Lagrangian方程为

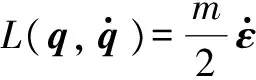
(1)

式中:ν=[pqr]T为角速度;q=[xyzφθψ]T为广义坐标;I为惯性矩阵。

通过带广义力的Euler-Lagrangian方程可推导出四旋翼的动力学模型，即

(2)

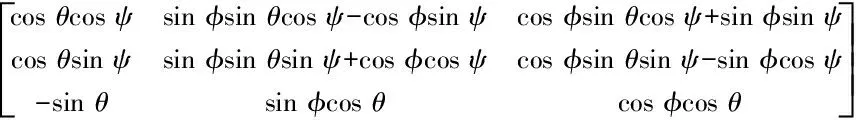
(3)

为了便于本文所提控制算法的设计，需获得上述模型的线性形式，故假设在四旋翼悬停配平处偏航角很小，即ψ≈0。最终，四旋翼飞行器的动力学模型可表示为

(4)

四旋翼系统的状态变量为

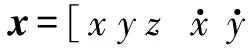
(5)

进而，可将式(5)改写成

x=[xyzuvwψθφrpq]T。

(6)

式中，u，v，w为三轴线速度。

2　飞行控制器设计

2.1　静态H∞输出反馈控制理论

对于如图2所示的线性时不变系统，其静态输出反馈控制律为u=-Ky=-KCx。在该系统中，若存在增益K使得Riccati方程渐进稳定，则(A,B)稳定；若存在矩阵L使得A-LC稳定，则(A,C)可观。因此，要使得该系统输出反馈稳定，则必然存在增益K使得A-BKC稳定。

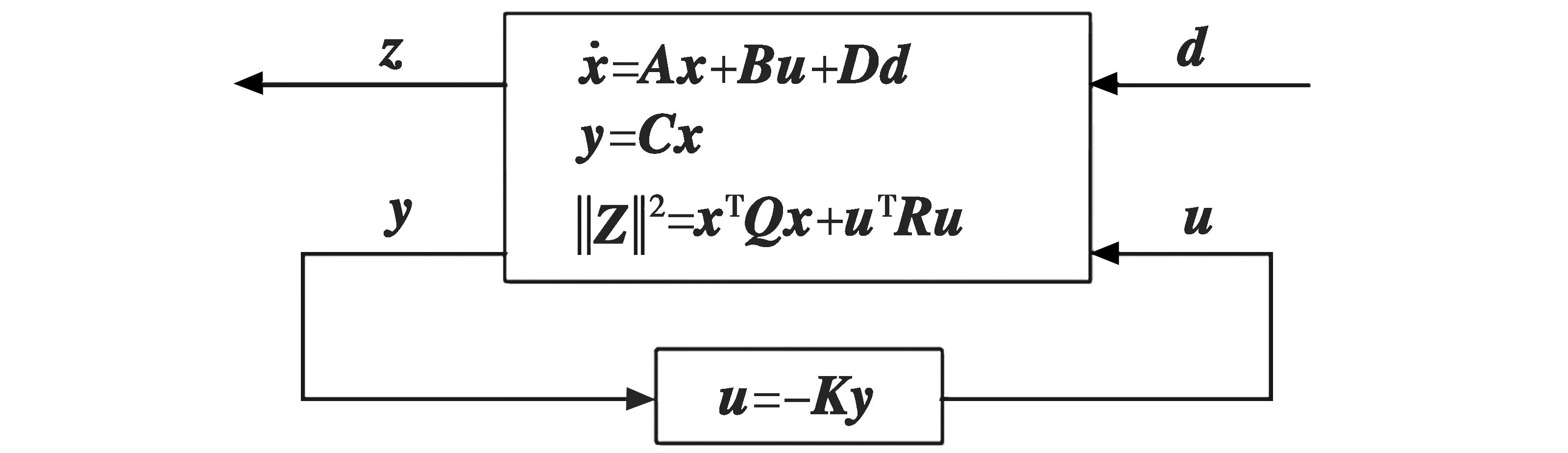
图2　线性时不变系统Fig.2　Linear time-invariant system

2.2　L2增益设计问题

通常，带干扰闭环系统的输出能量对干扰信号的抑制能力可以用L2增益来描述[11]。定义

(7)

式中，γ>γ*，γ*为最小增益。当γ=γ*时，则该系统的控制问题可被转换成H∞控制问题。本文采用CS算法来求解增益K使得系统稳定且L2增益以γ为界。

H∞输出反馈控制2.3CS算法描述

CS算法是由英国学者YANG X S[12]提出的一种模拟布谷鸟巢寄行为和Lévy飞行行为的新启元算法。在算法中，每个巢中的卵代表增益K的一个可行解，寻优的思想是利用潜在优解来代替巢中的劣解。

CS算法采用局部随机搜索和全局搜索的方式来寻找最优解。其中，局部搜索的方程为

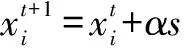
(8)

算法中的全局搜索由Lévy飞行决定，即

(9)

式中，α>0为缩放因子,λ为常数。

算法中的目标函数为

(10)

式中：α，ε，β与σ为调节参数；ts为调节时间；os为超调量。

算法具体流程如图3所示。

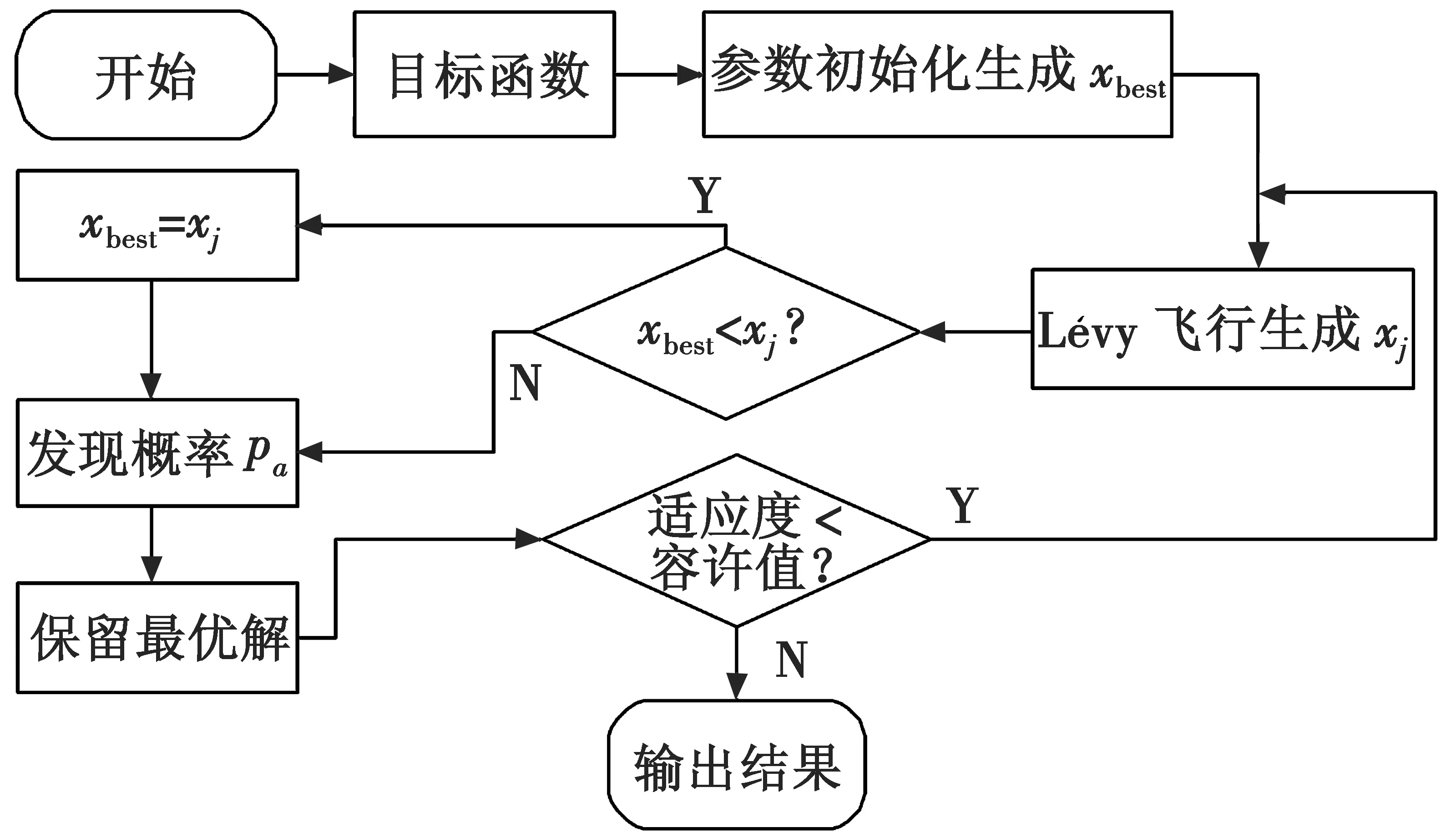
图3　CS算法流程图Fig.3　Flow chart of CS algorithm

2.4　姿态控制器设计

在四旋翼飞行器控制器的姿态环中，需要稳定的变量主要有俯仰角和滚转角，另外，作为姿态环额外的测量量，三轴角速度也需要被镇定，因此，姿态环的被控量为yin=[φθpqr]T。姿态环的状态空间方程为

(11)

式中:Din为阵风扰动输入矩阵;din为机身坐标系X轴与Y轴上的阵风扰动速度向量。阵风扰动模型可由Gauss-Markov方程产生[13]

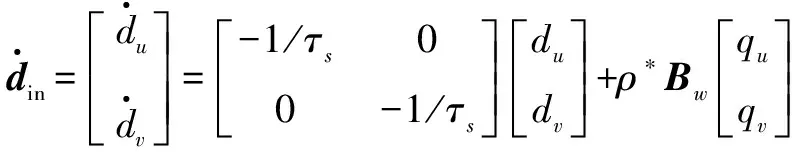
(12)

式中:ρ*为干扰系数；Bw为干扰输入矩阵;qu和qv为零均值噪声信号;τs为与风速相关的时间常数，若本文设定纵横向风速为5 m/s，则τs=3.2 s。

图4给出了姿态环的控制结构，其中，输出反馈增益Kin可由CS算法优化求得，具体来讲就是通过CS算法极小化目标函数Fi的值，从而找到一个最优或次优的增益矩阵。进而，可计算出姿态环的静态输出反馈控制率为

uin=-Kinyin+U。

(13)

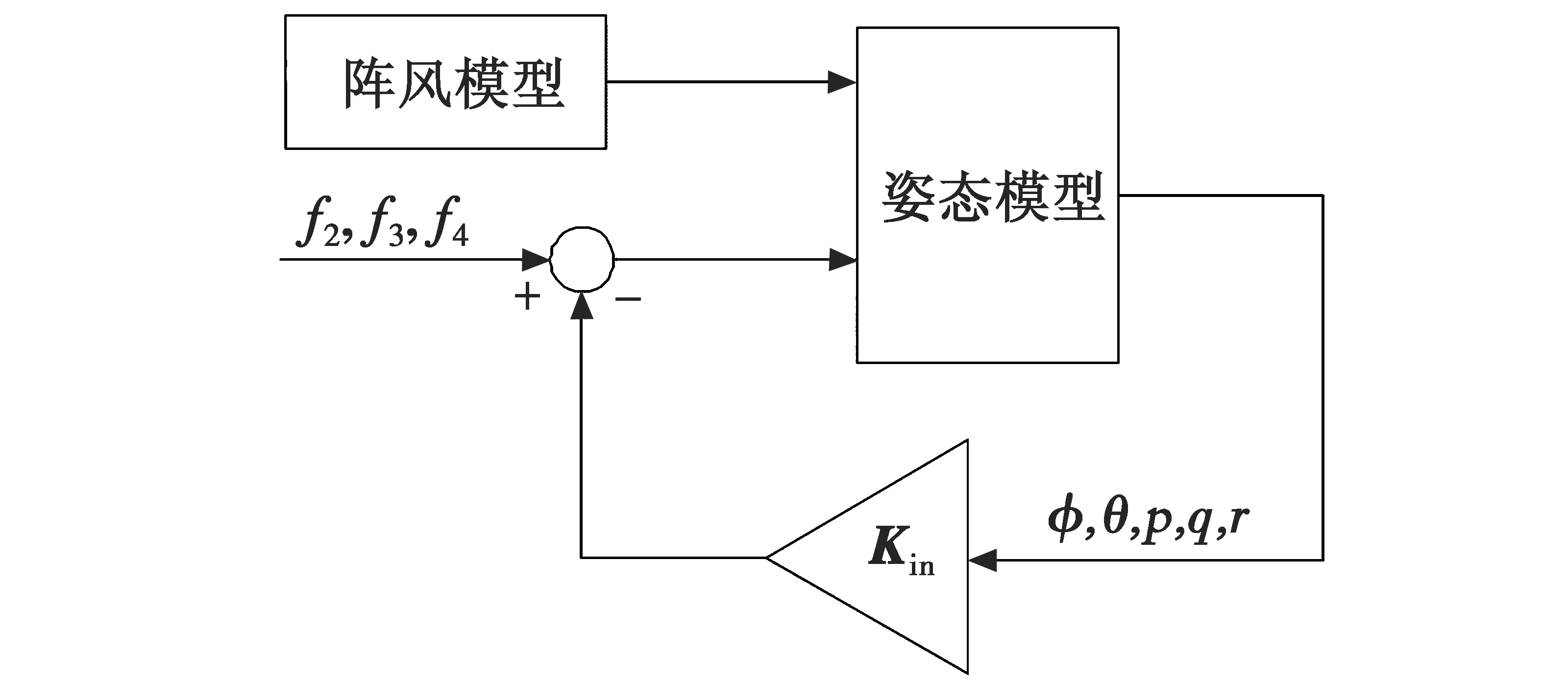
图4　姿态环控制框图Fig.4　Control structure of attitude loop

2.5　位置控制器设计

在四旋翼飞行器控制器的位置环中，需要稳定的变量为三轴位置、三轴线速度以及偏航角。因此，位置环的被控量为yo=[xyzuvwψ]T。

若不计阵风扰动的影响，姿态环的状态空间方程为

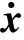
(14)

根据式(11)可得系统矩阵Aic=Ain-BinKinCin。

当俯仰角与滚转角很小时，位置环方程可近似为

(15)

因此，整个四旋翼系统的控制量为

xa=[φθpqruvwψ]T。

(16)

若能找到一个矩阵H满足

(17)

联立式(14)和式(16)就能得到

(18)

若考虑阵风扰动的影响，则式(18)可改写成

(19)

位置环的静态输出反馈控制律可由CS算法求得

uic=-Koyr

(20)

式中，yr=[(x-Xr) (y-Yr) (z-Zr)uvw(ψ-ψr)]T。输出反馈增益Ko可由CS算法优化求得，求解的过程与增益Kin的相同。

综上所述，四旋翼飞行器位置环控制如图5所示。

图5　位置环控制框图Fig.5　Control structure of position loop

3　数值仿真

为验证本文所提控制策略的有效性，在本算例中，控制四旋翼去跟踪预定的阶跃信号(Xr,Yr,Zr)=(1 m,0.8 m,0.5 m)，仿真时间持续10 s。为了模拟集总干扰的影响，除了在姿态环中加入阵风扰动，在位置环的测量端加入幅值为0.1的白噪声信号，仿真结果如图6所示。

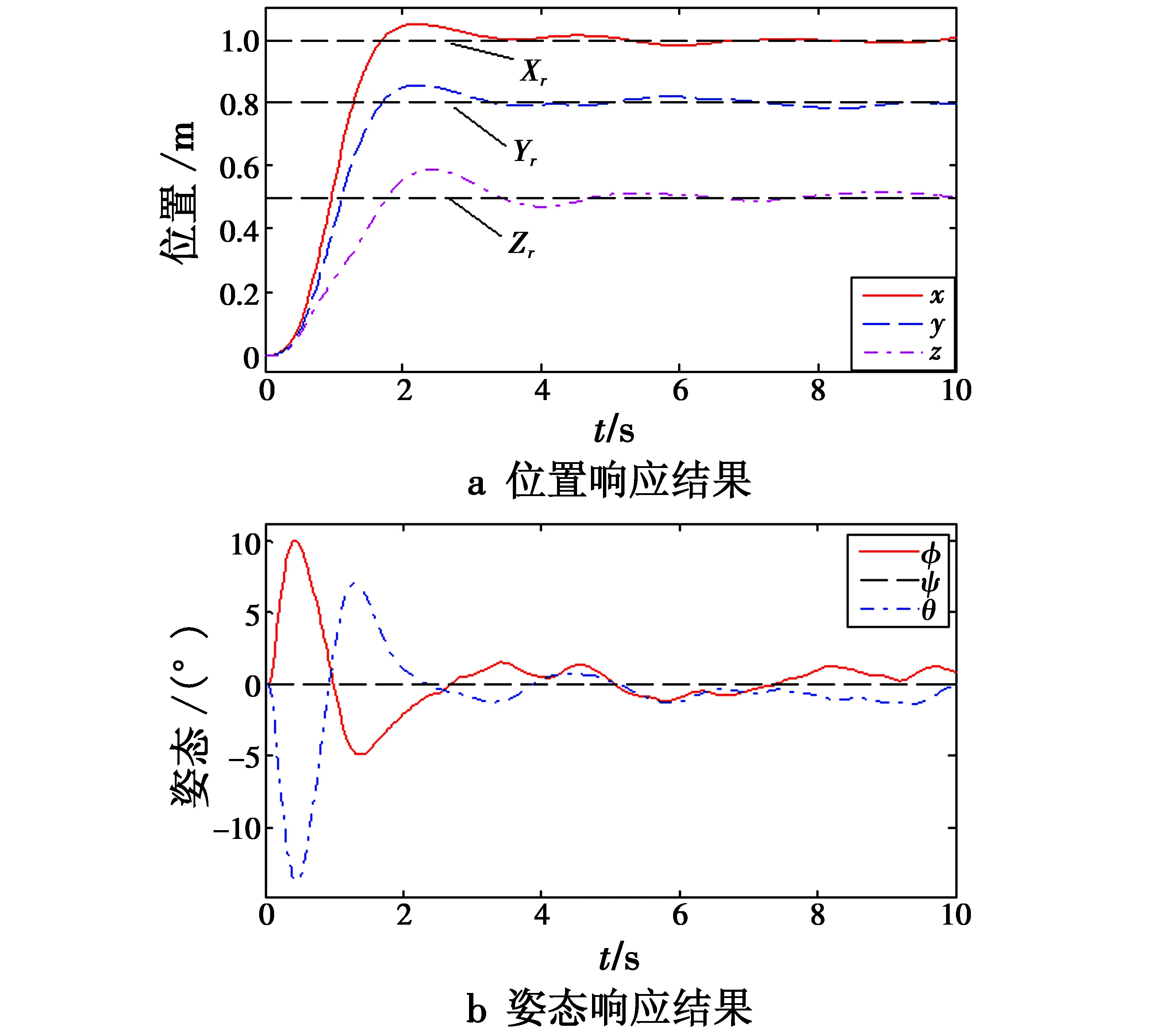
图6　仿真结果Fig.6　Simulation result

从图中可以看出，三轴位置均能在4 s内跟踪上预定信号，三轴姿态均能在3 s内被镇定住，即姿态环响应速度快于位置环响应速度，这表明了本文控制结构的合理性；三轴位置的最大超调量不超过20%，最大稳态误差不超过9%，这表明本文控制算法具有较强的抗干扰能力。

求解输出反馈增益时，先优化姿态环的增益，再优化位置环的增益，CS算法优化的迭代曲线如图7所示。需要指出CS算法的收敛性证明可由Markov模型来证明[14]，本文不再赘述。

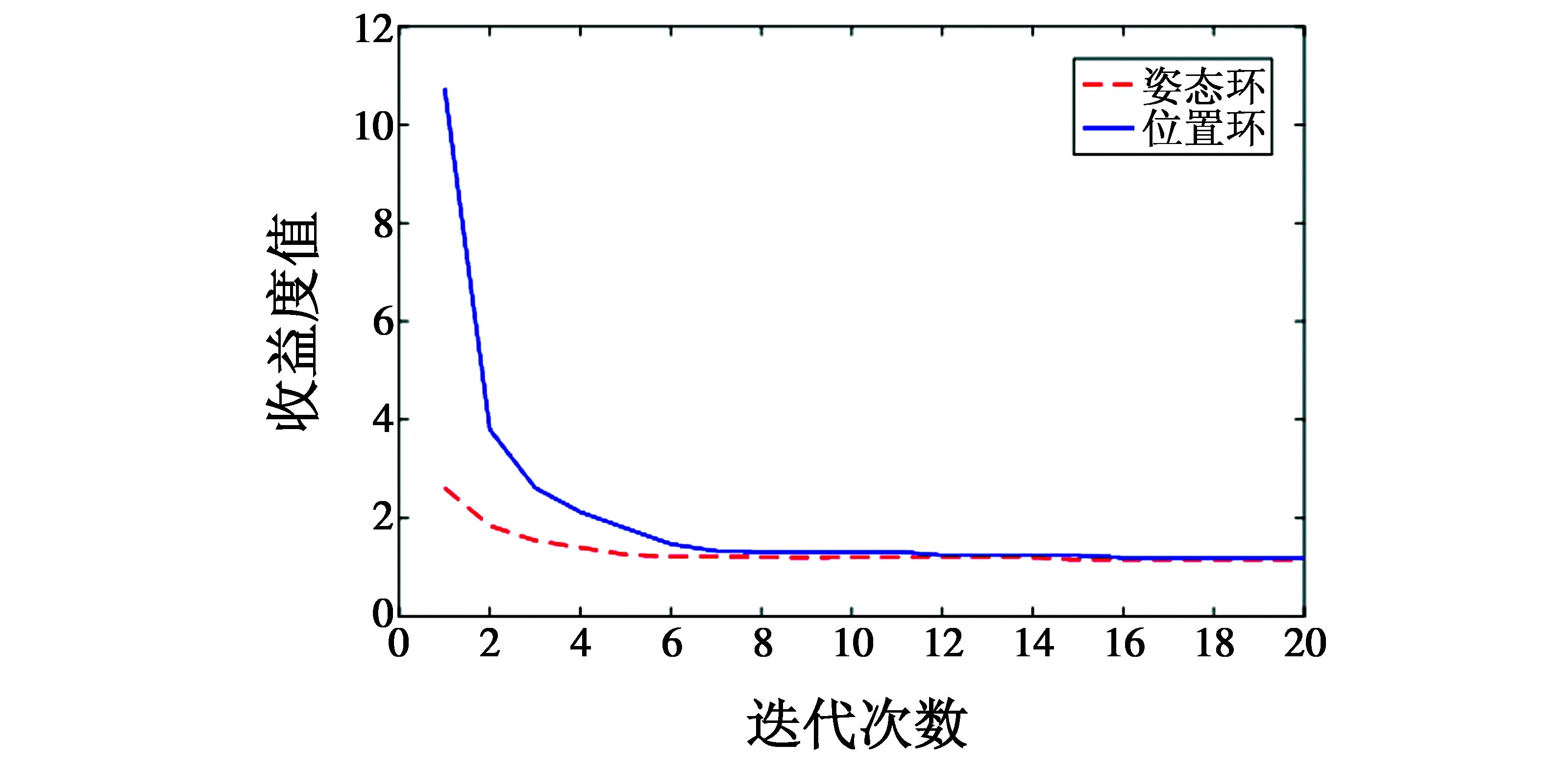
图7　迭代曲线Fig.7　Iterative curve

从图7可以看出，姿态环与位置环均在6代内就开始收敛，收敛速度很快。计算求得的姿态与位置的输出反馈增益分别为

Ko=

另外，图8给出了四旋翼角速度和线速度的响应，角速度和线速度也均能在2 s左右被镇定住。

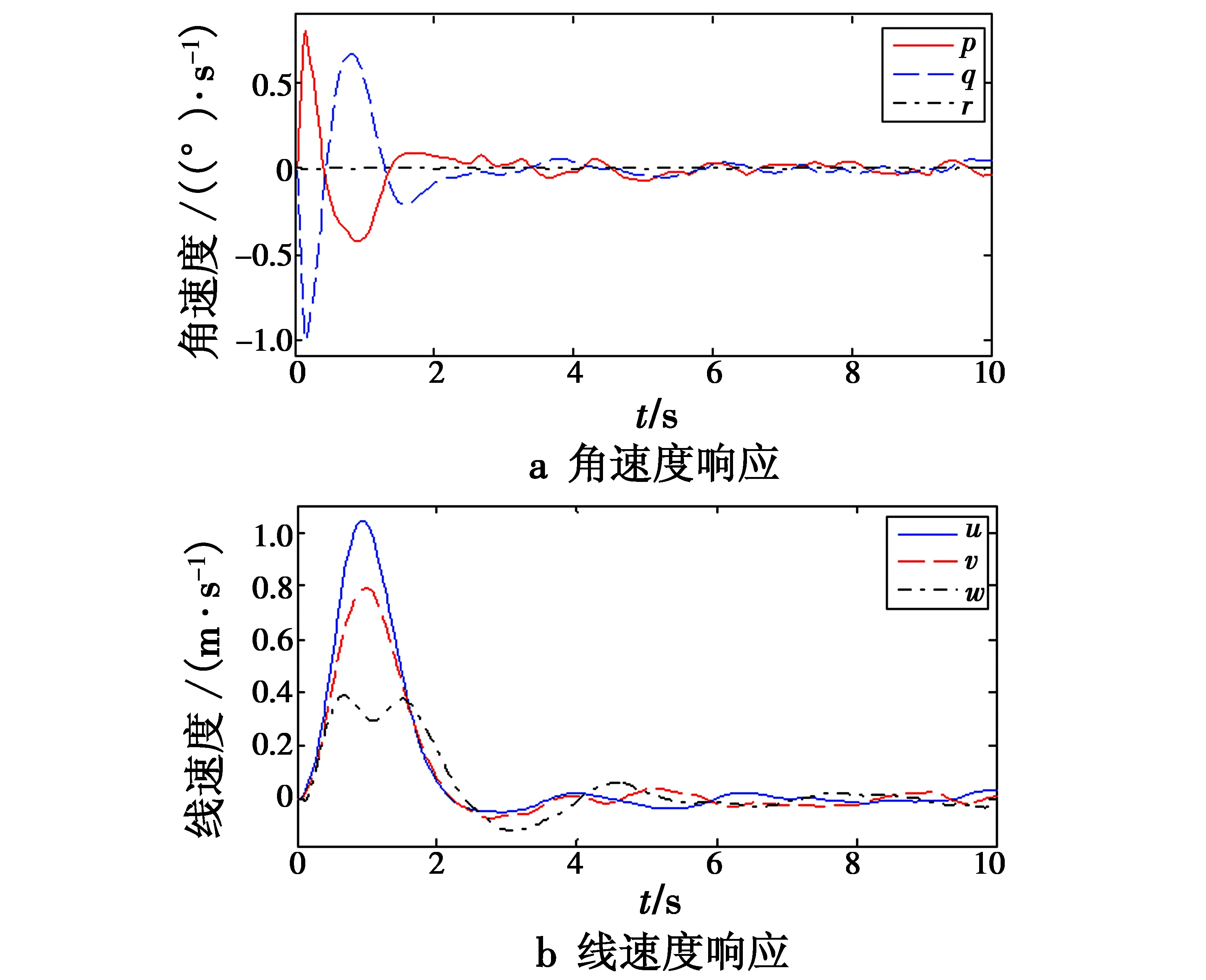
图8　速度的响应Fig.8　Response of velocities

为了测试本文所提控制算法在四旋翼轨迹跟踪方面的性能，让四旋翼跟踪“8”字型轨迹，跟踪过程持续40 s，悬停时间持续5 s。控制器的输出反馈增益使用上个算例中的优化结果，集总干扰的设置也与上个算例的条件相同。整个仿真结果如图9～图10所示。

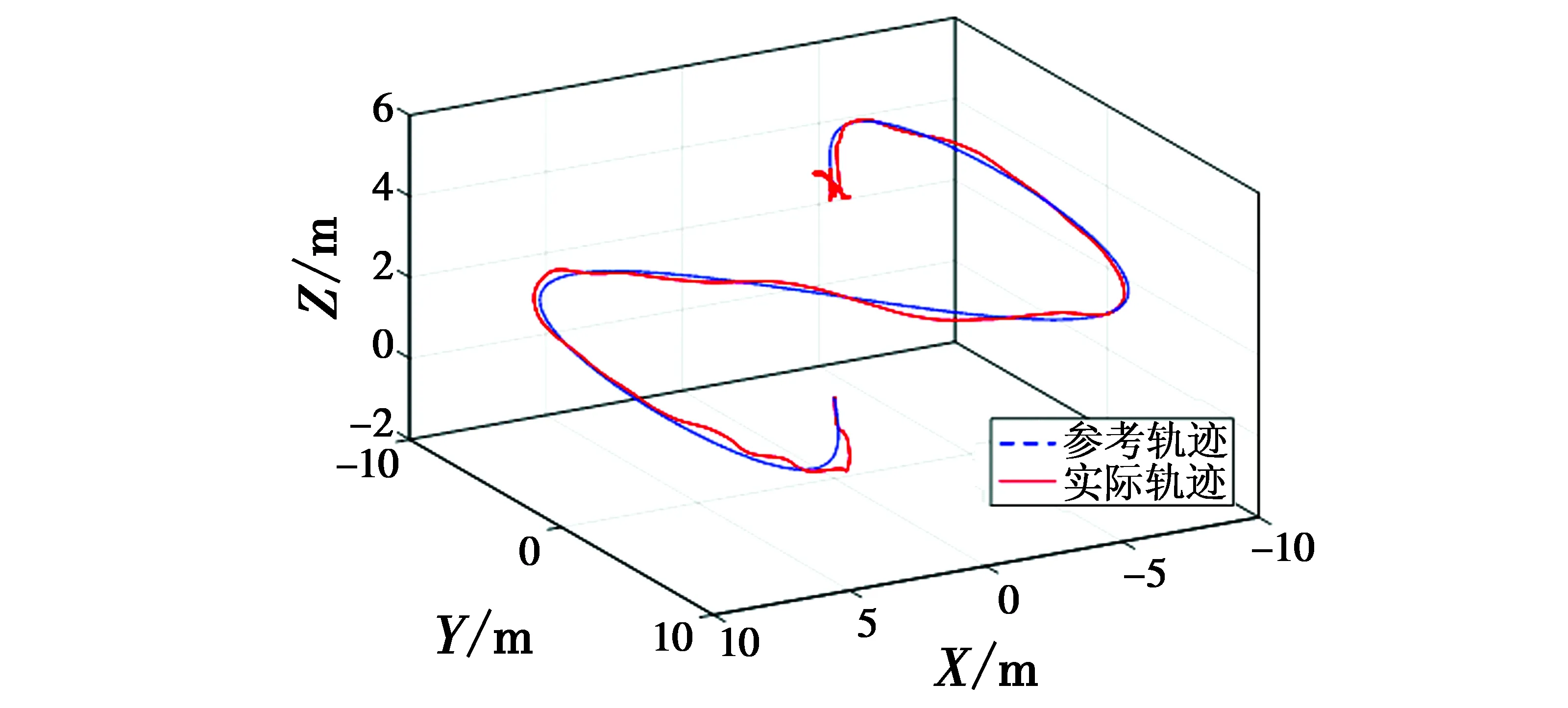
图9　三维跟踪曲线Fig.9　3D trajectory tracking curve

图10　XZ平面轨迹Fig.10　Trajectory in XZ plane

从图中可以看出，四旋翼在静态H∞输出反馈控制器的作用下基本能够跟踪上参考轨迹，对集总干扰也有一定的抑制；悬停时，位置的变化范围在Z轴方向上不超过±0.3 m，能够保持位置与位姿的稳定。这说明，本控制算法具有较强的鲁棒性。

4　结论

本文采用一种静态H∞输出反馈控制算法设计了集总干扰下四旋翼飞行器的姿态与位置控制器，可以获得如下结论：

1) 静态H∞输出反馈控制算法可利用输出反馈增益来补偿集总干扰，实现四旋翼系统的状态稳定控制，本文设计的控制算法响应速度快、鲁棒性高和抗干扰能力强；

2) CS算法能够在有限的迭代次数内获得最优的输出反馈增益矩阵，寻优能力强，收敛速度快；

3) 阶跃响应和轨迹跟踪仿真均验证了本文所提算法的有效性，今后将尝试将此控制算法写入控制硬件中，在实际飞行中测试控制算法的有效性。

[1]ABAUNZA H,CASTILLO P,VICTORINO A,et al.Dual quaternion modeling and control of a quad-rotor aerial manipulator[J].Journal of Intelligent & Robotic Systems：Theory & Applications,2017,88:267-283.

[2]SHIRZADEH M,ASL H J,AMIRKHANI A,et al.Vision-based control of a quadrotor utilizing artificial neural networks for tracking of moving targets[J].Engineering Applications of Artificial Intelligence,2017,58:34- 48.

[3]SALIH A L,MOGHAVVEMI M,MOHAMED H A F,et al.Modelling and PID controller design for a quadrotor unmanned air vehicle[C]//IEEE International Conference on Automation Quality and Testing Robotics(AQTR), IEEE,2010:1- 5.

[4]JAFARI H,ZAREH M,ROSHANIAN J,et al.An optimal guidance law applied to quadrotor using LQR method[J].Transactions of the Japan Society for Aeronautical and Space Sciences,2010,53(179):32-39.

[5]ALEXIS K,NIKOLAKOPOULOS G,TZES A.Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances[J].Control Engineering Practice,2011,19(10):1195-1207.

[6]CABECINHAS D,CUNHA R,SILVESTRE C.A nonlinear quadrotor trajectory tracking controller with disturbance rejection[J].Control Engineering Practice,2014,26:1-10.

[7]DONG W,GU G Y,ZHU X,et al.High-performance tra-jectory tracking control of a quadrotor with disturbance observer[J].Sensors and Actuators A:Physical,2014, 211:67-77.

[8]CHEN B M.Robust andH∞-control[M].New York:Springer,2000:62-102.

[9]GADEWADIKAR J,LEWIS F L,SUBBARAO K,et al.H-infinity static output-feedback control for rotorcraft[J].Journal of Intelligent and Robotic Systems,2009,54(4):629-646.

[10]李杰,齐晓慧,韩帅涛.基于自抗扰技术的四旋翼姿态解耦控制方法[J].电光与控制,2013,20(3):44-48.

[11]DOYLE J C,GLOVER K,KHARGONEKAR P P,et al.State-space solutions to standardH2andH∞control problems[J].IEEE Transactions on Automatic Control,1989,34(8):831-847.

[12]YANG X S,DEB S.Cuckoo search via Lévy flights[C]//Proceedings of World Congress on Nature & Biologically Inspired Computing,2009:210-214.

[13]马瑞,吴洪涛,丁力.基于人工蜂群算法的无人直升机LQG/LTR控制律优化设计[J].控制与决策,2016,31(12):2248-2254.

[14]王凡,贺兴时,王燕,等.基于CS算法的Markov模型及收敛性分析[J].计算机工程,2012,38(11):180-182.