基于变量泵控定量马达的风力发电系统建模仿真与试验研究

,,

(西安工程大学 机电工程学院,陕西 西安 710048)

风能取之不尽用之不竭，是一种清洁的可再生能源。随着化石燃料能源的日益枯竭，人们的环境保护意识逐渐加强，世界各国都正加紧开发和利用风能。世界风力发电的装机容量随之迅速增长，近年年均增长可达30%[1]。我国可开发的陆地和海洋风能资源大约分别为253 GW和750 GW。年平均风速达6 m/s以上的内陆地区约占全国总面积的1%，仅次于美国和俄罗斯，居世界第三位[2]。但目前我国风力发电装置还存在以下缺点:(1)风速不稳定问题；(2)以变频技术作为主流变速恒频发电技术带来的问题；(3)风力发电装置大部分部件的安装位置带来的问题[3]。变速恒频技术作为风力发电行业的主流技术，其电力电子变流器(安装在发电机和电网之间)的制作成本相对较高，这也是该技术的缺点所在。

随着液压技术的发展，泵控马达系统的应用技术越来越成熟，应用范围也越来越广泛[4-5]。按照液压泵和马达调速方式的不同，可分为以下三种类型：(1)变量泵-定量马达式调速系统；(2)定量泵-变量马达式调速系统；(3)变量泵-变量马达式调速系统。其中，变量泵-定量马达式调速系统通过调节变量机构的移距来改变泵的排量，进而实现对马达转速的控制。同时，变量泵作为液压系统的动力源,具有输入功率和输出功率相匹配、高效节能的特点,因此,被广泛应用于工程机械等领域[6]。此外，针对变量泵-定量马达液压容积调速，本文建立适当的数学建模，进而完成相应的优化研究和参考影响分析，为系统的设计和应用提供了理论依据，具有实际指导意义[7]。本文设计了一套变量泵-定量马达液压恒速系统，在该系统中，除风轮机和液压泵安装在塔上外，其余部分均安装在地面，以便维修。塔上安装的液压泵将吸收风轮机的风能转变为稳定的液压能，可为马达供油。同时，本文提出变量泵直接调速和比例调速阀旁路微调速的复合调速方法，使马达在1 500 r/min左右的转速下仍可稳定工作，发电机与马达同步转动，进而产出50 Hz的工频电。

1 变量泵控定量马达恒速系统原理

液压系统原理图如图1所示。液压系统主要由变量泵、定量马达、电磁溢流阀、比例调速阀及其它液压辅件组成。在主回路中，首先调节变量泵的变量机构来改变排量，将机械能转变为稳定的液压能后，再经过比例调速阀进行旁路调节。作为安全阀的溢流阀控制进入定量马达的油压，使马达进油口压力稳定。

由于系统流量大，故液压系统采用封闭式液压回路。在回路中，液压泵、液压马达以及实现不同功能的各种控制阀都可能存在泄漏，又因为液压泵的自吸能力较差，故本系统增设补油系统以便补充油量。

补油系统是一个小流量的恒压源，补油泵通过单向阀6向低压管道补油，用以补偿系统油液的泄露，同时单向阀6也可以防止低压回路压力过高时油液回流到补油系统。同时补油系统给闭式系统供油，还可以防止出现气穴现象和空气渗入系统，同时也能帮助系统散热。另外，蓄能器10可以消除或减弱系统的压力和流量的脉动给系统稳定性带来的影响。

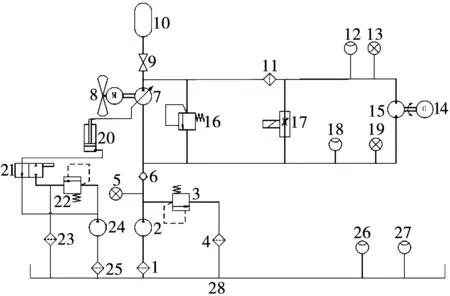
图1 液压系统原理图1-吸油滤油器；2-补油泵；3-电磁溢流阀；4-回油滤油器；5-压力表；6-单向阀；7-变量泵；8-风轮机；9-球阀；10-蓄能器；11-高压滤油器；12-压力传感器；13-压力表；14-发电机；15-定量马达；16-电磁溢流阀；17-比例调速阀；18-压力传感器；19-压力表；20-柱塞缸；21-两位四通阀；22-电池溢流阀；23-回油滤油器；24-变量机构泵；25-吸油滤油器；26-液位计；27-油温计；28-油箱。

2 变量泵的数学建模

变量泵的数学模型分为变量泵调节系统数学模型和变量泵数学模型。以四通阀控制液压缸位置作为变量泵变量系统的控制方法，变量泵的变量系统移距通过液压缸控制，从而实现对变量泵排量的控制。

(1)变量泵变排量系统的数学模型

根据变量泵变排量系统的特性，泵的斜盘为一个大惯量部件，所以将泵的变排量控制系统转化为一个一阶系统。泵的排量和控制电压的关系为

(1)

式中qp——泵的排量；

Uq——变量泵变排量机构的控制电压；

kx——变排量系统增益；

t——时间常数。

(2)变量泵的数学模型

液压马达转矩平衡方程

(2)

式中J——马达负载在马达轴上的转动惯量；

T1——负载力矩；

B——粘性阻尼系数。

流量连续性方程

(3)

式中QP——变量泵输出端流量；

qp，qm——泵和马达的排量；

cp，cm——泵和马达的泄漏系数；

k——油液体积弹性模量；

p——油腔压力；

v——油腔总容积。

建立系统数学模型,将上述(2)、(3)式进行拉氏变换，所得方框图和格式如下

qmp(s)=(Js+B)nm(s)+T1(s)

(4)

(5)

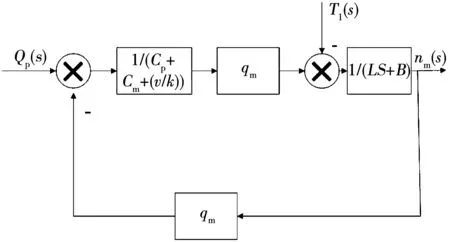
图2 系统方框图

3 系统动态分析

3.1 马达转速随负载的变换特性

系统的传递函数为

(6)

负号表示马达转速降低，负载转矩升高，

本次容积调速系统的阻尼系数为

(7)

本次容积调速系统的固有频率为

(8)

3.2 马达转速随泵的排量的变化特性

系统传递函数为

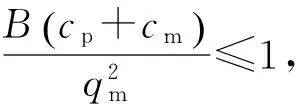
(9)

从上述传递函数看出，其均为振荡环节，且两个二阶系统特征方程中各项系数均为正值，由霍尔维茨判据式可知，运行始终稳定。

4 Matlab/Simulink仿真

风速变化的时空模型原则上可用以下四种典型成分来模拟：基本风VWB、阵风VWG、渐变风和噪声风。风在移动过程中，动能变化和势能变化同时存在。在一定的时间和窄间范围内，风速持续变化且随机。为展现系统在现实风场中的真实工作状况，同时捕捉风速的变化特征，较准确地描述风能随机性、间歇性的特点，本文从实际角度出发完成对风速的有效模拟[8-10]。

考虑到自然界风力的大小和方向的不可预测性，在仿真过程中，以10 kW风轮机为例，选取风速为3～6 m/s，对应泵的转速为20～40 r/min，考虑到变量泵与风轮机同步转动，故将渐变信号20～40 r/min作为仿真过程中液压泵的输入信号。

10kW风机风速/m·s-1输出功率/kW转速/r·min-120.11331.52043.12655.53368.240

图3 10 kW风轮机参数

利用MATLAB对液压系统进行动态仿真，进而完成相应分析,方便简单,在实际应用中有着重要的意义[11]。

本系统基于前馈的PID控制算法，通过变量机构主调，比例调速阀协助这一方式实现恒速。因发电机要求，马达的转速为1 500 r/min，根据定量马达规格参数和流量连续性方程，求出变量泵输出端流量QP，并作为设定值。在变量泵输出端检测出泵输出端流量，通过控制器比较，得出泵转速变化ΔQP，ΔQP经PID运算作用于变量泵的变量机构，对流入马达的流量进行粗调。马达转速基本稳定后，通过比例调速阀完成微调，从而使马达转速稳定在1 500 r/min。

变量泵-定量马达液压恒速系统的控制原理图如图4所示。

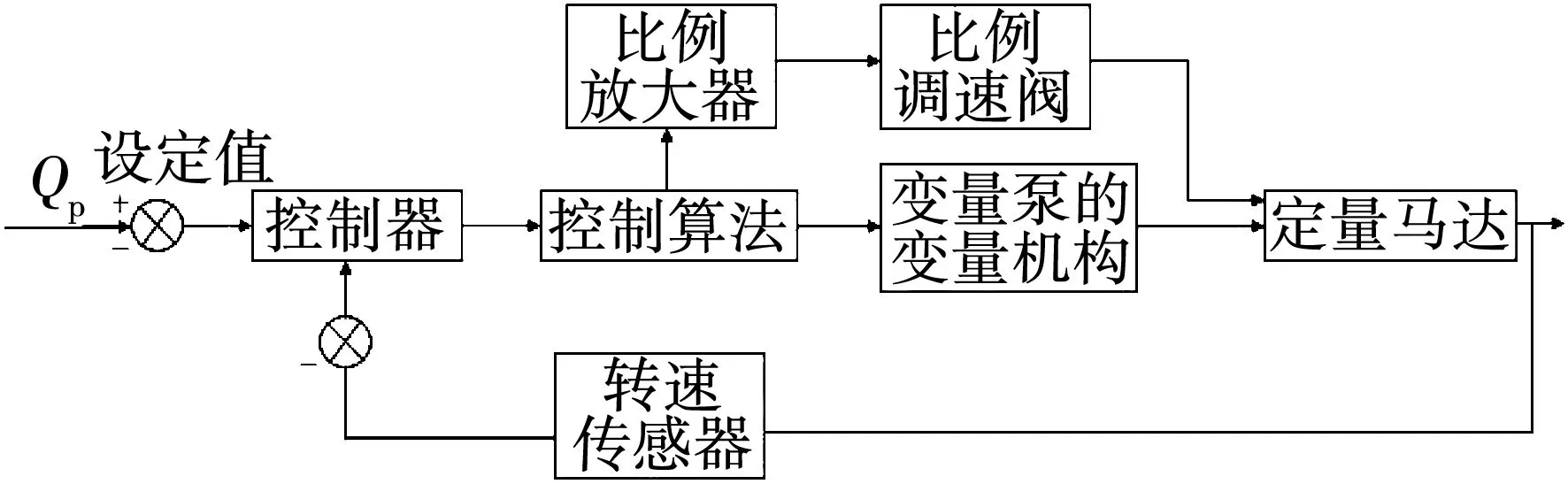
图4 控制系统原理图

普通比例-积分-微分(PID)控制器控制的算法结构简单，适用于线性控制系统[12]。如图5所示。

对系统进行仿真结果如图6所示。

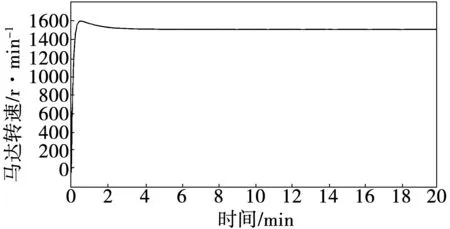
图6 仿真结果

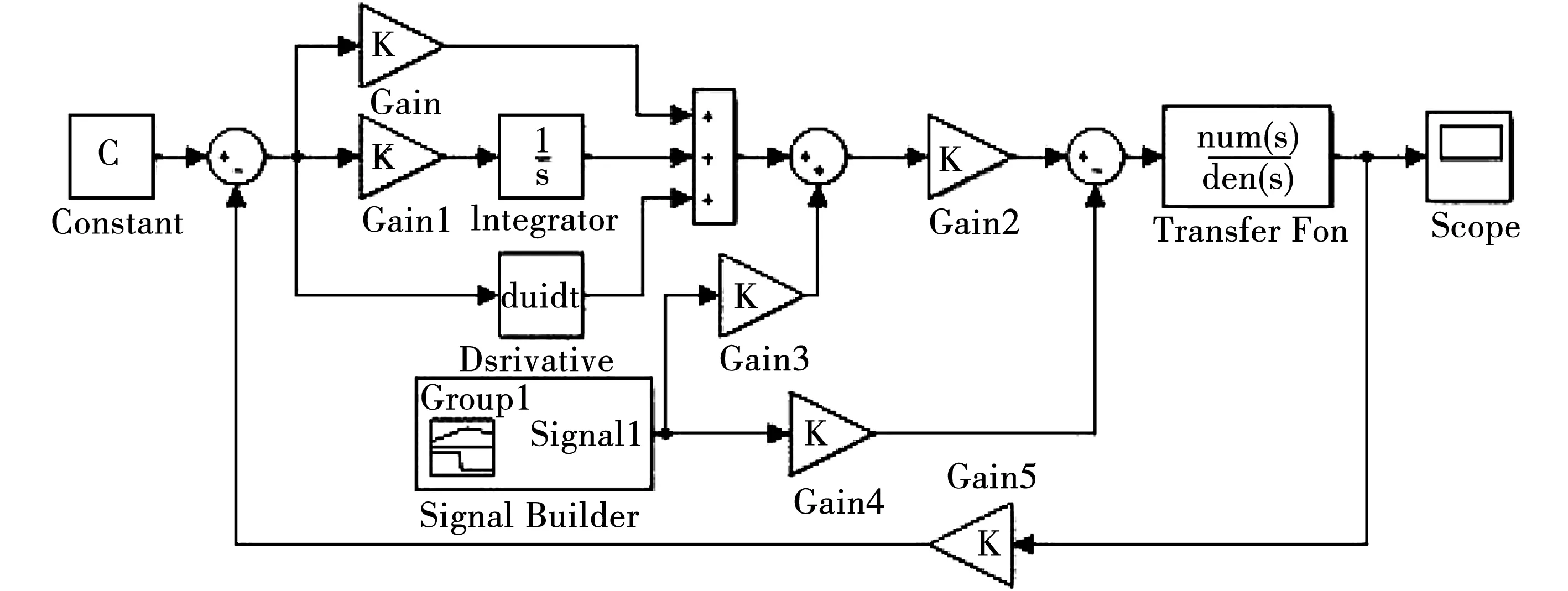
图5 系统仿真模型

由图6仿真结果得出，外界风速发生变化时，马达转速为1 500 r/min，波动范围在±15 r/min，可以稳定工作，满足发电机高品质发电要求。

5 系统运行试验

本系统以电机代替风轮机，利用变频器改变电机输入频率来模拟风速，变频器的输入频率在20～40 Hz之间循环变化。以10 kW风轮机为例，相当于风速在3～6 m/s。经二级减速器传动后，泵的转速范围在20～40 r/min。变频器频率变化曲线如图7所示。

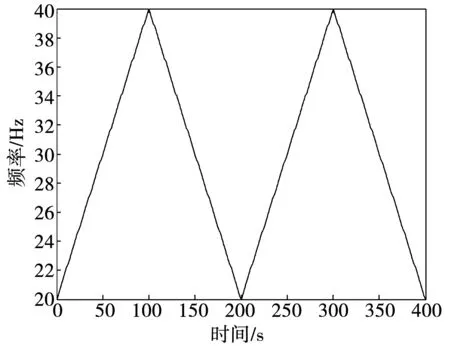
图7 变频器频率变化曲线

5.1 空载试验

调速阀流量的初始值为1 L/min，泵转速在20～40 r/min变化，空载时马达转速变化曲线如图8所示。

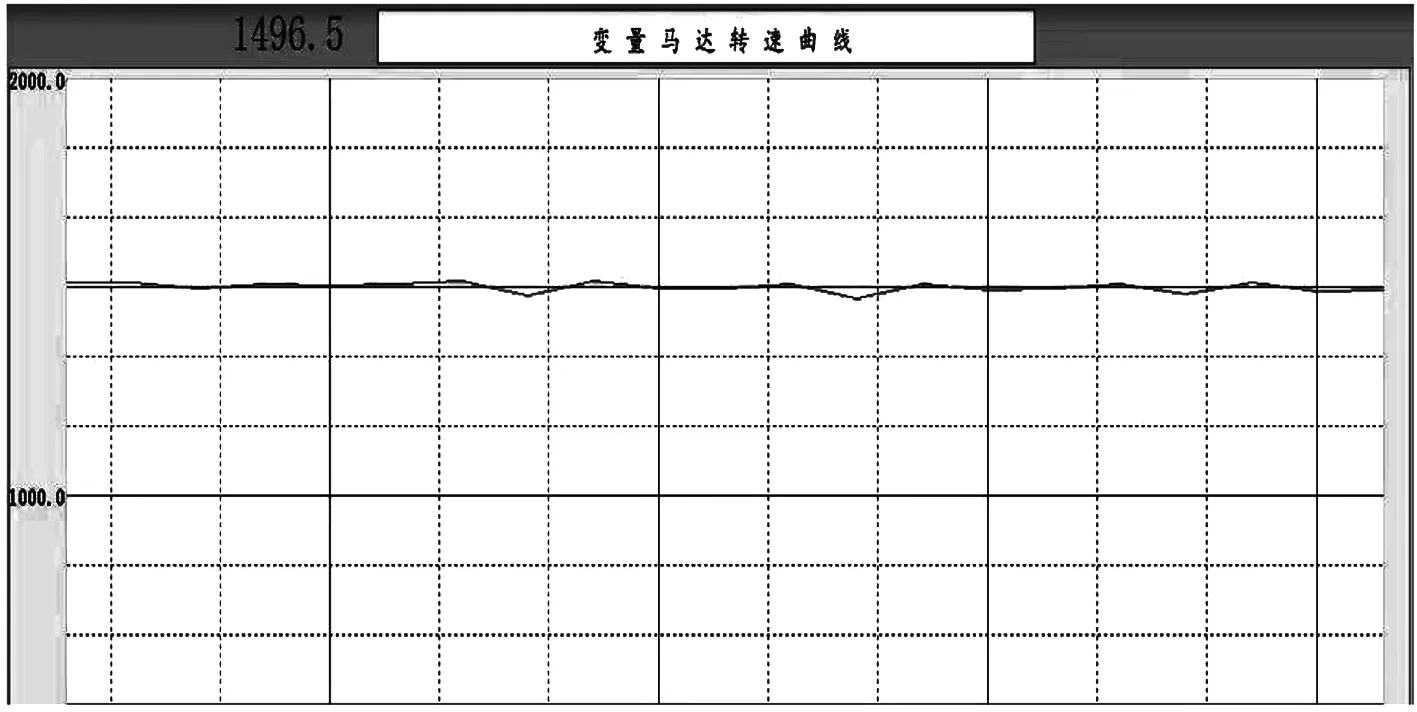
图8 空载时马达的转速变化曲线

由图8中马达转速反馈曲线和显示数据可知，系统运行稳定后，空载情况下马达转速基本稳定在1 500 r/min,波动范围在±15 r以内。

5.2 有载试验

泵转速在20～30 r/min变化时，系统加载10 kW，变量马达转速变化曲线如图9所示。

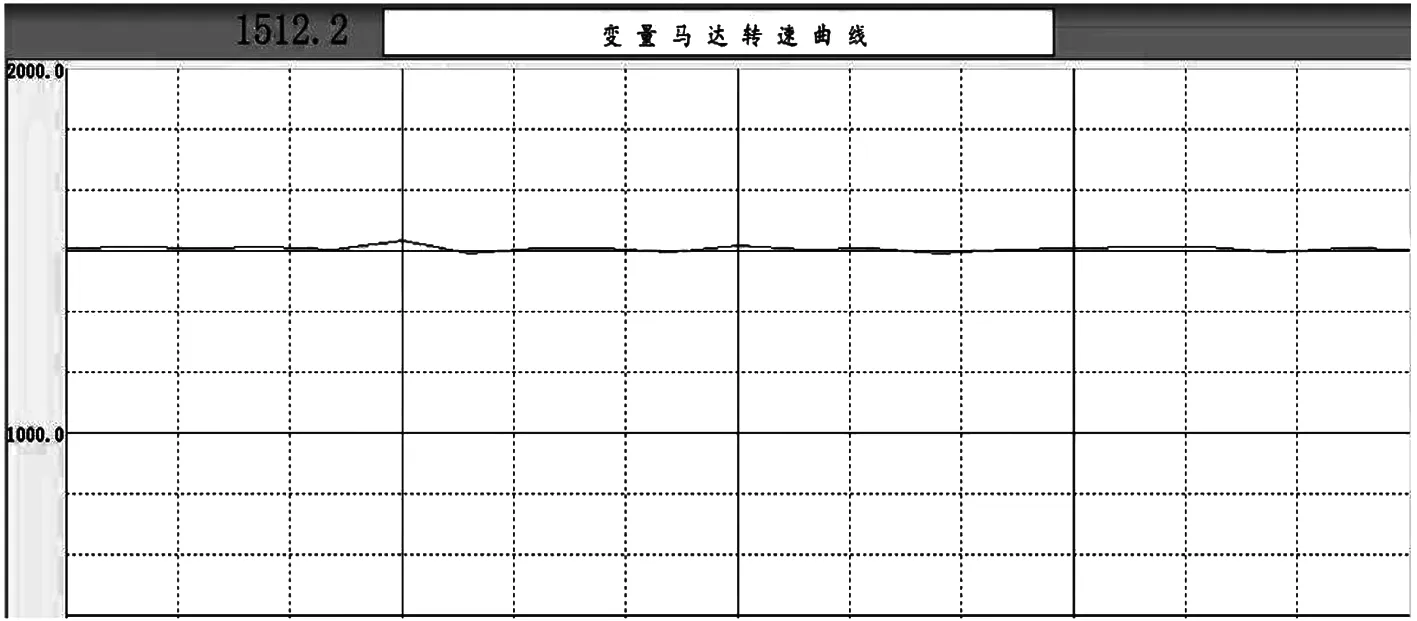
图9 加载时变量马达转速变化曲线

由图9中马达转速反馈曲线和显示数据可知，当加载10 kW发电机且系统运行稳定后，马达转速无波动下滑现象，基本稳定在1 500 r/min,波动范围在±15 r以内。

6 结束语

针对当今主流风力发电系统的不足，本文提出了一种新型变量泵控定量马达的风力发电系统。本系统的优点为：(1)除泵外，其它机构均在地面安装，既降低风力发电系统的重心，又增加了系统运行的稳定性，同时利于维护；(2)液压元器件成本相对低廉，弥补了现如今主流风力发电技术中，电力电子交流器价格昂贵的不足；(3)液压传动可以实现无极调速，并且油液可以吸收冲击，使其运行平稳。同时可以实现快速启动、快速制动。对于自动控制、远距离控制和过载保护等技术也易于实现。

系统采用的调速方法是主调变量泵变量机构，比例调速阀从旁协助的复合调速方法和PID控制算法对马达转速进行闭环控制，马达的转速作为反馈量，对系统建立数学模型，运用Matlab/Simulink进行了仿真研究，并对系统进行了运行试验。仿真和试验结果均表明，当风速变化时，马达的转速可以维持在1 500 r/min，波动范围在±15 r以内，相信对系统进一步的优化后，可以实现高品质发电。

[1]罗如意,林晔,钱野.世界风电产业发展综述[J].可再生能源,2010(2):14-17.

[2]刘波,贺志佳,金昊.风力发电现状与发展趋势[J].东北电力大学学报,2016,36(2):7-13.

[3]唐学用,叶航超,万会江,等.风电机组不同控制模式下SVC在改善电网电压质量中的应用[J].电网与清洁能源，2016,32(10):128-136.

[4]李帅.泵控马达闭式调速系统特性研究[D].杭州:浙江大学，2010:1-3.

[5]曾宗桢．大时滞大惯性变频泵控马达调速系统研究[J]．机床与液压，2007(35)：6.

[6]资新运,郭锋,王琛,等.电液比例变量泵控定量马达调速特性研究[J].工程机械,2007(7):45-48,1.

[7]邓克.变量泵-定量马达容积调速系统优化研究[J].液压气动与密封,2009(5):23-25.

[8]Jangamshetti SH,Rau VG.Optimum siting of wind turbine generators[J].Ieee Transactions on Energy Conversion,2001,16(1):8-13.

[9]许宝清，田德，吴骅，等.风速的Weibull分布参数确定方法研究[J].农业工程学报，2007(10)：31-34.

[10]Seguro JV,Lambert TW.Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,85(1):75-84.

[11]张红俊,李增玲.利用MATLAB实现变量泵定量马达调速系统的动态仿真[J].山西煤炭管理干部学院学报,2004(1):82-83,88.

[12]王建国,周燕飞.泵控马达系统的模糊PID控制与仿真[J].机械设计与制造工程,2015(11):44-47.