基于三角模糊和可变模糊集理论的地铁运营风险评价
2018-04-18潘科关守安
潘科,关守安
(1.大连交通大学 土木与安全工程学院,辽宁 大连 116028; 2.辽宁省安全科学研究院,辽宁 沈阳 110004)
0 引言
地铁运营风险评价在保障地铁车站及地铁列车的安全运营方面具有重要的作用.近年来,关于地铁运营风险评价体系及其方法的研究发展迅速.文献[1]分析了《地铁运营安全评价标准》在权重确定及评价方法方面的不足,尝试在地铁运营风险评价中引入变权理论和相对差异函数,以弥补个别指标因权重过小导致的评价结果失真问题.文献[2]针对地铁建设和运营特点建立了地铁运营安全评价的多级可拓评价模型.文献[3]为评估地铁安全运营水平,建立了基于DT 法的地铁设备设施动态分级模型.文献[4]基于Petri网络建立了地铁火灾应急响应模型.地铁运营风险评价体系的完备性、权重计算及评价方法的科学性是影响风险评价结果的主要因素,在现有的指标权重确定方法中,专家经验法和AHP法不同程度上且有一定的主观性,本文基于地铁运营风险的两大基本特征,即各指标对于地铁运营事故发生的可能性(RP)和后果的严重程度(RI)两方面考虑其影响,并采用三角模糊理论来解决风险影响因素的不确定性问题[5- 7],从而确定各风险指标的权重;考虑到可变模糊集理论解决模糊问题的合理性[8],论文提出了地铁运营风险评价的可变模糊评价方法,该方法能够科学合理地确定影响地铁运营风险各评价指标对各风险等级的相对隶属度,并且可以通过变化模型及其参数,合理地确定出地铁运营风险等级,提高其结果的可信度.
1 地铁运营风险评价体系的构建
基于系统安全的原理,影响系统安全的关键因素是“人-车(设备)-环境-管理”4个方面,对于地铁运营,将“人”的因素归纳为运营组织及管理层,针对《城市轨道交通技术规范》(GB 50490-2009)在“运营”、“限界”、“土建工程”、“车辆”、“机电设备”等方面的要求,并结合《地铁运营安全评价标准》(GB/T 50438-2007)及文献[4]的成果,建立并完善了地铁运营风险评价指标体系,如表1所示.

表1 地铁运营风险评价指标体系及取值
注:(1)表1中1级指标、2级指标的有关内容主要参考《城市轨道交通技术规范》(GB 50490-2009)地铁运营的有关要求,重点参考《地铁运营安全评价标准》(GB/T 50438-2007)的要求.(2)表1中的指标分值为《地铁运营安全评价标准》附录A-P中规定的该项总分值.考虑到计算的需要,将附录规定的该项总分值与实际取值转化为百分制,即第6列及第7列所示,如100(10)表示附录中该项总分值为10分,转变后为100分,85(8.5)表示该项实际取值为8.5分,将其转变成百分制后为85分.(3)对于《地铁运营安全评价标准》附录A-P中规定的有关定性定量指标分值,除依据该条款外,还应参照现行的地铁运营规范,如对于附录N土建评价表中“地下、高架结构与车站建筑”,其N1项要考虑《城市轨道交通技术规范》7.3.18条关于地铁换乘车站防火分区的有关要求,N11项要考虑进站口的安检系统.
2 三角模糊理论及其权重确定方法的构建
风险为事故发生的可能性及后果严重程度的综合度量,而不同的指标对于事故发生的可能性及后果严重程度是不一样的,且有一定的不确定性,因此科学的权重确定方法是考虑风险评价指标对事故发生后果及严重程度的影响,并采用数学方法来解决其赋值过程中的不确定问题,而三角模糊理论可以有效解决这一问题.
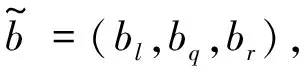
(1)
式中,在地铁运营风险评价中,bl为指标赋值区间中的最小值;br为指标赋值区间中的最大值;bq为指标赋值区间中的最可能值.
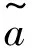
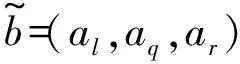
(2)
式中,al,ar,aq的意义同bl,br,bq.
根据地铁运营风险影响因素及三角模糊理论,其权重确定步骤如下.
(1)定义风险因素(RF)
根据地铁运营的有关特点及风险的两大基本特征,即事故发生的可能性(RP)以及后果的严重程度(RI).依据文献[5]及文献[6],表2、表3给出RP和RI模糊数的定义,包括其相应的语言变量、地铁运营中关于可能性及后果严重程度的参考值和对应的三角模糊数.

表2 事故发生的可能性(RP)描述
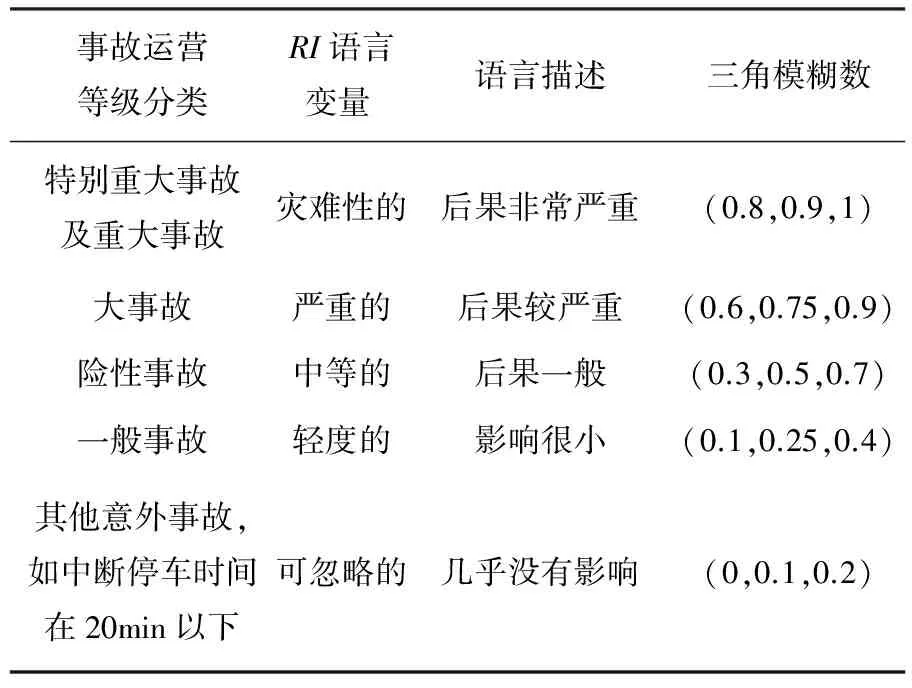
表3 后果的严重程度(RI)描述
注:事故运营等级分类参照《地铁运营安全评价标准》(GB/T 50438-2007)第19.2.1条.
(2)确定风险因素(RF)
按照风险的定义,得出风险层次结构的底层指标的风险因素RF的计算公式如下:
RF=RP⊗RI
(3)
(3)解模糊化过程
使用重心解模糊法[7],其具体转化公式如下:
(4)
(4)归一化处理
1级指标和2级指标的权重ωi和ωij可由式(8)求得:

(5)
3 地铁运营风险评价的可变模糊评价模型
设地铁运营风险评价因素集为{y1,y2,…,yn},y1,y2,…,yn为1级指标,每个1级指标有m个级指标,则有待评价对象的特征值矩阵为X=(xij).xij的值主要由被评价对象的实际情况与《地铁运营安全评价标准》附录A-P中规定的有关定性定量指标分值取得,如对于安全管理评价中的“事故应急救援体系(20分)”包括“应急救援机构(3)”、“预案制定情况(4分)”、“预案管理(1分)”、“应急设备及人员配备情况及维护体系(6分)”、“事故应急培训及应急演练(4分)”、“当年紧急事故处置(2分)”五项内容,而每项内容又根据其分项组成进行打分,其分值结果相对符合实际情况.
3.1 相对差异函数模型及其指标特征值的模糊化
3.1.1相对隶属函数及相对差异函数
设U为论域,u为U的任意元素,元素u的一对对立模糊概念,或u对立的两种基本模糊属性:A和Ac.分别赋予A和Ac处于共维差异中介过渡的两个端点以1、0与0、1的区间数.分别在1到0和0到1的数轴上构成一对[1,0]与[0,1]闭区间数的连续统.对于U中的元素u,都在该连续统的任一点上指定了一对数fA和fAc,将fA和fAc分别称为u对A和Ac的相对隶属度.定义如下式的映射[11]
μA(μ):u|→fA∈[0,1]
μAc(μ):u|→fAc∈[0,1]
(6)
μA(u)和μAc(u)分别为u对A、Ac的相对隶属函数.
设fd=fA-fAc,fd为u对A的相对差异度.映射
D(u):u|→fd∈[-1,1]
(7)
D(u)为u对A的相对差异函数.
3.1.2利用相对差异函数确定相对隶属度的方法
对于地铁运营风险评价因素集为{y1,y2,…,yn},假设每个因素的风险论域可划分为k个等级.根据标准规范或者评价目的,可将第i个1级指标中第j个因素的第h个风险等级的标准值区间设定为[aijh,bijh],该因素第h个风险等级的上下界区间为[cijh,dijh].而mijh为区间中D(u)=1的点值,即该因素在第h个风险等级的最可能取值.xij为论域上任意点的量值.
根据可变模糊集理论,地铁运营风险评价的可变模糊集合的吸引域Iab、范围域Icd和完全隶属于矩阵Iab的点值矩阵M分别如式(8)~(10)所示:
Iab=([aijh,bijh])
(8)
Icd=([cijh,dijh])
(9)
M=(mijh)
(10)
式中,M的第i行、第h列元素为mijh.根据h确定mijh:当h=1时mi1=ai1;当h=k时mik=bik;当1 若xij落在mijh值的左侧,xij相对于风险等级h的隶属函数为: (11) 反之则: (12) 根据式(11)、(12),确定评价对象特征值矩阵X对各个风险等级的相对隶属度矩阵,如式(13)所示. iU=(μAh(xij)) (13) 根据文献[8],地铁运营风险的模糊可变评价模型如式(14)所示: (14) 将式(14)计算结果归一化后得到第i个1级指标的隶属度矩阵iUh: iUh=(iuh) (15) 式中,iuh为第i个1级指标归一化后的相对于风险等级h(h=1,2,…,k)的隶属度;iUh的第i行、第h列元素为iuh. 应用级别特征值公式,1级指标i的级别特征值为hi,令H=(h1,h2,…,hn),则: H=(1,2,…,k)·jUh (16) 式中,k表示对应的风险等级;“·”表示矩阵相乘. 根据H对待评价对象进行综合评价得到其级别特征值: h0=(ω1,ω2,…ωn)·HT (17) 式中,ωi为第i个1级指标的权重. 1)根据表2、表3确定各指标的RP和RI评价值,利用式(3)、(4)确定RF值及RFT值,确定利用式(5)确定1级指标及2级指标的权重,分别如表1的第3,5列所示,如1级指标的权重确定过程如表4所示. 表4 1级指标RP和RI评价值及其权重确定过程 2)根据该地铁运营的实际情况,采用集值统计法获得各指标分值,如表2的第6列所示.结合评价对象,参考文献[8]及《地铁运营安全评价标准》中关于地铁运营风险及相关风险级别的分级标准,确定风险等级论域为V={不可接受,基本可接受需改进,可接受,可忽略},以数值1,2,3和4分别表示这4个风险等级.在该体系中,取所有指标的风险分值区间均一致,则风险评价的可变模糊集合的吸引域为Iab=[0,60)[60,80)[80,90)[90,100]),范围域为Icd=([0,80)[0,90)[60,100)[80,100]).根据指标的吸引域区间及相对隶属函数对于点值矩阵的要求,确定各指标4个等级的点值矩阵为(mi1,mi2,mi3,mi4)=(0,65,85,100). 根据以上的各参数取值,对每个指标值应用式(11)~(13)计算,并将结果归一化,可得每个指标的相对隶属度矩阵,如表1第8~11列.根据2级指标的权重及相对隶属度,应用式(14)~(16)可求得各1级指标的级别特征值,如表5第2~5行所示;1级指标的权重及级别特征值利用式(17)可得到目标层的级别特征值,如表5第6行所示.由表5可知,4种模型下的评价结果的离差只有0.062,评价结果均为3级(可接受),偏向于2级(基本可接受需改进). 表5 1级指标4组模型参数的评价结果表 将该地铁运营线路经基础分值评价法与可变模糊评价所得的两种评价结果进行对比,如表6. 表6 2种评价结果的对比 从两种评价方法的评价结果来看,其总体风险水平都偏向“可接受”,但对于可变模糊评价方法,还能得出期1级指标所处于的风险水平,如对于“安全管理评价”1级指标,其风险处于“需改进”状态,因此可以通过完善其所属风险较高的2级指标来改善其风险水平,如对于“事故应急预案及应急体系”,该地铁运营公司虽然对应急救援预案进行了编制,但预案的演练方式较为单一,并且演练缺乏相应的计划、总结及评估.因此建议该地铁运营公司应定期组织多种形式的应急演练,并对其内容进行总结、评估,根据地铁运营发展现状对预案进行维护更新. (1)根据地铁运营风险评价体系中各指标对于风险发生的可能性及后果严重程度来确定指标权重的思想是合理性的,采用的三角模糊理论在处理地铁运营风险评价的不确定性问题是可行的; (2)应用可变模糊集理论,用相对差异函数来确定地铁运营风险隶属度向量是可行的.可变模糊评价模型不仅权重向量可变,且模型参数α、p可变,该方法突破传统方法只用一种模型对评价对象进行评价的作法,可以提高评价的可靠性,而从计算结果可以看出通过变换模型参数得到的级别特征值较稳定. 参考文献: [1]潘科,石剑云. 变权和相对差异函数在地铁运营安全评价中的应用[J].铁道学报,2009,31(3):20- 25. [2]潘科,王洪德,石剑云. 多级可拓评价方法在地铁运营安全评价中的应用[J].铁道学报,2011,33(5):14- 19. [3]胥旋,钟茂华,史聪灵,等. 基于动态分级法的地铁设备设施风险评价研究[J]. 2013,23(7):61- 66. [4]LI QIMING,DENG YONGLIANG,LIU CONG,et al.Modeling and analysis of subway fire emergency response:An empirical study [J].Safety Science,2016,84:171- 180. [5]范英,李辰,晋民杰,等.三角模糊数和层次分析法在风险评价中的应用研究[J].2014,24(7):70- 74. [6]WAN SHUPING,WANG FENG,LIN LIPIAN,et al.Some new generalized aggregation operators for triangular intuitionistic fuzzy numbers and application to multi-attribute group decision making[J].Computers & Industrial Engineering,2016,93:286- 301. [7]NIETO-MOROTE A,RUZ- VILA F.A fuzzy approach to construction project risk assessment[J].International Journal of Project Managerment,2011,29(2):220- 231. [8]PAN KE,JIANG QIU-YUAN,YAN SHAN-YU.Variable Fuzzy Assessment Method and Its Application in the Evaluation of Chemical Industry Park Emergency Response Capability[C]//Progress in safety science and technology,Beijing:Science Press,2010:171- 176.3.2 基于相对隶属函数的模糊可变评价模型
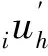
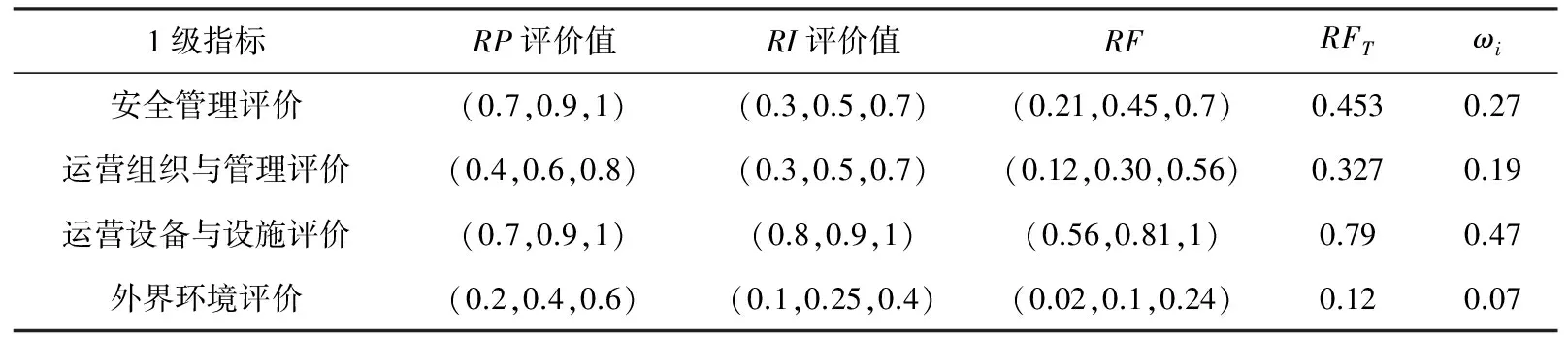
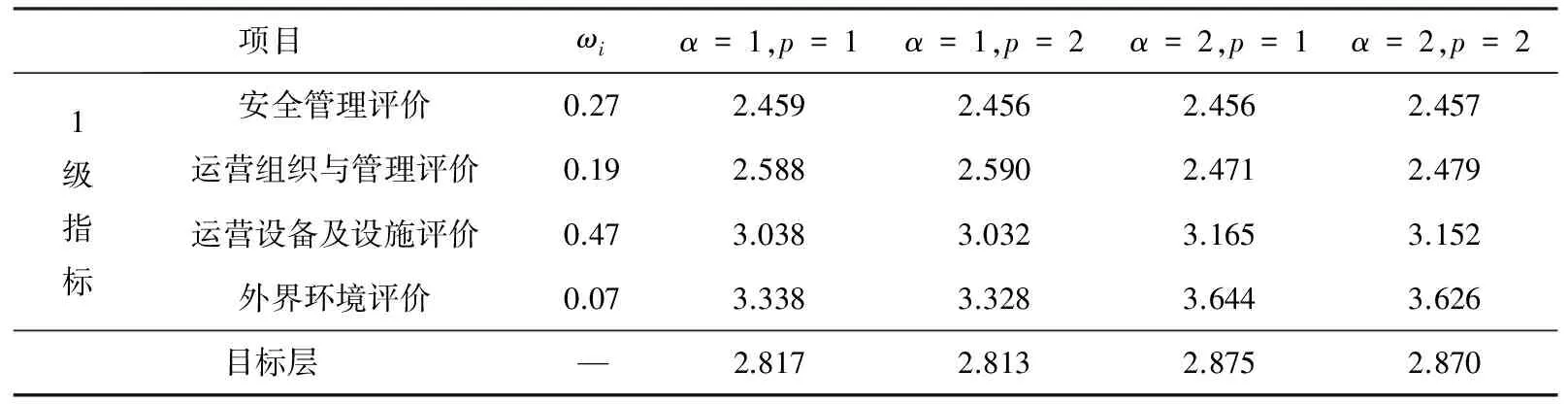
4 实例分析

5 结论
