上游停靠站公交溢出影响下交叉口公交优先配时优化
2018-04-18郑锐李锐薛鑫郑长江
郑锐,李锐,薛鑫, 郑长江
(1.河海大学 土木与交通学院,江苏 南京 210098;2.江苏省交通基础技术工程研究中心,江苏 南京 210098)*
0 引言
目前国内城市交通问题日渐严重,其中交叉口作为城市道路的节点,是车辆延误产生的主要因素.为减缓道路车辆拥堵问题,目前国内外普遍采用优先发展公共交通的措施.而公交停靠站作为道路上的又一重要节点,站点公交车停靠必然引起同行的社会车运行状态发生改变.对于公交在站点停靠的实际情况中,站外溢出现象较为普遍.因此,需要从公交停靠站溢出影响的角度,研究交叉口公交信号优先配时方法,提高公交车辆服务水平.
针对公交服务时间的研究,Diab等[1]分析实施组合策略对公交时间等参数的影响,以提高公交服务运行效率和乘客满意度.Bian等[2]提出复合泊松服务时间估算模型,用来获得各公交线路服务时间的估计值.左忠义[3]通过计算机模型和公交到站时间预测算法,向乘客手机客户端发送公交到站信息.针对交叉口附近设有公交站点的情况,Gu等[4-5]分析交叉口上下游公交站所造成的车辆和乘客的延迟与距离的关系,作为公交站点位置设置的参考.Li[6]针对下游的公交停靠站,建立交叉口公交信号优先模型,以减少下游公交站点乘客等待延误.关于公交信号优先方面,Ma[7]和Yang[8]利用实时信号状态和公交到达时刻控制车速并预测到达交叉口的时间,为公交提供优先通行权,降低公交时刻表偏差.Christofa[9]提出基于乘客延误最小的实时信号控制系统,基于公交运行准点性考虑,对模型中运行时间增加一个加权因子加以修正.Qu等[10]基于最佳实时交通优先控制,建立单点公交优先实时控制模型.Bhouri等[11]提出多式联运管制策略,调整交叉口信号灯以调节交叉口交通运行状态,提高公交服务水平.金勇等[12]以交叉口通行能力最大和车辆平均延误最小为目标,提出一种信号配时优化模型.关于设置公交专用车道的研究,He[13]利用在交叉口上游设置公交专用车道为公交提供优先级.Vikovych[14]研究交叉口公交专用进口道的设置规范,给出公交专用进口道的设置条件.Yao等[15]提出双模式可降解道路网络中公交专用道的评价方法,将双模式用户平衡模型与乘客风险行为结合,提出风险评估机制.Long[16]提出公交信号优先级与空间优先级相结合的控制理念,研究TSP与RSP(道路空间优先)综合作用的影响效果.
在现有交叉口信号配时研究中,常忽略公交站点的影响作用.对于上游附近的停靠站,公交车先进站再驶出通过交叉口,故公交停靠会产生一定相位绿灯损失时间,亦会造成本车道后续社会车辆被迫停车,从而降低了进口道通行能力,相比于下游站点对交叉口具有更大的影响.故本文以交叉口和上游停靠站作为研究对象,提出一种考虑公交站点车辆溢出影响的、基于乘客流量的公交信号优先配时方法.
1 公交停靠站车辆溢出影响分析
1.1 站点溢出模型建立
在实际道路交通中,公交车辆在站点停靠有多种可能性,车辆溢出等待时间用tw表示,基于本文所探讨的情况,将公交停靠大致分为以下两类:
(1)到达站点的公交车数目小于等于站点泊位数,公交车直接进站无溢出,站外的等候时间tw=0;
(2)到达站点的公交车数目大于站点泊位数,超出泊位数的公交车需站外排队等候再进站上下客,此时产生溢出,站外等候时间tw≠0.
1.1.1溢出排队原理
本文研究仅有一个停车位的站点,也称为单泊位站点,到达的公交车遵循先到先停,溢出车辆在站外排队依次进站的规律,公交进站溢出现象如图1所示.
图1(a)表示溢出队列中第一辆公交车排队过程,由于泊位被前一公交车辆占据,所以该公交车被迫减速停车.开始停车时刻存在两种可能:①代表与前车同时到达站点,紧接前车停车;②代表在前车停靠一段时间但出站之前到站,之后开始被迫停车.第一种情况公交排队消耗时间最多;第二种情况公交排队时间介于最大值与最小值之间,主要取决于该车到站时刻.
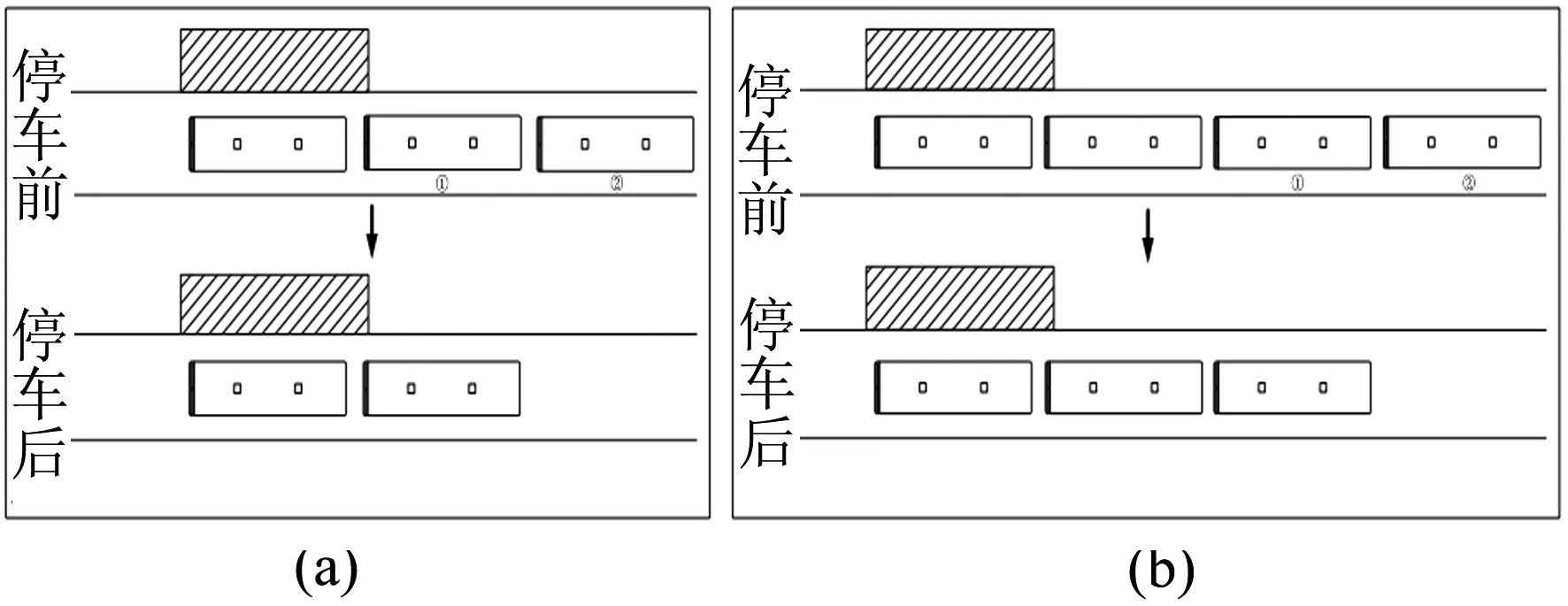
图1 公交排队原理示意图
图1(b)表示溢出队列中第二辆公交车排队过程,由于前面有车辆停靠,所以被迫减速停车.开始停车时刻也存在两种可能:①代表与第一辆排队公交同时到达站点,紧接其停车;②代表在第一辆排队公交停靠一段时间但启动之前到站,之后开始被迫停车.第一种情况公交排队消耗时间最多;第二种情况公交排队时间介于最大值与最小值之间,主要取决于该车到站时刻.
利用上述原理,即可分析出队列中每辆公交车排队过程.
1.1.2溢出等待时间模型
根据1.1.1的分析可知,公交到站时刻具有随机性,车辆可能同时到达站点,也可能存在一定的时间差,也即需要考虑车头时距的问题.针对许秀华[17]“公交车在公交停靠站的停靠时间研究”一文中将车辆视为同时刻到达的理论提出改进.
对于溢出的公交车辆而言,随着到达时刻的不同,需站外等待的时间也有所不同.因此,等待时间不仅受前车服务时间的影响,还应考虑到时间差的因素.所以,图1(a)所示排队的第一辆公交车等待延误为站内车辆剩余服务时间,图1(b)所示排队的第二辆公交车等待延误为第一辆公交车剩余等待时间与站内服务时间之和.以此类推,后续排队车辆等待时间为前一车辆剩余等待时间与队列前方所有车辆站内服务时间之和,表达式为:
(1)
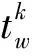
1.2 站点溢出对交叉口通行能力修正
本文以占用外侧直右混行车道、直线式单泊位公交站作为研究类型,借鉴葛宏伟[18]的理论,公交停靠溢出过程如图2所示.
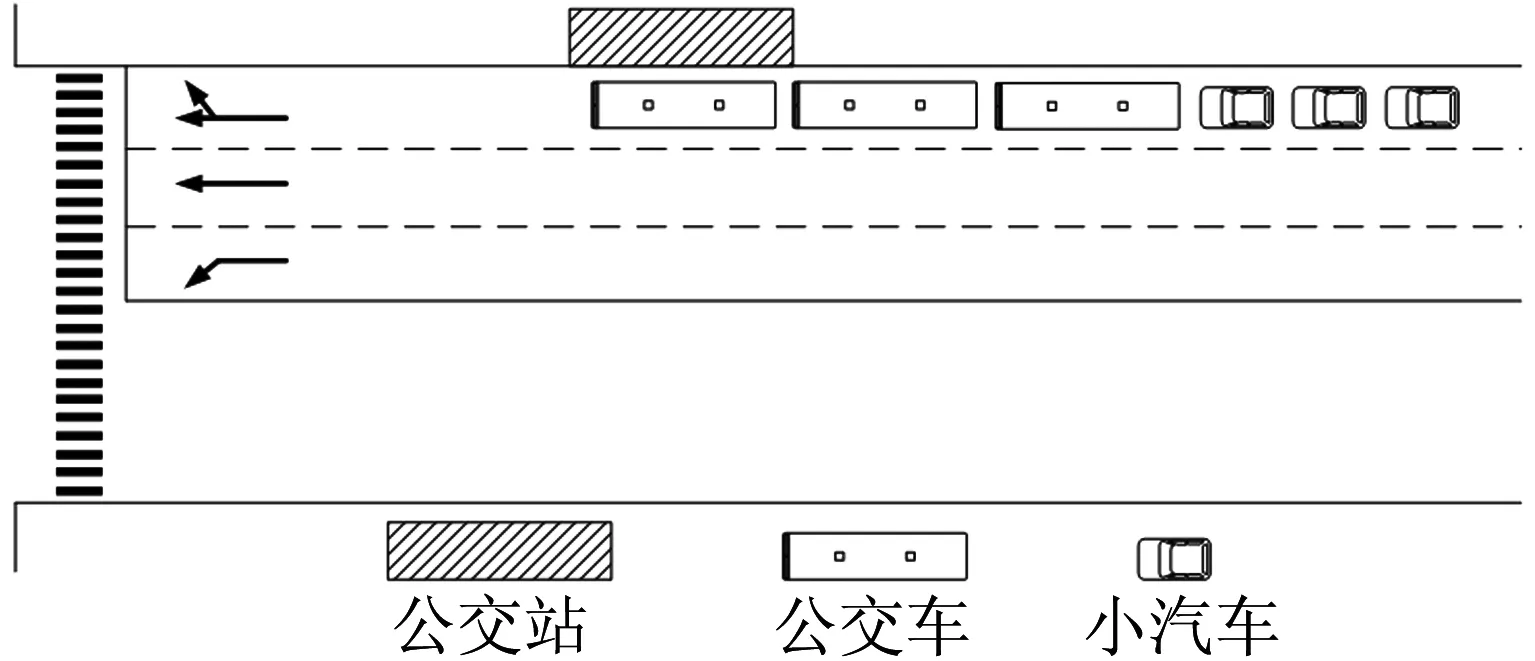
图2 公交溢出产生影响示意图
本文只考虑因公交停靠产生的影响,而暂不考虑后续社会车辆换道对道路交通的负面作用.综合站点有无公交溢出,得到直右混行进口道附近站点每辆公交停靠产生的进口道通行能力损失模型为:
(1)当时:0≤tL≤r-ts-tw时:
(2)
(2)当时:r-ts-tw≤tL (3) (3)当tL>r时: (4) 式中:Cmn为每次公交停靠造成的通行能力损失量;L为交叉口与停靠站的间距;tL为公交站点被交叉口车辆堵塞的时间;s为公交停靠占用车道的饱和流量;C为信号周期;f为公交车辆到达交叉口的时间服从0~C的均匀分布密度函数;r为公交相位红灯时长,ts公交站内服务时间;tw为公交站外等待时间. 那么,单位小时内公交停靠造成的通行能力损失表达式为: (5) 式中:M为经过该站点的所有公交线路;N为某一公交线路的所有公交车. 公交停靠站处乘客行程时间包括站内乘客出行时间和车内原有乘客延误时间.其中,站内乘客出行时间包括等待时间和上下车时间.乘客到达站点时间关系如图3所示,两区域分别代表同线路连续到达的公交车乘客出行情况,由关系图可得每辆公交车乘客行程时间为: (6) 图3 公交站乘客到达-离开时间关系图 公交车进站停靠会对车内原有乘客造成延误,当考虑到公交进站有溢出时,因溢出造成公交站外停车等候,进而增加了车上乘客的延误.考虑是否有公交溢出情况,得到车内乘客延误时间为: (7) 式中:Pb为公交车平均载客数. 进一步得到公交停靠站公交乘客总行程时间模型为: (8) 在公交溢出影响研究基础上,针对只有一个进口道设置停靠站的交叉口进行公交信号配时优化.以交叉口和停靠站乘客总延误最小为控制目标,以保障其余相位车辆能够正常通行为约束条件,建立信号配时优化模型,对公交优先相位的绿灯时间进行调整. 目标函数为: (9) 其中,社会车平均延误采用HCM2000模型,社会车与公交车换算系数比为1∶2,故所有车辆平均延误表达式为: (10) 式中:Pf为车均延误修正系数,推荐值为1;T为分析期(h),推荐值为0.25;K为取决于控制设置的修正系数,推荐值为0.4;I为上游车辆过滤修正系数,推荐值为1;Cij为站点溢出情况下i相位j进口道的通行能力;d0为初始排队延误,推荐值为0. 公交相位绿灯时间优化模型为: gb=gb0+gx (11) 非公交相位绿灯时间优化模型为: (12) 式中:gb为优化后公交优先相位绿灯时长;gb0为优化前公交优先相位绿灯时长;gx为公交相位绿灯优化时长;gj为优化后相位的绿灯时长;gj0为优化前相位j的绿灯时长. 选取南京市珠江路/丹凤街交叉口为例,该交叉口为平面十字型交叉口,东进口道附近设置有公交停靠站-莲花桥站,其余进口道无停靠站存在.由于站点泊位数为1,所以公交进站会出现溢出现象.交叉口信号控制为四相位(南北直行为第一相位,南北左转为第二相位,东西直行为第三相位,东西左转为第四相位),右转不受信号控制,东进口禁止左转,周期C=131 s,黄灯时间分别为2、2、2、3 s,交叉口信号控制如图4所示. 对交叉口进行工作日晚高峰交通量调查,调查时间为晚高峰16∶30~17∶30,流量数据如表1所示. 图4 交叉口信号配时图 表1 晚高峰交叉口交通流量表 pcu/h 针对莲花桥站进行工作日晚高峰乘客出行调查,站点公交线路共有5路,分别是#6、 #65、 #91、#47和#160,1 h内观测得到共有60辆公交车经过该站点.分析公交车进站有无溢出等情况,并根据许秀华[17]文献中公交站内停靠时间公式以及本文溢出公交站外等待时间模型(1)进行计算,得到具体数据如表2所示. 表2 莲花桥站公交到达情况调查表 s 图5 优化前进口道通行能力折减量统计图 利用站点调查数据, 根据1.2中通行能力损失公式(4)计算得到通行能力折减量如图5所示,1 h内进口道通行能力折减总量为158 pcu/h. 根据停车时间、上客人数、发车间隔等数据,计算每条线路每次公交停靠造成的乘客延误,如表3所示. 表3 公交停靠站乘客延误表 s 东西直行相位为本研究的优化相位,根据行人过街时间、周期长度、左转车辆到达率及优化相位现状绿灯时间,确定约束条件的约束量.第一相位最短绿灯时间为32 s,第二相位最短绿灯时间为18 s,第三相位最短绿灯时间为40 s,第四相位为13 s.社会车载客人数取1.6人/辆,公交车载客人数取29人/辆. 在约束条件的控制下,对控制目标函数进行试算,进行绿信比的调整,得到第三相位绿灯优化时间为8 s.优化后交叉口信号配时如图6所示,优化后的进口道通行能力折减量如图7所示,1 h总折减量为183 pcu/h. 图6 优化后交叉口信号配时图 图7 优化后进口道通行能力折减量统计图 由延误公式计算得到信号优化前后交叉口和公交站的乘客延误,其中站点乘客延误视为固定值不予以优化,各延误值如表4所示. 表4 优化前后交叉口-站点各延误对比表 s 从表中数据分析得到,通过对公交信号优先控制,使交叉口公交乘客延误降低了6%,社会车乘客延误降低了1.8%,乘客总延误降低了4%.说明本文提出的优化方法达到了公交信号优先控制的目的,一定程度上提高了乘客的出行效率. 利用VISSIM微观仿真软件的基本操作对本案例进行仿真验证,得到仿真效果图,如图8所示. 图8 仿真运行图 通过仿真数据的输出,得到信号控制优化前后的交叉口乘客总延误对比:优化前为354 500.365,优化后为 325 589.08.仿真结果表明,优化后交叉口乘客总延误下降了8%,相比于模型计算的结果有一定偏差.这是由于仿真只是为了验证优化前后延误变化的整体形势,故没有详细考虑路面状况以及交通流实际运行中可能出现的换道、超车等情况,而本文仿真结果确实验证了公交优先模型对交叉口交通运行效率具有优化效果. 通过本文的研究,在公交站点溢出情况下,考虑公交停靠对交叉口进口道通行能力的影响,在此基础上优化公交相位信号配时.研究结果表明,考虑了公交溢出影响的公交优先信号控制优化模型不仅有效降低公交车辆乘客延误,使公交车得到了优先通行权,提高了公交车服务水平,同时确保了社会车辆不受影响,达到交叉口乘客总延误相对最小的优化目标,对减缓交通流拥堵问题具有一定现实意义. 参考文献: [1]DIAB EHAB, EI-GENEIDY AHMED. Understanding the impacts of a combination of service improvement strategies on bus running time and passengers' perception[J]. Transportation Research Part A Policy & Practice, 2012, 46(3) : 614- 625. [2]BIAN BOMIN, ZHU NING , LING SHUAI. Bus service time estimation model for a curbside bus stop [J]. Transportation Research Part C: Emerging Technologies, 2015, 57 : 103-121. [3]左忠义, 汪磊. 公交到站时间实时预测信息发布技术研究[J]. 交通运输系统工程与信息, 2013, 13(1) : 63- 68. [4]GU WEI HUA, GAYAH VIKASH, CASSIDY MICHAEL. On the impacts of bus stops near signalized intersections: Models of car and bus delays[J]. Transportation Research Part B: Methodological, 2014, 68 : 123-140. [5]GU WEI HUA, GAYAH VIKASH, CASSIDY MICHAEL. Mitigating negative impacts of nearside bus stops on cars[J]. Transportation Research Part B: Methodological, 2013, 47(47) : 42-56. [6]LI RUI, ZHENG CHANG JIANG, LI WEN QUAN. Optimization model of tranit signal priority control for intersection and downstream bus stop[J]. Mathematical Problems in Engineering, 2016, 43: 1-8. [7]MA WAN JING, LIU YUE, HAN BAO XIN. A rule-based model for integrated operation of bus priority signal timings and traveling speed[J]. Journal of Advanced Transportation, 2013, 47(3) : 369-383. [8]YANG MIN, WANG WEI, WANG BO. Performance of the priority control strategies for bus rapid transit: Comparative study from scenario microsimulation using VISSIM[J]. Discrete Dynamics in Nature and Society, 2013, 11(1) : 1-9. [9]CHRISTOFA ELENI, AMPOUNTOLAS KONSTANTIONS, SKABARDONIS ALEXANDER. Arterial traf?c signal optimization: A person based approach[J]. Transportation Research PartC: Emerging Technologies, 2016, 66 : 27- 47. [10]QU DAYI, CAI GUO LIANG, CHEN XIU FENG, et al. Single point control strategy for realtime online transit priority[J]. Journal of Highway & Transportation Research & Development (English Edition), 2012, 6(2) : 71-76. [11]BHOURURI NEILA, MAYORANO FERNANDO, LOTITO PABLO, et al. Public transport priority for multimodal urban traffic control[J]. Cybernetics and Information Technologies, 2015, 15(5) : 17-36. [12]金勇, 姚荣涵. 单点交叉口固定信号配时优化模型[J]. 大连交通大学学报, 2011, 32(6) : 30-35. [13]HE HAI TAO, GULER ILGIN, MENDEZ MONICA. Adaptive control algorithm to provide bus priority with a presignal[J]. Transportatio Research Part C: Emerging Technologies, 2016, 64 : 28- 44. [14]VIKOVYCH IHOR, ZUBACHYK ROMAN. Bus lane within the area of intersection method for buses priority on the intersections[J]. Transport and Telecommunication Journal, 2015, 16(4) : 267-276. [15]YAO JIA, SHI FENG, AN SHI, et al. Evaluation of exclusive bus lanes in a bimodal degradable road network[J]. Transportation Research Part C: Emerging Technologies, 2015, 60 : 36-51. [16]LONG TRUONG, CURRIE GRAHAM, SARVI MAJID. Analytical and simulation approaches to understand combined effects of transit signal priority and road-space priority measures[J]. Transportation Research Part C: Emerging Technologies, 2016, 74 : 275-294. [17]许秀华. 公交车在公交停靠站的停靠时间研究[D]. 北京:北京交通大学,2015. [18]葛宏伟. 城市公交停靠站点交通影响分析及优化技术研究[D]. 南京:东南大学, 2006.1.3 站点溢出对乘客行程时间修正
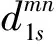

1.4 公交信号优先模型建立
2 实例验证
2.1 交叉口交通条件

2.2 信号配时优化

2.3 仿真结果分析

3 结论
