基于卷积神经网络和TensorFlow的手写数字识别研究

徐 胤， 袁浩巍， 李 智

上海电气集团股份有限公司 中央研究院 上海 200070

1 研究背景

手写字符识别可用于识别票据数字、车牌号等，应用广泛。字符识别可用传统的机器学习方法实现，如k-近邻算法、支持向量机、贝叶斯方法等。使用传统识别方法处理图像时，首先要对图像进行预处理，然后由人工设计特征提取方法。现有的特征提取方法有类哈尔特征、方向梯度直方图特征、尺度不变特征变换[1-2]、加速稳健特征等，这些特征提取方法各有优势，如类哈尔特征常用于人脸识别，方向梯度直方图特征常用于行人检测。特征提取后，将所得的特征导入一个分类器进行训练，得到分类器的相关参数。使用时，将待识别图像特征提取后，再输入经训练得到的分类器中进行识别。

人工神经网络的研究在一定程度上受到了生物学的启发，生物的学习系统是由相互连接的神经元所组成的复杂网络，人工神经网络与此大体相似[3]。神经网络具有广泛的应用范围，对于数据具有很好的鲁棒性，已成功应用于很多领域，如视觉识别、故障诊断、语音识别、机器人控制[4-5]等。卷积神经网络是人工神经网络的一种，其权值共享网络结构减少了权值的数量，降低了网络模型的复杂度，在图像识别应用中，可以将图像直接作为网络的输入。卷积网络是为了识别二维形状而设计的一个多层感知器，对平移、旋转、缩放具有高度不变性[6]，能够通过隐藏层逐层提取出图像特征。TensorFlow是由谷歌大脑团队开发的采用数据流图、用于数值计算的开源软件，通常用于机器学习和深度学习的研究，也可用于其它计算领域。TensorFlow具有灵活的架构，能够在多平台上展开计算，能够在中央处理器和图形处理器上运行，支持移动设备、服务器等，并支持Linux、Windows、Mac OS等操作系统，具有很强的可移植性。此外，TensorFlow支持多语言，可以使用C++、Python、R、JAVA等语言实现编程[7]。

笔者首先载入手写数字数据集，将数据集分为训练集和验证集；然后搭建具有两个隐藏层的卷积神经网络模型，输入训练集，设置模型参数和损失函数后进行训练，得到卷积神经网络的因数；最后使用训练出的卷积神经网络对验证集中的手写数字进行识别。

2 深度学习与卷积神经网络

传统神经网络通常采用反向传播算法进行特征训练。在随机给定一组权重因数后，得到网络的输出值，然后算出实际输出与目标输出之间的误差，将误差反馈至前面各层的节点，并更新每个节点的权值。逐步迭代这个过程，直至得到误差函数的全局最小值。

深度学习是在传统神经网络基础上发展起来的深度神经网络，其结构层次与神经网络相同，即包括输入层、隐藏层、输出层，且只在相邻层的节点之间有连接。为了克服传统神经网络训练过程中训练时间长、参数多等问题，深度学习使用了与传统神经网络不同的训练机制。卷积神经网络是一种在网络层中用卷积运算来代替矩阵乘法运算的神经网络，适合用来处理图像数据[8]。

2.1 网络结构

前馈型神经网络的连接方式采用多层结构，其基本结构为输入层、隐藏层、输出层。隐藏层也称中间层，隐藏层的层数大于等于1，包括卷积层、池化层、全连接层。图1为前馈型神经网络结构，从左至右依次为输入层、隐藏层1、隐藏层2、输出层。前馈型神经网络具有强大的非线性处理能力和模式识别能力。

图1 前馈型神经网络结构图

卷积神经网络是一种前馈型神经网络，图2为卷积神经网络结构[6]，有八层带权重因数的层数，第一层是数据输入层，之后连接的五层是卷积层，最后三层是全连接层，全连接层的最后一层为输出层。

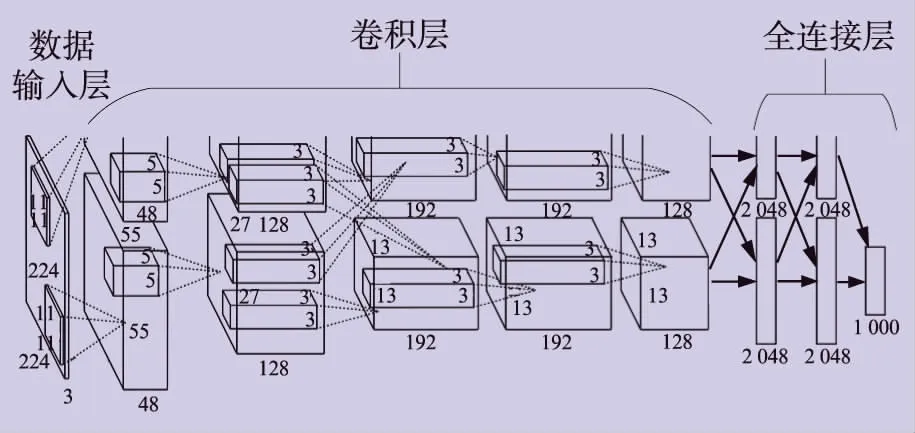
图2 卷积神经网络结构图

由图2可以看到，上下层神经元之间都形成了连接，假设隐藏层节点数量为10000，输入的图像分辨率为100像素×100像素，则仅一层隐藏层就有108个权值待训练，权值数量十分庞大。另一方面，图像具备固有的二维结构特征，如角点、直线、边缘等，这些局部特征都可以加以利用。卷积神经网络能够使一组神经元使用相同的权值，即权值共享，这样能够节省训练计算所占用的资源。

2.2 图像卷积

图像卷积能够自动提取图像中的特征，减少多余信息，用于神经网络中，具有代替人工设计特征的功能。图像卷积过程也称特征学习，特征学习能够自动适配新的任务，只需在新数据上进行训练，自动找出新的卷积核，可以避免繁重的特征工程。

卷积运算是针对两个实变函数的一种数学运算，用*号表示，其运算式为：

s(t)=(x*ω)(t)

(1)

式中：t为时间；x为输入信号；ω为核函数；s(t)为x在ω核函数下经过时间t后的卷积结果。

在处理图像卷积时，将二维图像I作为卷积运算的输入，分别在水平和竖直方向执行卷积操作，卷积规则为[9]：

S(i,j) =(I*K)(i,j)

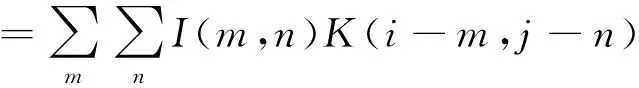
(2)

式中：K为二维卷积核；(i,j)为像素位置；(m,n)为卷积核尺寸；S(i,j)为卷积后得到的特征图。

在许多神经网络库中有互相关函数，这些函数和卷积运算比较相似，但没有翻转，也称为卷积运算，卷积后的图像为[9]：

S(i,j) =(I*K)(i,j)

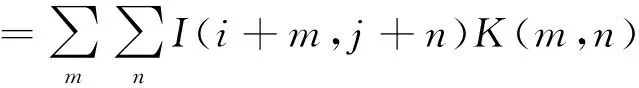
(3)

使用互相关函数的图像卷积过程如图3所示，卷积核在原图像上滑动，与原图像进行相乘和加权叠加后得到特征映射图。

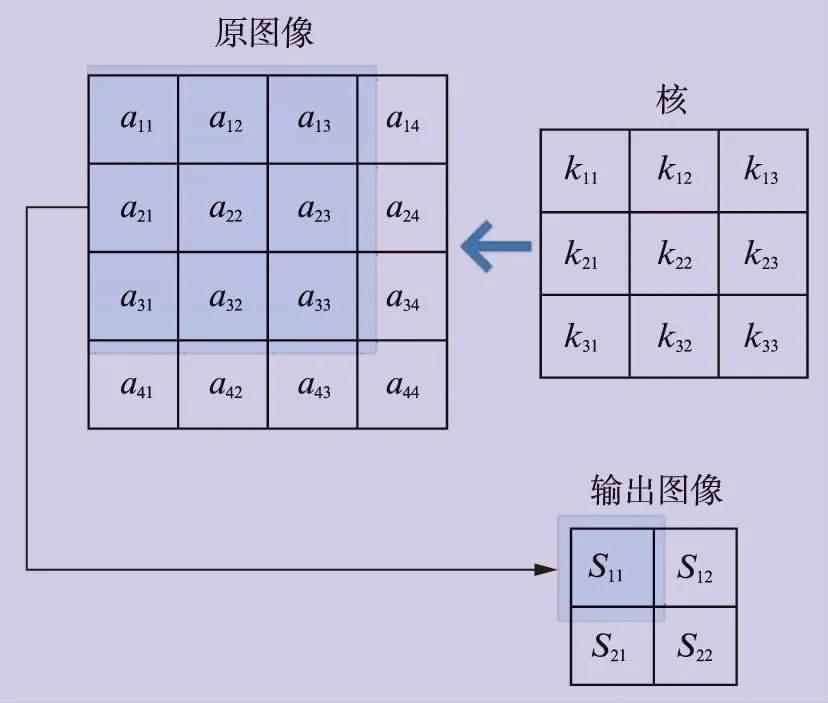
图3 互相关函数图像卷积过程

卷积核翻转的唯一目的是实现可交换性，但是这在神经网络应用中并不是一个重要的性质。而另一方面，互相关运算更简单，且更容易实现。

2.3 池化运算

池化指对卷积后的图像进行采样，以降低卷积图像的维数，即减少参数。另外，池化还能消除信号的偏移和扭曲，增强网络的鲁棒性。池化的方法一般有两种，一种是平均值池化，另一种是最大值池化。图4为最大值池化示意图，滤波器尺寸取为2×2，最大值池化运算时，在滤波器覆盖的每个区域中提取该区域内像素的最大值，进而得到主要特征。

图4 最大值池化示意图

2.4 激活函数

激活函数的作用是增加神经网络模型的非线性。如果没有非线性激活函数，那么神经网络的每一层输出就相当于上一层输入的线性组合。激活函数通常使用双曲正切函数或修正线性单元函数，作用于隐藏层，将前一层输入的数据非线性化。笔者使用的激活函数是修正线性单元函数，它不需要对输入进行归一化来防止饱和。使用修正线性单元函数时，卷积网络的训练速度远快于使用双曲正切函数[4]。修正线性单元函数的实现式为[10]：

fReLU=max(0,x)

(4)

修正线性单元函数的可视化图像如图5所示，横轴为变量x，纵轴为输出fReLU。

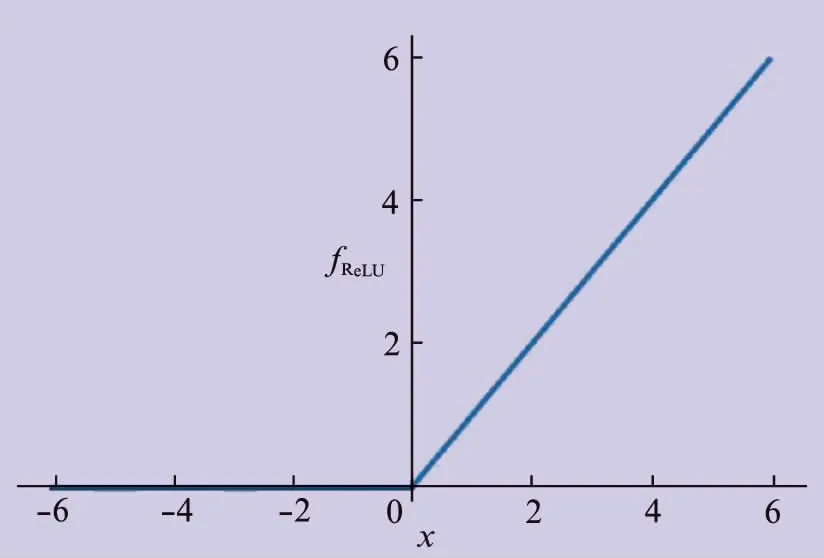
图5 修正线性单元函数可视化图像

3 训练流程

设置卷积网络的学习率LEARNING_RATE为1×10-4，设置训练的迭代次数TRAINING_ITERATIONS为3000，设置每次训练的样本数量BATCH_SIZE为50，设置验证集的大小为3000。

载入训练集数据后，将图像的像素值由0～255转换为0～1，代码为：

images = np.multiply(images, 1.0 / 255.0)

将权值因数、偏置因数初始化，通过随机数函数生成。随机数函数生成一组正态分布的随机数，这组随机数的值在[mean-2*stddev,mean+2*stddev]范围内。shape表示张量的维度，mean表示均值，stddev表示标准差，则有：

wei_init = tf.truncated_normal(shape, mean=0, stddev=0.1)

bias_init = tf.constant(0.1, shape)

笔者采用具有两层隐藏层的卷积网络。构造第一层卷积神经网络时，先进行卷积操作，再使用修正线性单元函数进行激活，然后进行最大值池化操作。使用相同的方法构造第二层卷积神经网络。构造卷积神经网络的代码为：

conv1 = tf.nn.relu(tf.nn.conv2d(image, wei_init, strides, padding))

pool1 =tf.nn.max_pool(conv1, ksize, strides, padding)

wei_conv2 = tf.truncated_normal(shape2, stddev=0.1)

bias_conv2 = tf.constant(0.1, shape2)

conv2 = tf.nn.relu(tf.nn.conv2d(pool1, wei_conv2) + bias_conv2)

pool2 =tf.nn.max_pool(conv2, ksize, strides, padding)

构造全连接层时，用随机数函数生成全连接层的权值后，使用修正线性单元函数进行激活，并使用dropout函数防止过拟合，构造代价函数，对代价函数进行优化，代码为：

pool2_flat = tf.reshape(pool2, [-1, 7*7*64])

fc1 = tf.nn.relu(tf.matmul(pool2_flat, wei_fc1) + bias_fc1)

fc1_drop = tf.nn.dropout(fc1, keep_prob)

y = tf.nn.softmax(tf.matmul(fc1_drop,wei_fc2) + b_fc2)

cost_y = -tf.reduce_sum(y_*tf.log(y))

train = tf.train.AdamOptimizer(1e-4).minimize(cost_y)

在理想情况下，应在每次训练中使用所有的训练数据，但是这样一来，计算量将十分大。考虑到计算代价，分小批次随机选择数据进行训练。这一方法称为随机训练法，计算量较小，而且不会对结果造成影响。

4 试验分析

4.1 试验数据

获得手写数字数据集，将数据集划分为训练集和测试集。数据集中的图像是手写数字的灰度图像，每张图片的分辨率为28像素×28像素，总像素为784，灰度值在0～255之间。训练集和测试集共有785列，第一列为该图的标签值，即该数字的真实值(0～9)，之后784列由对应图像展开得到。训练集包含42000幅图像，测试集包含28000幅图像。图6为训练集中随机抽出的图像。

图6 训练集图像

4.2 试验结果

从训练集的42000幅图像中抽出3000幅图作为验证集。将训练集中剩余的39000幅图像和验证集中的3000幅图像分别输入训练得到的卷积神经网络模型，得到若干次迭代训练后的训练集识别率和验证集识别率，如图7所示。

图7 训练集识别率和验证集识别率

图7中的试验结果显示，在经过2000次迭代训练后，验证集的识别率就已经达到了0.98。相信调整卷积神经网络参数后，识别率可以更高。

5 结束语

卷积神经网络已被广泛应用于学术界和工业界，用来完成图像识别任务。TensorFlow软件在网络构建、参数优化、模型训练等方面为用户提供了便利。

试验以手写数字集为例，显示了使用TensorFlow搭建卷积神经网络完成图像识别的效果，得到了有较高识别精度的网络模型，这对使用卷积神经网络和TensorFlow完成更复杂的图像识别任务具有参考意义。笔者下一步的工作是在具体应用场景下，深入理解深度神经网络的工作机制，研究如何更有效地选取网络参数。

[1] LOWE D G. Object Recognition from Local Scale-invariant Features[C]. Computer Vision, 1999. The Proceedings of the Seventh IEEE International Conference on, Kerkyra,1999.

[2] LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2)： 91-110.

[3] MITCHELL T M. 机器学习[M].曾华军，张银奎，译.北京： 机械工业出版社,2008.

[4] 徐胤,乐珺,袁浩巍.基于不变矩特征和RBF神经网络的图像识别[J].上海电气技术,2015,8(3): 33-36.

[5] 乐治后.基于RBF神经网络的光伏电池故障诊断[J].上海电气技术, 2015, 8(3): 28-32.

[6] KRIZHEVSKY A, SUTSKEVER I, HINTON G E, et al. ImageNet Classification with Deep Convolutional Neural Networks[J]. Communications of the ACM,2017,60(6): 84-90.

[7] ABADI M, AGARWAL A, BARHAM P, et al. Ten-sorFlow： Large-Scale Machine Learning on Het-erogeneous Distributed Systems[Z/OL]. http:∥arvix.org/abs/1603.04467.

[8] LECUN Y, BENGIO Y, HINTON G E, et al. Deep Learning[J]. Nature, 2015, 521(7553)： 436-444.

[9] GOODFELLOW I, BENGIO Y, COURVILLE A. Deep Learning[M]. Cambridge: MIT Press,2016.

[10] GLOROT X, BORDES A, BENGIO Y. Deep Sparse Rectifier Neural Networks[C]. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale,2011.