基于非下采样轮廓波变换的模糊图像质量评价
2018-04-18文继李丁立新万润泽
文继李,丁立新,万润泽
(武汉大学 计算机学院,湖北 武汉 430072)
0 引 言
根据是否有人的参与可以将模糊图像质量评价分为主观方法和客观方法两类。客观评价方法相比较于主观评价方法具有简单、实时、可重复、易集成等优势,成为图像质量评价体系中的热门研究方向[1]。客观图像质量评价算法根据依赖原始图像的程度可以将其分为全参考算法、部分参考算法和无参考算法[2]。目前无参考算法中针对某一种失真类型的研究成果较多,当中又以模糊失真类型为代表[3]。例如,Niranjan等提出了一种基于JNB的CPBD算法,具有不错的评价效果;桑庆兵等[4]提出了一种基于DCT的算法;Phong等[5]提出了一种基于快速小波的算法,用于全局和局部图像清晰度估计(fast image sharpness,FISH),以及此算法的变种基于块的FISH(block-based fish,FISHBB)算法;Leclaire等[6]提出了一种利用傅里叶相位信息清晰度指标进行盲去模糊的算法(s_index算法);Blanchet等[7]提出了一种基于全局相位相干的显式清晰度指数算法(S_Index算法)。本文提出了一种基于NSCT的无参考算法。该算法充分考虑了图像的频域性与多尺度性,在评价模糊图像时具有很好的鲁棒性和准确性。
1 非下采样轮廓波变换
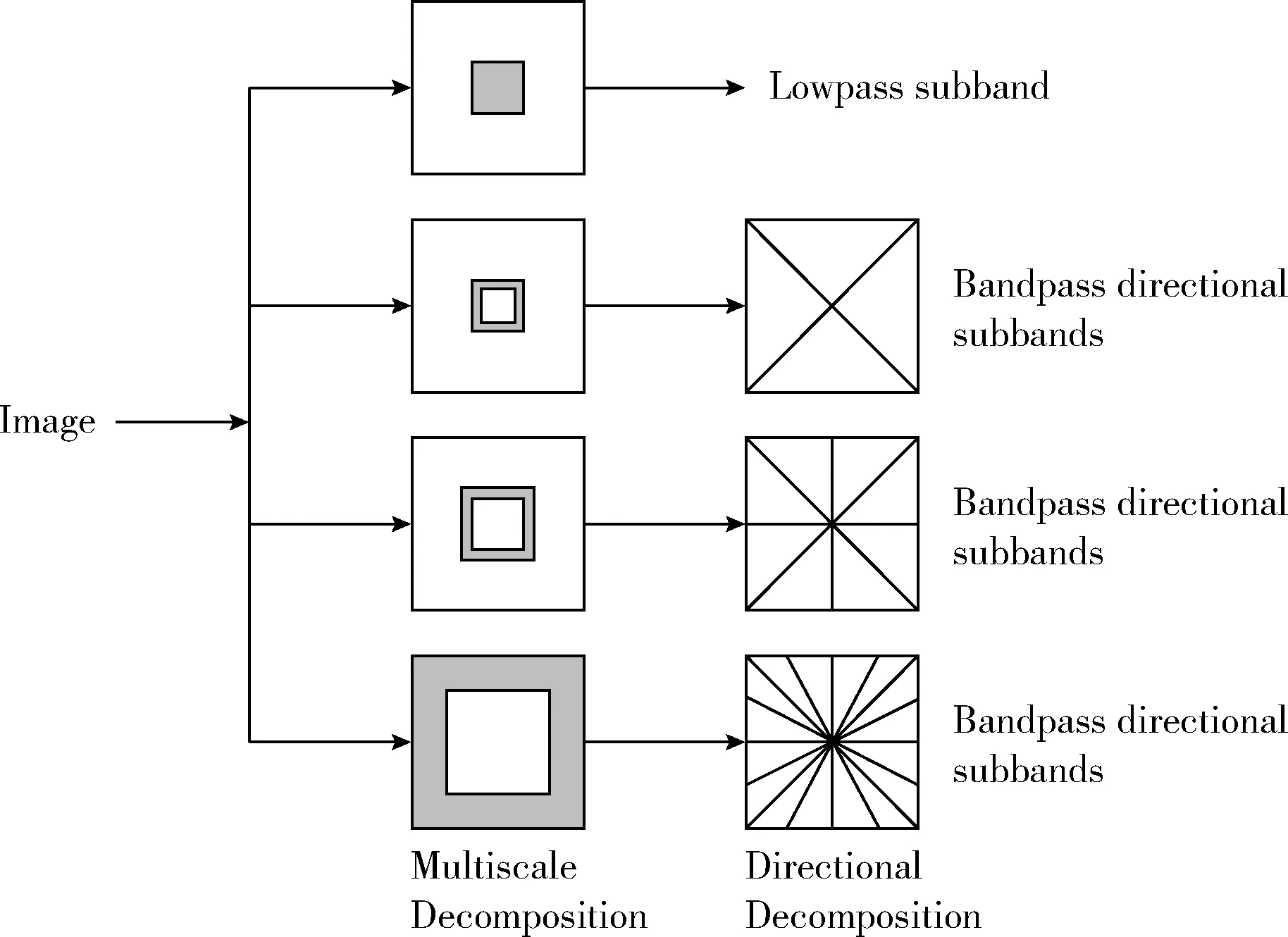
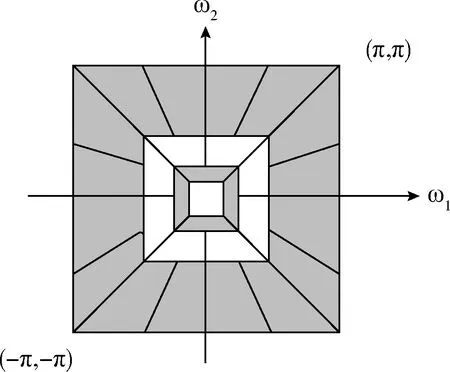
图像处理领域的研究人员经常把非下采样轮廓波变换应用到各种研究中[8-10],比如图像去噪、图像增强。非下采样轮廓波变换去掉了Contourlet两级变换中的下采样过程,构造了相应的非下采样滤波器,其结构如图1所示[11]。NSCT对应的滤波带具有更好的频域选择性和规则性,能够得到更好的子带分解。理想的频带分解如图2所示[12]。假设用I(x,y)表示图像,其中0 (1) 图1 非下采样轮廓波变换滤波器组结构 图2 非下采样轮廓波变换频域分解 由于非下采样轮廓变换的多尺度分解和方向分解这两个过程是相互独立的,出于这个原因可以将每个频带视为独立的并从中提取特征。 对于本文提出的方法NSCTBIQS,整体模型如图3所示。 图3 NSCTBIQS方法模型 正如前面所讨论的,将2D图像采用NSCT进行多尺度分解,得到原始图像4个尺度上的16个方向子带。滤波器选用“maxflat”和“dmaxflat7”。取每个子带的平均系数值作为特征,因此16个子带将产生16个特征,由此得到了一个维数为16的特征向量,这个特征向量包含了图像清晰度的相关信息。通过式(2)计算分解子带系数的平均值作为特征 (2) 式中:E为子带的特征值,N为每个子带的像素个数,C为子带的系数。 支持向量回归被广泛用于图像质量评价当中[13-15]。本文LIBSVM软件包进行支持向量回归,使用ε-SVR作为模型,径向基函数(radial basis function,RBF)作为内核函数。原始图像的第四级分解会得到16个方向子带,每个子带的平均系数作为特征,支持向量回归模型使用这些特征和数据集提供的DMOS评分进行训练。 在机器学习问题中,如果提取出的特征向量维数过大就会影响精度和性能。为了解决这个问题,需要使用一些特征选择算法用来降低特征向量的维数从而提升性能。序列后向选择(sequential backward selection,SBS)算法在特征数量不大时表现效果很好,因此本文选用SBS算法来选择最佳特征。 算法1: 序列后向选择算法 输入: 全部特征。 输出: 最优特征集。 (1)从特征全集开始, 令Fk={U}; (2)选择一个特征从Fk中剔除, 使得评价函数f*=argmaxJ(Fk-f)最优, 其中f∈Fk; (3)更新Fk-1=Fk-f*;k=k-1; (4)返回到(2)直到k=0。 令F={fj|j=1,…,16}是具有16个特征的特征集,目标是找到子集FN(N<16)使得目标函数J(FN)达到最优,J(FN)可以是以下3个函数中的任意一个。 J(FN)=SROCC(NSCTBIQ(FN),DMOSd) (3) J(FN)=PLCC(NSCTBIQ(FN),DMOSd) (4) J(FN)=RMSE(NSCTBIQ(FN),DMOSd) (5) 其中,NSCTBIQS(nonsubsampled contourlet transform blurred image quality score)表示非下采样轮廓变换模糊图像质量分数,DMOSd(differential mean opinion score of a database d)是数据集d的差分平均主观得分,SROCC(spearman rank order correlation coefficient)是斯皮尔曼等级相关系数,PLCC(pearson linear correlation coefficient)是皮尔逊线性相关系数,RMSE是均方根误差。对于式(6)和式(7),绝对值越大则相关性越强,对于式(8),值越小表示测量精度越高。斯皮尔曼等级相关系数定义如下 (6) 式中:di是数据库的第i个图像的主观DMOS等级和客观图像质量评分等级之间的差,i=1,2,…,N。皮尔逊线性相关系数定义如下 (7) (8) 式中:N是数据集D中的图像总数,xi是第i个图像的主观DMOS评分,yi是第i个图像的客观图像质量评分。 为了验证本文提出的方法有效性,我们在公开可用的图像质量评价的标准数据集上进行验证。本文使用了两种类型的统计分析方法来验证提出的方法是符合人类视觉系统(human visual system,HVS)特性的评价指标的。第一种类型的分析方法是评估预测单调性,式(6)中提到的斯皮尔曼等级相关系数(SROCC)是用于评估预测单调性的度量方法。另一种类型的分析方法是评估预测精度,式(7)中提到的皮尔逊线性相关系数(PLCC)和式(8)中提到的均方根误差(RMSE)是用于评估预测精度的度量方法。SROCC的值和PLCC的值越接近1就表示越接近于人类的主观感知。RMSE的值越低则误差越小,意味着更接近于人类的主观感知。 根据视频质量专家组(video quality experts group,VQEG)的推荐,客观算法对图像质量主观评价的预测值具有一定的非线性,因此,利用客观算法对图像质量评价时首先应当去除这种非线性因素,然后再进行相关性验证。本文选用的逻辑回归方法是 (9) 式中:β1,β2,β3,β4,β5是回归参数,Q和QP分别是回归前和回归后的预测图像的质量评分。随机选取实验数据集中80%图像作为训练图像,剩余的20%作为测试图像,保证训练和测试图像内容上完全独立。将训练图像经非下采样计算得到的特征向量作为输入,相应的DMOS值作为输出,利用ε-SVR模型训练得到图像质量预测模型。经随机选择训练和测试样本100次,得到平均测试结果。为了便于比较,用本文提出的方法与一些主流客观图像质量评价方法包括PSNR,SSIM,JNB,CPBD,FISH,FISHBB以及相位相干的方法(S_Index和s_index)进行对比实验并根据实验结果进行分析。 在LIVE数据集中,本文选用了从29幅参考图像生成的145幅模糊图像进行实验。表1给出了本文提出的方法NSCTBIQS与全参考图像质量评价方法,无参考图像质量评价方法的实验结果。可以看到,在LIVE数据集上本文提出的方法NSCTBIQS与无参考图像质量评价算法FISHBB效果相当,并且优于其它无参考图像质量评价算法和全参考图像质量评价方法。 表1 LIVE数据集实验结果 在VCL@FER数据集中,本文选用了从23幅参考图像生成的138幅模糊图像进行实验。表2给出了本文提出的方法NSCTBIQS与全参考图像质量评价方法,无参考图像质量评价方法的实验结果。可以看到,在VCL@FER数据集上本文提出的方法NSCTBIQS要优于表2中其它的方法。 在CSIQ数据集中,本文选用了从30幅参考图像生成的150幅模糊图像进行实验。表3给出了本文提出的方法NSCTBIQS与全参考图像质量评价方法,无参考图像质量评价方法的实验结果。可以看到,在CSIQ数据集上本文提出的方法NSCTBIQS与无参考图像质量评价方法FISHBB效果相当并且要优于其它无参考图像质量评价方法。 表2 VCL@FER数据集实验结果 表3 CSIQ数据集实验结果 在TID2013数据集中,本文选用了从25幅参考图像生成的150幅模糊图像进行实验。表4给出了本文提出的方法NSCTBIQS与全参考图像质量评价方法,无参考图像质量评价方法的实验结果。可以看到,在CSIQ数据集上无参考图像质量评价类算法中基于相位相干方法效果较好,本文提出的方法NSCTBIQS与基于相位相干的无参考图像质量评价方法s_index和S_Index效果相当并且要优于其它无参考图像质量评价方法。 表4 TID2013数据集实验结果 本文提出了一种利用非下采样轮廓波变换特点并结合机器学习中支持向量回归模型的模糊图像质量评价方法。正如实验结果得出的一样,本文给出的方法是符合人类视觉系统特性评价指标的。由于序列后向选择算法在特征数量较少时效果很好,但当特征数量较多时算法会非常耗时。诸如遗传算法,模拟退火算法等启发式算法可以提供更快速和有效的方式来选择期望的特征。如何结合更好的算法来进一步提高模糊图像质量评价效果将是未来工作的重点。 参考文献: [1]WANG Zhiming.Review ofno-reference image quality assessment[J].Acta Automatica Sinica,2015,41(6):1062-1079(in Chinese).[王志明.无参考图像质量评价综述[J].自动化学报,2015,41(6):1062-1079.] [2]Golestaneh SA,Karam LJ.Reduced-reference quality assessment based on the entropy of DWT coefficients of locally weighted gradient magnitudes[J].IEEE Transactions on Image Processing,2016,25(11):5293-5303. [3]ZENG Taiying,SHAO Xue,WANG Zuhui.No-reference blur image quality assessment based on local discrete wavelet transform[J].Journal of Optoelectronics·Laser,2016,27(7):754-760(in Chinese).[曾台英,邵雪,汪祖辉.基于局部离散小波变换的无参考模糊图像质量评价方法[J].光电子.激光,2016,27(7):754-760.] [4]SANG Qingbing,QI Huixin,WU Xiaojun,et al.No-refe-rence image blur assessment method based on DCT coefficients[J].Chinese Journal of Scientific Instrument,2013,34(11):2599-2604(in Chinese).[桑庆兵,齐会新,吴小俊,等.基于DCT系数无参考模糊图像质量评价方法[J].仪器仪表学报,2013,34(11):2599-2604.] [5]Vu PV,Chandler DM.A fast wavelet-based algorithm for global and local image sharpness estimation[J].IEEE Signal Processing Letters,2012,19(7):423-426. [6]Leclaire A,Moisan L.No-reference image quality assessment and blind deblurring with sharpness metrics exploiting Fourier phase information[J].Journal of Mathematical Imaging and Vision,2015,52(1):145-172. [7]Blanchet G,MoisanL.An explicit sharpness index related to global phase coherence[C]//IEEE International Conference on Acoustics,Speech and Signal Processing,2012:1065-1068. [8]WEI Xing,LIU Qing,GUO Yizheng,et al.Image denoising algorithm based on joint bilateral filter and multi-resolution analysis[J].Computer Engineering and Design,2016,37(12):3327-3333(in Chinese).[卫星,刘清,郭依正,等.联合双边滤波器耦合多分辨率的图像降噪算法[J].计算机工程与设计,2016,37(12):3327-3333.] [9]LIU Gang,ZHOU Heng,LIAO Xiaogeng,et al.Image re-gistration algorithm for infrared and visble light based on nonsubsampled contourlet transform[J].Computer Science,2016,43(11):313-316(in Chinese).[刘刚,周珩,梁晓庚,等.非下采样轮廓波域红外与可见光图像配准算法[J].计算机科学,2016,43(11):313-316.] [10]OUYANG Ning,ZHENG Xueying,YUAN Hua.Multi-focus image fusion based on NSCT and sparse representation[J].Computer Engineering and Design,2017,38(1):177-182(in Chinese).[欧阳宁,郑雪英,袁华.基于NSCT和稀疏表示的多聚焦图像融合[J].计算机工程与设计,2017,38(1):177-182.] [11]YANG Shu,WANG Yude.Image retrieval algorithm based on Contourlet transform and Hu invariant moments[J].Infrared and Laser Engineering,2014,43(1):306-310(in Chinese).[杨舒,王玉德.基于Contourlet变换和Hu不变矩的图像检索算法[J].红外与激光工程,2014,43(1):306-310.] [12]Lu F,Zhao Q,Yang G.A no-reference image quality assessment approach based on steerable pyramid decomposition using natural scene statistics[J].Neural Computing and Applications,2015,26(1):77-90. [13]Saad MA,Bovik AC,Charrier C.Blind image quality assessment:A natural scene statistics approach in the DCT domain[J].IEEE Transactions on Image Processing,2012,21(8):3339-3352. [14]SANG Qingbing,LIANG Dilin,WU Xiaojun,et al.No-reference quality assessment algorithm for blur and noise images using support vector regression[J].Journal of Optoelectronics·Laser,2014(3):595-601(in Chinese).[桑庆兵,梁狄林,吴小俊,等.基于支持向量回归的无参考模糊和噪声图像质量评价方法[J].光电子·激光,2014(3):595-601.] [15]SHEN Junmin,LI Junfeng,DAI Wenzhan.No-reference image quality assessment based on structure information and luminance statistics[J].Acta Electronica Sinica,2016,44(4):804-812(in Chinese).[沈军民,李俊峰,戴文战.结合结构信息和亮度统计的无参考图像质量评价[J].电子学报,2016,44(4):804-812.]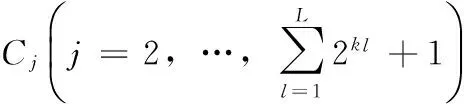
2 本文提出的方法
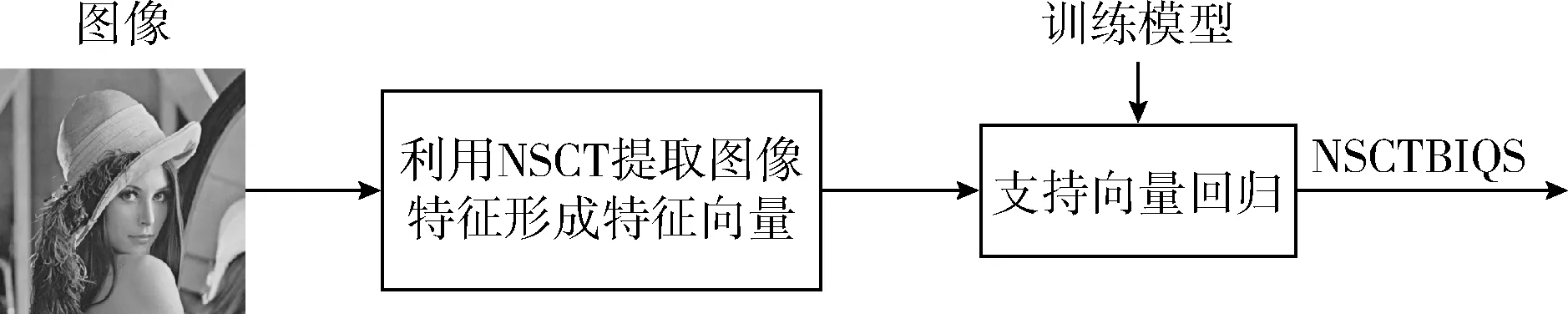
2.1 特征提取
2.2 支持向量回归
2.3 特征选择
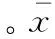
3 实验结果与分析
3.1 LIVE数据集

3.2 VCL@FER数据集
3.3 CSIQ数据集


3.4 TID2013数据集

4 结束语
