基于GPU加速的粒子流体动力学流血模拟算法

罗中粟　潘一源　唐良甫　朱珂权　李永强

1(浙江工业大学国际学院　浙江 杭州 310023) 2(浙江工业大学信息工程学院　浙江 杭州 310023)

0　引　言

近年来，微创手术[1]得到了快速的发展和广泛的应用。但是，因为微创手术本身的特点，医生需要透过内窥镜来观察患者体内的局部状况，这样就大大增加了医生的手术难度，而且对医生来说需要拥有一定的经验。因此，术前手术训练对医生来说就显得非常重要。虚拟手术训练系统利用触觉交互设备和计算机虚拟现实技术实现了手术过程的虚拟化，为医生提供了一个沉浸式的训练平台，被广泛应用于医学培训与手术计划中[2]。而组织形变与流血模拟等视觉效果是手术训练系统的重要组成部分。

真实的流血模拟大多采用光滑粒子流体动力学(SPH)方法[3]。将流体离散成带有属性和体积的粒子，结合有限元的思想为每个粒子求解方程得到下一时刻的状态，粒子的属性通过对周围邻居粒子的属性使用核函数加权求和得到。2003年Muller等[4]第一次将其用于流体模拟，然而，该工作未解决流体的不可压性。为了解决这个问题，Becker等在2007年将Tait方程引入SPH方法，实现了弱可压SPH，或简称WCSPH[6]。该方法部分解决了流体的不可压性，然而引入Tait方程的代价也是很大的，为了维持流体的稳定性，模拟的时间步长也必须相应缩短到10-5级，使得模拟的进程非常缓慢。Solenthaler等[11]在2009年提出了预估校正不可压SPH，即PCISPH，有效地解决了均匀密度单相流的不可压问题，模拟的步长也提升了两个数量级。但是，算法的计算量越来越大，其计算实时性问题一直是虚拟手术训练应用的瓶颈。

为了解决大量粒子条件下的实时性问题，首先我们使用PCISPH方法对粒子建模，然后对目标区域划分均匀网格并且使用最近相邻粒子搜索法遍历粒子，结果显示算法的效率明显提高。此外，本文使用CUDA技术[8-9]来提高计算的速度。同时本文采用一种改进的移动立方体方法对流体表面进行实时渲染，增强了手术训练真实性。

1　光滑粒子流体动力学

1.1　PCISPH算法

SPH是把流体离散成粒子的集合，每个粒子都携带着压强、速度、加速度等属性，对于空间中任意给定一点r的任意物理量A而言，使用SPH方法可以通过如下离散求和计算[10]：

(1)

式中：rj代表粒子j的位置，mj是指粒子j的质量，ρj表示密度，W(r,h)表示半径为h的光滑核函数。

SPH的一大优势在于物理量的空间导数可以直接通过平滑核的导数加权和得到，即：

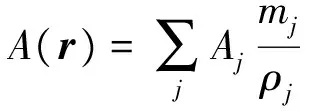
(2)

以及：

(3)

在欧拉公式中，等温流体由速度v、密度ρ和压力p描述。这些量随时间的变化由以下两个公式表示：

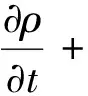
(4)

(5)

式中：g表示重力加速度，μ表示液体的粘度。在SPH方法中，粒子的质量和数量是恒定的，所以式(4)可以省略并且式(5)可以转换为：

f=-▽p+ρg+μ▽2v=fp+fg+fv

(6)

根据以上的规则，可以得到各个物理量的计算公式，如对于粒子i，它的密度可以通过领域的加权和计算：

(7)

压力：

(8)

粘性力：

(9)

由于平滑核的选择决定了SPH方法的稳定性、精确性和计算速度，我们使用了平坦和归一化的内核以便得到二阶精度的插值。我们设计了以下核函数：

(10)

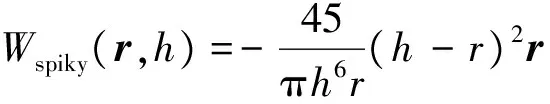
(11)

(12)

为了计算简便，本文使用一种不同但等价于文献[11]方式进行阐述。已知流体在不可压的情况下有：

(13)

(14)

若要使流体不可压，就需要使得粒子的密度变化率为0，于是就可以设上一时间点的粒子密度总是等于ρ0，这样便有：

(15)

PCISPH的算法流程如下：

(1) 对于全部的粒子建立空间索引。

(2) 根据粒子的加速度与时间步长得到下一时刻的速度和位置。

(3) 初始化压强和压力pi=0，Fp=0。

(4) 计算粒子在当前压力下的下一刻加速度、速度和位置。

(5) 计算粒子在这样的位置下的领域密度ρi，以及密度差Δρ=ρi-ρ0。

(6) 根据Δρ对压强pi进行修正，并计算新的压力Fp。

(7) 根据当前压力计算下一步速度和位置。

1.2　最近相邻粒子搜索法

为了提高 PCISPH算法的效率，我们使用最近相邻粒子搜索法遍历粒子，它的主要思想就是在目标域中构建临时的网格。我们构建的临时网格大小等于支持域的大小，在当我们计算某一个粒子的最近相邻粒子时，不需要遍历目标域中的所有粒子，而只需要遍历某个所在的网格和相邻的网格。此方法不仅缩小了研究问题的区域，而且减少了参与计算的粒子数目，这样，程序运算的效率就提高了。假设支持域为kh,那么我们构建临时网格的边长也为kh。在使用最近相邻粒子搜索法搜索的过程中，如果我们要搜索某一粒子i的最近相邻粒子，可以首先找出某一粒子i最近相邻粒子所在的区域范围，即他们要么处于和粒子i相同的网格内，要么处于和粒子i网格空间相邻的其他26个网格内，所以我们只需要搜索粒子i所在网格和相邻网格共27个网格内的粒子。程序流程如图1所示。

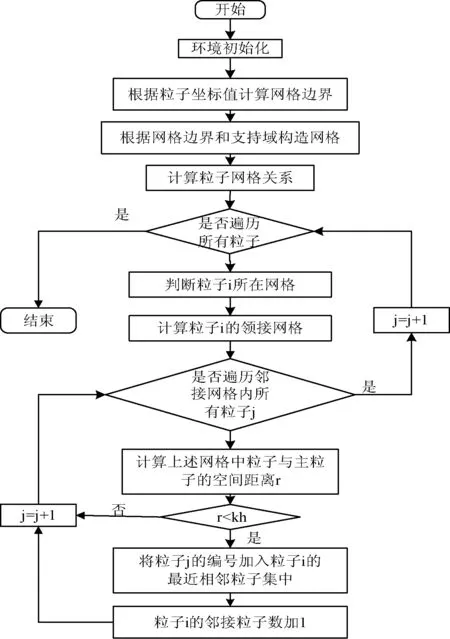
图1　最近相邻搜索法程序流程图

1.3　Cuda加速

在模拟流血的过程中，为了保证模拟效果的真实性同时使得流血模拟更加的灵活，粒子数目不得不增加，但是这样做会增加运算的负担，容易造成实时性的损害。为此，本文利用CPU和 GPU的并行运算，将所有可以并行执行的运算放在CUDA上计算来提高流血模拟以及虚拟手术训练系统的实时性。整个程序的系统如图2所示。

图2　GPU加速流程图

2　表面重建算法

为了得到真实的渲染结果，每进行一步的SPH模拟都要将点云转化为可着色的表面。本文的表面重建步骤如下:

(3) 对于三维密度场中每个体素，搜索其领域的粒子，根据体素中心到粒子距离进行插值得到密度，插值时将距离乘以Si进行调整。

(4) 对三维密度场进行立方体匹配，得到三角形网格。

(5) 对三角形网格进行表面细分，生成PN三角形，得到光滑的网格。

2.1　移动立方体算法

移动立方体[13]是一种经典的从密度场生成三角形等值面的技术。它把密度场均匀划分为格子，对格子的胞元的每个角点的密度场进行评估，根据其是否大于某个常量阈值来决定生成三角形的形式。它的步骤如下：

(1) 检查胞元立方体的12条边是否与等值面相交，如果边的两个端点中一个的密度小于阈值且另一个的密度大于阈值则判为相交，否则判为不相交。每条相交的边都生成一个对应的三角形顶点。

(2) 通过胞元的8个角点是否大于等值面生成一个8位的索引(大于等值面该位则为1，否则为0)。每个索引对应一种三角化的模式，因此通过索引便可得到哪些三角形顶点相连(如图3所示)。

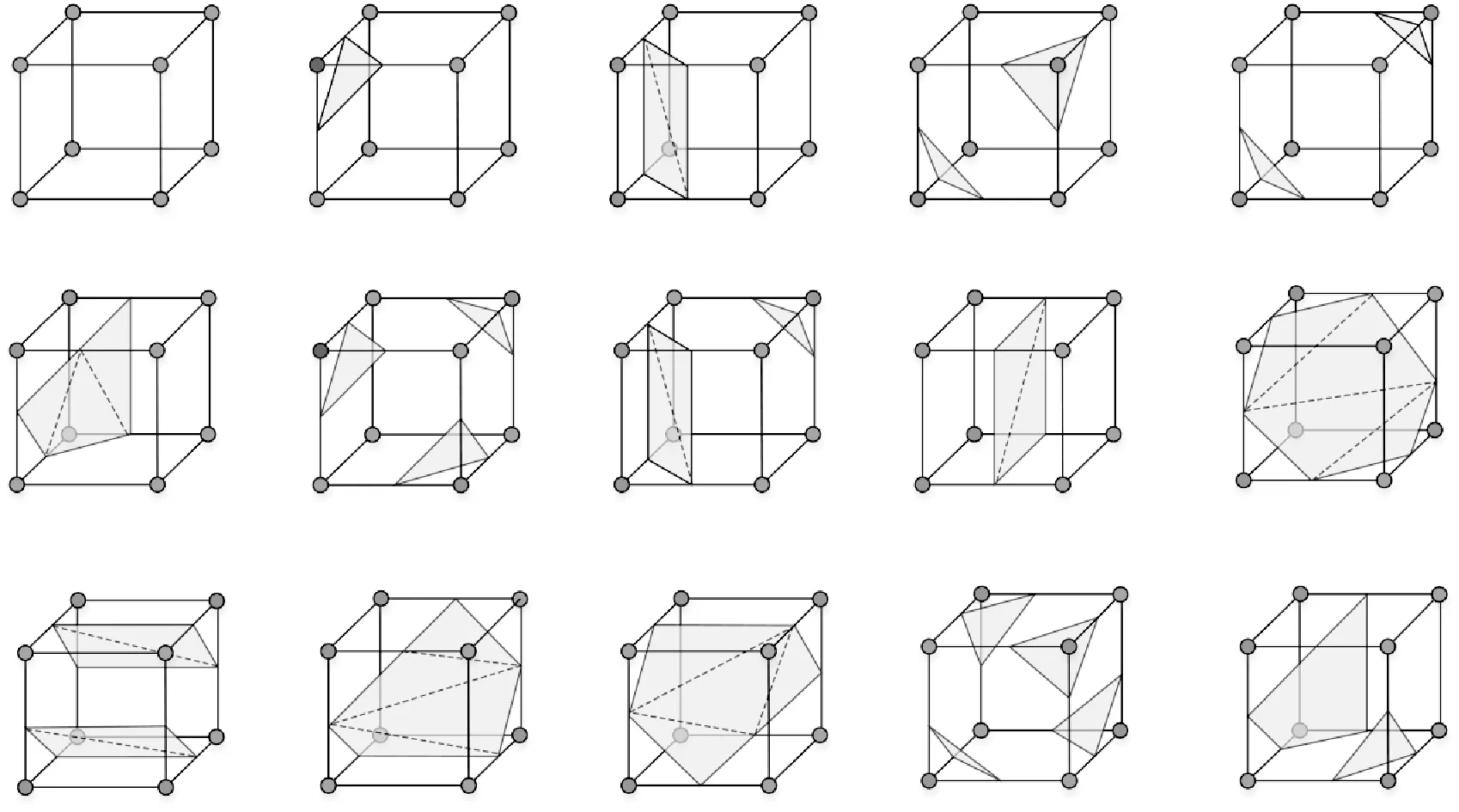
图3　Marching Cubes算法的15种基本情况

(3) 对密度场进行差分从而生成法线[14]：

(16)

当使用移动立方体算法时，我们需要计算离散点阵的每个单元格，因此生成的网格不够光滑。当我们以高分辨率绘制表面时，这种局限性将导致明显的多边形缺性。在本文中，我们使用PN三角形方法来平滑三角形网格边缘和为顶点着色操作提供更多的采样点。仅仅根据三角形的三个顶点及其法线就可以生成平滑的细分三角形。见图4。

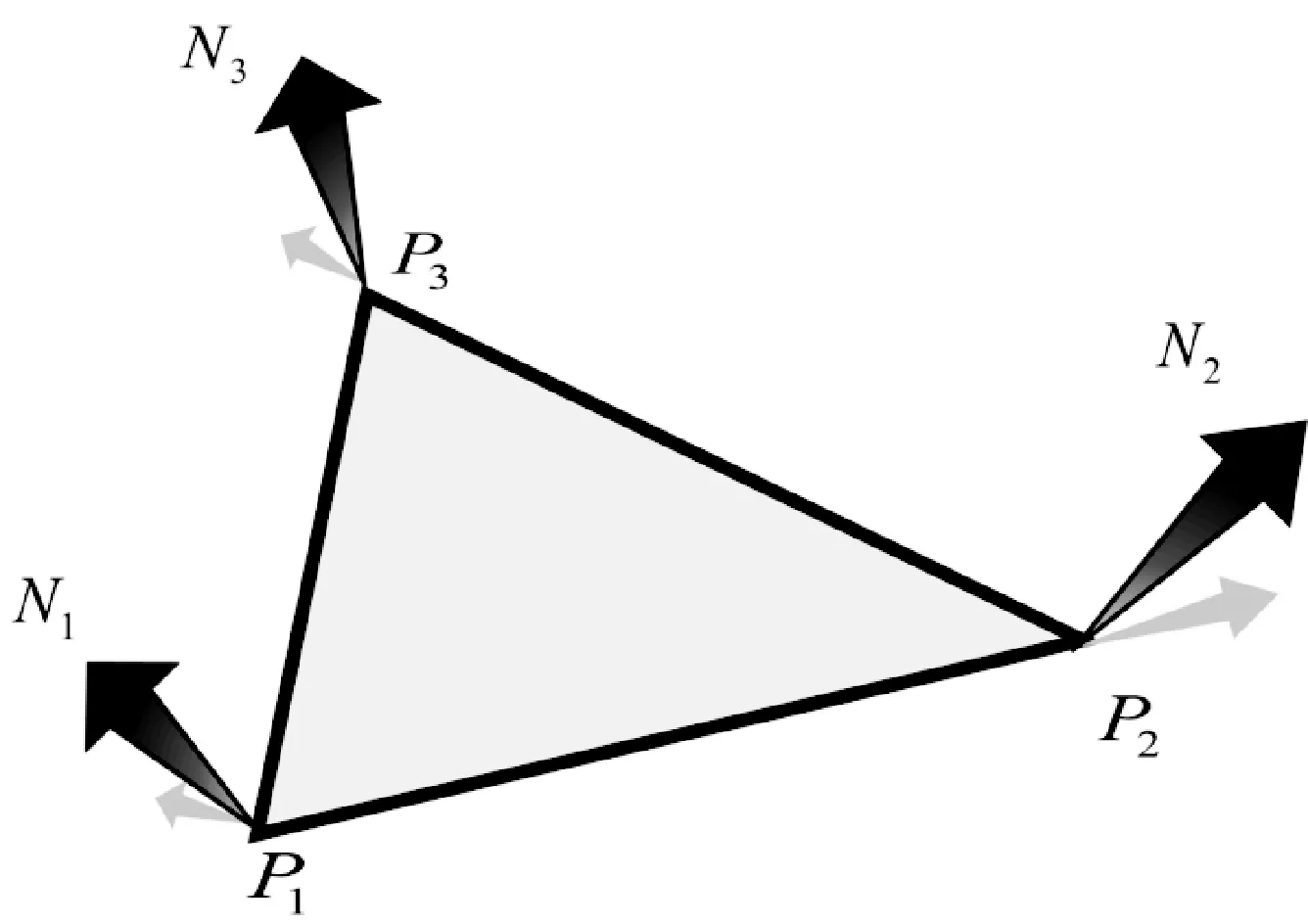
图4　输入数据：顶点Pi和法线Ni

如图4所示：给定顶点P1,P2,P3∈R3和各个点的法线N1,N2,N3∈R3。首先计算出其对应的Bezier曲面控制点bijk：

(1) 将bijk均匀分布在三角形上，三角形的三个顶点对应三个控制点b300、b030、b003。

(2) 在每个角，将其对应的两条边上的最近的点投影到与法线垂直的平面上，称为切点，如在b300可以生成两个切点b201、b210。以此类推在另两个角生成b102、b012以及b021、b120，如图5所示。

图5　三角的贝塞尔曲面排列而成的控制网的系数

(3) 将中心点朝六个切点的平均点移动，并越过移动的方向再移动1/2。

曲线PN三角形的系数和控制点用公式表示如下：

(17)

2.2　双边法线平滑

PN三角形可以解决网格过于粗糙的问题，然而，为了生成光滑的表面，仅仅用PN三角形是不够的。PN三角形细分出来的法线会导致照明呈凹凸状，这主要是由于立方体匹配生成的网格中有大量的窄条，而在被PN三角形细分之后，这些窄条形的三角形会生成更多窄条形的三角形，从而使网格质量显著下降，见图6。由于法线插值与三角形位置有关，因此低质量的网格最终会导致法线不平整。一般来说，为了提高网格质量，可以对模型进行重网格化，然而这类操作通常非常耗时，不适用于实时应用。

图6　使用PN三角形细分前后的网格

由于法线平滑与否主要影响屏幕绘制时的渲染效果，本文选择在屏幕空间对法线进行双边滤波的方法[15]来平滑法线。这样做的优势主要有：(1) 速度快，二维双边滤波可以使用两个分离的易于平行的一维滤波器近似；(2) 效果好，实验证明这种方法可以很好地去除光滑表面法线不平整的瑕疵。

首先将细分的网格光栅化至两张纹理中，分别以浮点向量存储位置以及法线信息。然后使用本文设计的双边滤波器对这两张纹理进行处理。本文定义它的形式为：

(18)

式中：Ω是像素的领域。

(19)

以及

(20)

该滤波器综合了空间位置以及法向量自身的信息对法向量进行平滑。它的设计概念主要源自两点：

(1) 由于观察到流体的表面曲率通常不高，几乎不会出现直角和锐角，因此像素的法向相似，更可能属于同一平面，应允许平滑，不相似的更可能属于不同平面，不应该平滑。

(2) 像素的空间位置相近的更可能在流体表面上测的距离相近，因此应允许平滑；空间位置相离较远的像素其测地距离通常更远，不应该平滑。

因此，本文定义衡量空间位置的函数为高斯函数的形式：

(21)

同时定义法线相似函数为：

g(nx,ny)=saturate(nx·ny)

(22)

式中：saturate(x)为将x截断到[0,1]的截断函数。

3　实验结果

本文所做的工作是在一个完整的病人特定的脑肿瘤切除模拟器开发的背景下提出的。该模拟器提供了两台力反馈机器，有限元组织模型和在切除期间进行拓扑适应的模拟，真实的视觉反馈包括高分辨率的纹理和照明，平滑的投射阴影、深度和流血。

表1显示了我们的方法在CPU和GPU条件下不同粒子数时的计算速度。实验结果表明虽然从CPU到GPU的数据传输需要很多时间，但使用CUDA技术显着提高了计算速度。随着粒子数量的增加，它能更有效地提高手术训练系统的实时性。

表1　采用CPU和GPU的模拟时间

此外，为了提高计算速度，我们使用最近相邻粒子搜索法来提高PCISPH算法的效率。图7显示了该方法相比全局搜索提高了PCISPH算法的效率。

图7　使用全员搜索方法和最近相邻粒子搜索法的PCISPH仿真时间

图8显示了SPH粒子的分布和进行表面渲染后的粒子分布。从图中可以看出，网格的边缘不是很平滑，所以在本文中，我们使用PN三角形法来细分三角形，结果表明，使用我们的表面重建算法后，表面变得更加光滑了。因此，我们的方法大大提高了虚拟手术训练系统的真实性。为了清楚地看到虚拟手术系统的实际操作，我们给出了在用于脑手术的虚拟手术模拟系统中直接渲染粒子的结果，如图9所示。

图8　不同方法对粒子表面渲染后的效果图

图9　虚拟手术模拟系统渲染粒子结果

4　结　语

本文提出一种方法，有效地将流血模拟集成到神经外科手术模拟过程当中。本文的方法实现了表面出血的真实模拟，包括抽吸和烧灼。本文采用PCISPH方法对血液进行建模并采用CUDA加速实现，展示了与切割仿真系统结合的表面流血效果。实验结果表明：本文模拟的流血效果具有良好的灵活性，能够满足不同的模拟需求，而基于GPU的实现大大提高了计算速度，满足了虚拟手术中实时性的要求。此外，本文所用的表面重建算法获得了逼真的出血效果，大大提高了手术训练系统的真实性。然而，如果我们想将此技术用于医院的实际外科手术训练中，该技术仍然有很多需要改进的地方。例如，在实际外科训练系统中，流血模拟必须与变形，吸取和切割相结合。此外，流血模拟的实时性和真实性需要进一步提高。我们将在未来的工作中进一步去研究。

[1] Puangmali P,Althoefer K,Seneviratne L D,et al.State-of-the-Art in Force and Tactile Sensing for Minimally Invasive Surgery[J].IEEE Sensors Journal,2008,8(4):371-381.

[2] Wang G,Zhang S,Xie H,et al.A homotopy-based sparse representation for fast and accurate shape prior modeling in liver surgical planning[J].Medical Image Analysis,2015,19(1):176.

[3] Monaghan J J.Simulating Free Surface Flows with SPH[J].Journal of Computational Physics,1994,110(2):399-406.

[4] Chen Z,Qin J,Si W,et al.Particle-based fluid simulation with small scale details[C]//IEEE International Conference on Information Science and Technology.IEEE,2014:561-564.

[5] Li Qiang,Yu Guichang,Liu Shulian,et al.Application of Computational Fluid Dynamics and Fluid Structure Interaction Techniques for Calculating the 3D Transient Flow of Journal Bearings Coupled with Rotor Systems[J].Chinese Journal of Mechanical Engineering,2012,25(5):926-932.

[6] Becker M,Teschner M.Weakly compressible SPH for free surface flows[C]//ACM Siggraph/eurographics Symposium on Computer Animation,SCA 2007,San Diego,California,Usa,August.DBLP,2007:209-217.

[7] Ihmsen M,Akinci N,Gissler M,et al.Boundary Handling and Adaptive Time-stepping for PCISPH[C]//The Workshop on Virtual Reality Interactions & Physical Simulations.DBLP,2010:79-88.

[8] Sanders J,Kandrot E.CUDA by Example:An Introduction to General-Purpose GPU Programming[M].Addison-Wesley Professional,2010.

[9] Zhou Y,Tan Y.GPU-based parallel particle swarm optimization[C]//Evolutionary Computation,2009.CEC’09.IEEE Congress on.IEEE,2009:1493-1500.

[10] Xiao C,Feng Y,Li Y,et al.Real-time and authentic blood simulation for surgical training[C]//Chinese Control and Decision Conference.2017:6832-6837.

[11] Solenthaler B,Pajarola R.Predictive-corrective incompressible SPH[J].Acm Transactions on Graphics,2009,28(3):341-352.

[12] Jin hanjun,Liu xiaoya,Liu xiaoyu.Collision Detection for Fountain Model Based on Partical System[C]//2010 3rd IEEE International Conference on Computer Science and Information Technology.IEEE,2010:502-505.

[13] Wang C,Chang T,Lin M.Reconstruction and Representation for 3D Implicit Surfaces[J].Communications in Computer & Information Science,2011,202(2):364-372.

[14] 王旭初,王赞.基于最近邻Marching Cubes的医学图像三维重建[J].计算机工程与应用,2012,48(18):154-158.

[15] 王鹏程.基于粒子方法的流体实时仿真研究[D].北京工业大学,2013.