基于k-means及改进k近邻的WiFi指纹定位算法

郭昕刚,　胡　朗

(长春工业大学 计算机科学与工程学院， 吉林 长春　130012)

0　引　言

近年来，随着移动互联网的快速发展以及无线WiFi的大量普及，基于位置的服务变得越来越流行。在室外环境中，全球定位系统(GPS)能够很好地实现定位。在室内环境中，由于建筑物的复杂结构以及室内障碍物的干扰，使得GPS技术在室内环境中受到了很大的限制[1]。而无线WiFi作为一种室内广泛分布的信号，其较强的稳定性以及传播距离远等特性，已经成为大量研究者青睐的对象。基于WiFi的定位技术中，常见的定位方法有：基于时间的定位(TOA)、基于角度定位(AOA)以及位置指纹定位[2]。位置指纹技术因不需要获取WiFi接入点的位置，是室内定位最为广泛的研究方法。位置指纹定位的主要问题是：离线数据库的建立以及在线实时的位置匹配。对于上述问题，文中研究了指纹库的建库原理，并将k-means聚类分析方法引入到WiFi定位技术中，提出了一种基于k-means聚类和加权的k近邻的位置指纹算法[3]。在离线建库阶段，采用k-means聚类方法将指纹库划分为不同的子类。在线定位阶段，将实测指纹与子类的类中心匹配，找到距离最近的类，在该类中找到相似指纹与之匹配[4]。针对位置估计算法，对现有的k近邻算法进行改进，引入了新的权重系数的计算方法。算法在定位环境下进行了仿真试验，验证了其有效性和实用性。

1　算法描述

1.1　离线指纹数据库的构建

离线采集过程包括两个阶段[5-7]:

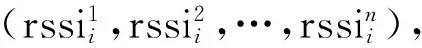
2)将采集到的指纹数据进行建库，假设在特定区域有m个采样点，可以检测到有n个WiFi信号强度RSSI信息。这m个采集点的位置事先经测量后已知，把采集到的各个AP的信号经处理后组成一个位置指纹数据库。这个指纹库可以表示：

(1)

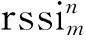
1.2　在线匹配定位

在线匹配阶段，即将待测目标实时测得的各个AP热点的信号强度与离线指纹数据库进行匹配，找到与待测目标指纹信息相似的一个或多个参考指纹点，再利用一定的匹配算法将指纹参考点的位置信息进行计算，最终求得待测位置的物理坐标。

目前常用的匹配算法有最近邻法(Nearest Neighbor)和k近邻法(kNearest Neighbor)。

1.2.1最近邻法

最近邻法就是通过在实时位置上测得的RSSI信息，经处理后，找出与该实时定位位置欧式距离最小的指纹点，实时位置与第i参考点之间的欧式距离为：

(2)

最近邻法是最基本的指纹定位算法，将最小欧式距离对应的指纹点的位置坐标作为目标位置的坐标。实际位置的坐标表示为：

(x,y)=mindi，i∈[1,m]

(3)

最近邻法的定位原理简单，耗费时间短，但该方法存在很大的定位误差，由于信号采集的不稳定性，单纯的从最短欧式距离的一个采样点坐标作为定位目标势必会造成结果的不准确。

1.2.2k近邻法

k近邻法是对最近邻法的改进，即首先将实时指纹同数据库中所有参考点遍历计算欧氏距离，再对欧式距离从小到大进行排序，然后选出前k(k≥2)个欧式距离较小的点，并将k个指纹点对应的位置坐标求均值作为目标位置。实际位置的坐标表示为：

(4)

式中：(xi,yi)----指纹数据库中第i个指纹点对应的位置坐标；

(x,y)----实际定位结果坐标。

k近邻法相对于最近邻法有一定的改进，但k近邻法未考虑到不同参考点对待测目标的贡献程度，即距离近的参考点对待测目标的位置估算贡献程度大，距离相对较远的参考点对待测目标的位置估算贡献程度小。不同参考点对待测目标的影响程度并不相同，所以对每个参考点赋予相同的权重对估算后的位置精度势必有一定的影响。

2　k-means聚类+改进的k近邻算法

文中在对位置指纹算法的深入分析和研究下，提出了一种基于k-means聚类和改进的k近邻融合算法。在指纹库建库阶段，利用k-means聚类把指纹信息相似的参考点分成一类。在位置估算阶段，实测指纹与聚类后的指纹类进行匹配，找到与实测指纹最相似的一类，然后运用改进的k近邻算法计算待测目标位置。其具体的工作原理如图1所示。

图1定位工作原理图

2.1　k-means聚类算法对指纹库进行优化

位置指纹库初步建成之后，文中将对指纹库进行聚类处理[8]。k-means聚类方法的具体执行过程如下：

1) 输入m个指纹和聚类个数k(k≤m)；从m个指纹中任意选取k个指纹作为初始聚类中心。

2) 对于剩下的(m-k)个指纹，计算每个指纹到各个聚类中心的距离dij，dij表示第i个指纹点到第j个聚类中心的距离，找出指纹点到各个聚类中心的最小距离dmin，并将该指纹点划分到与其距离最小的聚类中心所在的类。

3) 重复步骤2)，直到将所有剩余的指纹点划分到属于自己的类中，组成k个聚类(G1,G2，…,Gk)，每个类都包含其聚类中心及其对应的指纹点。

4) 计算各个类中的聚类质心，如果求得的质心和聚类中心相同，表示聚类结束。否则令聚类质心为其新的聚类中心，重新对各个指纹点进行聚类，直到最后的质心等于上一次的聚类中心为止。

5) 输出聚类结果。

k-means聚类的算法流程如图2所示。

图2　k-means聚类流程图

2.2　改进的KNN算法

为了有效解决KNN算法存在的参考指纹单一、定位结果不准确的问题，文中提出了一种改进的KNN算法。其具体操作过程如下：引入权重系数ωi，其表示不同参考点对待测定位点的贡献程度，一般来说，距离远的参考点对待测定位点的贡献程度小，距离近的参考点对待测定位点的贡献程度大[9]。权重系数的推导公式如下：

(6)

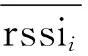
σi----第i个参考点指纹的标准差。

令

(7)

则权重系数为：

(8)

目标位置的估计坐标为：

(9)

3　定位误差的评价指标

算法的定位效果一般采用两种指标来表示[10]：一种是定位误差累计概率；一种是均方根误差。定位误差累计概率一般表示为

P(e)=p(e≤e0)

0≤P(e)≤1

其分布曲线的收敛速度表示定位误差的大小，收敛速度越迅速，表示误差越小，反之定位误差越大。

均方根误差的计算公式为：

(10)

式中：(xest,yest)----待测位置的估计坐标。

均方根误差越小，表示待测位置的计算越准确，反之表示计算的待测位置越不精确。

4　实验仿真与分析

为了验证k-means聚类和改进的k近邻融合算法的性能，文中运用MATLAB软件对算法进行了仿真，并对原有的KNN算法和NN算法进行了比较，验证了改进后算法的优势[11-14]。

4.1　实验环境的搭建

实验选择的定位区域为长春工业大学南湖校区老图书馆3楼西侧走廊，在走廊区域能够检测到设置的AP热点。选择走廊中2.5 m×60 m的方形区域，走廊地面铺设有正方形瓷砖(规格为0.8 m×0.8 m)，以3302和3303门口为起点，每隔两块瓷砖(1.6 m)作为一个采样点，共设置100个采集点，左右各50个。信号强度监测装置采用智能手机APP，手机型号为MG4J2CH/A,处理器为双核1.4 GHz,系统为iOS 11.2.1，APP为WiFi信号强度检测器。在每个采样点上每隔1 s采集1次数据，采集30次。定位区域平面图如图3所示。

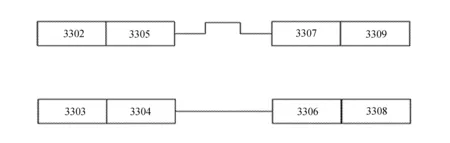
图3定位区域平面图

4.2　k-means聚类算法对指纹库的优化

为了验证经k-means聚类算法优化后的指纹库的定位效果比未经优化的指纹库定位效果好，文中首先在同一区域采集相同的指纹点，采用相同的匹配算法，在同一定位点处分别采取两种方法进行多次实验，并对记录结果进行对比分析。

经单次k-means聚类后的效果对比图如图4所示。

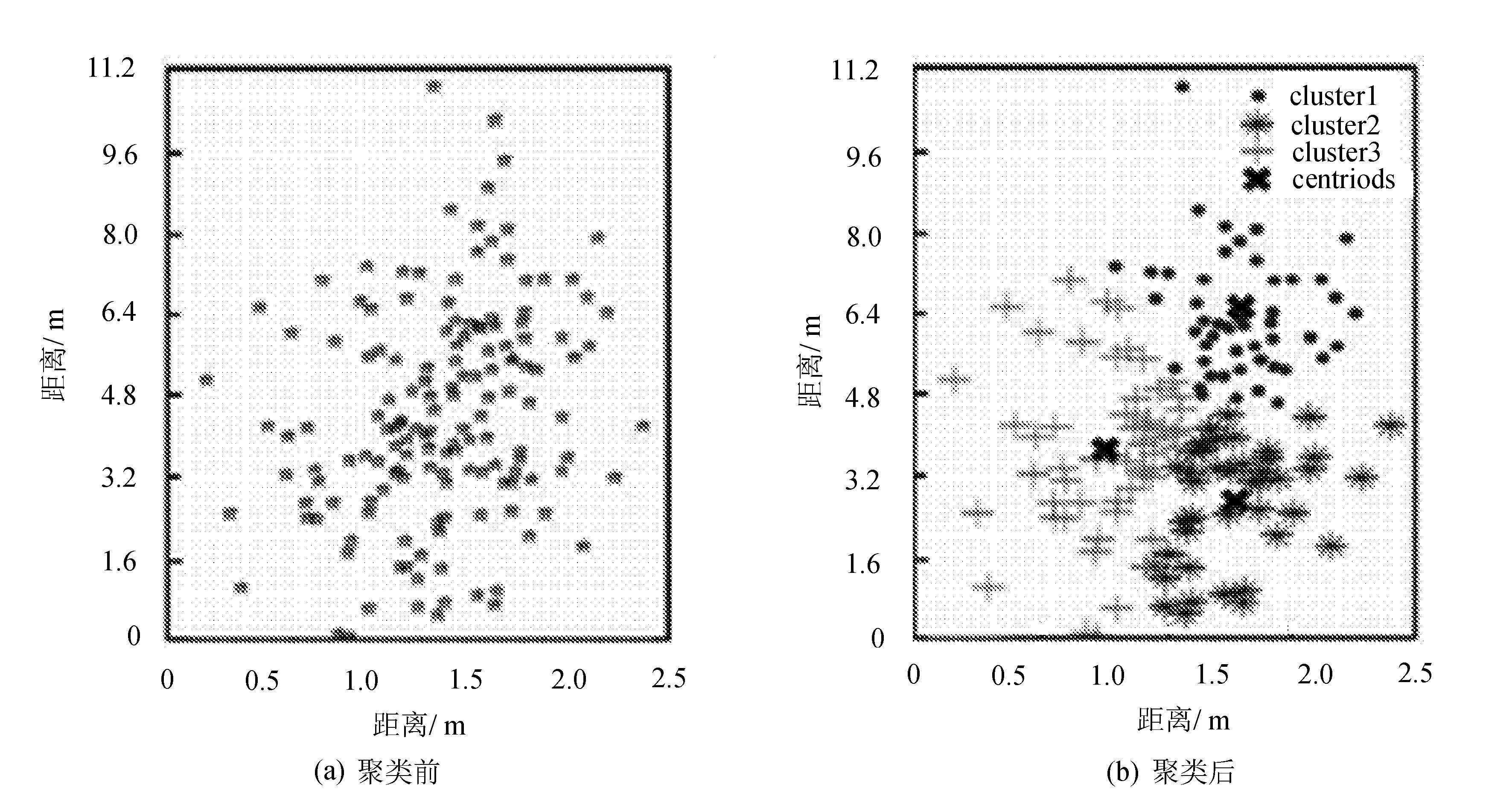
图4实验样本空间数据聚类前后对比图

指纹库优化前后使用同一种算法实验的误差对比图如图5所示。

图5　指纹库优化前后误差概率对比图

经对比分析发现，通过k-means聚类后的指纹库能有效地把具有相似特征的指纹点聚成一类，图4中将离散的数据点分成了三类，并定义了每个类别的中心，有效地降低了在线匹配的搜索空间。图5表明，使用同一种匹配算法，指纹库聚类和指纹库没有聚类的差别，经指纹聚类后的算法误差平均误差概率提高了20%，比没有聚类前的算法效果更好。

4.3　改进的k近邻算法(WKNN)对k近邻(KNN))和近邻算法(NN)的提高效果

由于k-means聚类算法与改进的k近邻算法(WKNN)以及k近邻算法都涉及到k值的选取问题，所以,首先对k-means聚类算法和k近邻算法中k值大小对定位误差的影响作出探究，找到能使定位误差达到最小的k值。下面是一组采用原始数据而k取值不同时的误差分析,见表1。

表1　k-means-KNN平均定位误差表

由表1可见，在k-means聚类算法k取3，KNN算法k取4时，达到的平均定位误差最小。在接下来验证试验中，我们将取同样的k值去进行实验。为了验证文中改进后算法的定位效果，在图4表示的定位场景中，分别使用3种不同的定位算法(WKNN、KNN、NN)进行实验:

1)算法是文中提出改进的k近邻算法(简称WKNN算法);

2)原始的KNN算法，其被选取的k个参考点均被赋予相同的权值1/k；

3)近邻算法(NN)，选取欧式距离最小的点的位置作为待测目标的位置。

实验使用的数据指纹库都是经k-means聚类后的同一指纹库。

利用上述3种方法对50个定位点处采集的数据进行仿真实验，分析计算得到的定位误差累计概率图如图6所示。

图6　WKNN/KNN/NN三种算法定位精度对比图

从图6可以看出，文中提出WKNN算法收敛距离在1.25 m左右，而KNN算法的收敛距离在1.5 m左右，NN算法收敛距离在1.8 m左右。WKNN算法引入了权重系数之后，定位结果的误差有所降低，定位精度获得了一定的提高，说明了提出WKNN算法具有一定的可行性。

5　结　语

针对传统的指纹定位算法定位精度不高以及指纹库匹配搜索范围大的问题，进行了深入的分析，提出了一种基于k-means聚类分析方法以及WKNN的在线匹配算法，并在现实场景中进行了实验验证，结果表明，提出的定位算法在精度以及稳定性方面具有一定的提升，对基于位置指纹的室内定位研究提供了一定的参考作用。

参考文献：

[1]Xia Mingzhe, Chen Jiabin, Song Chunlei, et al. The indoor positioning algorithm research based on improved location fingerprinting[A]. Chinese Control and Decision Conference(CCDC)[C].2015.

[2]王淑婷.基于位置指纹的WiFi定位算法研究[D].长春：吉林大学，2015.

[3]杨帆.基于改进KNN算法的室内WiFi定位技术研究[D].西安：西北工业大学，2016.

[4]毛永毅，杨强强，徐萍.基于WiFi的一种改进的室内定位算法[J].测控技术，2017,36(8)：26-30.

[5]Leu J S, Yu M C, Tzeng H J. Improving indoor positioning precision by using received signal strength fingerprint and footprint based on weighted ambient Wi-Fi signals[J]. Computer Networks,2015,91:329-340.

[6]吴泽泰，蔡仁钦，徐书燕，等.基于K近邻法的WiFi定位研究与改进[J].计算机工程，2017,43(3)：289-293.

[7]Wang F, Huang Z, Yu H, et al. EESM-Based fingerprint algorithm for Wi-Fi indoor positioning system[C]//Ieee/cic International Conference on Communications in China,2013:674-679.

[8]王磊，周慧，蒋国平，等.基于WiFi的自适应匹配预处理WKNN算法[J].信号处理，2015,31(9)：1068-1072.

[9]王青.WiFi室内定位系统的设计与实现[D].北京：北京交通大学,2014.

[10]陈斌涛，刘任任，陈益强，等.动态环境中的WiFi指纹自适应室内定位方法[J].传感技术学报,2015(5):729-738.

[11]郭昕刚，李航，宫鸿,等.基于边界过滤和邻域均值滤波的室内定位算法[J].长春工业大学学报，2017,38(5):426-432.

[12]孙苑莹.无线网络的移动节点定位方法研究[J].长春工业大学学报，2015,36(1)：57-60.

[13]唐洋，白勇，马跃，等.基于WiFi的指纹匹配法在室内定位中的应用研究[J].计算机科学,2016，43(5)：73-75.

[14]刘志鹏，袁敏.一种基于WiFi的改进型室内位置指纹定位方法[J].计算机与现代化,2016(4):36-39.