露天矿复合边坡动水携砂蠕变模型研究

2018-04-17，，，，

长江科学院院报 2018年4期

，，，，

(辽宁工程技术大学 a.土木工程学院; b.力学与工程学院，辽宁阜新　123000)

1　研究背景

在我国内蒙古地区薄基岩上覆含水厚松散层地质条件下的露天开采过程中，由于受降水过程中渗流作用的影响，地下水系及地表水系发生剧烈的调整。细砂粒随着水在地层内的渗流过程被携带出来，形成大面积的水砂混合物堆积于地表，也形成坡内潜蚀和破坏，使得边坡稳定性降低，严重危及边坡和生产安全，且破坏一旦发生，难于治理，严重破坏周边自然生态环境。

这类现象属于矿山开采诱发水害中第四系松散含水层型水害的一种[1]，从机理上属于高水头差所形成的渗透压力作用下，水砂运移所引发的岩土体渗透破坏现象，且其机理明显有别于其他渗透破坏特征，发生条件更加复杂。

关于砂土动水携砂现象的专门研究相对较少，与其相关的研究主要集中在地震及渗透液化、管涌与矿山灾害中的溃砂现象几个方面。

汪闻韶[2]对液化进行了分类并从机理上解释了砂土液化现象。Bardet等[3]研究了San Francisco Loma Prieta地区地震砂沸现象的分布与地面位移的关系。Holzer等[4]研究了非地震荷载引发的砂沸现象。Casagrande[5]最早分析了砂土液化引起的往复循环变形。邓荣贵等[6]从砂粒-孔隙水两相介质相互作用角度，根据下沉砂粒与渗流孔隙水间相对运动过程的动力作用建立饱和砂土液化过程模型和判据。刘红军等[7-8]构建了海床土体微单元破坏的重正化群模型，对结构面断裂损伤临界概率进行了研究。周健等[9]求解了两相介质流体连续方程与Navier-Stoke方程，模拟了不同水压渗流引起的液化过程。李广信等[10]通过模型试验模拟二元堤基条件与不同深度防渗墙管涌发生、发展过程，获得出砂面积，验证渗透破坏模式。刘忠玉等[11]构建了毛管模型，推出颗粒起动临界水头梯度公式和考虑细颗粒流失的渗透系数公式。李守德等[12]针对管涌破坏渗流场强烈的空间特性提出以一维通道嵌入三维块体的方法，分析了渗流场时空分布特性。刘丹珠等[13]对考虑土体坍塌的单层堤基管涌过程的数值模拟方法进行了研究。隋旺华等[14-15]用带裂缝混凝土块模拟带裂缝岩体采动过程，采用改装渗透仪对采煤垮落带和裂缝带渗透破坏机制进行了研究。杨伟峰[16]设计制作了水砂混合流运移及突涌试验模型，模拟覆岩体裂隙通道中水砂混合流在运移与突出过程中的起动、运移、稳定过程。

露天矿复合边坡发生的动水携砂现象与其他渗透破坏的特点明显不同。目前，对于动水携砂现象的致灾机理研究相对薄弱。为揭示露天矿复合边坡内砂粒间相互作用机理，需要对砂粒特征结构单元进行受力分析，建立简化蠕变力学模型。现有的滑片元件仅能反映摩擦滑动阶段的变形，无法反映塑性区域扩展至形成塑性铰后的转动过程，给描述砂土颗粒间强力链上的变形和力学行为带来了困难，而塑性铰恰好可以解决这个问题。

本文尝试通过引入塑性铰概念，尝试用“塑转铰”元件代替滑片元件，描述塑性变形阶段中塑性区的形成、扩展、形成塑性铰后的转动过程，构建可用于分析砂土颗粒间变形、移动演化过程的砂土蠕变接触力学模型。

2　一种新的“塑转铰”元件

2.1　基本物理模型元件

岩土体物理模型通常由基本元件(完全弹性弹簧、黏壶和滑片)分别模拟理想弹性固体(Hooke solid model)、牛顿流体(Newtonian liquid model)和圣维南理想塑性固体(St.Venant plastic solid model)，并将2种或2种以上基本元件串联或并联起来，进行各种排列组合，就能近似而定性地模拟真实岩土材料的力学性能，并以应力和变形的关系推导出岩土体流变方程。

2.2　“塑转铰”元件的提出

塑性铰的概念出自钢筋混凝土结构设计。适筋梁或柱受拉弯、压弯作用纵筋屈服后，截面可以有较大转角，形成类似于铰一样的效果，称作塑性铰。塑性铰是一种特殊的铰，能承受一定方向的弯矩，这是它区别于一般铰最本质的特征。塑性铰不是集中在一点，而是形成一小段局部变形很大的区域；塑性铰为单向铰，仅能沿弯矩作用方向产生一定限度的转动，而理想铰不能承受弯矩，但可以自由转动。由于颗粒单元在受力变形过程中会受剪切力作用，颗粒间发生摩擦、滑动和转动的过程，尝试引入塑性铰概念，构建一种新型元件来描述砂土颗粒接触区域内发生塑性挤压变形后形成一定的塑性区域并发生有限转动的过程。

基于现有滑片元件不能描述发生塑性变形后，在局部一定区域形成塑性铰后发生转动的过程，提出一种新的简化模型元件来代替滑片元件，对滑片元件进行改进，见图 1。图1中，σ为法向应力；M为弯矩。当元件未达到最大剪切强度时仍为滑片元件，但当元件达到并超过最大剪切强度发生滑动后，由于塑性区的扩展，形成塑性铰时，元件由滑片转变为塑性铰，称其为“塑转铰”元件。

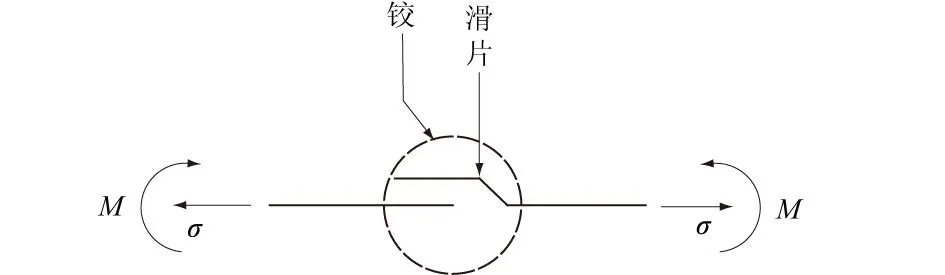
图1　塑转铰元件Fig.1　Plastic-to-hinge element

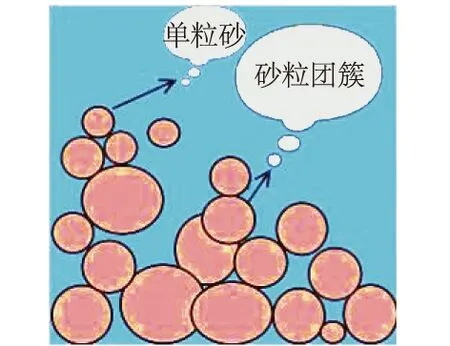
图3　砂土颗粒细观结构示意图Fig.3　Schematic diagramof mesoscopic structure ofsand particles

3　砂粒团簇特征结构单元力学模型

3.1　砂土颗粒细观特征结构单元力学分析

颗粒物质与湍流被世界公认并列为100个科学难题之一。如何建立微细观与宏观间的联系也是颗粒物质宏细观研究的一个瓶颈。目前对颗粒物质体系平衡和运动规律及其应用的研究形成一门新的学科——颗粒物质力学。通过采用高精度电子天平称重法、显色灵敏复写纸压痕法和光弾性法等方法和实验手段已检测到颗粒物质中截面上的接触力分布情况，确认了力链的存在(见图2)[17-18]，并对强力链上颗粒间接触力进行量化分析，但仍无法检测弱接触力，无法排除对内部接触力的干扰。对于颗粒间的接触力、颗粒物理性质、初始和边界条件等对接触力及强力链分布的影响仍需进一步研究。

图2　重力作用下砂粒间微观内部力链网络 Fig.2　Microscopic network of internal force chainamong sand particles under the action of gravity

砂土是典型的颗粒物质，在颗粒间相互作用下形成一个复杂的体系。近年来对于颗粒物质的研究倾向于精细力学行为方面，并进行了大量的试验观测与数值仿真试验，但至今对于颗粒体系中的静力和动力学行为仍无法用经典固体、流体力学解释清楚。从细观角度看，散体颗粒是由不同级配的颗粒组成的多空隙结构，砂土颗粒尺度上的细观结构构成，见图3。

科学研究的对象要从最小的特征结构单元入手[19-20]，对于砂土以砂粒团簇单元为研究对象，通过构建由新旧元件及其组合的简化力学模型来描述颗粒间的细观力学行为。选取饱水砂土的最小特征结构单元，从细观角度对单粒砂进行受力分析(见图4)。由图4可见，单粒砂主要受重力G,水中浮力Fb，法向接触力Fn，切向接触力Ft和渗透力Fsep作用。

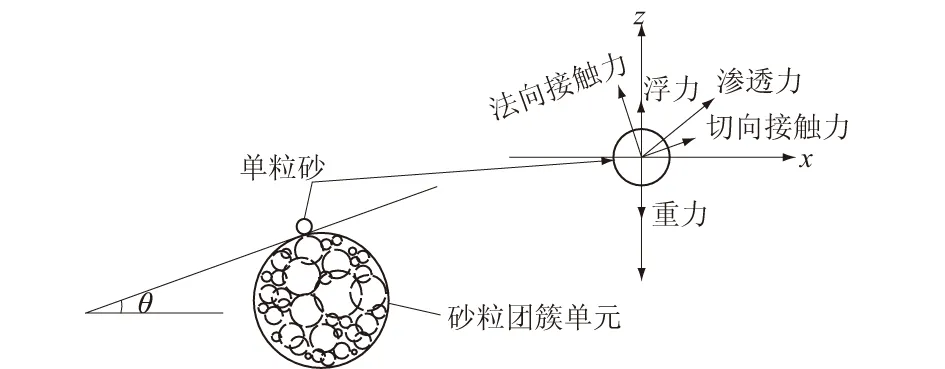
图4　水中砂粒团簇特征结构单元受力分析Fig.4　Force analysis for characteristic structure unit ofsand clusters in water

对于砂粒体系中的力链通常可承受一定的切向力作用。一般力链不长，大约为10倍砂粒粒径，颗粒物质与以空间尺度为主的固体介质有明显区别。

3.2　砂土蠕变模型及改进

对于工程中的散体颗粒研究对象，如泥石流、无黏性土、黏性土、砂砾、石等，特征结构单元间存在强力链的连接。在一定条件下，当强力链在外力作用下达到内力极限时，强力链即会被打断。在渗流作用下，散体颗粒由固态弹塑性变形状态转化为固-液2相的变形状态，而从细观角度来看，该过程均是从散体颗粒的特征结构单元的起动、运移开始的一个渐进过程。在砂土颗粒间发生缓慢移动变形的过程中，出现砂粒特征结构单元从砂粒团簇中剥离的现象。抗剪强度几乎为0，处于“悬浮”的起动临界状态，而从细观角度来看，颗粒间的强力链相当于宏观上的虚拟杆单元。可考虑引入塑性铰的概念，描述强力链上发生塑性滑动，形成塑性铰，发生平移、转动的运动过程。

А.Я.Будин在文献[21]中，尝试用弹性、塑性、黏性元件和某些非线性变形的结构元件，建立反映土变形时结构变化过程的Будин模型，见图5(a)。图5(a)中，θnp为结构元件的转动角度，SV1为“塑转铰”元件，SV2为滑片元件，N为黏壶元件。

Будин模型中的塑性滑片元件无法实现转动，而当进入滑动阶段后，对塑性发展区引入结构力学中的塑性铰可描述塑性区域形成后的转动，在塑性铰处的弯矩趋于0，而铰的位置上仅存在可向x,y这2个方向上分解的力。可通过“塑转铰”元件取代传统塑性滑片元件来描述岩土颗粒间的转动状态，对Будин模型进行改进，更加真实地反映土体颗粒间移动变形过程，如图5(b)所示。

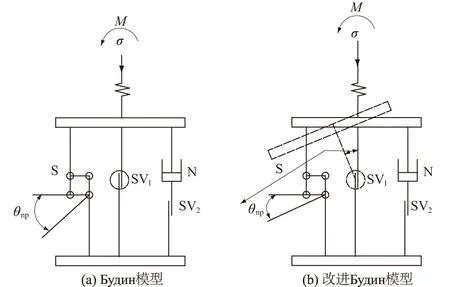
图5　Будин模型和基于“塑转铰”的改进Будин模型Fig.5　Будин model and improved Будин modelbased on “plastic-to-hinge” element

“塑转铰”元件能反映土体变形过程中颗粒间发生转动的过程，从而相应地改变变形速度。颗粒方向变化用“塑转铰”元件来模拟。黏性元件服从的关系式为

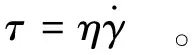
(1)

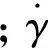
而“塑转铰”元件的剪应变可用式(2)的非线性关系式来描述，即

γs=γ*tan(τstηs-1)。

(2)

式中：γs为“塑转铰”元件的剪应变；γ*为结构元件的剪应变，且γ*=γP/sinθs，γP为结构完全重新分布时的剪应变；θs为结构单元S转动的极限角；τs为结构元件剪应力；t为蠕变时间；ηs为黏性元件黏度。

模型剪应变及模型剪应力强度的表达式分别为:

γ=γs+γN,

(3)

τ=τs=τN。

(4)

式中：γ为模型剪应变；γN为黏性元件剪应变；τs为结构元件剪应力;τN为黏性元件剪应力。

模型方程可由式(3)和式(4)推导而得。τT(1)为“塑转铰”元件的极限抗剪强度。当τ<τT(1)时，不发生蠕变；当τ≥τT(1)时，发生与土颗粒重新定向有关的衰减蠕变，即

(5)

式中τT1为“塑转铰”元件的极限抗剪强度。当θ=θnp时，颗粒重新定向停止，进一步的变形可能是稳定流动，即

(6)

式中τT2为滑片元件SV2的极限抗剪强度。稳定流动的发生条件为τT(1)<τ<τT(1)+τT(2)。

3.3　砂土蠕变曲线及流变状态方程

文献[21]给出最原始的蠕变曲线微分方程为

(7)

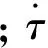
线性黏弹性状态方程的一般形式为

(8)

式中α0,α1,α2,β1，β2均为系数。

当τ为常数时，式(7)的解为

(9)

对于卸载情况，即τ=0时，式(7)的解为

(10)

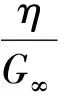
τ=Gγ+G0-Gγexp(-t/Tr)=

τ-τ-τ0exp(-t/Tr)。

(11)

式中：τ为长期剪切强度；τ0为瞬时剪切强度。

因此，式(7)可描述土体弹性后效、松弛过程，同时考虑了瞬时变形。应力松弛过程可描述极限应力达到某个终值，而不是0，因此式(7)可用以描述综合性弹黏性体的流变状态方程。

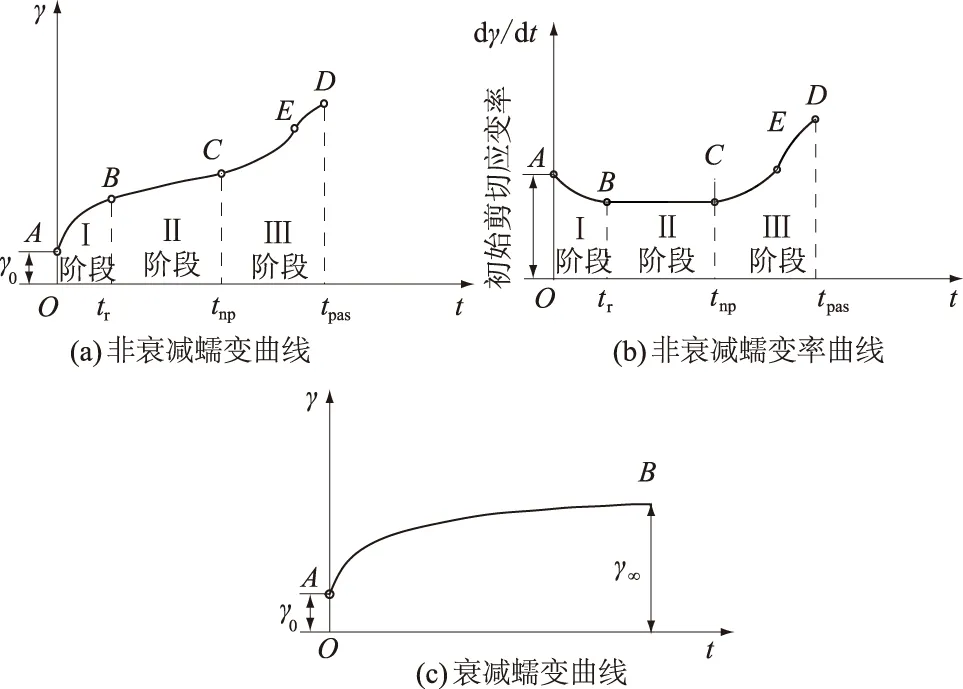
图6　根据蠕变发展趋势的蠕变分类Fig.6　Creep classification according to creepdevelopment tendency

蠕变过程按发展趋势可分为非衰减蠕变(见图6(a))、非衰减蠕变率蠕变(图6(b))、衰减蠕变(图6(c))。非衰减蠕变曲线可分为3个阶段。tr,tnp,tpas分别为第Ⅰ阶段、第Ⅱ阶段、第Ⅲ阶段终了时刻。变形均等于受荷载后立即发生的相对瞬时变形与随时间发展的变形2部分之和,即

γ=γ0+γt。

(12)

在非衰减蠕变曲线及蠕变率曲线的第Ⅲ阶段，存在一个加速度为正的加速蠕变阶段CE，还存在一个加速度为负的加速蠕变阶段ED。对于砂土在非衰减蠕变的第Ⅲ阶段中的此类蠕变特性，经分析是由于砂粒间接触摩擦和变形移动所致。由于改进Будин模型引入“塑转铰”元件，可以较好地描述非衰减蠕变中的第Ⅲ阶段加速蠕变的过程。

4　模型辨识

为验证改进Будин模型的可靠性和有效性，自行研制模型试验装置进行动水携砂试验，并将试验结果与文献[22]试验数据进行对比。

4.1　动水携砂试验

为模拟不同水力梯度下动水携砂过程，观测砂层在自重应力及水力梯度作用下的剪切变形特征及砂层内部破坏形态，自主研发动水携砂模型试验装置，试验模型箱采用透明玻璃材质制作，见图7。

图7　动水携砂模型试验装置Fig.7　Model test apparatus for moving water and sand

首先清洗干净模型，将模型下端的圆孔堵住。然后分别在5个模型槽内注入0，11.5，13.0，14.5，16.0 cm高的水; 然后在各个玻璃槽中分别加入质量均为10 kg，含水率为0的干砂，铺砂厚度26.0 cm；静置一段时间，让水与砂混合均匀，然后把小孔中的各个塞子同时拔开。在各个槽下端的小孔处放置一个烧杯，收集从孔中携出的水-砂混合物；待每个槽中的水-砂混合物不再漏出。通过观测发现砂层内部出现了“阶梯状”的分层现象(图8(a))。

从上向下测量以上各个玻璃槽中“阶梯”的高度，测量方法是取2根细长线，然后分别在2根细长线一端放置一枚针，并分别将另一端都绑在一根直杆上，然后移动细线测出“阶梯”的高度,见图8(b)。

图8　“阶梯状”的分层现象及“阶梯”高度的测量Fig.8　Ladder-like layered phenomenon andmeasurement of ladder height

不同注水高度下 “阶梯”自重应力方向剪切应变随时间的变化曲线见图9，汇总结果见表1。

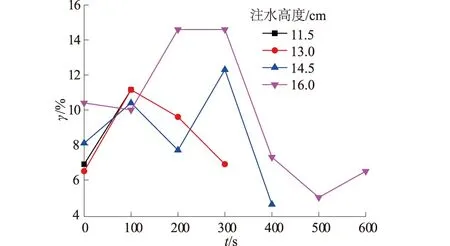
图9　不同注水高度下 “阶梯”自重应力方向剪切应变随时间的变化曲线Fig.9　Shear strain in self-weight stress direction ofladder against time under different water injection heights

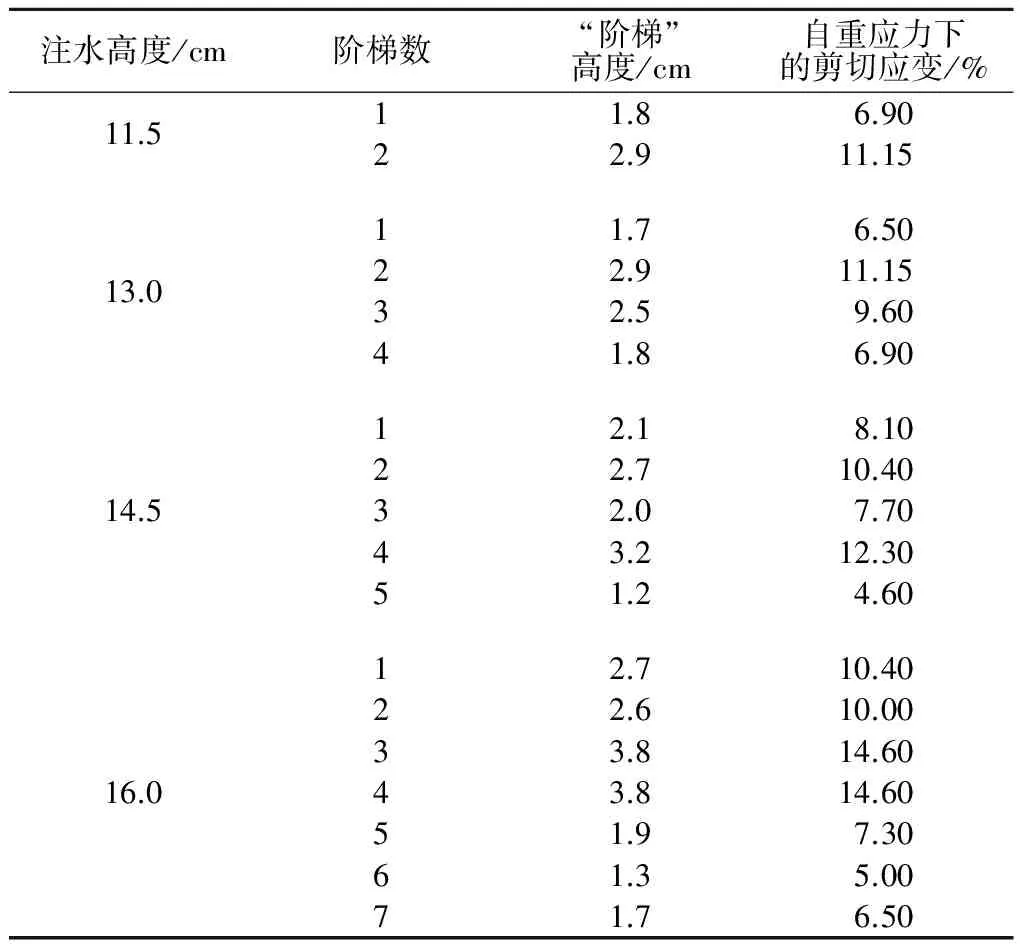
注水高度/cm阶梯数“阶梯”高度/cm自重应力下的剪切应变/%11．513．014．516．011．86．9022．911．1511．76．5022．911．1532．59．6041．86．9012．18．1022．710．4032．07．7043．212．3051．24．6012．710．4022．610．0033．814．6043．814．6051．97．3061．35．0071．76．50

图9和表1反映了不同注水高度条件下，砂层在自重应力水平下的沿着垂直方向的剪切应变均为一个衰减过程，最大剪应变水平在10%～15%附近出现屈服平台，而动水携砂过程显著缩短了砂土颗粒间的剪切蠕变时间。

4.2　砂土剪切蠕变试验

为了验证文中蠕变模型的合理性,选取文献[22]剪切蠕变试验中，在正应力P=2.5 MPa时细砂试件在恒定剪切荷载下的蠕变曲线,见图10。

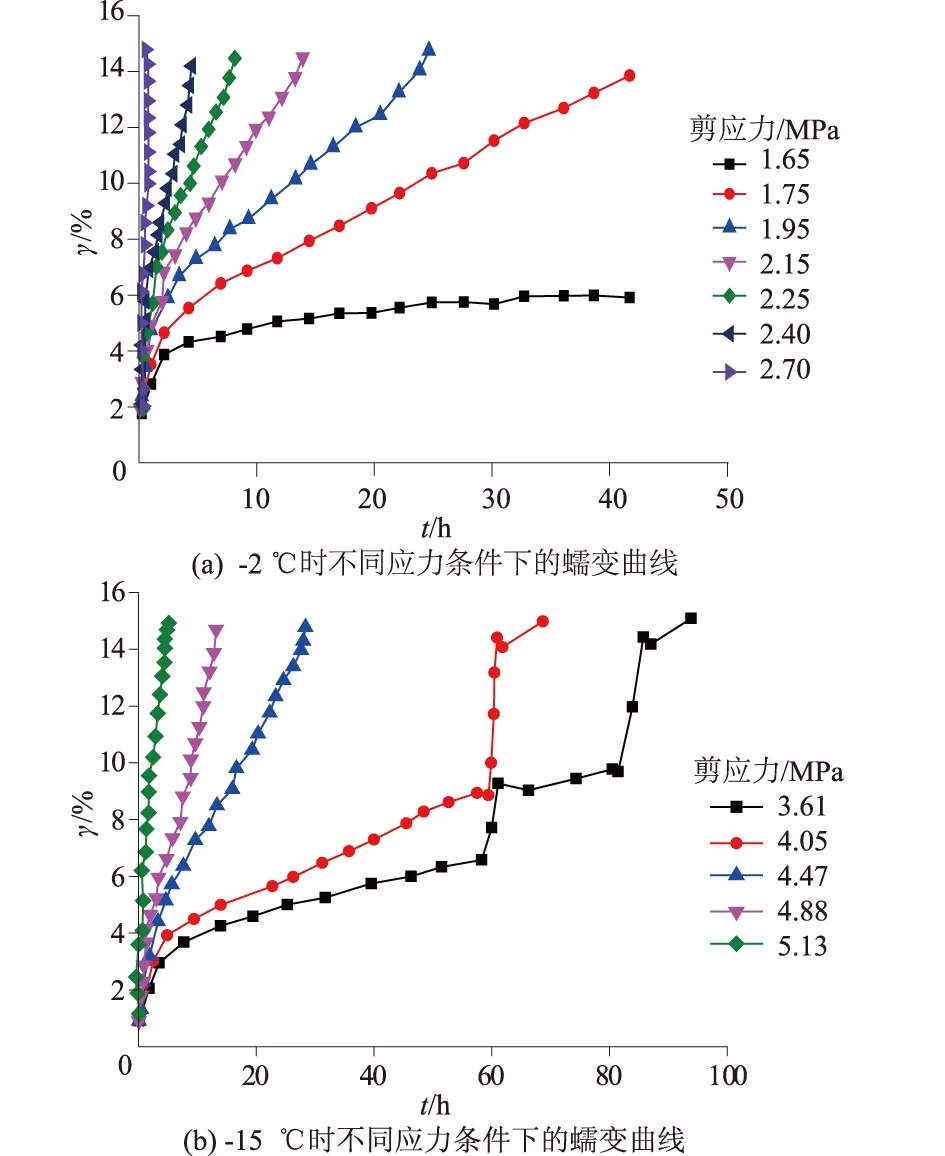
图10　文献[22]蠕变试验结果Fig.10　Creep test results from reference [22]

从图10可以看出，当温度降至-15 ℃以下时，在低应力条件下的蠕变曲线的3个阶段较明显，而温度在-2 ℃时，与-15 ℃时的蠕变曲线形态区别显著；当温度处于-15 ℃时，在低应力条件在出现了2次塑性屈服后进入加速蠕变至破坏。试验结果与图6(c)中的规律较接近，证明了在第Ⅲ阶段加速蠕变过程中存在着正加速度和负加速度加速蠕变，正加速度蠕变使土体变形加速趋近变形和强度极限，而负加速度加速蠕变使土体加速变形趋势减缓，使屈服极限出现滞后现象，经分析得到该蠕变阶段是造成冻结砂土蠕变的直接原因。

在-15 ℃温度，剪应力为3.61 MPa的低应力水平下，试验蠕变曲线较接近2.3节分析的第Ⅲ阶段蠕变曲线形态，因此采用该试验数据进行拟合和模型参数辨识，结合Levenberg-Marquardt(LM) 与通用全局优化算法(Universal Global Optimization,UGO)进行拟合与参数辨识，模型参数与拟合结果见表2。拟合结果显示改进Будин模型拟合相关度较好。

4.3　砂土剪切蠕变试验与动水携砂模型试验对比

通过对比图9与图10(b)的剪应变曲线，可发现文献[22]的试验结果与本文试验结果中的剪应变均在10%～15%附近出现屈服平台，均为衰减过程，动水携砂试验中在高水头差作用下，虽然自重应力水平较低，但在沿着垂直方向的剪切力作用下，在较短时间内即达到剪应变极限，且剪应变水平与文献[22]剪切蠕变试验的应变水平接近，验证了改进Будин模型的可靠性和有效性。

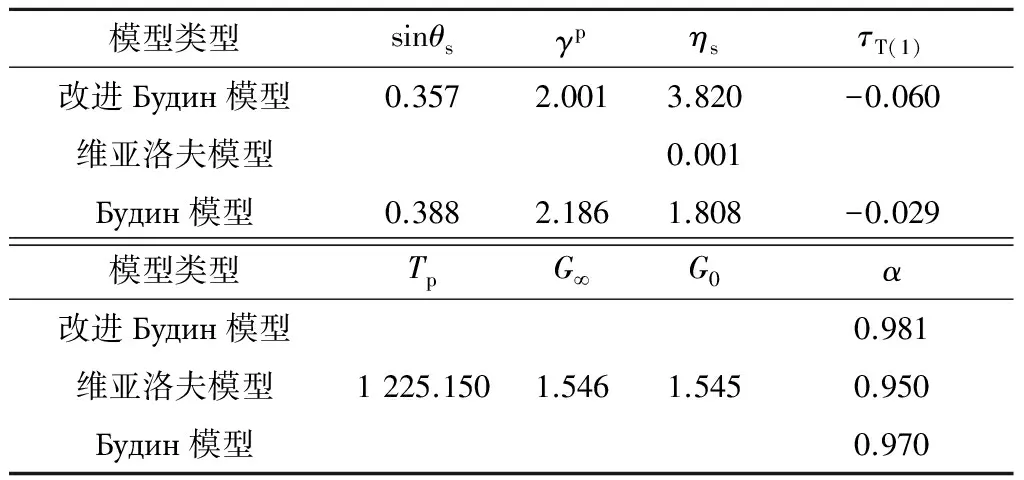
表2　模型参数辨识成果Table 2　Identification data of model parameters

注：α为拟合相关度

5　结　论

(1)提出一种新的 “塑转铰”元件，对滑片元件进行改进，可描述材料颗粒间发生塑性滑动后的转动过程。

(2)基于“塑转铰”元件对Будин模型进行改进，并给出其本构方程和蠕变曲线方程，可较好地揭示第Ⅲ阶段蠕变过程中，由于砂粒间的挤压、接触摩擦形成塑性滑动、转动区域的正加速度和负加速度蠕变过程。

(3)通过动水携砂模型试验及砂土蠕变试验数据对改进Будин模型进行了模型验证与参数辨识，结果表明该模型精度较好，从而为分析露天矿复合边坡松散砂层内砂土颗粒间的蠕变机理提供了一种新的蠕变力学模型。

参考文献：

[1]武强，崔芳鹏，赵苏启，等. 矿井水害类型划分及主要特征分析[J]. 煤炭学报, 2013, 38(4): 561-565.

[2]汪闻韶.土的液化机理[J]. 水利学报,1981,(5):22-34.

[3]BARDET J P, KAPUSKAR M. Liquefaction Sand Boils in San Francisco During 1989 Loma Prieta Earthquake [J]. Journal of Geotechnical Engineering，1993， 119(3)：534-562.

[4]HOLZER T L, CLARK M M. Sand Boils Without Earthquakes[J]. Geology, 1993,21(10):873-876.

[5]CASAGRANDE A. Liquefaction and Cyclic Deformation of Sands—A Critical Review[C]∥Harvard Soil Mechanics. Proceedings of the 5th Pan American Conference on Soil Mechanics and Foundation Engineering.Buenos Aires，Argentina，November 17-22，1975:80-133.

[6]邓荣贵，张倬元，刘宏.饱和砂土动力液化到渗流液化过程探讨[J]. 山地学报, 2001, 19(5): 430-435.

[7]刘红军，李洪江，王虎，等.饱和海床土渗流-应力耦合损伤及液化破坏规律(Ⅰ)[J]. 哈尔滨工程大学学报, 2014, 35(11): 1-7.

[8]李洪江，刘红军，王虎，等.饱和海床土渗流-应力耦合损伤及液化破坏规律(Ⅱ)[J]. 哈尔滨工程大学学报, 2014, 35(12): 1480-1486.

[9]周健，姚志雄，张刚.砂土渗流过程的细观数值模拟[J]. 岩土工程学报, 2007, 29(7): 977-981.

[10] 李广信，周晓杰.堤基管涌发生发展过程的试验模拟[J]. 水利水电科技进展, 2005, 25(6): 21-24.

[11] 刘忠玉，乐金朝，苗天德.无粘性土中管涌的毛管模型及其应用[J]. 岩石力学与工程学报, 2004, 23(22): 3871-3876.

[12] 李守德，徐红娟，田军.均质土坝管涌发展过程的渗流场空间形状研究[J]. 岩土力学, 2005, 26(12): 2001-2004.

[13] 刘丹珠，张家发，李少龙，等. 考虑土体坍塌的单层堤基管涌数值模拟方法研究[J]. 长江科学院院报, 2012, 29(10): 98-101.

[14] 隋旺华，蔡光桃，董青红.近松散层采煤覆岩采动裂缝水砂突涌临界水力坡度试验[J]. 岩石力学与工程学报, 2007, 26(10): 2084-2091.

[15] 隋旺华，董青红.近松散层开采孔隙水压力变化及其对水砂突涌的前兆意义[J]. 岩石力学与工程学报, 2008, 27(9): 1908-1916.

[16] 杨伟峰.薄基岩采动破断及其诱发水砂混合流运移特征[D]. 徐州：中国矿业大学, 2009.

[17] 孙其诚，王光谦.颗粒物质力学导论[M]. 北京：科学出版社，2009.