黄河冲积互层深基坑围护桩插入比优化分析

2018-04-17，,，，，

长江科学院院报 2018年4期

　，, ，，，　

(1.山东科技大学土木工程与建筑学院，山东青岛　266590； 2.济南轨道交通集团有限公司，济南　250101)

1　研究背景

黄河“水少沙多、水沙异源”，历史上多次改道留下了厚冲积土层，形成了大面积冲积平原。上游多为砂卵石层，中游多为砂粉质土层，下游多为黏性土层，且多有夹层及互层，竖向异性。砂卵石层中含水量丰富，砂粉质土有液化倾向，黏性土塑性较高。以济南地区为例，该地区处于鲁西南低丘平原、鲁西北黄泛平原和鲁中的山前冲积平原三者的过渡地带上，地基土层属第四系，土层重度随深度增加，下部土层较密实，渗透系数较小，液性指数在0.2～0.8之间，处于硬塑或可塑状态，土体压缩模量随深度增加变化较小。研究黄河厚冲积地层岩土体的物理力学特性，深入分析该地区深基坑变形特征，对设计施工及后续的维护等具有重要的指导意义和实践意义。

国内外学者均对深基坑插入比及黄河厚冲积平原深基坑稳定性进行了研究，Poh等[1]利用EXCAV有限元软件研究了插入比对桩墙水平位移和桩弯矩的影响；高新南等[2]利用深基坑变形分析软件研究了在渗流稳定作用下围护桩的变形规律，定量确定了苏州地区深基坑围护桩插入比取值；李淑等[3]、杨将等[4]对北京地区围护结构插入比进行研究，得出深基坑地表沉降与插入比大小成反比，围护结构入土深度应控制在(1.2～1.4)h(h为基坑深度)之间；陈斌等[5]通过对监测数据进行分析，得出围护桩开挖深度与围护桩的刚度成反比，桩位变化曲线呈线性变化；武朝军等[6]通过对比上海地区地层条件，得出苏州地铁车站在插入比为0.86下深基坑围护结构的最大侧向位移约为0.16%H，墙后最大地表沉降值约为0.13%H；李四维等[7]利用数值模拟与监测数据进行对比，得出基坑桩体的嵌固深度在一定范围内每增加1 m，基坑变形比减小1倍；徐飞等[8]分析了黄河冲积平原地区超大型深基坑在特定插入比下结构变形规律。但在这些研究中，未对黄河厚冲积层地区深基坑插入比影响深入研究，土层质量系数和土压力折减系数的选取也没有具体体现。

本文在前人研究的基础上，借助数值计算软件FLAC3D和理论分析细化插入比的取值范围，以山东省文化艺术中心深基坑实测数据为例，研究深基坑在开挖过程中围护桩侧向位移、沉降以及锚索轴力的变化特征，旨在优化桩体的插入比，为该地区开挖支护设计计算与施工提供参考。

2　插入比分析与理论计算

桩体插入比λ是指基坑支护工程中，竖向围护结构在基坑底面以下长度与基坑底面以上长度之比,即

λ=(L-H)/H。

(1)

式中：L为竖向围护桩的长度；H为基坑底面以上桩体的长度。

插入比过小时，对抗倾覆稳定性、基坑底抗隆起稳定性影响较大，基坑变形过大导致失稳，且影响跨度较大的基坑抗浮稳定参数值，进而产生渗流和底鼓等现象；插入比过大时，桩和基坑的稳定性不会随插入比的增大明显变化，反而会增加工程造价，延长施工工期。因此，基坑施工过程中，必须确定合适的插入比才能实现工程安全和经济的共赢。

2.1　土层质量对插入比的影响

黄河厚冲积层地质条件好，地层参数较高，为河流相多元冲积结构，主要特点是微欠固结，成层性和孔隙承压水，土体相对稳定。考虑黏聚力和内摩擦角均值下的土层质量参数Φ为

(2)

其中：

(3)

(4)

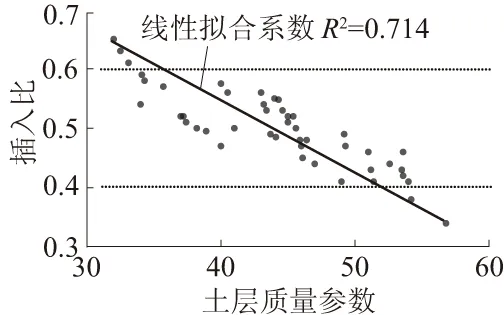
图1　土层质量参数与插入比关系Fig.1　Relationship betweenquality index of soil layerand pile insertion ratio

将式(3)、式(4)代入式(2)得到土层质量参数为

(5)

插入比λ与土层质量参数Φ关系式为

λ=-0.012 7Φ+1.376。

(6)

将式(5)代入式(6)可得

(7)

分析发现：深基坑的土层质量参数与基坑支护结构的插入比存在某种特定联系。现调取34组无特殊条件的围护排桩支护结构和12组地连墙支护结构作为统计对象，探讨支护结构插入比与土层质量参数之间的关系，如图1所示。

由图1可以看出，围护桩的插入比与土层质量参数成反比，且线性拟合系数R2=0.714，与式(6)所得结果一致，土层质量越好，插入比越小，符合常理。针对黄河厚冲积层地区，深基坑插入比设计计算中要充分考虑土层质量参数的影响，合理利用其对桩体的作用效果。

图1中2条水平虚线分别表示插入比为0.4和0.6，统计数据中，超过85%位于这2条虚线之间，由此得出围护排桩支护和地连墙支护的插入比取值区间大致在0.4～0.6之间。盲目增加桩体插入比，不仅增加工程造价，也使施工难度大大提高[9]，因此必须依托土层质量的研究结果，提高桩体的利用率。针对济南特殊地层条件下桩体插入比的最优计算方案，以下作了详细分析。

2.2　最优插入比计算

图2　基坑结构受力简图Fig.2　Forces acting onfoundation pit structure

围护桩的插入比是决定深基坑稳定性和经济性的关键参数。围护桩合适的入土深度不仅关系到基坑的稳定性，更是关乎结构整体的可靠度。基坑结构计算简图如图2所示，图中:F1，F2，F3分别为基坑所受锚索、钢支撑、混凝土支撑作用力;H为基坑深度;q为地面均布荷载;C点为基坑下部深入土体的围护桩在受力作用下的反弯点;RC为反弯点作用力;h5为反弯点深度;h6为反弯点距桩底深度。

2.2.1引入土压力折减系数μ

入土深度的假定系数试算是处理技术问题的一种方法，然而得到的结果仍然有一定程度的近似。本文作了直接简化，并尝试提出计算方法。由于主动土压力、被动土压力不可能完全发挥，即发挥度不会永远等于100%，所以在围护桩的计算时，土压力需折减处理，假设土压力折减系数为μ。根据文献[10-11]以及《建筑结构荷载规范》(GB 50009—2012)[12]第2.2.6条附注“对抗倾覆和抗滑移有用的永久荷载，其土压力的分项折减系数可取0.9”，结合研究的护坡桩所承受的永久荷载得到土压力的荷载分项系数有2种情况：①主动土压力折减系数取1.2；②被动土压力折减系数取0.9。

2.2.2单支撑或单锚围护桩入土深度计算

为了便于分析与计算作出如下假设：基坑土为砂砾，黏聚力C=0，各支撑处为铰支连接。则朗肯主动土压力系数为

Ka=tan2(45°-φ/2)。

(8)

式中φ为填土的内摩擦角(°)。

折减后的朗肯主动土压力系数为

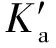
(9)

朗肯被动土压力系数为

Kp=tan2(45°+φ/2)。

(10)

折减后的朗肯被动土压力系数为

(11)

此处引入相关系数η为

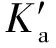
(12)

其中：

α=h1/H；β=q/(γH)；

λ=x/H；x=h5+h6。

式中：λ为围护桩的插入比；h1为第1个支撑到桩顶的距离；γ为土的重度；x为围护桩的入土深度；α，β为引入常数。

当围护桩横撑设在桩顶(即h1=0)时，式(12)可简化为

(13)

同时结合黄河冲积平原地区深基坑插入比相关经验，得到插入比λ的参考取值，如表1所示。

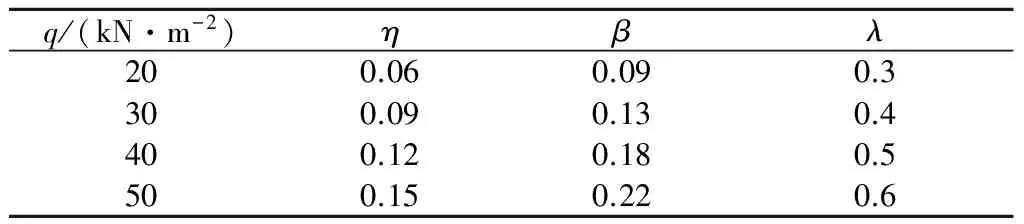
表1　围护桩插入比的参考取值Table 1　Reference values of insertion ratio ofsupporting pile

参考表1,对于济南地区黄河厚冲积层地区单支撑或单锚支护基坑的插入比分析，可直接由地层参数和地表均布荷载确定插入比取值区间。

2.2.3应用等值梁法计算围护桩的入土深度

国内学者陆培毅等[13]通过对被动区土弹簧抗力引进弹塑性假设，解决了利用弹性抗力法计算支护结构插入深度问题，但其在计算过程中安全系数的确定还不够完善，而且计算方法局限性比较大。为了更准确地确定入土深度，在此引入等值梁法计算方法，将计算插入比与表1以及后续模拟结果对比，使结果最优。

首先，应用等值梁法计算插入比，围护桩弯矩为0的点假设为铰点支座，利用土压力强度为0处(即点C)与弯矩为0处接近重合的原理，把该点视为理想铰点，则点C距离基坑底的距离为

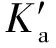
(14)

由式(14)可求出点C到基坑底的距离h5，可视桩(H+h5)段为一简支梁，如图3所示。

图3　结构简支梁简化模型Fig.3　Simplified model of the structuralsimply-supported beam

图3中点C的支座反力RC可认为与CD段的土压力等效，即可根据图3的CD段求得RC为

(15)

由式(15)可以求出围护桩h6，其计算式为

(16)

当地面的均布荷载为0或者很小可以忽略(即q=0)时，式(16)可简化为

(17)

联立式(15)和式(17)可求出桩入土深度。

其次，利用等值梁法计算围护桩的入土深度，支座反力RC和CD段桩前土压力对围护桩桩底D点力矩相等，当q=0时，可得

(18)

围护桩的入土深度为

(19)

2.2.4多支撑或多锚支护围护桩入土深度计算

对于多支撑或多锚支护的围护桩插入比的计算，当桩前和桩后土压力分布符合假设要求时也可采用等值梁法计算，按简化连续梁模型计算支座反力RC，进而求得桩的插入比，此处对其不再赘述。

3　工程概况

山东省文化艺术中心工程地处黄河及小清河冲积形成的平原地带，为典型的黄河厚冲积黏土地层。水文地质单元位于西郊玉符河隐伏冲积扇前缘砂、砾石富水区，地下水类型为第四系孔隙潜水地层，综合渗透系数可取k=16.5 m/d，场地静止水位埋深3.95～5.55 m，详勘阶段地下动水位标高15.47～19.20 m。钻探揭示地层上部为黄河、小清河冲积成因的黏性土、粉土等，下部为山前冲洪积成因的黏性土、砂土、卵石土，局部含砂层。基坑支护土体各土层参数如表2所示。

表2　基坑支护土体各土层主要物理力学参数Table 2　Physical and mechanical parameters of each soil layer of the foundation pit

基坑开挖按一个整体基坑考虑，基坑开挖范围271 m×192 m(长×宽)，挖深H为18.7 m。考虑基坑的稳定性、安全性及经济性问题，基坑-7.2 m以上按1∶0.8放坡开挖，并设置3道土钉，土钉长度分别为9，6，6 m，土钉与水平面的夹角为5°，挂网喷混凝土；-7.2 m以下采用单排桩支护，围护桩桩长为22.3 m，直径为0.8 m，桩间距为1.5 m，桩顶设置1 m×0.8 m(长×宽)的压顶冠梁以提高基坑整体稳定性；桩身设置3条不同长度锚索，从上往下长度依次为25，28，25 m，锚索间距依次为4.0，4.0，3.5 m，锚索与水平面的夹角为15°，如图4所示。

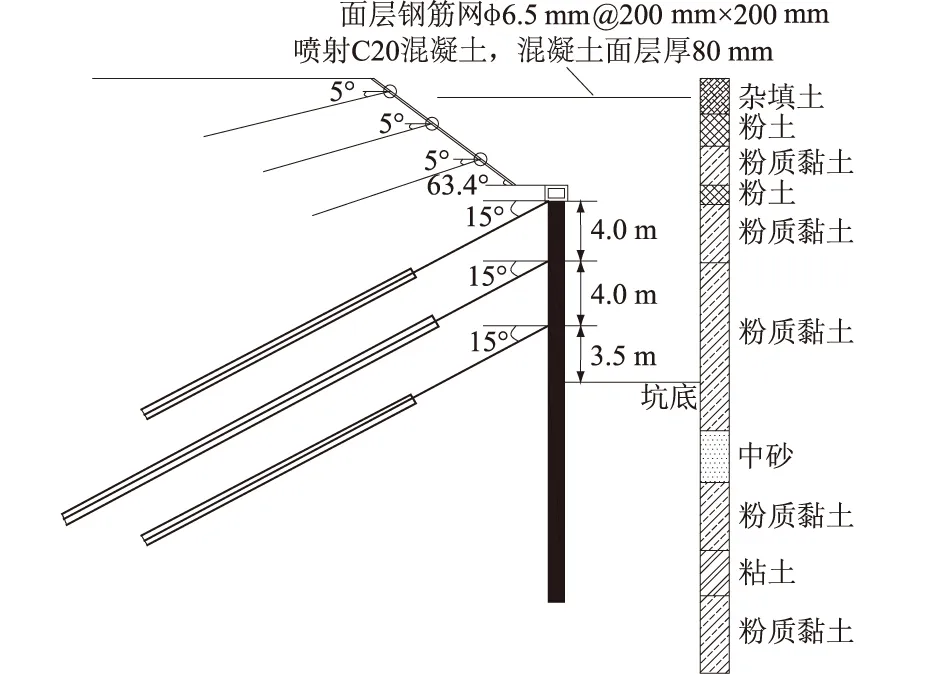
图4　支护结构和地层概况简图Fig.4　Sketch of support structure and soil strata

图5　三维计算模型示意图Fig.5　Schematic diagramof the 3D model

4　数值模拟分析

4.1　计算模型

根据对称性，基坑三维计算模型取实际基坑一半进行模拟，如图5所示。本构模型采用Mohr-Coulomb模型，地层物理力学参数参考地质勘察资料提供的固结快剪试验指标，将模型概化分成9层，通过现场单桩堆载试验数据，以0.98的逼近率反演优化地层参数。围护桩桩体采用实体单元，土钉与锚索均采用Cable单元，根据其挠度和屈服强度选取参数。

4.2　数值模拟过程

(1)初始应力场的确定。

(2)按照1∶0.8放坡开挖并进行土钉墙施工，开挖到-7.2 m处。

(3)开挖第1层土体，施工指定插入比下的围护桩和压顶冠梁，设定监测点，并施加第1道预应力锚索(25 m)，开挖至-11.2 m处。

(4)开挖第2层土体，施加第2道预应力锚索(28 m)，开挖至-15.2 m处。

(5)开挖第3层土体，并施加第3道预应力锚索(25 m)，开挖至-18.7 m处，即坑底。

(6)调取模拟数据，对其进行分析研究。

(7)变换插入比，重复步骤。

4.3　数值计算结果及分析

由上文统计可知：根据土层质量确定的黄河厚冲积层插入比范围为0.4～0.6。为了更清晰地分析插入比变化对基坑内力和整体变形规律，模拟时设定插入比范围为0.3～0.8，步长为0.1，在插入比0.4～0.7之间加密3次，具体计算方案如表3所示。

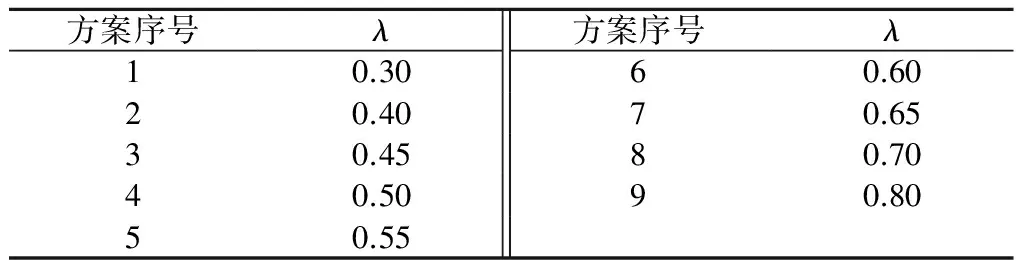
表3　模拟方案Table 3　Simulation schemes

4.3.1插入比对稳定性参数影响

以水平位移为标准判定围护桩的稳定状态。图6(a)所示为数值计算过程中围护桩最大侧向位移随插入比的变化趋势，显然增加插入比可以有效地减小桩体的侧向位移。计算结果显示：当插入比<0.4时，桩体最大侧向位移受插入比影响明显；当插入比为[0.3, 0.4)时，桩体最大侧向位移减小幅度为6 mm；当插入比为[0.4,0.55)时，侧向位移降幅为2.4 mm；而当插入比增加到0.6时，继续增大插入比几乎对桩体最大侧向位移无影响，说明此时已满足支护结构的稳定性要求，继续增加插入比(0.6～0.8)，最大侧向位移的减小幅度仅为0.7 mm，对控制支护结构变形效果并不明显，反而会增加工程造价和施工难度。以上研究结果与高夕良[14]、王国富等[15]通过理论计算的方法得到的规律相似。支护结构侧向位移并不随插入比的增大而无限制地减小，当插入比达到一定值时，企图通过增加插入比减小侧向位移是不可取的。

基坑稳定性的另一个重要参数指标为地表沉降，桩前土体的开挖导致基坑应力重新分布产生新的平衡，放大效果即为桩体的变形导致的地面沉陷。图6(b)所示为基坑地表最大沉降量随插入比的变化规律。当插入比为[0.3,0.4)时，降幅为6 mm，而当插入比为[0.4,0.55)时，降幅仅为2.1 mm。此后，沉降变化趋势并不明显，地表沉降随插入比的变化规律同侧向位移随插入比的变化规律相同。

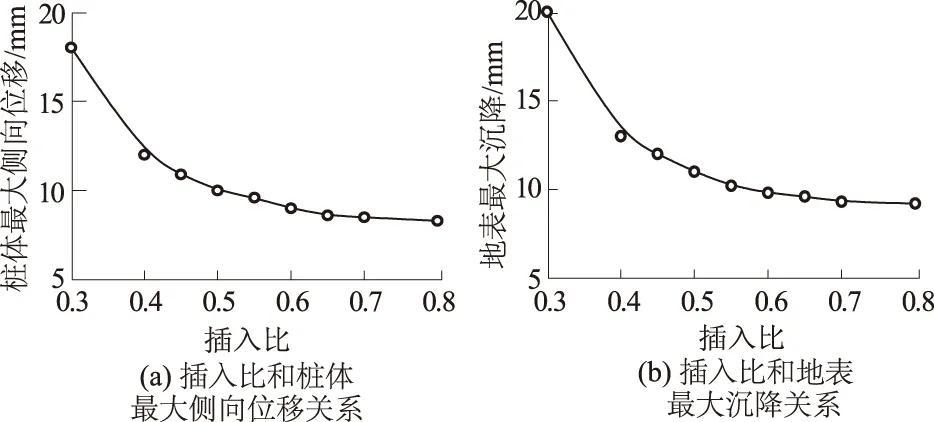
图6　插入比与桩体最大侧向位移量和地表最大沉降量之间的关系Fig.6　Variation of maximum lateral displacement andmaximum subsidence of ground surface againstinsertion ratio of pile

由图6也可得出，当插入比<0.4时，基坑变形较大，这是因为：①入土深度小导致反弯点距离基坑底过小；②基坑-7.4～-12.9 m深度范围内土层为中砂和粉质黏土，而中砂和粉质黏土呈软塑-流塑状态，流塑性增大就会导致侧压系数增加，继而导致侧压力增大。工程实例中基坑实际插入比为0.58，桩端持力层为第⑥层黏土，土层塑性指数Ip1>17，上部粉质黏土塑性指数100.55后优化效果不明显。因为计算模型中未考虑水位及渗流对基坑变形的影响，所以导致图6中模拟计算结果高出预估值。

4.3.2模拟变形云图对比

通过对9种不同方案的数值模拟计算，选取最有代表性的方案1、方案2、方案5、方案6进行展示(各方案插入比分别为0.30，0.40，0.55，0.60)，如图7所示。各方案下变形最大处均发生在基坑顶部，随后沿应力弧由上及下扩散，变形逐渐减小。图7(a)云图中变形最大，最大值达20.3 mm；其次为图7(b)，最大值达15.3 mm；图7(c)中变形最大值为10.2 mm;图7(d)中变形最大值为0.1 mm,与图7(c)很接近。由此可见当插入比为在0.40和0.55时基坑抗倾覆稳定性与抗底鼓稳定性已基本达到要求。基于以上4种方案差异可知：①方案1中围护桩入土深度太小，违背了基坑可靠度准则；②则与其桩端持力层性质有关，方案1桩端位于中密(稍湿)的中砂层，方案2桩端位于粉质黏土层，方案5中土层为硬塑状态的黏土，土层重度、密实度与深度存在正比关系，与理论计算结果吻合。

图7　4种插入比模拟变形云图对比Fig.7　Contours of simulated displacement in thefoundation pit with four insertion ratios

4.3.32种方案与实测结果对比分析

对比插入比分别为0.55和0.40下的数值模拟方案与理论计算方案，并利用实测数据加以验证，如图8所示。由图中数据对比可知：计算方案(插入比为0.40)下累计沉降位移最大值为7.8 mm，相对实测增大了11.4%；模拟方案(插入比为0.55)最大累计位移7.5 mm，相对实测增大了7.1%。2种优化方案与实测数据(插入比为0.58)下地表沉降累计位移相差不大，而2种方案的插入比却优化了将近一半，故由此得出实际方案中桩体插入比设计不合理，原因可能是设计中未考虑地层条件(土层质量)对桩底的作用效果。

图8　2种方案与实测数据的沉降累计位移对比Fig.8　Comparison between cumulative displacements intwo schemes and measured data

5　插入比实测结果验证

以上对插入比优化进行了理论计算和数值模拟，但所得结果还需实测数据来对比分析。以山东省文化中心深基坑现场监测数据为例，该深基坑围护桩插入比为0.61，现调取该深基坑桩体水平位移、竖向位移、锚索轴力随时间增长的累计变化值作为参考。

5.1　桩体水平位移

5.1.1桩顶水平位移

基坑支护桩顶的冠梁上布设测点，利用实测数据得出各围护桩桩体的水平位移随开挖进度(时间)的变化趋势，如图9所示。

图9　围护桩桩顶水平位移Fig.9　Horizontal displacement at the top of supporting pile

如图9所示，10#桩桩顶水平位移出现负值，即桩顶向基坑外部移动，是由于该桩体位于基坑的阳角处，但位移较小，仅为2.5 mm(约0.013%H)。其他测点处水平位移最大值为8.1 mm(约0.04%H)，未超过桩顶水平位移报警值(0.1%H)，且距报警值相差较大。

5.1.2深层水平位移

由于10#和11#桩未安装测斜管，因此,只调取1#,2#,3#桩测斜数据分析。由图10测斜数据可知，1#桩深层水平位移最大值为10.7 mm；2#桩深层水平位移最大值为14.2 mm；3#桩深层水平位移最大值为16.6 mm；最大深层水平位移范围在(0.06%～0.09%)H范围内，均未超过深层水平位移报警值50 mm(0.27%H)，且最大位移数值距报警值尚有33.4 mm，约0.18%H。

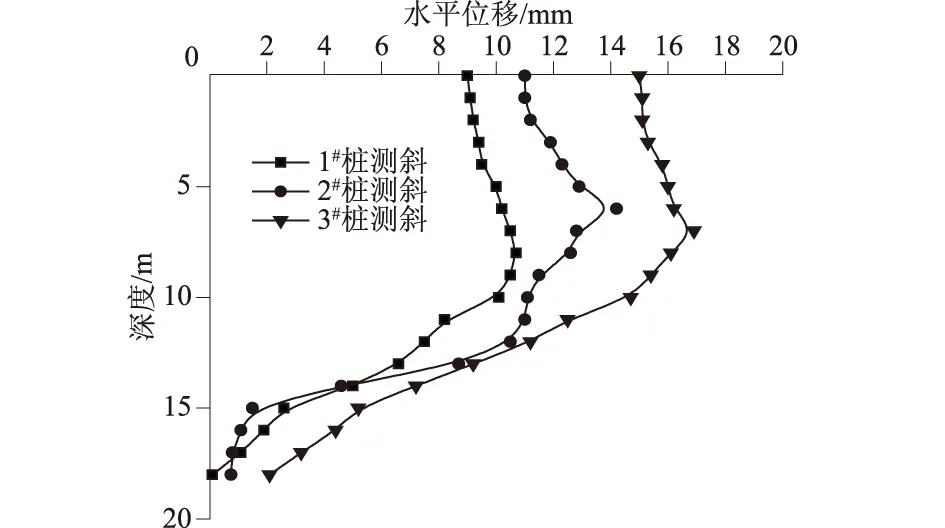
图10　围护桩深层水平位移Fig.10　Deep horizontal displacement of supporting pile

图10中显示围护桩的最大位移值出现在支护桩的第3道锚索附近，距离坑底8 m左右。且各支护桩的位移形状基本相同，出现“鼓肚”现象。桩底部的位移很小，未出现“踢脚”现象，在浇筑底板期间上半部分土体未发生明显的蠕变，反而出现了回移现象。基坑已开挖到设计标高，土体荷载充分释放，基坑下半部分土体产生了蠕变变形[16]。

5.2　桩顶竖向位移

图11所示，1#桩的竖向变形较大，竖向位移最大值为8.9 mm(约0.05%H)，未超过桩顶最大竖向位移报警值0.08%H，最大竖向位移距报警值约为0.03%H。

图11　桩顶竖向位移Fig．11　Verticaldisplacementatthetopofsupportingpile

6　结　论

(1)考虑土压力折减系数，基于黄河厚冲积平原深基坑插入比统计分析，得到了不同地面均布荷载所对应的最优插入比参考取值。

(2)根据数值模拟的结果，当插入比<0.4时，基坑变形较大，继续增大插入比，可显著提高基坑稳定性；当插入比>0.55时，继续增加插入比对减小基坑变形作用并不明显，造价却大大提高。因此，根据本文的研究结果综合判断插入比的合理设计值为0.55。

(3)通过对实测数据进行分析可得：插入比在0.58时，围护桩侧向位移、沉降的变化幅度不大，距离报警值有一定的安全储备，此时桩端持力层为第⑥层黏土，上层为粉质黏土，两者均属“黏性土”，工程力学特征相近，因此理论计算和数值模拟结果符合工程规律和实践要求，可以实现支护优化。

参考文献：

[1]POH T Y, WONG I H, CHANDRASEKARAN B. Performance of Two Propped Diaphragm Walls in Stiff Residual Soils[J]. Journal of Performance of Constructed Facilities, 1997, 11(4): 190-199.

[2]高新南, 刘松玉, 童立元. 苏州地铁车站基坑多支点咬合桩插入比分析[J]. 东南大学学报, 2012, 42(3) : 352-357.

[3]李淑, 张项立, 房倩, 等. 北京地铁车站深基坑地表变形特性研究[J]. 岩石力学与工程学报, 2012, 31(1): 189-198.

[4]杨将, 彭加强, 周奇辉, 等. 基于单因素分析的某深基坑优化设计[J]. 铁道工程学报, 2009, 126(3): 84-88.

[5]陈斌, 施斌, 林梅, 等. 南京地铁软土地层咬合桩围护结构的技术研究[J]. 岩土工程学报, 2005,27(3): 354-357.

[6]武朝军, 陈锦剑, 叶冠林, 等. 苏州地铁车站深基坑变形特性分析[J]. 岩土工程学报, 2010, 32(7): 458-462.

[7]李四维, 高华东, 杨铁灯. 深基坑开挖现场监测与数值模拟分析[J]. 岩土工程学报, 2011, 33(8): 284-291.

[8]徐飞, 王渭明, 张乾青, 等. 黄河冲积平原地区超大型深基坑开挖现场监测分析[J]. 岩土工程学报, 2014, 36(11): 471-478.

[9]杨校辉, 朱彦鹏, 郭楠，等. 地铁车站深基坑桩锚支护结构内力试验研究[J]. 岩土力学, 2014, 35(10):185-197.

[10] 陈力华, 靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报, 2012, 45(9):136-146.

[11] 陈国庆, 黄润秋, 周辉,等. 边坡渐进破坏的动态强度折减法研究[J].岩土力学, 2013, 34(4): 1140-1146.

[12] GB 50009—2012,建筑结构荷载规范[S]. 北京：中国建筑工业出版社,2012.

[13] 陆培毅, 刘畅.弹性抗力法确定支护结构插入深度的研究[J]. 岩土力学, 2002, 23(6):750-753.