土石混合料填方体原位剪切试验方法探讨

2018-04-17，，，，

长江科学院院报 2018年4期

　，，，，

(1.贵州桥梁建设集团有限责任公司总工程师办公室，贵阳　550004；2.中国电力工程顾问集团中南电力设计院有限公司勘测工程公司，武汉　430071)

1　研究背景

近年来，随着我国工程用地的日渐紧张，外加考虑到工程施工对人居环境的负面影响,许多诸如电厂、变电站等大型国家重点工程项目已“迁移”到山区。而山区地质条件复杂，在场区回填过程中为了尽可能保证挖填方平衡，采用的填料成分大多为残坡积的土石混合料，同时由于山区地形起伏较大，往往形成大范围的混合料填方边坡。这种人工边坡的滑动以及挡土结构物的移动和倾倒等都主要是由于作用于土石混合料内部的剪切应力超过自身的抗剪强度而引起的。工程设计人员必须基于土石混合料的抗剪强度参数进行边坡稳定性计算和支护设计，而现场原位剪切试验可最具针对性地获取土石混合料抗剪强度参数,直接在工程现场选取一定数量的典型场地，就地进行试验，可避免试样获取、搬运过程中土样搅动的影响。

但由于土石混合料内部含有粒径较大、强度较高的块石，而且影响其物理力学性质的因素也较多，受到技术及测试手段的限制，从受力方式的角度对土石混合料的原位剪切试验只有水平推剪和原位直剪2种类型。在此，借鉴前人的试验成果，指出这2类原位剪切试验存在的问题，并基于试验结果对比分析。对比分析结果可为土石混合料的进一步试验研究提供参考。

2　现场原位剪切试验

直接剪切仪(直剪仪) 是岩土工程中最早使用的一种测定土样抗剪强度的仪器。它具有操作直观简单方便的特点, 并且在岩土力学教学和实际工程测试中被广泛使用。

目前为止，研究成果中原位大型直剪试验大部分采用的是单剪切盒的形式，而剪切盒的形状有圆形和方形2种，尺寸相差较大，具体统计见表1。加载示意图如图1所示。

表1前人研究的土石混合料原位直剪试验方案统计
Table1Somearrangementsofinsitudirectsheartestonsoil-rockmixtureinpreviousstudies

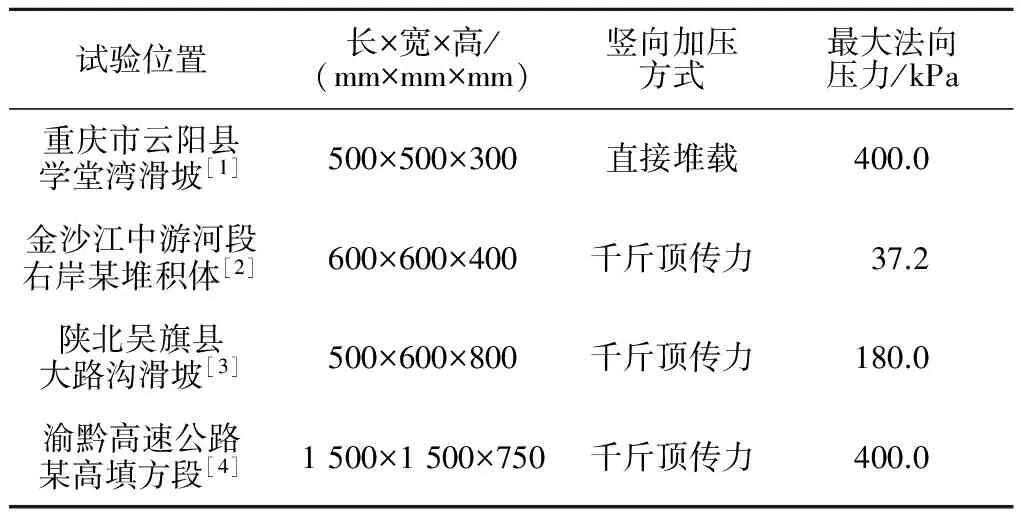
试验位置长×宽×高/(mm×mm×mm)竖向加压方式最大法向压力/kPa重庆市云阳县学堂湾滑坡[1]500×500×300直接堆载400．0金沙江中游河段右岸某堆积体[2]600×600×400千斤顶传力37．2陕北吴旗县大路沟滑坡[3]500×600×800千斤顶传力180．0渝黔高速公路某高填方段[4]1500×1500×750千斤顶传力400．0

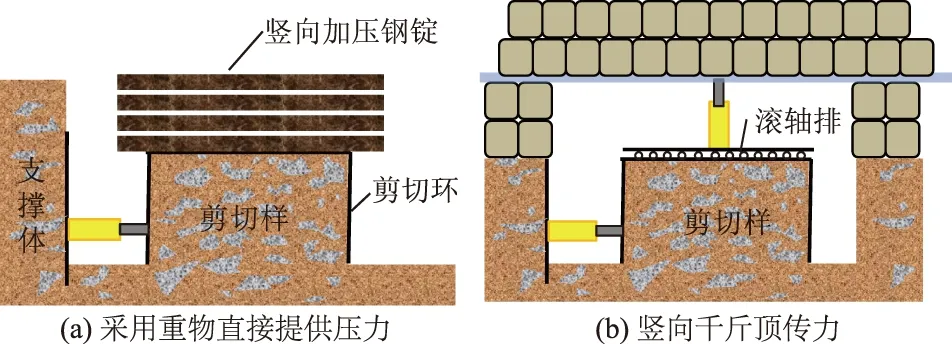
图1　原位大型直剪示意图Fig.1　Schematic diagram of large-scale in-situdirect shear

原位直剪试验因理论基础简单明了，使用操作方便，在工程上具有广泛的应用性。但结合前人研究成果发现原位直剪试验具有一些不足之处:

(1)法向反力施加不便，在法向压力选择时，为了保证强度参数的适用性，必须保证法向压力大于最大上覆土层自重和附加应力之和。若采用如图1所示的加载形式，难以采用法向钢锭提供足够的法向反力。在法向加压的过程中极易失稳或者出现钢锭板直接压在剪切盒侧壁上面造成试验结果失真。而且在剪切过程中整个法向加压系统沿着剪切方向平移，易发生法向加压钢锭侧翻而导致试验失败。

(2)水平荷载失真。为了避免在剪切过程中法向加压系统沿剪切方向的平移问题，学者们提出在土样顶部和法向加压千斤顶之间增加滚轴(珠)排系统，但是在法向压力作用下，滚轴排系统滚动所需克服的摩阻力往往使试验结果偏于冒进。

(3)剪切盒尺寸问题。表1所列为国内各学者们开展的土石混合料原位直剪试验采用的剪切盒尺寸，基本为方形，尺寸从500 mm到1 500 mm不等。在研究成果中未说明剪切盒尺寸确定的依据和原则，也未交待适用的剪切样最大颗粒粒径等因素。与室内试验可根据设备调整粒径不同，原位试验必须根据工程现场最大颗粒粒径和含石量综合考虑剪切盒的尺寸。为了防止剪切面上靠近剪力盒的颗粒自身剪碎造成抗剪强度偏大假象的发生，力求剪切盒尺寸足够大。但是过分加大仪器尺寸，一方面会大大增加试验的难度和工作量, 另一方面剪切过程中背离剪切方向一侧土石混合料受挤压严重，明显影响试验结果。

(4)剪切缝预留不当造成试验结果失真。当土石混合料中粗集料为硬质岩时，剪切面直接剪破岩块的可能性不大，剪切面附近长轴方位与所在位置剪切面方位不一致的岩石碎块发生翻滚、移位，并扰动周边土体，使剪切面由面发展成为一个剪切带，这个带状体厚度要求剪切前应预留一定的剪切缝宽度。而在原位剪切之前，要准确地估计剪切带厚度很难，其原因为：如果缝隙尺寸太小,盒壁将制约颗粒的滚动和错动，造成抗剪强度偏高；如果缝隙尺寸太大，剪切过程中试料会挤出，从而有效剪切面积减小，剪切面上土的密度变小，抗剪强度偏低，试验结果也不能反映土石混合料的真实剪切特性。翁厚洋等[5]提出剪切缝宽度可取为颗粒最大粒径或平均粒径的某一倍数，但是土石混合料剪切带的厚度除了与土石混合料的粒度组成有关以外，还与土石混合料的含石量有很大的关系，如图2所示[2]。徐文杰等[2]原位直剪结果发现随着块石含量的增加，其剪切带逐渐变宽。

图2　不同含石量土石混合料剪切带发育Fig.2　Development of shear zones in rock-soilmixture with different rock content

除此之外，原位大型直剪试验的结果分析还存在以下不足：

(1)在剪切应力计算时，假定剪切面为平面。而在土石混合料内部存在大量的超径颗粒，剪切过程中剪切面常常发生“绕石”现象，剪切面为一曲面。

(2) 试验结果离散性较大，由于土石混合料的极度不均匀性，即使是相邻位置的试件，回归相关系数较低，由不同位置的试件进行强度指标比较时，甚至出现负相关。

3　原位水平推剪试验

由于考虑到原位直剪试验至少需要3～4个试样才能得到一组强度参数值，但是土石混合料各试样间的粒度组成之间相差较大，造成强度参数失真。学者们采用了水平推剪试验测取土石混合料的强度参数，并取得了一些有意义的研究成果，统计见表2。

表2　前人研究的土石混合料原位水平推剪试验方案Table 2　Some arrangements of in situ push-shear test onsoil-rock mixture in previous studies

水平推剪试验是在现场选取具有代表性的试验点，开挖成三面临空的半岛形试验体，其试验示意图见图3，两侧挖出后与周围土体脱开后，加上限制板后回填土体，受力状态类似于平面应变状态。在前部采用刚度较大的传力板加压，剪切破坏面为一曲面，这一曲面上竖向荷载为土体自重，水平荷载为试验时的加载。通过试验完成后的破坏面测定、土体自重测定、水平加压时的最大荷载值Pmax和剪断后纯摩擦荷载值Pmin按条分法的极限平衡理论计算得出强度参数值。

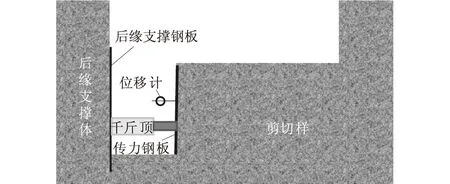
图3　水平推剪法试验装置简图Fig.3　Schematic diagram of in-situpull-shear test apparatus

水平推剪试验虽然在试验操作上面要比原位直剪试验方便快捷，但是在前提假设等方面存在以下问题，制约了其在工程上的应用性。

(1)水平推剪试验因为试样表面并无附加法向应力，所以其力学参数只能用于浅层滑坡稳定性分析。而对于深层滑面，无法向应力的水平推剪试验无法模拟深层滑面的受力状态。

(2)试样尺寸问题，即土石混合体具有典型的尺寸效应。李晓等[8]进行不同尺寸的原位水平推剪试验发现，在试样尺寸较小的情况下，破裂面的发展显得较为凌乱，破裂面的发展受块石的影响比较大，而在试样尺寸加大的情况下，破裂面的发展虽然仍受到块石的影响，相对平滑、规则，而反映在水平推力-剪切位移曲线上的特征则是，在含石量基本相同的情况下，最大荷载值Pmax明显下降。

(3)剪切滑动面的确定问题。由于假定试样在剪切过程中处于平面应变状态，《工程地质手册》(第4版)中给出的强度计算公式均为平面应变状态下的强度参数，均是基于在宽度方向上各处剪切面一致的假定提出，表2所列试验在成果分析时均是基于这种方式得出强度参数值。笔者在云南某大型土石混合料高填方体表面进行了大量的土石混合料原位水平推剪试验发现，由于土石混合料中粒度组成复杂，各粒组颗粒空间分布极不均匀造成剪切破坏面在宽度方向极度不均匀(见图4)。选取某一测面作为强度计算剖面均会引起不可忽视的误差，即使采用徐文杰等[7]提出的“平均剪切面”可在一定程度上减少因计算滑面选取的随机性带来的误差，但是对于如图4所示两侧滑面长度明显不等的情况采用“平均剪切面”不能得出准确的强度参数值，有必要将水平推剪试验的三维极限平衡理论完善[11]，以扩大水平推剪试验的工程适用性。

图4　现场大型推剪试验土石混合料剪切面Fig.4　Shear face of large-scale in-situ pull-sheartest on soil-rock mixtures

(4)传力钢板定向移动问题。原位水平推剪试验设备简单，操作方便。但是在推剪过程后期，由于变形过大，外加土石混合料内部组成的不均匀性，容易出现两侧受力不均发生传力钢板发生偏斜，影响试验结果。

(5)剪切体中部断裂问题。在剪切进程后期，最理想情况是剪切整体剪出，如图5(a)所示，剪切体底部自始至终处于受剪状态。但是在原位水平推剪试验过程中，剪切面并非标准的下凹面，剪切面出现轻微上凸趋势时，剪切体在剪切上抬过程中容易发生中间断裂，两部分剪切体发生中部隆起，底部脱空现象(如图5(b))，而此时水平推力已超过峰值Pmax，脱空现象仅造成剪断后纯摩擦荷载值Pmin偏高的假象。

图5　剪切体中部断裂Fig.5　Fracture of shear body

4　原位直剪和水平推剪试验对比

从前面阐述中可发现，原位大型直剪和水平推剪对土石混合料力学特性的揭示各有侧重，在前提假设和试验操作过程中也都存在一些不足。由于理论基础不尽相同，有必要对同一种土石混合料采用不同原位剪切试验，对二者的差异性进行对比分析。

李晓等[8]曾采用80 cm×80 cm×25 cm方形剪切盒对含石量为35%～50%的重庆奉节县白衣庵土石混合体滑带土进行原位直剪和水平推剪的对比性试验研究，对两者试验结果中的应力-应变特性、剪切破坏形式和特征进行了总结。认为推剪试验能反映土石混合料的全应力-应变曲线特性，并表现出明显的应力屈服和塑性变形特征。在推剪作用下土石混合料的破裂面形态为典型的滑弧面，尽管不同试样的破裂面形态有所差异，但其在力学机制上基本体现为推剪作用下典型的剪切破坏面。而原位直剪则不同，虽然在一定程度上固定的剪切破坏的范围，但是由于土石混合料内块石成分在结构上形成的结构差异性，在法向压力作用下试样后部应力差比较大，土石混合料的破坏特征呈现压裂面与剪切面共存的典型现象。但是遗憾的是李晓未对这2种原位剪切试验的强度参数进行对比分析。

为此，笔者在云南某大型土石混合料高填方体相同的地点分别进行了3组原位直剪和水平推剪的对比性研究。

原位直剪采用的是直径60 cm，高20 cm的圆形剪切环刀，原位水平推剪的试样尺寸长×宽×高为108 cm×66 cm×30 cm。剪切宽度选66 cm,比现场大型直剪环的直径大10 cm,以便推剪时安装方便。土石混合料由于粗集料的存在无法精确修整出标准矩形，所以一边预留出5 cm采用原土回填修平。

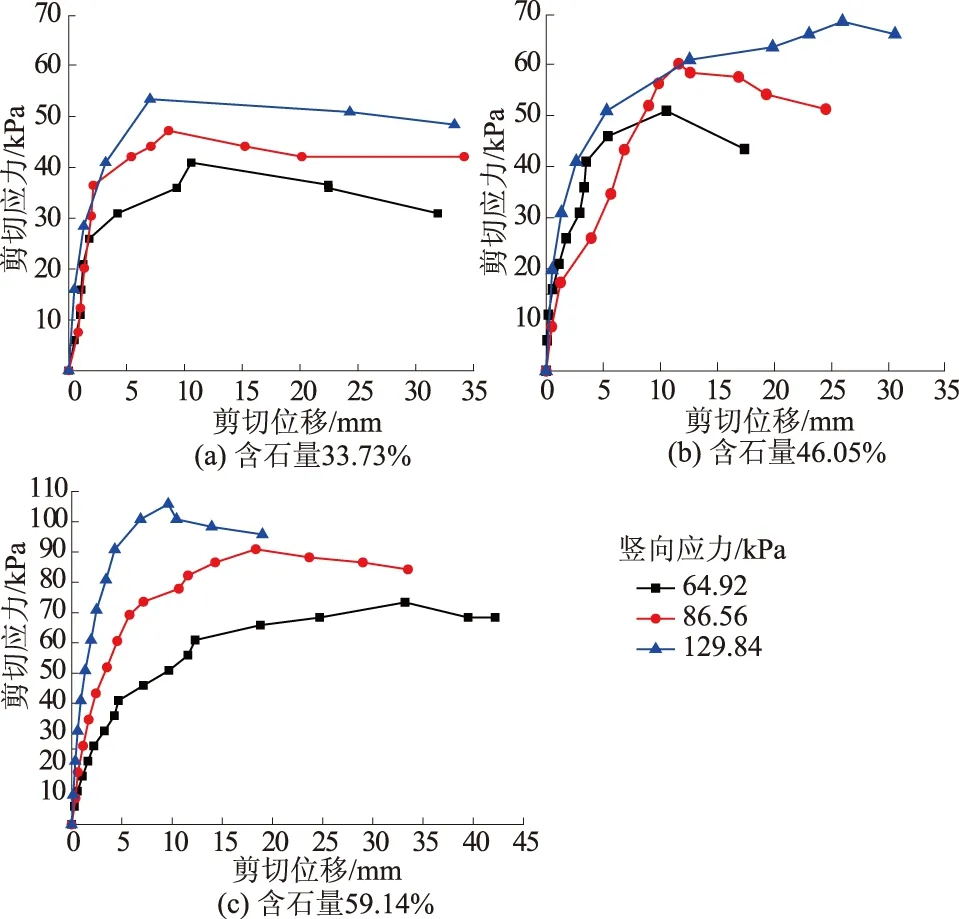
图6　3组原位直剪试验剪应力-位移曲线Fig.6　Curves of shear stress vs. displacement forthree groups of direct shear tests

3组原位直剪试验的应力-应变曲线见图6，当剪切位移进展到约10 mm时，大部分曲线的剪切应力达到峰值，所以直剪试验剪应力-剪切位移曲线大致可分为2个阶段：①双曲线段(0～10 mm)；②软化阶段，当剪切位移约>10 mm后，剪切即呈现软化规律，剪应力出现小幅骤降。

由于剪切盒在一定程度上限制了剪切面，所以剪切破坏大体上沿着剪切盒底部剪出。但是由原位直剪试验现象(图7)可见，剪切面不是标准平面，剪切面附近块石长轴方向与剪切面锐角相交的，基本发生如图4所示的“绕石”效应。当块石长轴方向与剪切面呈钝角相交时，在剪切过程中，块石势必发生翻滚移位。直剪试验的盒缘对块石侧向有明显限位作用(见图7(a))，此时会造成剪切应力“虚高”。进一步的剪切会直接剪碎块石(见图7(b))，块石剪碎后，剪切即迅速进行软化阶段。剪切盒对试样的侧限还进一步改变了土石混合料的平面剪切假定，相对剪切试样而言，剪切盒下方岩块所受侧限作用有限，本次大型直剪试验发现剪切带向理想剪切的下方发展，呈“下凹”形(见图7(c))。这一现象在图2中也有体现[2]。

图7　原位直剪试验现象Fig.7　Build-in of rocks, shear crush, and concaveshear face during in-situ direct shear test

为了进行试验对比，在原位直剪试验点旁边选取试验点进行原位水平推剪试验。3个水平推剪的水平推力-水平位移曲线见图8。试验时为了消除由于传力板偏转对试验结果的影响，在传力千斤顶两侧10 cm对称布置2个剪切位移测试点。2个测试点到位移的距离分别记为剪切位移1和剪切位移2，将剪切位移1和剪切位移2平均可得传力板的平均剪切位移。结合现场观察到的剪切体表面现象，分析剪切进展的详细过程。推剪前期水平推力随剪切位移基本呈线性增长(剪切位移在0～5 mm范围)。当水平荷载增大到一定值时剪切样表面出现放射形裂纹，随着水平荷载的加大，原有裂纹缓慢增宽增长并伴随出现了次生裂纹。当水平荷载加载到峰值后，后期荷载不增反降，剪切进行到软化阶段。与原位直剪试验相比，原位水平推剪试验并未严格限制剪切方向，所以剪切破坏面相对更加平滑、规则(见图9)。原位大型直剪试验和水平推剪试验得出的强度参数值对比见表3。

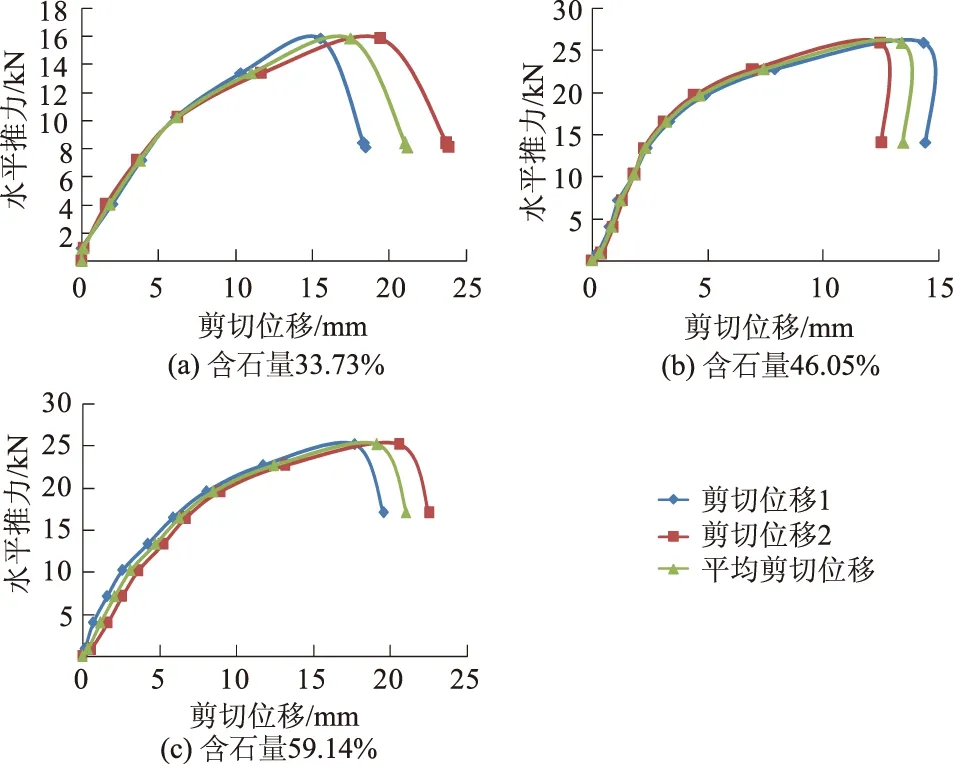
图8　水平推剪试验水平推力-剪切位移曲线Fig.8　Curves of horizontal push force vs. displacementfor three groups of push-shear tests

图9　水平推剪试验的剪切破坏面Fig.9　Shear faces in three groups of pull-shear tests

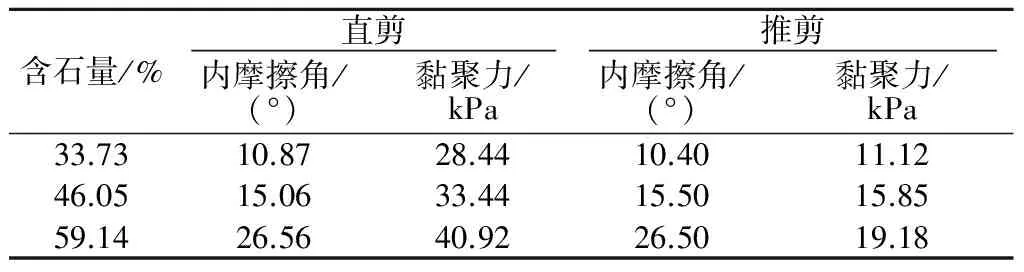
含石量/%直剪推剪内摩擦角/(°)黏聚力/kPa内摩擦角/(°)黏聚力/kPa33．7310．8728．4410．4011．1246．0515．0633．4415．5015．8559．1426．5640．9226．5019．18

从表3中可见，2种试验方法得出的内摩阻角差别不大，但是黏聚力相差太大。其原因一方面是直剪试验剪切盒对试样中岩块的限制现象使得岩块间相互嵌固，呈现出假黏聚力。另一方面是剪切滑动面下凹现象都使得试验结果计算时的理论剪切面积比实际剪切受力面积要小。两方面原因综合导致了原位直剪试验得到的黏聚力偏高。

而水平推剪试验的黏聚力计算公式为

(1)

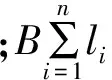
Pmax的取值无争议，而Pmin的取值有3条标准：

(1)千斤顶加压到Pmax后，即停止加压，使油压表读数后退并达到稳定值。

(2)观测试样刚开始出现裂隙时的压力表读数。

(3)当千斤顶加压到Pmax后，松开油阀，然后关上油阀重新加压后所能确定的峰值。

第(2)条取值原则机理不清晰，而且由于在加载过程中分级加荷，表面裂隙有可能开展于2级荷载之间，而剪切变形滞后于千斤顶加压，造成压力表读数高于实际的Pmin值。笔者在通过现场试验发现第(2)条取值原则有很强的随机性，与第(1)条和第(3)条所得的荷载值相差较大；而第(1)条和第(3)条取值的假定是在剪切面贯通后，剪切体和下部岩土体已完全脱开，此时剪切破坏面黏聚力已发挥完毕，后期的荷载或反复加荷时荷载主要由摩擦力承担。笔者在试验中发现第(1)条和第(3)条取值原则在数值上具有高度一致性，建议后期的推剪试验应根据这2条取值原则获取Pmin值。