基于多种优化支持向量机及V/S分析法的隧道变形预测及趋势判断

2018-04-17

长江科学院院报 2018年4期

(陕西铁路工程职业技术学院，陕西渭南　714000)

1　研究背景

在我国交通建设过程中，隧道施工具有避免形成高路堑、缩短建设里程等优点，且在隧道施工过程中，隧道开挖会引起围岩变形，若不加以控制，有导致塌方的危险。因此，在隧道施工过程中，会对隧道的变形进行监测，以掌握隧道变形量，指导现场施工。同时，通过已有监测信息，挖掘出隧道的变形规律，对后期变形进行预测，能更好地实现监测目的。

由于岩体的复杂性，使得隧道的变形具有很强的非线性特征，预测过程具有较大的困难，不过仍有较多学者在这方面进行了研究，其中支持向量机是最为常用的预测方法之一，如赵洪波[1]利用支持向量机对隧道变形进行非线性预测，验证了该方法具有简单适用的特点，可行性较高。但传统的支持向量机模型，其参数很大程度上依赖使用者的经验，所以许多学者将多种优化算法引入到支持向量机的参数优化过程中，如刘开云等[2]、刘宇[3]、罗亦泳等[4]采用遗传算法对支持向量机进行优化，并通过实例检验了该方法能很好地提高预测精度，具有较高的预测能力；李晓龙等[5]利用最小二乘法对支持向量机的核函数进行优化，提高了核函数的推广能力，并经实例验证该模型的有效性；范思遐等[6]利用粒子群算法增加了支持向量机的收敛速度和搜索能力，实例验证了该模型具有较高的鲁棒性及计算精度。

上述研究都很好地说明支持向量机在隧道变形预测中具有较高的预测能力，但不同模型预测所需的信息及适用性具有较大的差异，因此，本文将上述优化模型应用到本文实例中，以探讨不同预测模型的适用性和有效性。该理论也被广泛的研究，如邬长福等[7]将该理论应用到滑坡变形趋势的判断中，且实例效果较好；左昌群等[8]则利用该理论对隧道地表沉降进行了预测分析，得出预测值与实测值之间较为接近，较传统分析方法有了较大的提高，验证了该理论的有效性。因此,本文采用分形理论的V/S分析法对隧道变形趋势进行判断，以掌握隧道变形的发展趋势。另外，由于监测过程中，会包含较多的误差因素，对变形预测结果有较大的影响，所以采取卡尔曼滤波对隧道的监测数据进行滤波处理。

综合上述，本文采用多种优化支持向量机及V/S分析法对隧道变形进行预测及趋势判断，为隧道的变形预测提供一种新的思路。

2　基本原理

2.1　研究思路

本文充分利用多种优化支持向量机模型对隧道的变形进行预测，并利用V/S分析法对隧道的变形趋势进行判断，进而实现隧道变形趋势的综合判断研究，思路如下：

(1) 利用3次样条插值对隧道变形的原始监测数据进行预处理，实现隧道变形由非等距时间序列转变为连续时间序列，为后期变形预测及趋势判断奠定数据基础。

(2) 利用多种卡尔曼滤波对隧道变形数据进行滤波处理，分解出隧道变形数据含有的误差信息，实现隧道变形趋势项及误差项的分离。

(3) 采用粒子群法、最小二乘法及遗传算法优化支持向量机，并对隧道变形的趋势项序列进行预测；同时，进一步利用变异系数法探讨不同优化方法的效果，确定出各优化模型的组合权值，综合确定出趋势项的预测值。

(4) 利用BP神经网络对隧道变形的误差项序列进行预测，并采用试算法研究不同隐层节点模型在隧道趋势项预测中的效果；并将趋势项和误差项的预测结果综合得到隧道的变形预测值。

(5) 采用分形理论的V/S分析法，对隧道的变形序列和速率序列进行发展趋势判断，并与预测结果进行对比，以验证前文预测模型的有效性。

2.2　卡尔曼滤波

本文采用了MatLab的拟合工具箱实现隧道变形数据的3次样条插值，通过3次样条插值能实现变形数据的等距划分，利于后期数据的处理。同时采用卡尔曼滤波对隧道的变形数据进行去噪处理，但由于传统滤波过程中，会出现递推扩散、抵抗力弱等缺点，因此特地引入了相应的参数分量，对滤波过程进行优化处理，达到有效滤波的目的。

在文献[9]中提出多种滤波模型，得出不同滤波模型之间具有较大的差异，因此本文也探讨标准、自适应、抗差自适应及半参数卡尔曼滤波在隧道监测数据滤波中的适用性，且由于相关文献[9]已对各滤波模型的基本原理进行了详述，此处则不赘述其基本原理。同时，采取信噪比及均方根误差作为基础指标，以两者的归一化处理值之和作为综合评价指标，对各模型的滤波效果进行评价。

2.3　支持向量机

支持向量机(SVM)能实现输入信息映射到高维空间的非线性变换，其基于最小化的结构风险原则，求解在有约束条件下的二次规划问题，进而得到全局最优解，泛化能力及推广能力均较强，能很好地解决非线性、局部极小点等问题。

隧道变形具有非线性特征，其变形序列可表示为x={x1,x2,…,xn}，结合支持向量机的基本理论，得出变形值xi+p与前p个变形值之间存在着非线性关系，即

(1)

式中：f(xn+m)为在n+m时刻的变形值；Xn+m为n+m时刻前p个时刻的变形值；Xi为p+i时刻前p个时刻的变形值；f(·) 为核函数；a,a*,b为二次规划求解参数。

在求解二次规划参数的过程中，其求解公式为：

(2)

(3)

但是，在支持向量机的应用过程中，较多的模型参数仍是依据使用者的经验进行设定，降低了使用效率，也减弱了支持向量机的逼近能力等。为取得较好的预测结果，许多学者将多种优化算法引入到了支持向量机的参数优化中，但不同的优化算法具有其适用性，因此本文探讨粒子群算法、最小二乘法和遗传算法对支持向量机优化后在实例中的适用性。

2.3.1粒子群算法

粒子群算法是将优化对象看作粒子，粒子最终的最优位置则被视为全局最优解，并在优化过程中，权重系数w对最终的优化结果具有重要的影响，且为提高权重系数的搜索性能，将其搜索过程分解为2个过程:在第1个搜索过程中，权重系数以加速递减的方式确定最优解的阈值范围；在第2个搜索过程中，权重系数以减速递减的方式逐步收敛到最优解。同时，在权重系数搜索的定义域中，增加平方控制调节，以增加权重系数的非线性能力，使其不易陷入局部最优值，其表达方式为

(4)

式中：wmax,wmin分别为权重系数的最大值和最小值；k为平滑度控制因子；tmax为种群最大迭代数；t为种群的当代迭代数。

2.3.2最小二乘法

最小二乘法对支持向量机的优化主要是体现在将传统支持向量机的不等式约束转变为了等式约束，约束形式为

yi=wTφ(xi)+b+ei,i=1,2,…,l。

(5)

式中：w为权重系数；b为偏执因子；ei为矩阵函数。

同时，最小二乘法优化支持向量机还能将经验风险项由一次转化为了二次，实现结构风险的调整。

2.3.3遗传算法

预测的目的是期望预测误差值最小，且遗传算法通过适应函数对支持向量机预测进行非线性加速，其表达式为

g(x)=exp(-0.001s2)。

(6)

式中：g(x)为适应函数；s2为预测误差平方和均值。

为实现预测误差值为0，适应函数就应为1，且适应函数的最大值即为1。因此，通过遗传算法对支持向量机的改进，能使适应函数不断地接近1，进而实现训练精度的提高。

另外，采用变异系数法对多种优化模型的预测结果进行评价，且以变异系数值为指标，确定各模型的组合权值，实现趋势项优化后的组合预测，提高预测精度。

2.4　V/S分析法

V/S分析法是由Cajueiro等在R/S分析法的基础上改进得到的，其改进主要是利用方差替代累计离差的极差，统计量的表示主要为

(7)

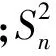
V/S统计量与其对应子序列长度n之间存在对应关系，即能得到(n,(V/S)n)的散点图，且lg(V/S)n和lgn之间存在线性关系，即

lg(V/S)n=lgC+2Hlgn。

(8)

式中：C为常数；H为Hurst指数。

3　实例分析

3.1　实例概况

图1　 3次样条插值后拱顶下沉-时间曲线Fig.1　Curve of vault subsidence against timeafter three spline interpolations

以文献[2]中的富溪隧道为例，数据来源于该隧道左线ZK205+932断面的拱顶变形监测数据。由于监测过程是按非等距监测，因此本文首先采取MatLab中的cftool工具箱对监测数据进行3次样条插值，将监测数据转变为等距序列，转变后的变形监测数据如图1所示。通过隧道拱顶的累计变形曲线，得出隧道拱顶在前9个周期的变形增量较大，而在监测后期的变形相对平缓。

3.2　卡尔曼滤波处理

采用标准、自适应、抗差自适应及半参数4种卡尔曼滤波对隧道的拱顶变形监测数据进行滤波处理，结果如表1所示。

表1　卡尔曼滤波处理结果统计Table 1　Statistics of Kalman filtering results

由表1可知，通过对滤波过程进行参数优化后的滤波结果均优于标准卡尔曼滤波的滤波结果，说明对滤波过程中的参数优化具有其必要性；同时，对比4种滤波模型的效果，得出以半参数卡尔曼滤波的效果最优，因此本文以半参数卡尔曼滤波的结果作为趋势项及误差项分离的依据；另外，各基础指标及综合指标之间的评价结果均具有较好的一致性，说明本文滤波结果的可信度高。

3.3　趋势项预测

采用多种优化的支持向量机对隧道变形的趋势项进行预测，得到的预测结果如表2所示。

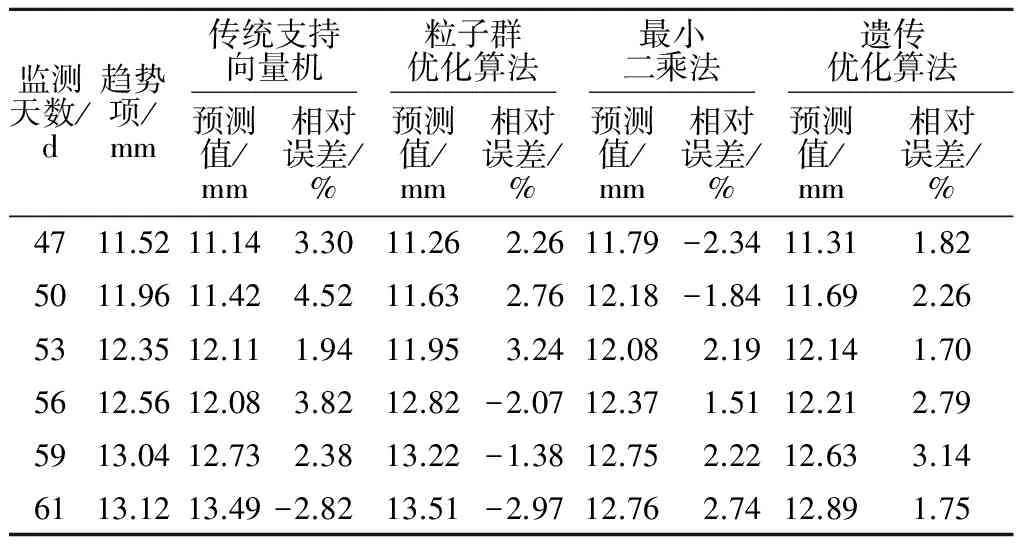
表2　趋势项预测结果统计Table 2　Statistics of trend term forecast results

通过表2对比不同优化模型的结果，得出不同优化模型的预测结果具有一定的差异，说明不同优化模型具有其适用性；同时，对比优化支持向量机与传统支持向量机之间的预测结果，得出通过参数优化，有效提高了预测精度，验证本文预测思路的有效性。为进一步分析各预测模型之间差异特征，再对各模型预测结果的变异系数进行统计，结果如图2所示。

图2　不同模型的变异系数对比Fig.2　Comparison of coefficient of variationamong different models

由图2可知，3种优化模型的变异系数均小于传统预测模型的变异系数，说明传统预测模型的预测结果较优化模型的预测结果具有更高的波动性和离散性;且在4种预测模型中，最小二乘法优化的支持向量机预测模型具有最优的预测结果。

同时，以变异系数为权值评价指标确定出3种优化模型的权重系数为[0.290 70.408 40.300 9]，依据权重系数得出隧道变形趋势项的组合预测结果如表3所示。

表3　趋势项组合预测结果Table 3　Combinatorial prediction results of trend term

由表3可知，通过对优化模型的组合预测，提高了预测精度，得出趋势项预测的最大相对误差值为2.35%，其余相对误差大部分<1%，说明本文组合预测思路具有可行性。

3.4　误差项预测

采用BP神经网络对隧道变形的误差项进行预测;且考虑到网络隐层节点数对预测结果具有较大的影响，采用试算法确定最优隐层节点数，不同隐层节点数的试算结果如表4所示。

表4　隐层节点试算结果Table 4　Trial calculation results of hidden layer nodes

通过对不同节点数的试算，得出隐层节点对预测结果具有较大的影响，其中，隐层节点数为12时的预测效果最优，其累计误差值为0.218 mm，累计相对误差值为16.43%。因此，本文将隐层节点数设置为12，误差项相应的预测结果如表5所示。

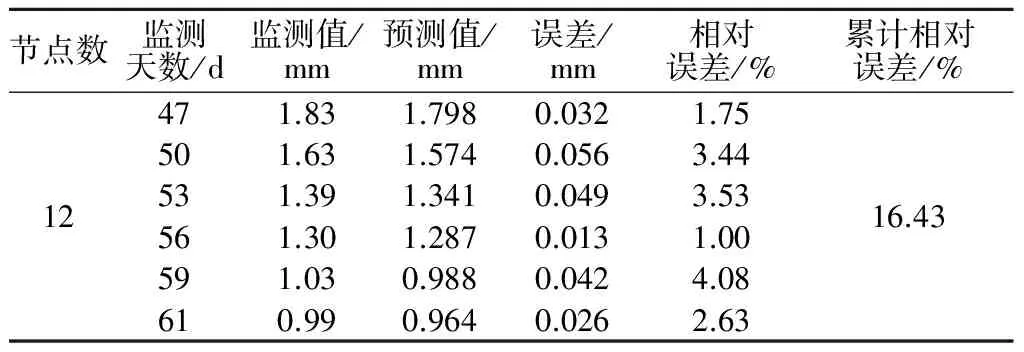
表5　误差项预测结果统计Table 5　Statistics of error prediction results

通过对误差项的预测，得出其最大相对误差为4.08%，最小相对误差为1%。对比趋势项的预测结果可知，误差项的相对误差要大于趋势项的相对误差，这与误差项含有较多的随机信息有关，也说明了前文采用卡尔曼滤波分离趋势项和误差项的有效性。

基于前文对趋势项和误差项的预测，综合得到隧道的变形预测值，并对隧道变形的后4个周期进行预测，以判断隧道未来的变形趋势，结果如表6所示。对比文献[2]的预测结果，本文的预测精度有了较大的提高，也验证了本文预测模型的有效性。

表6　隧道拱顶变形预测Table 6　Prediction of tunnel vault deformation

由表6可知，隧道在未来4个周期的变形预测值仍在增加，说明隧道变形为增长趋势。

3.5　隧道变形V/S分析

为进一步分析判断隧道的变形趋势，本文再利用V/S分析法对隧道的变形进行趋势判断。同时，为达到全面分析的目的，对隧道变形的变形序列和速率序列均进行了分析，相关统计量如表7所示。

表7　隧道V/S分析统计Table 7　Statistics of V/S analysis result

由表7可知，两序列的Hurst指数均>0.5，说明隧道的变形具有正向持续增长的趋势，且变形序列的Hurst指数要大于速率序列的Hurst指数，说明通过变形序列判断隧道的趋势性更加明显，反之速率序列相对更为保守。同时，变形序列的分形维数要大于速率序列的分形维数，且两序列的相关性指标CM统计量均为正，说明两序列均呈正相关，且变形序列的相关性要明显大于速率序列的相关性。另外，两序列的拟合度均较高，且误差平方和SSE统计量(残差平方和)均较小，说明在线性拟合过程中，拟合效果较好，求得的Hurst指数具有较高的可信度。

考虑到隧道变形序列具有一定的相关性，因此本文采用AR(1)模型对两序列进行处理，旨在剔除两序列的相关性，并对处理后的序列再进行V/S分析，结果如表8所示。

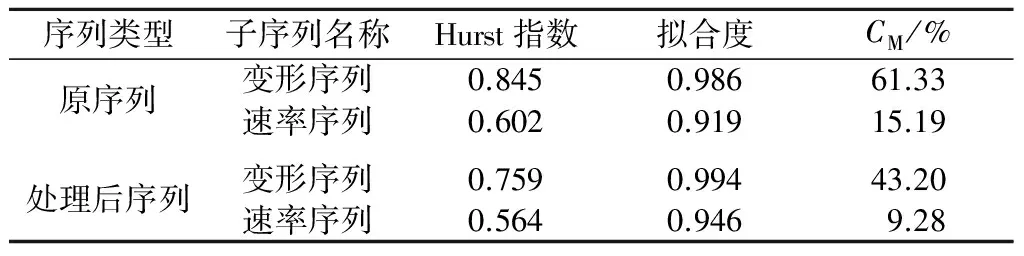
表8　 AR(1)处理后的V/S分析统计Table 8　Statistics of V/S analysis result afterAR(1) processing

由表8可知，经过对序列相关性的剔除，两序列的Hurst指数均出现不同程度的减小，但两序列的Hurst指数仍>0.5，说明两序列仍具有正向持续增长的趋势，验证了V/S分析结果的准确性。同时，两序列在处理后的拟合度也得到了不同程度的提高，说明通过AR(1)模型处理两序列的必要性。另外，处理后序列的CM统计量均出现了不同程度的减小，说明通过AR(1)模型处理能有效减小序列的相关性，验证了本文思路的有效性。

对比前文的预测及V/S分析的结果，两者均判断得出隧道的变形具有持续增长的趋势，相互验证了彼此的准确性，也验证了本文思路的有效性。