连接器刚性插针接触对的插入力研究

(贵州航天电器股份有限公司，贵州贵阳，550009)

1　引言

本课题主要以刚性插针和弹性插孔为主要研究范围,插拔力是接触件机械性能里的一个重要指标，一个设计良好的接触件，其插入力和分离力应很接近。如果接触件结构尺寸设计不合理，会造成插入力急剧增大和连接器对接困难，甚至会损害接触件，影响机械性能里的机械寿命指标。本研究的主要目的就是要通过理论推算，找出影响插入力的主要因素，使设计接触件时能够避免不合理的结构尺寸，为插入力较大的连接器产品的改进提供参考。

2　圆形头刚性插针与开槽弹性插孔

2.1　插入力分析

圆头刚性插针的头部形状为半球形，开槽插孔是指在插头的插合端沿轴向加工一定数量的槽，形成多条弹性的悬臂梁，经收口等工序后形成弹性体，为防止插针与插孔对接时由于插针超差或歪斜造成插孔过量变形，通常在插孔外面的配置护管进行保护和导向。具体结构见图1。

图1　带护管直开槽弹性插孔与刚性插针

当刚性插针与直槽弹性插孔对接的时，我们以口部刚接触时的状态进行插入力受力分析，具体见图2。

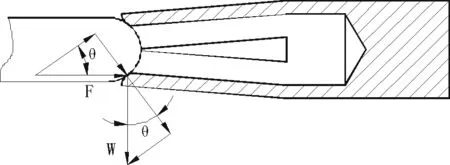
图2　插入力受力分析图

根据有摩擦的斜面施加水平推力公式可知：

F=Wta n(Φ+θ)

(1)

其中，F为插入力，W为插孔收口后的各花瓣的径向压力，Φ为摩擦角，θ为斜面的倾斜角。其中Φ=arctan(μ)，μ为摩擦系数。下面分析倾斜角θ的计算方法，具体见图3所示。其中，L为槽深，B为槽宽，d为插针直径，D为插孔孔径，α为收口后的弯曲角度，r为插孔孔口圆弧半径。根据三角函数关系可知：θ=arcos((h+r)/(d/2+r ))，h=D/2-k，k≈sinα*A , A≈L-r，α=arcsin(B/2/L)，将其代入公式(1)，由此可得:

F=Wtan(arctanμ+ arcos((D/2-B/2/L*(L-r)+r)/(d/2+r)))

(2)

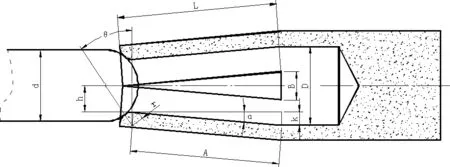
图3　倾斜角分析图

以下我们以20#插孔为例，其中已知L=5.5、B=0.4、D=1.12、d=1.02、r=0.2，通过改变其中的尺寸参数，重新计算插入力F，分析插孔各结构尺寸变化时对插入力的影响程度。

2.2　槽宽对插入力的影响

当L=5.5、D=1.12、d=1.02、r=0.2、W=1、μ=0.2时，改变B参数并运用公式(2)计算插入力，数据表见表1，折线图见图3。通过图表可知，槽宽与插入力成正比，随着槽宽的增加，插入力会显著增加。

图3　槽宽-插入力折线图

表1　槽宽-插入力数据表

2.3　槽深对插入力的影响

当B=0.4、D=1.12、d=1.02、r=0.2、W=1、μ=0.2时改变槽深L的参数，并运用公式(2)计算插入力，数据表见表2，折线图见图4。通过图表可知，槽深与插入力成正比，但是随着槽深的增加，插入力增加非常缓慢，由此可见，插孔插深对插入力影响非常小，可以忽略不计。

图4　槽深-插入力折线图

表2　槽深-插入力数据表

2.4　孔径对插入力的影响

当B=0.4、L=5.5、d=1.02、r=0.2、W=1、μ=0.2时改变孔径D的参数，并运用公式(2)计算插入力。数据表见表3，折线图见图5，通过图表可知，槽深与插入力成反比。

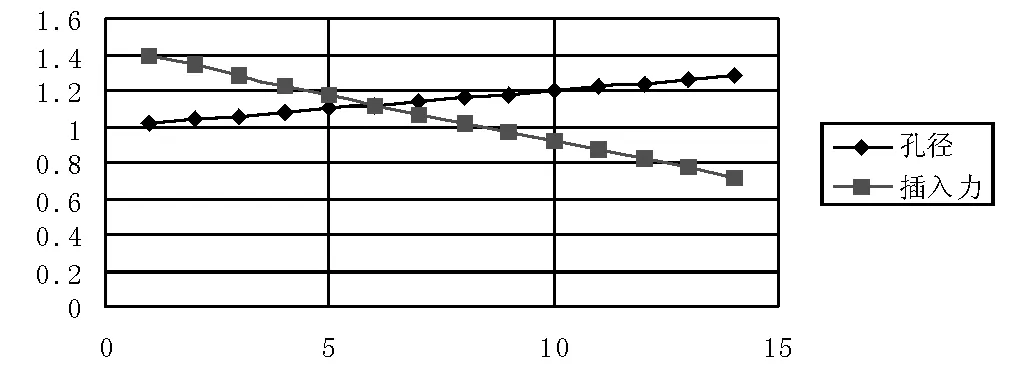
图5　孔径-插入力折线图

表3　孔径-插入力数据表

2.5　孔口圆弧半径对插入力的影响

当B=0.4、L=5.5、d=1.02、D=1.12、W=1、μ=0.2时，通过改变圆弧半径r的参数，并运用公式(2)计算插入力，数据表见表4，折线图见图6。通过图表可知，插孔孔口圆弧半径与插入力成反比。

图6　孔口圆弧半径-插入力折线图

表4　孔口圆弧半径-插入力数据表

2.6　花瓣径向压力对插入力的影响

当B=0.4、L=5.5、d=1.02、r=0.2、D=1.12、μ=0.2时，改变插孔收口后各花瓣的径向压力W，运用公式(2)计算插入力。数据表见表5，折线图见图7。通过图表可知，插孔径向力与插入力成正比，通常径向压力与插孔的分离力相关联，分离力的大小已经决定了径向力的大小，因此，径向力不能作为减少插入力的措施。

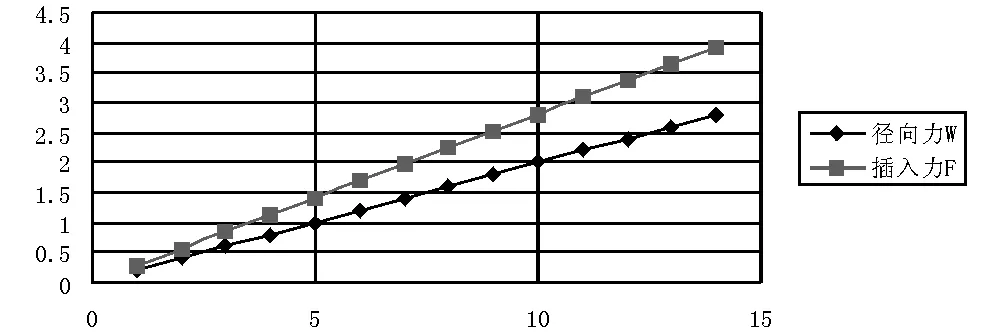
图7　插孔花瓣径向力-插入力折线图

表5　插孔径向力-插入力数据表

3　锥形头刚性插针与开槽弹性插孔

将刚性插针头部设计成锥形是接触件设计的一种常见手段，下面就对锥形头插针与开槽弹性插孔对接时的插入力进行受力分析，具体形状见图8。根据有摩擦的斜面推力公式 F=Wtan(Φ+θ)， F为插入力，W为径向力，Φ为摩擦角，θ倾斜角。其中Φ=arctan(μ)，μ为摩擦系数，由图可知，倾斜角θ=α/2，将以上关系代入公式(1)得出公式：

F=Wtan(arctan(μ)+α/2)

(3)

根据公式可知影响插入力的因素主要由插针头部锥度α、径向力W和摩擦系数μ。

下面就影响插入力的主要因素插针头部锥度α角进行研究，以径向力W=1，摩擦系数μ=0.2时，将其代入公式(3)进行分析，具体见表6和折线图见图9。由图表可知，插针头部锥度大小与插入力成正比，锥度越小插入力也就越小。

图8　锥形头插针与直槽弹性插孔受力分析图

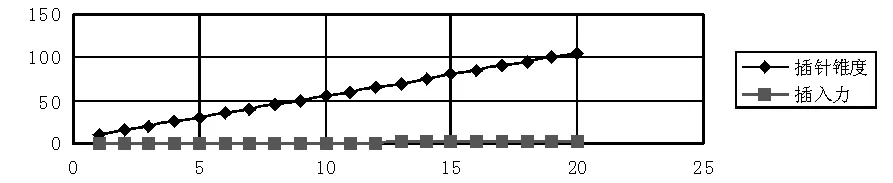
图9　插针锥度-插入力折线图

表6　插针锥度-插入力数据表

4　圆头刚性插针与喇叭口插孔

4.1　插入力分析

喇叭口插孔是将开槽插孔在收口过程中将插孔口部翻开，形成喇叭口形状，从而改善接触件对接状况，图10为喇叭口插孔的受力分析图。其对接方式类似锥形插针与开槽弹性插孔的对接，其插入力计算同样采用F=Wtan(Φ+θ)公式，其中Φ=arctan(μ)，μ为摩擦系数。

图10　喇叭口插孔受力分析图

下面分析斜面倾斜角的计算，具体见图11，其中A为喇叭口长度，B为槽宽，β为喇叭口弯曲角度， L为槽深，θ为斜面倾斜角，θ=β-α，α=arcsin(B/2/(L-A))，W为插孔花瓣的径向力,将以上关系代入公式(1)可得

F=Wtan(arctan(μ)+β- arcsin(B/2/(L-A)))

(4)

图11　喇叭口插孔倾斜角分析图

下面就以20插孔为例进行研究，假设插孔槽深L=5.5，槽宽B=0.4，喇叭口长度A=1，喇叭口弯曲角β=15°，插孔径向力W=1。

4.2　喇叭口插孔槽宽对插入力的影响

当L=5.5、A=1和β=15°时，通过公式(4)改变槽宽B的参数，分析其对插入力的影响。通过数据表(表7)和折线图(见图12)可知，插孔槽宽与插入力成反比，随着槽宽的增加，插入力缓慢的下降，因此槽宽对插入力的影响较小，可以忽略。

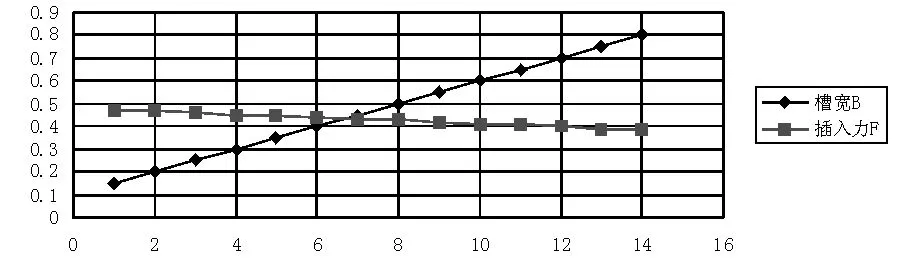
图12　喇叭口槽宽-插入力折线图

表7　喇叭口插孔槽宽-插入力数据表

4.3　喇叭口插孔槽深对插入力的影响

当B=0.4、A=1和β=15°时，通过改变槽深L参数，分析其对插入力F的影响。通过数据表(表8)和折线图(见图13)可知，插孔槽深与插入力成正比，随着槽深的增加，插入力缓慢的上升，因此槽深对插入力的影响较小，可以忽略。

图13　喇叭口槽深-插入力折线图

表8　喇叭口插孔槽深-插入力数据表

4.4　喇叭口翻口角度对插入力的影响

当B=0.4、A=1和L=5.5时，通过公式(4)改变翻口角度β参数，分析其对插入力的影响。通过数据表(表9)和折线图(见图14)可知，喇叭口翻口角度与插入力成正比，翻口角度的增加，插入力也快速上升，因此喇叭口翻口角度对插入力的影响较大，为喇叭口插孔的重要参数。

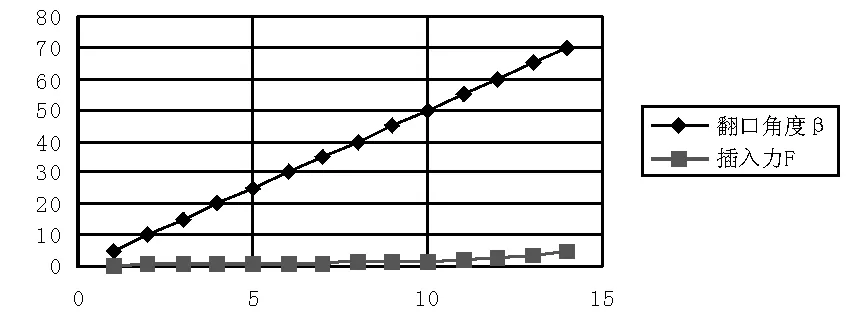
图14　喇叭口翻口角度-插入力折线图

表9　喇叭口翻口角度-插入力数据表

5　结束语

通过以上各种形状和尺寸的接触件的插入力分析，可以得出以下结论：

1)对于圆形头刚性插针与开槽弹性插孔接触件设计，可以通过减少切槽宽度、增大插孔孔径和增大孔口圆弧半径的方法有效降低插入力；

2)对于锥形头刚性插针与开槽弹性插孔接触件设计，可以通过减少插针头部锥形角度的方法，有效降低接触件的插入力；

3)对于圆头刚性插针与喇叭口开槽弹性插孔接触件设计，可以通过减小喇叭口翻口角度的方法使接触件的插拔力降低。

参考文献：

[1]机械设计手册. 机械工业出版社,2004.8.