基于概率的运载火箭控制系统设计方法研究

刘百奇，韦常柱，雷建长

(1.中国运载火箭技术研究院研究发展中心，北京 100076；2.哈尔滨工业大学，哈尔滨 150001)

0 引言

传统的运载火箭控制系统设计采用极限偏差设计方法，要求由各类随机偏差造成的干扰力矩在火箭飞行过程中不得超过控制系统的最大控制力矩，并且通过工程经验选取安全系数保证控制系统的最大控制力矩具有一定的冗余度。这种方法具有简单、可靠的特点，因此在工程实践中获得了良好的效果和广泛的应用。

但是随着认识的不断加深，研究人员发现由于各类干扰力矩的概率分布并不相同，运载火箭在不同飞行阶段，不同飞行方式和不同姿态下受到的干扰力矩情况也不相同。统一的安全裕度不能对系统的可靠性进行量化描述，为了追求安全可靠而增大余量或增加冗余度，造成了不必要的浪费和系统总体性能的下降[1-2]。

为解决安全系数法带来的问题，国内外学者开始探索将随机模型与数值方法结合以寻求数值方法的概率解决模式，基于概率的相关设计方法应运而生，并逐步在工程结构设计、热防护系统设计、飞行器控制系统设计、飞行器总体优化等领域得到了应用[2-4]。本文综述了基于概率的控制系统设计方法国内外研究现状，提出了基于概率的运载火箭控制系统设计流程及基于概率的控制器设计方法，并进行了初步的仿真验证。

1 概率控制国内外研究现状

国内外学者针对基于概率的控制系统设计的研究主要从两方面进行：一是系统偏差量统计建模方法，二是控制方法设计。

系统偏差量建模是指将系统不确定性因素按类型进行划分，采用概率模型量化系统偏差量。由于复杂系统的偏差量众多，在完成偏差量建模后，还需要采用灵敏度分析方法进行显著性分析，滤除对系统性能影响微弱的偏差量，以此降低概率设计的复杂度。

系统偏差量建模需要计算出偏差量所服从的概率密度函数(Probability Density Function, PDF)。目前对偏差量建模的方法通常有两种：一是通过对偏差量测量数据进行观察，在多个可能的分布中选择最合适的分布类型；二是通过对偏差量的产生机理进行分析，确定偏差量的分布类型。第一种方法的缺点在于需要大量的对比分析工作，而且很难保证所选定的概率分布能准确地反映偏差量试验数据的分布规律。第二种方法虽然从理论上来说比较准确，但在工程应用中，由于偏差量产生的原因十分复杂，除了个别简单系统，难以进行精确分析。

针对系统偏差量建模的问题，刘常青[5]研究了基于偏差数据分布已知/未知的、小样本/大样本数据的Bayes估计的统计建模方法。李宪东[6]基于最大熵原理确定PDF。Yen[7]利用Hopfield神经网络确定实验数据PDF类型的可行性，但并没有给出一般的拟合方法。Li 等[8]、汤保新[9]、Vidal等[10]分别利用Hermite正交多项式、Legendre正交多项式以及有理特征函数对给定PDF进行拟合，目的是用于计算有显式表达式的极限状态函数的失效概率。黄卓[11]利用混合Gamma分布建立了通用的试验数据PDF拟合方法。

在概率控制系统设计方面，主要的研究思路是基于输出PDF的闭环控制。1996年，Kárn等[12]将控制量描述为PDF形式，设计了控制器，但其仅具有数学理论上的正确性，因为仅关联控制量的PDF无法形成闭环控制回路。受此思想启发，Wang等[13-20]研究了基于标准输入量的控制输出PDF的方法，之后Wang等进一步深入研究了多种复杂控制输入形式下的输出PDF控制方法，并逐渐建立了输出PDF控制理论体系。继而，Wang及其研究团队[21]对基于PDF的控制系统稳定性和鲁棒性进行了分析，并研究了二次型目标输出PDF和实际输出PDF为指标时，一种解析紧凑的输出PDF控制形式。为了提高对随机控制系统模型的描述精度，以及对输出PDF神经网络描述的数值鲁棒性，Wang等[22]研究了根方B-样条描述方法以及分式B-样条描述方法等。此外，Forbes等[23]提出了过程PDF控制方法，由方程描述的平稳PDF的过程包含了完整的信息，既包括过程的动态信息，又包含了过程扰动的PDF。为实现对PDF误差的最小化控制，国外学者设计了多种控制算法，但这些算法对计算量的要求较高，难以获得工程应用。为了减小计算量、便于离线设计参数、降低设计参量维数，Guo等[24-25]研究了固定控制结构如PI或PID结构下的控制算法，并采用LMI方法对控制设计参数进行了求解。

当PDF不可测时，随机控制系统的目标则变为最小化闭环系统的不确定性和随机性。当控制系统的输入满足高斯分布特性且为线性时，可采用传统的最小变分方法进行控制系统设计。对于其他控制输入形式，则须对不确定性的一般测量状态进行分析，Yue等[26]基于最小熵原理进行了此种状态下的随机控制系统设计。

总体来说，国外对概率设计方法的研究相对于国内领先较多，在不同的行业领域应用广泛，且具有较为完整的一套设计规范和流程，而调研相关文献表明我国在概率设计领域研究较少，特别是在运载火箭概率控制系统设计领域，鲜见相关文献发表。

2 运载火箭控制系统概率设计基本思想及流程

概率设计法基本思想可以总结为对系统可靠度赋予概率定义，以系统的失效概率或可靠指标来度量系统的可靠度。在采用概率设计法进行系统可靠度分析时，必须首先明确系统的极限状态，即当系统的极限状态分布在某一部分超过某一特定状态后，不再满足设计规定的某一功能要求时，则此特定状态就称为该功能的极限状态。其次，概率设计需要对系统的极限状态进行评价，其在控制系统中可以表述为最大控制力矩大于干扰力矩的概率。因此，概率设计要求准确获得系统的极限状态并对其进行精确评价，进而衡量系统的可靠度，以此来评价概率设计结果的适用性。

在控制系统设计中，采用概率设计方法不仅能定量分析系统极限状态与可靠性之间的关系，还可以利用这种关系，建立安全系数与可靠度之间的规范，从而定量分析控制系统的控制能力需求，设计在概率层面上满足精度要求的控制系统，在保证一定可靠度下降低受干扰火箭的最大需求控制力矩，进而降低传统裕度安全设计中过大的系统冗余度,减少生产费用,降低系统复杂度，使控制系统更加精细化。

不同于传统极限偏差设计方法，由于其采用基于概率理论并通过统计分析的方式进行精细化设计，因此其设计过程相较于传统设计方法更加复杂。运载火箭控制系统概率设计的流程如图1所示。

由图1可知，运载火箭控制系统概率设计流程主要包括3部分内容:1)控制系统偏差精细化建模及分析；2)概率密度函数建模；3)基于密度函数成型的控制系统概率设计。其中，控制系统偏差精细化建模及分析主要是通过对偏差分布的精细化描述、蒙特卡洛打靶和灵敏度分析选取对火箭飞行影响较大的偏差因素及其分布，为后续设计提供基本条件并降低设计过程的复杂性；概率密度函数建模主要是通过拟合的方法得到蒙特卡洛打靶结果的分布，为后续概率密度函数成型控制提供基础；基于密度函数成型的控制系统概率设计主要是通过期望概率密度函数和输出概率密度函数的权值比较并基于稳定控制设计理论形成相应的控制律，最后通过需求控制力矩须大于干扰力矩来判断是否需要对控制器进行重新设计。

3 基于概率的控制器设计方法

(1)期望概率密度函数设计

考虑到火箭实际飞行过程中受到随机干扰的影响，控制器实际输出姿态角误差是概率分布的，这种情况可假设如图2所示。

图2中，Z表示控制器输出误差，且假设其服从正态分布，曲线为变量Z的概率密度函数曲线，其中，分布1和分布2表示为在相同随机干扰下，不同控制指令的输出误差分布，该误差分布可以看作是不同控制器或相同控制器在不同控制参数作用下的结果。分布1和分布2之间的关系为μ1=μ2=0，σ1>σ2。火箭姿态稳定的标志可以表述为Z≈0，或者说控制器输出误差在大概率下保持一个很小的范围。从图2中可以看出，分布2比分布1的变量Z在坐标原点附近的分布更加集中，因此控制器2的鲁棒性更强。

从上述讨论中可知，在进行火箭控制系统设计时，首先需要考虑的是设计期望输出姿态角误差的概率密度函数，即将期望输出角误差概率密度函数设计为μ=0，σ足够小的分布形式，然后通过设计合适的控制方法，使控制器输出的火箭姿态控制量u(k)(如舵偏、推力矢量等)能够使系统输出姿态角误差概率密度函数与期望输出角误差概率密度函数相符合。

(2)输出姿态角误差概率密度函数拟合

通过B样条概率密度函数拟合方法，火箭在随机复合干扰下的输出姿态角误差概率密度函数可表示为[13]：

e(y,U(k-1))

(1)

且

(2)

其中，Bi(y)为定义在多维区间[a,b]n上的多元基函数；Ω为由输出姿态角误差构成的空间；wi(k)为t=kT时刻输出姿态角误差概率密度函数的拟合权值，|e0|≤δ；y是控制系统输出，y∈[a,b]；μ(k)是采样时刻的控制输入；U(k-1)={μ(0),μ(1), …,μ(k-1)}，为系统t=kT时刻之前的控制输入，即该时刻的实际输出角误差概率密度函数γ(y,U(k-1))与过去的输入相关。

(3)概率系统状态空间

对于随机复合干扰作用下飞行的火箭而言，在不同推力矢量控制序列作用下输出姿态角误差概率密度函数不同，概率密度函数的拟合权值也不同。因此,拟合权值wi和姿态控制量μi之间存在动态关系，即

W(k+1)=AW(k)+Bu(k)

(3)

或

(4)

将式(2)代入式(4)得：

(5)

将式(2)代入式(1)得输出方程：

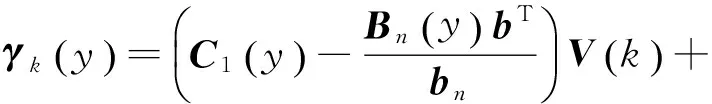
(6)

因此建立系统的状态空间为：

(7)

G、H、E需要由标准递推最小二乘法等辨识方法获得。

(4)系统矩阵辨识

考虑状态方程：

V(k+1)=GV(k)+Hu(k)

(8)

将其转化为如下形式：

(9)

式(9)为进行递推最小二乘法的标准形式，且

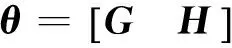
(10)

通过使用如下标准递推最小二乘算法：

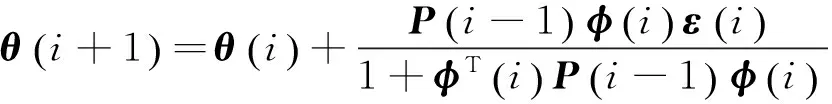
(11)

求出系统矩阵G和H，一般认为拟合精度足够，忽略拟合误差影响，则E可由式(12)求出：

(12)

(5)基于最优控制原理的概率控制器设计

为了通过推力矢量等控制序列μ(k)控制火箭在随机复合干扰下的输出姿态角误差概率密度函数，设期望输出角误差的概率密度函数为g(y)，系统的实际输出角误差概率密度函数为γ(y,U(k-1))，将拟合权值V(k)作为被控制量。将期望输出姿态角误差概率密度函数g(y)同样表示成B样条基函数拟合的形式：

g(y)=C(y)Vg+L(y)

(13)

则系统的控制量μ(k)应满足：

μT(k)Rμ(k)

(14)

式(14)为典型的LQR问题，可通过求解黎卡提方程得到：

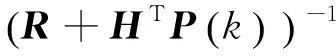
(15)

可得到满足控制要求的反馈控制律：

μ(k)=K(k)(V(k)-Vg)

(16)

其中，

K(k)=-(R+HTP(k+1))-1HP(k+1)G

上述μ(k)即是使输出概率密度函数与期望概率密度函数满足指标约束的最优控制量，将其直接作为火箭执行器的控制指令完成火箭的姿态控制。μ(k)的计算步骤为：

1)置k=1，在t=kT时刻采样求γ(y,U(k-1))；

2)通过B样条基函数拟合γ(y,U(k-1))得到V(k)；

3)根据姿态角误差精度要求设计g(y)，通过B样条基函数拟合g(y)得到Vg(k)；

4)通过标准递推最小二乘算法求θ、G、H、E；

5)根据式(16)计算μ(k)，k=k+1，返回a。

综上，基于最优控制的概率控制器结构如图3所示。

4 概率控制仿真分析

某运载火箭纵向运动的状态空间表达式为：

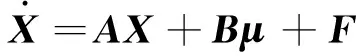
(17)

输出姿态角误差概率密度函数权值与控制量间的动态关系为：

V(k+1)=GV(k)+Hμ(k)

(18)

经过最小二乘方法辨识得到：

在初始时刻，姿态角误差的概率密度函数如图4所示，可以看出，在正态分布偏差F作用下，输出姿态角误差的分布比期望分布更加分散，控制的目的是使输出概率密度函数跟踪期望分布。

基于最优控制的控制器仿真结果如图5～图7所示。从图5可以看出输出姿态角误差概率密度函数在最优控制器作用下逐渐趋近于一个稳定的分布，从图6可以看出，输出姿态角误差概率密度函数的拟合权值与期望姿态角误差概率密度函数的拟合权值之差逐渐趋近于0，实现了对期望分布的跟踪，同时从图7可以看出，控制量趋向稳定，因此基于最优控制理论设计的控制器能够实现概率密度成型控制。

5 结论

本文综述了基于概率的控制系统设计方法的国内外研究现状，梳理了运载火箭控制系统概率设计的基本流程，并论述了基于概率的运载火箭控制系统设计方法，最后通过仿真验证了基于最优控制理论设计的控制器能够实现概率密度成型控制。表明通过概率密度函数成型控制的方法能够实现控制系统的精细化设计。但是，本文当前的研究只是初步验证了简单系统模型和价值函数的情况，后续还需结合运载火箭精细化模型，开展各类随机偏差影响分析及其概率密度函数建模，探索研究概率控制在运载火箭控制系统设计领域的工程实际应用价值，从而为我国运载火箭控制系统的精细化设计提供参考。

[1] 刘志全. 航天器机械可靠性特征量裕度的概率设计方法[J]. 中国空间科学技术, 2007, 27(4):34-43.

[2] 高显忠. 战术导弹概率设计与蒙特卡罗方法研究[D]. 长沙: 国防科学技术大学, 2009.

[3] Williams P. A Monte Carlo dispersion analysis of the X-33 simulation software[C]. AIAA Atmospheric Flight Mechanics Conference and Exhibit， 2001: 4067.

[4] Brandon J, Derry S, Heim G, et al. Ares-IX stability and control flight test: analysis and plans[C]. AIAA SPACE 2008 Conference & Exposition, 2008: 7807.

[5] 刘常青. 基于概率偏差的战术导弹总体方案设计技术[D]. 长沙: 国防科学技术大学, 2011.

[6] 李宪东. 基于最大熵原理的确定概率分布的方法研究[D]. 北京: 华北电力大学, 2008.

[7] Yen E C. Is taking natural log superior to not?-Using a characteristics oriented fuzzy Hopfield neural network to identify probability density functions[J]. Expert Systems with Applications, 2009, 36(3): 5094-5099.

[8] Li X B, Gong F Q. A method for fitting probability distributions to engineering properties of rock masses using Legendre orthogonal polynomials[J]. Struc-tural Safety, 2009, 31(4): 335-343.

[9] 汤保新. 正交多项式拟合概率密度函数在可靠度计算中的应用[J]. 泰州职业技术学院学报, 2006, 6(1):40-44.

[10] Vidal J, Bonafonte A, Fernández N. Rational characteristic functions and Markov chains: application to modeling probability density functions[J]. Signal Processing, 2004, 84(12): 2287-2296.

[11] 黄卓, 李苏军, 郭波. 基于混合Gamma分布的通用可靠性寿命数据拟合方法[J]. 航空学报, 2008, 29(2):379-386.

[13] Wang H. Bounded dynamic stochastic systems: mode-lling and control[M]. Springer Science & Business Media, 2012.

[14] Wang H. Robust control of the output probability density functions for multivariable stochastic systems[C]. IEEE Conference on Decision and Control, 1999, 2:1305-1310.

[15] Baki H, Kabore P, Wang H. A new approximation for the modeling and control of bounded stochastic distributions[C].UKACC International Conference on Control 2000,2000.

[16] Afshar P, Nobakhti A, Wang H. Direct solution of the parametric Stochastic Distribution Control pro-blem[C]. IEEE Conference on Decision & Control, 2010: 2616-2621.

[17] Wang H. Complex Stochastic Systems Modeling and Control via Iterative Machine Learning[C]. IEEE International Conference on Engineering of Intelligent Systems, 2006, 71 (13-15) :2685-2692.

[18] Afshar P, Wang H. ILC-based adaptive minimum entropy control for general stochastic systems using neural networks[C]. IEEE Conference on Decision and Control, 2008: 252-257.

[19] Afshar P, Yue H, Wang H. Robust iterative learning control of output PDF in non-Gaussian stochastic systems using Youla parametrization[C]. American Control Conference, 2007: 576-581.

[20] Afshar P, Wang H, Chai T. An ILC-based adaptive control for general stochastic systems with strictly decreasing entropy[J]. IEEE Transactions on Neural Networks, 2009, 20(3): 471-482.

[21] Wang A, Wang Y, Wang H. Shape control of conditional output probability density functions for linear stochastic systems with random parameters[J]. International Journal of Systems, Control and Communica-tions, 2011, 3(1): 82-94.

[22] Wang H, Afshar P. ILC-based fixed-structure controller design for output PDF shaping in stochastic systems using LMI techniques[J]. IEEE Transactions on Automatic control, 2009, 54(4): 760-773.

[23] Forbes M G, Forbes J F, Guay M. Regulatory control design for stochastic processes: shaping the probability density function[C]. American Control Conference, 2003, 5: 3998-4003.

[24] Guo L, Wang H. Pseudo-PID tracking control for a class of output pdfs of general non-gaussian stochastic systems[C]. American Control Conference, 2003, 1: 362-367.

[25] Guo L, Wang H. PID controller design for output PDFs of stochastic systems using linear matrix inequalities[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2005, 35(1): 65-71.

[26] Yue H, Zhou J, Wang H. Minimum entropy of B-spline PDF systems with mean constraint[J]. Automatica, 2006, 42(6): 989-994.