垂直起降可重复使用运载器发展现状与关键技术分析
2018-04-17崔乃刚韦常柱徐大富
崔乃刚,吴 荣,韦常柱,徐大富,张 亮
(1. 哈尔滨工业大学航天工程系,哈尔滨 150001;2. 上海宇航系统工程研究所,上海 201108)
0 引言
多级火箭是目前人类进入空间的主要手段,但现役的多级运载火箭仍存在一定不足:单发火箭生产与测试周期较长,发射密度难以突破,无法满足快速响应发射需求;火箭的箭体和箭上设备总质量占比较小,但其价格占比极高,火箭完成任务后便抛弃箭体与设备,一次性使用导致成本高昂;火箭弃用残骸落点分布较大,内陆发射对落区人员生命和财产安全构成一定威胁,而海上发射则存在引发国际争端的风险。
为突破传统运载火箭的局限性,可重复使用运载器(reusable launch vehicle,RLV)的概念逐渐产生并受到业界的重视。相对于传统一次性运载火箭,可重复使用运载器是指运载器从地面起飞完成预定发射任务后,全部或部分返回并安全着陆,经过检修维护与燃料加注后,可快速再次执行发射任务[1]。箭体和设备的多次可重复使用分摊了全寿命周期成本,可有效降低运载器的单次使用成本。根据不同标准,可重复使用运载器有多种分类[2],按起降方式可划分为:垂直起飞/水平降落(vertical takeoff horizontal landing,VTHL)、水平起飞/水平降落(horizontal takeoff horizontal landing,HTHL)和垂直起飞/垂直降落(vertical takeoff vertical landing,VTVL)等。
相较于其他两种方案,垂直起飞/垂直降落(垂直起降)运载器以火箭发动机作动力,采用传统火箭外形并进行小幅改动(增加着陆缓冲机构、栅格舵等),无需新研外形及相关火箭系统,也无需增加复杂热防护和翼舵等结构机构,可在较小面积平面进行垂直着陆,无需长距离的大型跑道,技术跨度较小,研发成本较低[2]。近年来,SpaceX等航天公司推出的低成本垂直起降运载器成功实现了垂直回收并复用[2-4],垂直起降已被证明是一种可行的技术途径,在商业航天发射市场具有较强的竞争力,在未来月球、火星等行星际探测中也具有广泛的应用前景。
本文针对垂直起降可重复使用运载器,首先介绍其研究现状,然后着重分析垂直起降运载器涉及的关键技术,最后给出垂直起降运载器的发展趋势。
1 垂直起降运载器发展现状
垂直起降运载器的概念从20世纪60年代提出开始,就受到各国航天机构以及私营航天公司的高度重视,诞生了多种适应于不同星体(不同引力环境)的垂直起降运载器方案及试验飞行器。
1.1 ROOST/ROBUS
20世纪60年代,美国道格拉斯飞机公司(Douglas Aircraft Company,现已并入波音)的工程师Philip Bono提出了可重复使用垂直降落单级入轨运载器的概念[5],是垂直起降运载器的先驱。ROOST(Recoverable One Stage Orbital Space Truck)和ROMBUS[6](Reusable Orbital Module, Booster, and Utility Shuttle)是其中的代表,ROMBUS的助推器通过降落伞回收,芯级通过发动机反喷和降落伞减速并展开着陆缓冲机构实现垂直软着陆。
1.2 Apollo Lunar Module
20世纪60年代,为实现载人登月并返回地球,美国阿波罗计划设计了月球垂直起降两级飞行器——阿波罗登月舱(Apollo Lunar Module)[7-8]。阿波罗登月舱由下降级和上升级组成,通过下降级火箭垂直软着陆在月球表面,任务完成后上升级与下降级分离,上升级发动机点火垂直起飞离开月球。随着1969年阿波罗11号的成功登月并返回,垂直起降运载器概念得到工程验证。
1.3 DC-X/DC-XA
经过一系列垂直起降运载器方案的研究后[5],20世纪90年代,麦道公司(McDonnell Douglas,现已并入波音)根据美国国防部战略防御计划组织需求研究了一款单级入轨运载器,并在研究第2阶段生产了1∶3缩比试验飞行器DC-X(Delta Clipper-Experimental,三角快帆)[9-11],如图3(a)所示。DC-X共有4台液氢液氧发动机,于1993年首飞,到1995年共进行8次飞行试验,验证了起飞、悬停、机动、着陆等性能。在第8次飞行试验中,由于故障DC-X以约4.27m/s速度硬着陆导致外壳损坏。DC-X的飞行试验情况如表1所示。

日期持续时间/s高度/m状态1993.08.185946成功1993.09.116692成功1993.09.3072370成功1994.06.20136870成功1994.06.2778790成功1995.05.161241330成功1995.06.121321740成功1995.07.071242500失败
1995年,美国国家航空航天局(NASA)对DC-X的发动机、贮箱、材料等进行了改进,改进后的试验飞行器成为DC-XA(Delta Clipper-Experimental Advanced)[12-13],如图3(b)所示。DC-XA在1996年共进行了4次飞行试验,其中第2次和第3次飞行间隔时间仅26h;在第4次飞行试验中,由于2个着陆架未展开,着陆失败导致爆炸。后续由于缺乏资金,项目终止。DC-XA飞行试验情况如表2所示。

表2 DC-XA飞行试验表
1.4 RVT
1998年日本宇宙航空研究开发机构(JAXA)提出了可重复使用飞行器测试(Reusable Vehicle Testing,RVT)项目,对发动机、快速复用、高性能、轻量化结构和材料等关键技术进行验证[14-18]。如图4所示,RVT试验样机外形与DC-X相似,同样具有4个着陆腿,但仅采用1台液氢液氧发动机,到2009年RVT共进行14次测试。
1.5 XA-0.1系列
2009年,Masten Space Systems公司设计的Xombie/Xoie垂直起降火箭试验平台在由NASA发起的Lunar Lander Challenge竞赛中取得优胜,并在此基础上开发了Xaero/Xodiac等XA-0.1系列垂直起降火箭试验平台[19]。Masten公司垂直起降可重复使用火箭的情况如表3和图5所示。通过研究垂直起降火箭技术,Masten公司的首要目标是实现无人亚轨道航天飞行,最终目标是能够支持轨道航天器发射。

表3 Masten公司垂直起降可重复使用火箭
1.6 New Shepard/New Glenn
2000年创立的蓝色起源公司Blue Origin着重研究用于亚轨道和轨道空间发射的垂直起降火箭,从而大幅降低发射成本,提高可靠性,以提供私人太空旅行服务。2015年11月23日,该公司成功发射采用BE-3发动机(液氢液氧)的亚轨道火箭New Shepard(100.5km高度),并成功实现助推级的垂直软着陆,首次完成亚轨道垂直起降RLV助推级的发射和定点垂直软着陆回收[2-3]。2016年1月22日,回收的助推级再次发射(101.7km高度)并成功定点垂直软着陆,率先完成亚轨道垂直起降RLV助推级箭体的回收后再次复用。2016年4月2日、2016年6月19日和2016年10月5日,同一箭体进行了第3次、第4次和第5次(最后1次)发射并成功回收。New Shepard的发射与着陆情况如图6所示。
Blue Origin于2016年9年公布了其正在研发的下一代垂直起降可重复使用火箭——New Glenn[3]。New Glenn用于执行轨道发射任务,近地轨道(LEO)有效载荷为45t,箭体直径为7m,分为两级(箭长82m)和三级版本(箭长95m)。一级采用7台BE-4发动机(液氧甲烷),二级采用7台BE-4 Vacuum发动机(液氧甲烷),三级采用一台BE-3U发动机(液氧液氢),计划于2020年首次发射(见图7)。与New Shepard类似,New Glenn的助推级垂直起降可重复使用。
1.7 Falcon系列
SpaceX是2002年建立的私人航天公司,旨在降低空间运输成本和火星移民,已经成功发展Falcon(猎鹰)系列运载火箭和Dragon(龙)系列飞船,提供地球轨道发射服务[20]。
在其首款两级液体运载火箭Falcon 1的基础上,SpaceX推出了两级液体运载火箭Falcon 9 v1.0,一子级采用9台Merlin-1C液氧煤油发动机(3×3构型,如图8(a)),二子级采用1台Merlin-1C真空版,于2010年首飞。火箭一子级预留降落伞安装空间。在最早的两次飞行试验中,由于箭体无法承受无控再入大气的气动载荷导致开伞前解体,SpaceX放弃了伞降方案并转向垂直起降技术[2]。2011年该公司公布了可重复使用运载系统发展计划(SpaceX reusable launch system development program),该计划的长期目标是实现火箭1、2级的快速垂直回收,并在数小时内再次发射。
蚱蜢(Grasshopper)是SpaceX第一款垂直起降试验飞行器[21],采用1台Merlin-1D发动机,如图9(a)所示。Grasshopper于2012年9月~2013年10月共进行了8次飞行试验,最大飞行高度为744m,最大横移为100m(见表4),测试了火箭垂直起降必需的变推力控制、精确导航、制导和控制等技术。
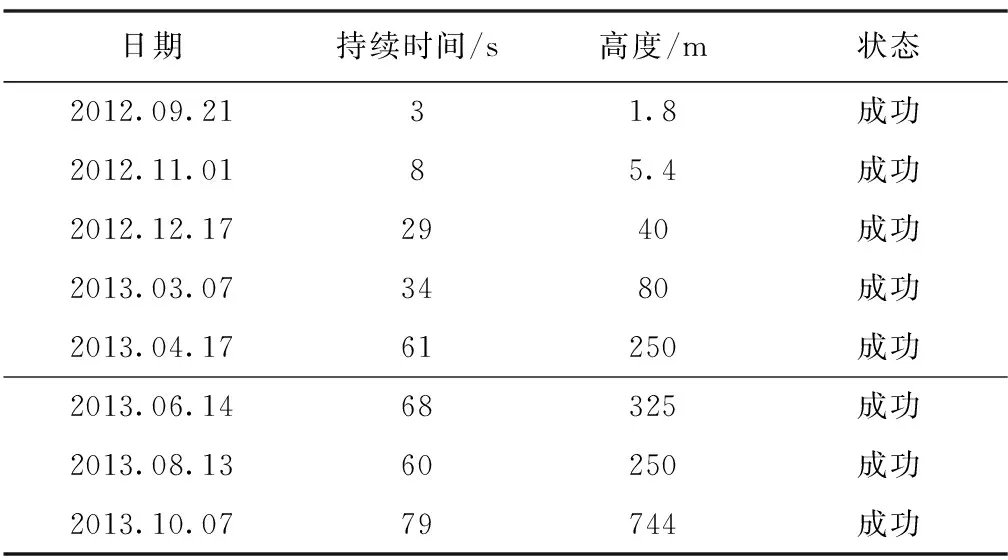
日期持续时间/s高度/m状态2012.09.2131.8成功2012.11.0185.4成功2012.12.172940成功2013.03.073480成功2013.04.1761250成功2013.06.1468325成功2013.08.1360250成功2013.10.0779744成功
在v1.0的基础上SpaceX升级推出了Falcon 9 v1.1,一子级采用9台Merlin-1D液氧煤油发动机(Octaweb构型,如图8(b)),安装有垂直返回的栅格舵和着陆腿,二子级采用1台Merlin-1D真空版,最大箭长为68.4m(一子级为42.6m),直径为3.66m,于2013年首飞。同期,采用v1.1一子级贮箱的垂直起降试验飞行器F9R Dev(Falcon 9 Reusable Development Vehicles)于2014年4月首飞[21],于第3次测试安装了栅格舵,如图9(b)所示。到2014年8月F9R Dev1共进行4次飞行试验,最大高度为1000m,第4次由于传感器故障爆炸。后续为进行更高飞行能力测试的F9R Dev2于2015年2月19日被停止。在开展F9R Dev试验的同时,SpaceX开始进行Falcon 9发射任务后一子级返回的飞行试验[22-23]。
(1)海面软接触测试(Falcon 9 v1.1)
Falcon 9 v1.1共进行5次(2013年9月29日失败,2014年4月18日、2014年7月14日、2014年9月21日、2015年2月11日成功)海面软接触飞行试验,控制一子级垂直软接触海面,见图10(a)。
(2)软着陆测试(第1阶段,Falcon 9 v1.1)
Falcon 9 v1.1 于2015年1月10日、2015年4月14日和2016年1月17日在无人海上着陆平台进行了海上软着陆飞行测试,均告失败,见图10(b)。
在v1.1版的着陆失败经验上,SpaceX进一步改进发展了Falcon 9 v1.2(Full Thrust,FT),一级发动机更换为9台Merlin-1D改进型,二级采用1台Merlin-1D真空版改进型,最大长度为70m,于2015年12月首飞。
(3)软着陆测试(第2阶段,Falcon 9 v1.2)
基于Falcon 9 v1.2,SpaceX开展第2阶段的软着陆测试:2015年12月22日,第1次地面回收成功,见图11(a);2016年4月8日,第1次海上回收成功;2017年3月30日,一子级首次成功复用并海上回收成功,见图11(b)。截至2017年12月,Falcon 9 v1.2的发射情况如表5所示。

日期(UTC)一子级编号载荷质量/kg目标轨道状态任务回收2015.12.22B10192034LEO成功地面成功2016.03.04B10205271GTO成功海上失败2016.04.08B1021.1*3136LEO成功海上成功2016.05.06B10224696GTO成功海上成功2016.05.27B1023.13100GTO成功海上成功2016.06.15B10243600GTO成功海上失败2016.07.18B1025.12257LEO成功地面成功2016.08.14B10264600GTO成功海上成功2016.09.01B10285500GTO发射前爆炸计划海上2017.01.14B1029.19600LEO成功海上成功2017.02.19B1031.12490LEO成功地面成功2017.03.16B10305600GTO成功未进行2017.03.30B1021.25300GTO成功海上成功2017.05.01B1032.1未公开LEO成功地面成功2017.05.15B10346070GTO成功未进行2017.06.03B1035.12708LEO成功地面成功2017.06.23B1029.23669GTO成功海上成功2017.06.25B1036.19600LEO成功海上成功2017.07.05B10376761GTO成功未进行2017.08.14B1039.13310LEO成功地面成功2017.08.24B1038.1475SSO成功海上成功2017.09.07B1040.14990+LEO成功地面成功2017.10.09B1041.19600LEO成功海上成功2017.10.11B1031.25200GTO成功海上成功2017.10.30B1042.13500GTO成功海上成功2017.12.15B1035.22205LEO成功地面成功2017.12.23B1036.29600LEO成功海面软接触
在此期间,SpaceX的龙飞船垂直软着陆回收试验计划也在2014年5月公布,飞行试验平台为蜻蜓(DragonFly),如图12所示。2017年7月,由于认证问题,龙飞船垂直软着陆计划被宣布取消[24]。
基于Falcon 9捆绑两个相同的垂直起降一子级(见图13),SpaceX的下一代重型运载火箭Falcon Heavy于2018年2月6日首飞成功[3]。
在2017年国际宇航大会上,SpaceX公司公布了其火星移民计划及对应的运载器BFR(Big Falcon Rocket),其一、二级均可垂直着陆并可重复使用[25]。
1.8 其他
其他一些机构和公司也设计并试验了一些垂直起降运载器试验平台,包括Rotary Rocket Company(已破产)的Rotary Rocket、Armadillo Aerospace(资产被Exos Aerospace收购)的Super Mod和Stig,以及NASA的Mighty Eagle Lander和Morpheus Lander等,见图15。
2 垂直起降运载器关键技术
垂直起降运载器的研究与应用涉及变推力可重复使用发动机技术、高可靠着陆缓冲机构技术、快速检修维护技术、轻量材料与结构、轨迹设计与导航、制导控制等多项关键技术[2]。对于运营阶段的垂直起降运载器,其设计状态已经基本固定,轨迹设计与导航、制导控制系统是运载器完成发射任务并安全精确返回的关键。典型的垂直起降运载器在完成上升段飞行后,其返回过程中将经历调姿段、修航段、高空滑行段、动力减速段、大气减速段和垂直着陆段等多个飞行段,飞行空域和速域广、发动机多次开关机、飞行环境复杂多变,内外扰动及不确定性强。本文将结合垂直起降运载器的特点,重点分析其在垂直起降过程中的轨迹设计与导航、制导控制存在的问题,进而总结垂直起降运载器需要解决的关键技术,并提出相应的解决途径。
2.1 轨迹设计与优化技术
对于投入运营阶段的运载器而言,轨迹设计与优化是在相对固化设计状态下,提高飞行器性能的有效途径之一。相对于一次性使用的运载器,垂直起降运载器在优化设计飞行轨迹时,既要满足发射任务入轨要求,又要确保运载器能够垂直安全软着陆于指定着陆场,其返回段飞行与上升段飞行紧密耦合。垂直起降运载器的上升段和返回段均以推力为主要控制方式,在同等推力条件下,燃料分配决定了运载能力和返回能力。在优化设计垂直起降运载器轨迹时,需要同时满足上升段、返回段各项基本约束,并权衡上升段和返回段的性能指标。
对于垂直起降运载器的轨迹设计与优化问题,在建立全程轨迹优化模型后,采用双层优化策略[26-27]进行最优轨迹求解是一种可行的技术途径。在双层优化策略中,首先使用例如凸优化[28]等具备较快收敛速度和较好全局性的方法求解得到“热启动”初值解,然后在此基础上采用例如伪谱法[29]等离散精度较高的方法寻求精确最优解。进一步根据优化结果进行参数敏感性分析、约束裕度分析和性能指标分析,进而调整约束模型和性能指标模型,针对调整后的模型再次进行优化,多轮迭代后即可得到垂直起降运载器可行最优轨迹解。
2.2 返回高精度导航技术
垂直起降运载器返回飞行过程中经历多个飞行段,各飞行段工作环境和导航需求不同,对导航精度尤其是着陆段导航精度要求较高,仅依靠惯性/卫星的组合导航系统显然无法满足要求。因此,返回段全程在采用惯性/卫星组合导航的基础上,需要结合不同飞行段的特点、可用信息源、导航要求等设计分段导航方案。其中,垂直着陆段高精度导航系统为关键之一,对导航姿态精度、位置精度(水平及高度)、速度精度要求极高。此时运载器距着陆场较近,相对着陆场表面速度较低,便于采用各种辅助导航手段,但是运载器尾部需对准着陆场,而且发动机处于工作状态,导航设备的安装、使用条件受到较大限制。而着陆段之前的各飞行段,也需要尽可能提高导航精度,为制导控制系统提供较好的载体状态信息以保证后续飞行段具有较高的交接精度。
对于修航段、调姿段和高空滑行段,由于运载器处于稠密大气层外,可引入天文导航[30-32]提高导航精度;动力减速段,运载器已进入大气层,在结合天文导航时需要考虑环境扰动[33];大气减速段中前期,可结合视觉辅助[34-36]等多种相对导航手段及其组合形式;大气减速段后期和垂直着陆段,可引入激光雷达[37-39]、卫星导航地面差分站[40-42]等辅助手段。其中,差分卫星导航设备体积小,质量小,安装和使用限制小,定位精度高,自主性和适应性强,无需向外发送信息,并可全天候工作,是提高垂直起降运载器着陆段导航精度的有效手段,并且也可应用于接近着陆场的其他飞行段导航。但差分卫星导航也存在导航精度高度依赖地面基站,且运载器上单台卫星导航设备无法定姿的缺陷。其他导航方法在安装设备时需考虑设备的观测条件和安装位置,在垂直着陆段由于发动机喷气尾焰等干扰将无法使用。综上所述,垂直起降运载器返回全程高精度导航系统的设计需要综合考虑导航精度、设备质量以及使用环境的限制。
2.3 返回高精度制导技术
垂直起降运载器在返回过程中飞行剖面复杂,发动机两次开关机、长时间无动力再入,主动段关机点偏差以及多种内外扰动将严重影响返回制导精度,传统运载器采用的开环或跟踪制导等方法将无法满足精确垂直软着陆制导需求。考虑到调姿段和高空滑行段位于稠密大气层外且发动机关机,无制导飞行能力,因此本文将分别分析修航段、动力减速段、大气减速段和垂直着陆段的制导问题。
(1)修航段
由于垂直起降运载器为传统的火箭构型,进入大气后,升力不足以进行大范围机动,运载器的落点位置与修航段关机终端状态密切相关,而修航段终端状态可确定唯一的虚拟绕地椭圆轨道,因此修航段制导可认为是以标称修航段终端为虚拟轨道入轨目标点的精确入轨问题,针对此类问题目前可采用跟踪制导[43]、迭代制导[44-47]等方法。在实际应用中,由于虚拟轨道相对于着陆场静止,受到地球自转的影响,在迭代制导指令求解中偏航角小扰动假设不成立,因此需要考虑偏航角的影响。考虑到运载器在主动段关机时可能存在的大偏差,对于大偏差条件下的椭圆轨道入轨问题,目前迭代制导中的入轨点迭代更新等方法虽然能够显著地提高制导精度,但引入的迭代计算将增加箭载计算机工作负荷[47],不利于在线实现。因而可利用椭圆轨迹坐标与基准坐标轴之间的几何关系进行入轨目标点在线更新,从而提高修航段虚拟入轨制导精度。
(2)动力减速段
进入大气后,动力减速段运载器发动机点火,为避免再入大气过程中法向过载和动压过大,发动机推力方向与速度矢量方向相反进行制动减速,在地球引力作用下进行重力转弯(gravity turn)[48]。目前重力转弯制导的典型方法是根据重力转弯得到标称弹道,进而设计跟踪制导律实现对参考弹道的跟踪[48-57]。但是上述方法主要应用于无/稀薄大气的地外星体探测任务中,对于垂直起降运载器的动力减速段,在多变气动特性及外部干扰时难以保证高精度的轨迹跟踪。
自适应动态面标称轨迹跟踪方法[58-60]是一种将路径跟踪与自适应动态面控制方法相结合的强鲁棒、抗干扰、高精度自适应跟踪制导律。该方法基于反步法(backstepping)设计双层动态面:位置面根据标称位置产生期望速度并经过1阶低通滤波消除抖振后传递给速度面,而速度面跟踪期望速度产生制导指令。对于制导过程中存在的偏差扰动,通过在各动态面引入观测器估计扰动并补偿,进而提高了制导系统的抗干扰能力。算法整体结构简洁,便于工程实现,对垂直起降运载器动力减速段的重力转弯跟踪制导是一种可行的技术途径。
(3)大气减速段
在大气减速段发动机关机,垂直起降运载器利用栅格舵作为执行机构制导箭体以一定的落角飞行至着陆场上空预定位置。对于一子级等传统欠升力轴对称外形的无动力大气再入制导问题,一般采用标称轨迹跟踪制导方法和预测校正制导方法等[61-63],但上述方法均难以对终端落角进行有效约束。因此,对于垂直起降运载器大气减速段这类包含终端角度约束的制导问题,可应用偏置比例导引[64]、变系数比例导引[65]、最优制导律[66]、滑模制导律[67]等终端角度约束制导方法[68]。
(4)垂直着陆段
垂直着陆段运载器飞行环境高动态变化,着陆过程中制导律给出推力矢量方向、推力大小和发动机工作时间,使运载器抑制扰动偏差影响并精确垂直软着陆于预定位置,这种依赖矢量推力反推并考虑位置、速度和姿态约束的垂直着陆制导问题即为动力下降制导问题[69]。由于重力转弯方法控制结构简单易于实现,在早期的月球探测器任务中被成功应用于垂直着陆段制导中,但其难以实现精确定点着陆。在阿波罗计划中,阿波罗登月舱应用多项式制导方法成功实现月面垂直软着陆[69-71],我国嫦娥三号着陆器则采用改进多项式制导算法成功实现了月面垂直软着陆[37]。该算法将着陆器标称加速度拟合成关于飞行时间的多项式函数,而制导时间可根据着陆器初始点和期望终端状态解析求解,但这种方法并非燃料最优的,且无法约束推力大小的上下界,指令推力大小可能超出发动机的能力。对于地球着陆问题,由于大气作用不可忽略,可能会导致无法得到解析解,多项式制导等方法并不适用于大气环境中的垂直软着陆任务。
近年来随着计算技术和优化理论/算法的发展,基于在线轨迹优化的最优制导成为可能。基于在线优化的闭环制导方法具有处理约束能力强、同时能够保证最优性和鲁棒性等优点。凸优化方法[72-77]具有求解快速性和确定性的优点,且良好设计的凸优化算法计算精度与基于NLP(nonlinear programming)的优化算法相当,具备发展为在线轨迹优化方法的潜力,其中基于凸优化方法开发的G-FOLD制导程序在Masten公司Xombie垂直起降试验平台的飞行试验中已经取得了成功[78]。
利用凸优化方法快速性的优点,可将其嵌入到模型预测框架中,以较高频率滚动时域优化的方式构成隐式闭环,将每个轨迹优化周期内的轨迹偏差以状态采样的方式馈入轨迹优化计算,新生成的控制量即是以当前实际状态为起点的最优解。随着轨迹优化更新频率的提高,制导误差也将随之减小。若算法计算效率满足要求,则可将基于凸优化的在线闭环制导拓展到垂直起降运载器的返回全程。
2.4 返回飞行控制技术
垂直起降运载器返回过程中贮箱内剩余燃料较少,在运载器自身运动和外部干扰等影响下更易发生液体晃动,尤其是在调姿段,运载器大幅调姿将导致贮箱内液体大幅晃动,这将对运载器的姿态控制造成不良影响,必须在返回飞行控制中加以考虑。
目前工程上在建立运载器动力学模型时一般采用简化机械模型对液体晃动进行等效处理,包括等效单摆、等效球摆和等效弹簧振子等[79-82]。上述的等效力学模型能够有效地反应液体小幅晃动的动力学特性,但对于调姿段的大幅非线性液体晃动问题并不适用。对于大幅晃动问题,已有的研究包括质心面模型[83-85]、运动脉动球模型[86-91](moving pulsating ball model,MPBM)等大幅晃动等效力学模型。运动脉动球模型将贮箱等效为球形贮腔,贮箱内液体等效为一个质量相同半径可变的均匀球体且始终与球形腔内壁存在一个瞬时接触点,在欧空局微重力液体晃动特性研究实验卫星Sloshsat FLEVO项目中得以应用和验证[92-93]。
为进行垂直起降运载器控制系统设计,建立等效力学模型时会进行适当的近似,造成等效模型与箭体真实状态存在一定偏差,这些未建模动态和模型偏差等不确定性将对运载器的姿态控制造成一定影响。在返回过程中,运载器反向再入大气,气动外形的不规则增加了气动参数的不确定性;由于火箭需面对任务多变的快速发射需求,其返回时的风场数据难以准确获得,穿越高空风区时细长的箭体受到未知风切变的干扰导致箭体不同位置受到的风载不一致;箭体结构偏差、安装偏差、弹性、晃动与气动耦合等未建模动态和内外扰动均将严重影响运载器姿态稳定性。传统固定系数校正网络和PID控制结构难以保证模型不确定性和外部复杂干扰下的控制需求。由于模型不确定性和外部扰动难以测量,因而在垂直起降运载器的控制系统设计中,可采用扰动观测器估计扰动(将模型不确定性和外部扰动视为整体),并根据估计值在控制器中补偿以抑制扰动的影响,这种方法已在工业界得到广泛应用,被称为基于扰动观测器的控制方法(disturbance observer based control,DOBC)[94]。扰动观测器是DOBC的核心之一,目前已发展的观测器包括高增益观测器[95]、鲁棒观测器[96]、扩张状态观测器[97-98]、滑模观测器[99-102]等;在DOBC的控制器设计中,可采用的控制方法包括自抗扰控制[103-105]、滑模控制[106-110]等。
垂直起降运载器在返回过程中使用矢量发动机、栅格舵和RCS多种执行机构,在返回飞行控制系统设计中需要研究多执行机构复合控制技术[111-112]。由执行机构特性可知,发动机和栅格舵工作连续,而RCS系统工作离散,需要将控制系统输出的力矩控制指令在执行机构间进行分配,进而解算各执行机构控制信号[113]。针对多执行机构控制分配问题,目前已发展了伪逆法[114]、直接分配法[115]、链式法[116]、线性规划[117]等线性控制分配方法,以及分段线性规划[118]、二次规划[119]、序列二次规划[120]等非线性控制分配方法,其他还包括自适应控制分配方法[121]、智能控制分配方法[122]等。线性控制分配方法目前研究和应用较为广泛,但在实际飞行器系统中,执行器操纵量与其产生的控制力之间存在非线性,线性控制分配方法存在不足,可用非线性控制分配方法,但目前的非线性控制分配方法存在计算量大的缺陷,难以实际应用于飞行器系统中,因此需要进一步研究高效、精确的非线性控制分配方法[123]。
由于垂直起降运载器执行机构复杂,返回过程中可能出现偏移、卡死、失效等执行机构故障,为保障运载器在故障情况下仍能安全运行并保持精度,进行飞行器的容错控制(fault-tolerant control,FTC)方法研究十分必要[124-125]。容错控制主要分为基于鲁棒控制技术的被动容错方法和基于故障补偿技术的主动容错方法,被动容错方法对于维数较低、故障源较少的系统有较好的应用,但对于维数高、故障源较多的复杂系统,一般采用主动容错方法[126-127]。根据是否需要精确估计故障信息,主动容错方法主要分为基于故障检测与分离(fault detection and isolation,FDI)技术的控制方法和基于自适应技术的控制方法[126-128]。前者由FDI子系统精确及时给出故障信息,进而进行控制器重构,从而构成有效的容错控制策略,但FDI易受到干扰、不确定性等因素的影响而误诊,导致系统的破坏;自适应控制方法利用自适应技术估计故障信号,控制增益响应估计信号进行实时变化,进而实现容错控制[126, 129]。
3 垂直起降运载器发展趋势
3.1 完全重复使用
由于运载器二子级再入垂直回收在经济性和技术上存在挑战,目前以Falcon 9/Heavy和New Glenn为代表的垂直起降运载器仅(计划)开展了一子级的可重复使用。Falcon 9/Heavy一子级使用的Merlin-1D系列液氧煤油发动机在使用后存在积碳问题,发动机寿命有限,在有限次重复使用后需更换发动机,增加了使用成本。因此,垂直起降运载器将进一步提高发动机与箭体、箭上设备的维护周期和寿命,运载器各子级均可控垂直回收并快速复用,即更高意义上的完全可重复使用。
3.2 单级入轨
受限于当前的科技水平,目前的垂直起降运载器未能实现单级入轨,但单级入轨始终是运载器的发展目标。单级入轨垂直起降运载器系统更为简单,所需发动机和箭上设备更少,仅需回收单一箭体即可实现完全回收,显著降低了检修和维护难度,重复使用后能进一步降低成本。
3.3 智能化
随着信息技术的进一步发展,新一代信息技术将与航天技术进行深度融合,垂直起降运载器将朝着智能化方向发展。通过智能全箭健康检测系统、智能飞行控制和智能飞行性能评估等,将进一步降低维护和使用成本,达到故障条件下的自主任务重构从而提高系统安全性,实现飞行过程中约束条件的最优性、飞行轨迹的最优性、控制系统作动量的最佳匹配性和飞行性能的综合最优性。
4 结束语
Falcon 9等运载器的成功回收并复用证明了垂直起降运载器在技术上的可行性与在成本上的优势,将可重复使用运载器的研究推向了新的阶段。本文梳理了垂直起降运载器的发展历程和现状,并针对垂直起降运载器的任务特点分析了其关键技术与解决途径,最后总结了垂直起降运载器的发展趋势,可为我国垂直起降运载器的研究和发展提供一定的参考。
[1] 王振国, 罗世彬, 吴建军. 可重复使用运载器研究进展[M]. 长沙: 国防科技大学出版社, 2004.
[2] 徐大富, 张哲, 吴克, 等. 垂直起降重复使用运载火箭发展趋势与关键技术研究进展[J]. 科学通报, 2016, 61(32): 3453-3463.
[3] 胡冬生, 郑杰, 吴胜宝. “新格伦”火箭简析及其与“猎鹰重型”火箭的对比[J]. 国际太空, 2017(6): 43-48.
[4] 高朝辉, 张普卓, 刘宇, 等. 垂直返回重复使用运载火箭技术分析[J]. 宇航学报, 2016, 37(2): 145-152.
[5] Hudson G C. History of the Phoenix VTOL SSTO and recent developments in single-stage launch systems[J]. Proceedings of 5thISCOPS, AAS, 1991, 77: 329-351.
[6] Bono P. ROMBUS-an integrated systems concept for a reusable orbital module (booster & utility shuttle)[R]. Douglas Engineering Paper, NO. 1552, 1963.
[7] Bennett F V. Apollo experience report: mission planning for lunar module descent and ascent[R]. NASA Technical Report, NASA TN D-6846, 1972.
[8] Cox K L. Design development of the apollo lunar module[C]. NASA, Washington Fourth Inter-Center Control Systems Conference, 1978.
[9] Copper J A. Single stage rocket concept selection and design[C]. AlAA Space Programs and Tech-nologies Conference, Huntsville, Alabama, 1992.
[10] Weegar R K. SSTO propulsion design[C]. AlAA Space Programs and Technologies Conference, Huntsville, Alabama, 1992.
[11] 祁锋. 火箭型单级入轨(SSTO)的初步分析[J]. 推进技术, 1996, 17(4): 61-68.
[12] Freeman D C, Talay T A, Austin R E. Single-stage-to-orbit-meeting the challenge[J]. Acta Astronautica, 1996, 38(4-8): 323-331.
[13] Freeman D C, Talay T A, Austin R E. Reusable launch vehicle technology program[J]. Acta Astronautica, 1997, 41(11): 777-790.
[14] Inatani Y, Naruo Y, Yonemoto K. A concept and flight testing of fully reusable rocket vehicle[C]. AIAA 9thInternational Space Planes and Hypersonic Systems and Technologies Conference, Norfolk, Virginia, 1999.
[15] Inatani Y, Naruo Y, Yonemoto K. Concept and preliminary flight testing of a fully reusable rocket vehicle[J]. Journal of Spacecraft and Rockets, 2001, 38(1): 36-42.
[16] Naruo Y, Tokudome S-I, Ishii M, et al. Design and operational aspect of LOX/LH2 propulsion system of reusable vehicle testing (RVT)[C]. AIAA 10thInternational Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 2001.
[17] Ogawa H, Nonaka S, Inatani Y. A concept and its aerodynamic design of a sub-orbital reusable rocket[C]. 34thAIAA Fluid Dynamics Conference and Exhibit, Portland, Oregon, 2004.
[18] Himeno T, Watanabe T, Nonaka S, et al. Sloshing prediction in the propellant tanks of VTVL rocket vehicle[C]. 41stAIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit, Tucson, Arizona, 2005.
[19] Masten’s reusable launch vehicles & landers[EB/OL]. Masten Space Systems official website; http://masten.aero/vehicles-2/, 2017-12-31.
[20] Dreyer L. Latest developments on SpaceX’s Falcon 1 and Falcon 9 launch vehicles and Dragon spacecraft[C]. 2009 IEEE Aerospace Conference, Big Sky, Montana, 2009.
[21] 张雪松. 艾伦·马斯克的终极梦想--可重复使用运载火箭[J]. 太空探索, 2014(7): 28-31.
[22] Launch manifest[EB/OL]. http://www. spacex. com/missions, 2017-12-31.
[23] SpaceX news[EB/OL]. https://www. nasaspaceflight. com/news/spacex/, 2017-12-31.
[24] 张浩. 太空探索技术公司放弃“龙”飞船有动力着陆方案[J]. 中国航天, 2017(9): 50-51.
[25] SpaceX. Making Life Multiplanetary[EB/OL]. 2017.
[26] 罗亚中, 唐国金, 梁彦刚, 等. GTO发射轨道的两级分解全局优化设计策略[J]. 中国空间科学技术, 2004(4): 38-48.
[27] 黄荣, 崔乃刚, 韦常柱, 等. 基于RRT-GPM两阶策略的导弹编队协同突防最优轨迹快速设计[J]. 中国惯性技术学报, 2015, 23(3): 356-362.
[28] Liu X, Lu P, Pan B. Survey of convex optimization for aerospace applications[J]. Astrodynamics, 2017, 1(1): 23-40.
[29] Sagliano M, Theil S, Bergsma M, et al. On the radau pseudospectral method: theoretical and implementation advances[J]. Ceas Space Journal, 2017, 9(3): 313-331.
[30] 何炬. 国外天文导航技术发展综述[J]. 舰船科学技术, 2005(5): 91-96.
[31] 詹银虎. 测日天文导航理论及技术研究[J]. 测绘学报, 2017, 46(2): 267.
[32] 李群生, 赵剡, 鲁浩, 等. 捷联惯导/天文导航/合成孔径雷达组合导航系统[J]. 仪器仪表学报, 2017(11): 2667-2674.
[33] 薛喜平, 张洪波, 孔德庆. 深空探测天文自主导航技术综述[J]. 天文研究与技术, 2017, 14(3): 382-391.
[34] Zhao S, Lin F, Peng K, et al. Vision-aided estimation of attitude, velocity, and inertial measurement bias for UAV stabilization[J]. Journal of Intelligent & Robotic Systems, 2016, 81(3-4): 531.
[35] Li J, Cui H, Tian Y. Nonlinearity analysis of measurement model for vision-based optical navigation system[J]. Acta Astronautica, 2015, 107: 70-78.
[36] 姜肖楠. 月球探测器软着陆视觉导航方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
[37] 张洪华, 关轶峰, 黄翔宇, 等. 嫦娥三号着陆器动力下降的制导导航与控制[J]. 中国科学:技术科学, 2014, 44(4): 377-384.
[38] 赵一鸣, 李艳华, 商雅楠, 等. 激光雷达的应用及发展趋势[J]. 遥测遥控, 2014, 35(5): 4-22.
[39] 汪备. 基于激光雷达的行星软着陆自主障碍检测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
[40] 刘琳. 北斗/GPS双模差分定位技术的研究及实现[D]. 北京: 北京交通大学, 2013.
[41] 柴进柱, 黄永军. 北斗沿海差分导航与精密定位服务系统[J]. 海洋测绘, 2016, 36(3): 41-43.
[42] 刘斌. 重复使用运载器先进导航技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[43] 黄盘兴. 运载器大气层内上升段轨迹快速优化方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[44] Chandler D C, Smith I E. Development of the iterative guidance mode with its application to various vehicles and missions[J]. Journal of Spacecraft and Rockets, 1967, 4(7): 898-903.
[45] 韩祝斋. 用于大型运载火箭的迭代制导方法[J]. 宇航学报, 1983(1): 9-21.
[46] 陈新民, 余梦伦. 迭代制导在运载火箭上的应用研究[J]. 宇航学报, 2003, 24(5): 484-489.
[47] 茹家欣. 液体运载火箭的一种迭代制导方法[J]. 中国科学(E辑:技术科学), 2009, 39(4): 696-706.
[48] 王大轶, 李铁寿, 严辉, 等. 月球引力转弯软着陆的制导控制研究[J]. 中国空间科学技术, 2000 (5): 17-23.
[49] Jungmann J A. The exact analytic solution of the lunar landing problem (lunar landing problem, determining position, velocity and acceleration as functions of time from ignition to shutdown)[C]. American Astronautical society, Space flight mechanics specialist, Denver, Colorado, USA, 1966.
[50] Feng T Y, Wasynczuk C A. Terminal guidance for soft and accurate lunar landing for unmanned spa-cecraft[J]. Journal of Spacecraft, 1968, 5: 644-648.
[51] Cheng R K, Conrad D A, Meredith C M. Design considerations for surveyor guidance[J]. Journal of Spacecraft and Rockets, 1966, 3(11): 1569-1576.
[52] Mcinnes C R. Nonlinear transformation methods for gravity-turn descent[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(1): 247-248.
[53] Mcinnes C R. Direct adaptive control for gravity-turn descent[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(2): 373-375.
[54] Chomel C T, Bishop R H. Analytical lunar descent guidance algorithm[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(3): 915-926.
[55] Sostaric R R, Rea J R. Powered descent guidance methods for the moon and Mars[C]. AIAA Guidance, Navigation, and Control Conference and Exh-ibit, San Francisco, California, USA, 2005.
[56] 蔡艳芳. 月球探测器软着陆制导控制方法研究[D]. 西安: 西北工业大学, 2006.
[57] 朱建丰, 徐世杰. 月球重力转弯软着陆的模糊变结构控制[J]. 北京航空航天大学学报, 2007, 33(5): 539-543.
[58] Hou M Z, Duan G R. Robust adaptive dynamic surface control of uncertain nonlinear systems[J]. International Journal of Control, Automation and Systems, 2011, 9(1): 161-168.
[59] 刘晓东, 黄万伟, 禹春梅. 含扩张状态观测器的高超声速飞行器动态面姿态控制[J]. 宇航学报, 2015, 36(8): 916-922.
[60] 宋晨, 周军, 郭建国, 等. 高超声速飞行器基于路径跟踪的制导方法[J]. 宇航学报, 2016, 37(4): 435-441.
[61] 雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙: 国防科学技术大学, 2008.
[62] 杜昕. 探月返回跳跃式再入轨迹规划与制导[D]. 长沙: 国防科学技术大学, 2015.
[63] 黄荣. 助推—补能滑翔飞行器参数/轨迹优化与在线制导方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
[64] Kim B S, Lee J G, Han H S. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288.
[65] Ratnoo A, Ghose D. Impact angle constrained interception of stationary targets[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1817-1822.
[66] Lee Y I, Ryoo C K, Kim E. Optimal guidance with constraints on impact angle and terminal acceleration[C]. AIAA Guidance, Navigation, and Control Conference, Austin, Texas, USA, 2003.
[67] Kumar S R, Rao S, Ghose D. Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1114-1130.
[68] 蔡洪, 胡正东, 曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报, 2010, 31(2): 315-323.
[69] Klumpp A R. Apollo lunar descent guidance[J]. Automatica, 1974, 10: 133-146.
[70] Cherry G W. A general, explicit, optimizing guidance law for rocket-propelled spaceflight[C]. Astrodynamics Guidance and Control Conference, Los Angeles, California, USA, 1964.
[71] D’Souza C. An optimal guidance law for planetary landing[C]. AIAA Guidance, Navigation, and Control Conference, New Orleans, Louisana, USA, 1997.
[74] Liu X, Lu P. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 750-765.
[75] Liu X, Shen Z, Lu P. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 227-241.
[76] Wang Z, Grant M J. Constrained trajectory optimization for planetary entry via sequential convex programming[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2603-2615.
[77] Wang J, Cui N. A pseudospectral-convex opti-mization algorithm for rocket landing guidance[C]. 2018 AIAA Guidance Navigation and Control Conference, Kissimmee, Florida, USA, 2018.
[78] Scharf D P, Akmee B, Dueri D, et al. Implementation and experimental demonstration of onboard powered-descent guidance[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(2): 213-229.
[79] Bauer H F. Stability boundaries of liquid-propelled elastic space vehicles with sloshing[J]. Journal of Spacecraft and Rockets, 1966, 3(2):
[80] Unruh J F, Kana D D, Dodge F T, et al. Digital data-analysis techniques for extraction of slosh model parameters[J]. Journal of Spacecraft and Rockets, 1986, 23(2): 171-177.
[81] Kana D D. A model for nonlinear rotary slosh in propellant tanks[J]. Journal of Spacecraft and Rockets, 1987, 24(2): 169-177.
[82] 董锴. 航天器推进剂晃动的动力学建模与抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
[83] Berry R L, Tegart J R, Experimental study of transient liquid motion in orbiting spacecraft[R]. NASA Technical Report, NASA-CR-144213, 1975.
[84] 黄华, 杨雷, 张熇, 等. 航天器贮箱大幅液体晃动三维质心面等效模型研究[J]. 宇航学报, 2010, 31(01): 55-59.
[85] Zhou Z C, Huang H. Constraint surface model for large amplitude sloshing of the spacecraft with multiple tanks[J]. Acta Astronautica, 2015, 111: 222-229.
[86] Vreeburg J P B. Dynamics and control of a spacecraft with a moving pulsating ball in a spherical cavity[J]. Acta Astronautica, 1997, 40(2-8): 257-274.
[87] Vreeburg J P B. Spacecraft maneuvers and slosh control[J]. IEEE Control Systems Magazine, 2005, 25(3): 12-16.
[88] 邓明乐, 岳宝增, 黄华. 液体大幅晃动类等效力学模型研究[J]. 宇航学报, 2016, 37(6): 631-638.
[89] Deng M L, Yue B Z. Attitude dynamics and control of liquid filled spacecraft with large amplitude fuel slosh[J]. Journal of Mechanics, 2016, 33(1): 125-136.
[90] Deng M L, Yue B Z. Attitude dynamics and control of spacecraft with multiple liquid propellant tanks[J]. Journal of Aerospace Engineering, 2016, 29(6): 04016042.
[91] Deng M L, Yue B Z. Nonlinear model and attitude dynamics of flexible spacecraft with large amplitude slosh[J]. Acta Astronautica, 2017, 133: 111-120.
[92] Vreeburg J P B. Measured states of sloshsat FLEVO[C]. Proceedings of the 56thInternational Astronautical Congress International Astronautical Federa-tion, 2005.
[93] Vreeburg J P B. Acceleration measurements on sloshsat FLEVO for liquid force and location determination[C]. 4thESA International Conference on Spacecraft Guidance, Navigation and Control Systems and Tutorial on Modern and Robust Control, Noordwijk, the Netherlands, 1999.
[94] Chen W H, Yang J, Guo L, et al. Disturbance-observer-based control and related methods-an overview[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083-1095.
[95] Khalil H K, Praly L. High-gain observers in nonlinear feedback control[J]. International Journal of Robust and Nonlinear Control, 2014, 24(6): 993-1015.
[96] Jung J, Huh K, Fathy H K, et al. Optimal robust adaptive observer design for a class of nonlinear systems via an H-infinity approach[C]. Proceedings of the 2006 American Control Conference, Minneapolis, Minnesota, USA, 2006.
[97] Guo B Z, Zhao Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430.
[98] Zhao Z L, Guo B Z. A nonlinear extended state observer based on fractional power functions[J]. Automatica, 2017, 81: 286-296.
[99] Levant A. Higher-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9-10): 924-941.
[100] Cruz-Zavala E, Moreno J A, Fridman L M. Uniform robust exact differentiator[J]. IEEE Transactions on Automatic Control, 2011, 56(11): 2727-2733.
[101] Angulo M T, Moreno J A, Fridman L. Robust exact uniformly convergent arbitrary order differentiator[J]. Automatica, 2013, 49(8): 2489-2495.
[102] Basin M, Yu P, Shtessel Y. Finite- and fixed-time differentiators utilising HOSM techniques[J]. IET Control Theory and Applications, 2017, 11(8): 1144-1152.
[103] 王子瑞. 大推力运载火箭姿态控制的研究[D]. 武汉: 华中科技大学, 2013.
[104] 王晔, 程昊宇. 运载火箭姿态的自抗扰控制器设计[J]. 弹箭与制导学报, 2015, 35(4): 11-14.
[105] Zhang L, Wu R, Wei C Z, et al. Quaternion-based reusable launch vehicle composite attitude control via active disturbance rejection control and sliding mode approach[C]. 21stAIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 2017.
[106] Shtessel Y, Tournes C, Krupp D. Reusable launch vehicle control in sliding modes[C]. AIAA Guidance, Navigation, and Control Conference, New Orleans, Louisana, USA, 1997.
[107] Shtessel Y, Mcduffie J, Jackson M, et al. Sliding mode control of the X-33 vehicle in launch and re-entry modes[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Boston, Massachusetts, USA, 1998.
[108] Shtessel Y B, Hall C, Baev S, et al. Flexible modes control using sliding mode observers: application to Ares I[C]. AIAA Guidance, Navigation, and Control Conference, Toronto, Ontario, Canada, 2010.
[109] Su R, Zong Q, Tian B L, et al. Comprehensive design of disturbance observer and non-singular terminal sliding mode control for reusable launch vehicles[J]. IET Control Theory and Applications, 2015, 9(12): 1821-1830.
[110] 孙慧杰. 火箭起飞段姿态系统的滑模变结构控制[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[111] Xia Y, Fu M. Compound control methodology for flight vehicles[M]. Berlin: Springer, 2013.
[112] 晁涛. 飞行器复合控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.
[113] 许江涛. 可重复使用助推飞行器姿态控制和控制分配研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
[114] Bordignon K A. Constrained control allocation for systems with redundant control effectors[D]. Blacksburg: Virginia Tech, 1996.
[115] Durham W C. Constrained control allocation[J]. Journal of Guidance, Control, and Dynamics, 1993, 16(4): 717-725.
[116] Teel A, Buffington J, Teel A, et al. Anti-windup for an F-16’s daisy chain control allocator[C]. Guidance, Navigation, and Control Conference, 1997.
[117] Bodson M. Evaluation of optimization methods for control allocation[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(4): 703-711.
[118] Bolender M A, Doman D B. Nonlinear control allocation using piecewise linear functions[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 1017-1027.
[119] 曹宗涛, 马瑞平, 张明廉. 一种飞行控制中控制分配的解决方案[J]. 飞行力学, 2006(1): 17-21.
[120] Johansen T A, Fossen T I, Berge S P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J]. IEEE Transactions on Control Systems Technology, 2004, 12(1): 211-216.
[121] 周锐, 杨晓东, 王军. 具有异构多操纵机构的飞行器复合控制技术[J]. 宇航学报, 2008(4): 1297-1301.
[122] Fan Y, Zhu J, Sun Z. Fuzzy logic based constrained control allocation for an advanced fighter[C]. Computational Intelligence for Modelling, Control and Automation, 2006 and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, International Conference on. IEEE, 2006: 200.
[123] 马建军, 李文强, 李鹏, 等. 飞行器控制分配技术研究现状与展望[J]. 飞行力学, 2009, 27(3): 1-5.
[124] 高志峰. 复杂系统的容错控制技术及其在近空间飞行器中的应用研究[D]. 南京: 南京航空航天大学, 2011.
[125] 张亮, 黄盘兴, 徐大富, 等. 垂直起降火箭垂直返回段自适应容错控制算法[J]. 战术导弹技术, 2015(2): 63-69.
[126] 金小峥, 原忠虎, 李彦平. 主动容错控制理论——自适应方法[M]. 北京: 电子工业出版社, 2014.
[127] Jiang J, Yu X. Fault-tolerant control systems: A comparative study between active and passive approaches[J]. Annual Reviews in Control, 2012, 36(1): 60-72.
[128] Zhang Y, Jiang J. Bibliographical review on reconfigurable fault-tolerant control systems[J]. Annual reviews in Control, 2008, 32(2): 229-252.
[129] 王福利, 张颖伟. 容错控制[M]. 沈阳: 东北大学出版社, 2003.
