具有飞跨电容辅助桥臂的五电平高压并网逆变器
2018-04-16魏米兰曾翔君龚德林
魏米兰, 曾翔君, 汪 航, 谢 静, 龚德林
(西安交通大学电气工程学院, 陕西省西安市 710049)
0 引言
目前,在超大功率(5 MW以上)直驱风能变换系统(WECS)中,中高压多电平或多模块全功率变换器由于可以提高输出电压、降低电流、实现无升压变压器并网等特点而受到越来越多的重视[1-2]。对于多模块变换器,模块化多电平换流器(MMC)和级联H桥的电压源换流器(CHB-VSC)拓扑被广泛的研究。MMC的每相桥臂均由多个子模块级联而成,这使得其具有拓展性强、设计灵活以及易于投入工程实际的优点。除此之外,MMC输出电平数随子模块数的增加而增加,在多电平输出情况下,具有输出电压谐波含量较低的优点。虽然MMC及其衍生的拓扑具有上述优点,但MMC在运行过程中由于电容电压存在交流脉动以及不均衡的情况,会产生相间环流,该环流会引起负序分量,造成相电流的不平衡。为了消除环流的影响并保持相间能量的平衡,需要引入复杂的环流抑制方法,比如文献[3]提出的改进载波移相调制策略。同时每个子模块都需要一个直流电容,并且为了平抑低频电压的脉动,电容的容量选择比较大,这将导致变流器的体积和成本比较高[4-5]。另外,MMC的每个桥臂都需要两个滤波电感,且由于有直流电流流过,存在直流偏磁的问题。
CHB-VSC是通过基本的H桥单元级联来实现高电压,但在功率传输过程中,每个单元需要一个变压器或多绕组发电机来提供独立直流电源,直流电源的获得比较困难,而且该种拓扑不易实现四象限运行,使系统的构成和控制方法比较复杂[6-7]。
相比之下,中点钳位(NPC)多电平变换器是如今广泛应用于中高压变换系统的单变换器[8]。它既不需要多个独立的直流电源,也不需要数量众多的电容器,只需要小容量电容器平抑直流母线的高频纹波。同时与MMC和CHB-VSC相比,还具有开关控制易于实现以及保护电路简单等优点,从而能够降低成本和控制复杂性。目前得到广泛应用的多电平拓扑是三电平中点钳位(3L-NPC)变换器,但3L-NPC变换器具有较低的输出电压,需要一个升压变压器来连接电网[9-10]。相比之下,五电平中点钳位(5L-NPC)变换器可以产生比3L-NPC变换器更高的电压和功率,还可以实现更高的效率。例如利用6 500 V等级的绝缘栅双极型晶体管(IGBT)器件可实现10 kV交流电压输出等级,因此可直接与10 kV电网并联,而不需要升压变压器。但是其直流侧存在中点不平衡问题,使得变换器性能下降甚至不能正常工作。为了解决该问题,国内外学者提出了许多解决方案,主要分为两种:修改调制策略和添加辅助电路。文献[11-18]给出修改调制策略的方法,一种是在支持向量机(SVM)矢量调制中不使用与电容中点相关的电压矢量,从而避免了直流电流流经电容中点造成的电压失衡,但采用这种调制策略也就意味着一个五电平逆变器电压输出将退化成一个三电平输出,这不仅会增加谐波,同时也会导致每个周期的开关动作次数增加,从而增加了开关损耗。另一种调制策略则是调整冗余矢量对占空比的控制策略,这种策略不会引起损耗和谐波的明显变化,但是它的控制能力只能局限在有限的功率因数和调制度下,在高功率因数与高调制度条件下无法使电容中点电压保持平衡。国内外利用添加辅助电路来实现中点电压平衡的方法有很多,文献[19-22]中提出的是基于电感的辅助电路。为了维持中点电压的平衡,由逆变器注入中点的失衡电流必须全部流经直流电抗器,从而存在电感的体积和功率损耗都很大的问题。
本文提出了一种基于自平衡飞跨电容辅助桥臂的新型5L-NPC逆变器拓扑,利用辅助桥臂的中点替换直流母线电容的中点,并通过飞跨电容技术和简单的控制来实现中点的自平衡,并且不使用电感,从而可以实现更高的效率。本文将对这种新型拓扑的结构、工作原理和控制方法进行研究。
1 拓扑结构
图1展示了所提5L-NPC逆变器的拓扑,它由以下三部分构成:常规5L-NPC开关拓扑、飞跨电容辅助桥臂和LCL滤波器。辅助桥臂由上下两个三电平飞跨电容(3L-FC)桥臂(即Cf1和Cf2)以及一个跨接于中点A与B之间的飞跨电容Cf3(串联一个电阻Rf)构成。O点为直流母线电容(Cdc1和Cdc2)的中点,而常规5L-NPC的直流电容中点A和B被Cf1和Cf2飞跨电容桥臂的中点代替。Cf1和Cf2的引入是为了实现A和B点的电压平衡,而Cf3的引入是为了实现O点电压的平衡。
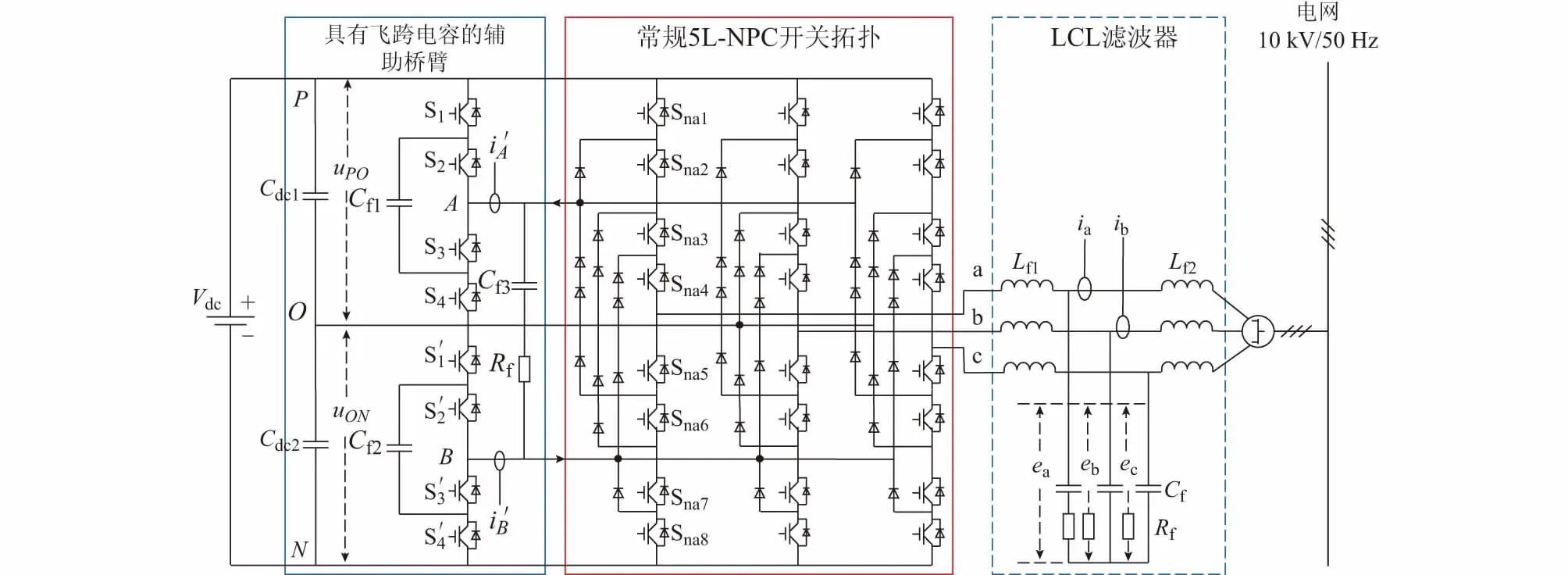
图1 具有辅助桥臂的5L-NPC逆变器拓扑Fig.1 5L-NPC inverter topology with auxiliary bridge arm
对于额定输出为10 MW/10 kV的逆变器系统,若直流母线电压等于16 kV,则本文所提5L-NPC逆变器与MMC两种方案使用的有源和无源器件数目以及硅成本的对比如附录A表A1所示(采用6 500 V/750 A商用IGBT和快速恢复二极管(FRD)芯片作为对比依据)。
附录A表A1中IGBT和FRD的成本只考虑管芯的成本,而不考虑封装成本等,根据IGBT模块封装厂提供的数据,同样等级的FRD的成本大致为IGBT的1/3左右。由附录A表A1可知,所提5L-NPC逆变器使用更少的IGBT,虽然使用的FRD较多,但是总硅成本仍比MMC少。另外,所提5L-NPC使用的直流电容和无源元件较MMC要少很多,这使得其具有更低的体积和成本。同时,所提5L-NPC的控制方法相比MMC更简单,不需要复杂的环流控制,因此5L-NPC相比MMC具有很明显的优势。
2 中点平衡控制
2.1 A和B点平衡控制策略
常规5L-NPC逆变器具有固有的中点电压不平衡问题,主要包括以下两个方面:一个是中点A和B的电压不平衡;另一个是中点O的电压不平衡。其中A和B的电压不平衡是因为当逆变器在高调制度和高功率因数条件下稳定运行时,逆变器将产生直流电流注入中点A和B,进而导致其电压失衡。对此,本文提出添加两个串联的3L-FC辅助桥臂,用桥臂中点代替电容中点的控制方案。为证明其有效性,一个简化的等效电路模型如附录A图A1所示。
附录A图A1中,由于本文采用的开关频率为2.5 kHz,在这个频率下相电流可以作为恒流源,因此此处将相电流等效成恒流源(ia,ib和ic),恒流源电流经5L-NPC开关电路转变为P,A,O,B,N间流动的直流电流。以A点为例,由逆变器流至A点的直流电流iA可表示为:
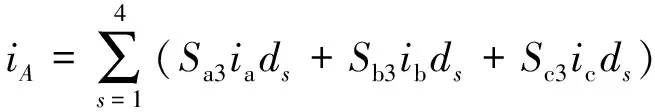
(1)
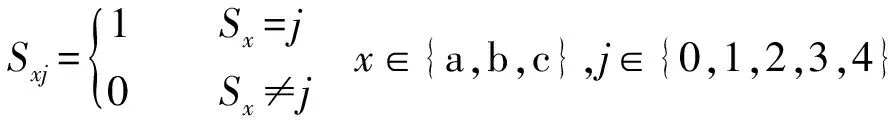
(2)
式中:Sxj为5L-NPC逆变器每相桥臂的5种开关状态(分别用0,1,2,3,4表示)所对应的开关函数;ds为该开关状态所对应的占空比。
以a相为例,当选择不同的开关函数Sa0至Sa4时,恒流源ia分别与直流母线的P,A,O,B和N接通。式(1)中Sxj和ds取决于逆变器SVM调制器的调制度m和功率因数角φ。当采用文献[23]给出的SVM调制方法时,可以画出不同功率因数角φ与调制度m下中点电流iA的平均值|IA|的归一化值,即|IA/Ia_ph|,其中Ia_ph为a相电流的峰值,如附录A图A2所示。流经B点的直流电流与A点大小相同,方向相反。
由附录A图A2可看出,当功率因数接近0时,几乎没有直流电流流入A和B点,但当功率因数为1时,逆变器可产生高于50%相电流峰值的直流电流注入中点A和B,从而引起A和B点电压不平衡。对此,本文采用两个串联的3L-FC辅助桥臂提供电流通路来抵消流经电流对中点电压平衡的影响。
3L-FC桥臂有4种开关状态,但只有两种被使用,以上桥臂为例,分别是O1(S1开,S2关,S3开,S4关)和O2(S1关,S2开,S3关,S4开)。则上下桥臂开关状态有4种组合,其中对O点有平衡作用的状态组合只有O1-O1与O2-O2,理想状态下其占空比均近似为50%,因此此处选取这两种主要的开关状态O1-O1与O2-O2对A点电压平衡控制进行分析,这两种开关状态下5L-NPC逆变器简化电路图如附录A图A3所示(为维持O点平衡引入Cf3与串联电阻Rf)。其中,来自5L-NPC的中点电流iA和iB既含直流分量又有交流脉动分量,直流分量被用于Cf1和Cf2的平衡控制,由于交流分量只会导致电压脉动而不会引起Cf1和Cf2的电压失衡,因此在分析Cf1和Cf2的平衡控制时可以用直流恒流源来代替iA和iB。
A点电压平衡控制(B点类似)将根据附录A图A3给出的两种状态下辅助桥臂等效电路进行分析。为简化分析,假定此时O点电压是平衡的,即VPO=VON=Vdc/2。根据附录A图A3所给等效电路,若飞跨电容Cf1两端电压ucf1被控为Vdc/4,则在开关状态为O1-O1时,VAO=VPO-ucf1=Vdc/4,而在开关状态为O2-O2时,VAO=ucf1=Vdc/4,即在任意时刻VAO=VPO/2,A点电压平衡。同理,若飞跨电容Cf2两端电压ucf2被控制为Vdc/4,则B点电压平衡,从而实现了中点A和B的平衡。
若不添加飞跨电容Cf3,则恒流源iA的电流全部流至飞跨电容Cf1,使得在O1-O1状态下,Cf1一直放电,在O2-O2状态下,Cf1一直被充电。这样就能通过调节O1-O1和O2-O2状态占空比(dO1与dO2)来控制A点电压平衡,并且在平衡时dO1=dO2=50%。
添加飞跨电容Cf3后,根据附录A图A3(a)中O1-O1状态下的等效电路,可看出iA的部分电流分流流入了Cf3,此时流经Cf1的电流为:
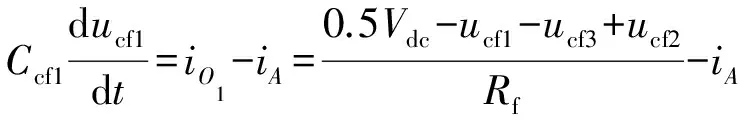
(3)
由式(3)可知,开关状态为O1-O1时,飞跨电容Cf1的充放电状态不仅取决于iA的大小,还与iO1有关。iO1决定于飞跨电容Cf1,Cf2与Cf3的瞬时电压值和串联电阻Rf的大小。当iO1
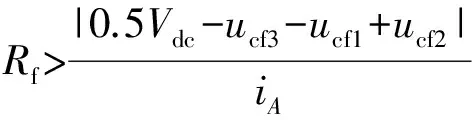
(4)
同理,根据附录A图A3(b)给出的在O2-O2状态下添加Cf3辅助桥臂后的等效电路,此时流经Cf1电流为:
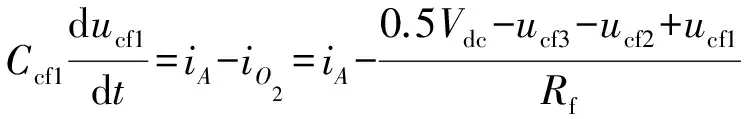
(5)
由式(5)可知,在O2-O2状态下,电容Cf1充放电同样与Cf1,Cf2与Cf3瞬时电压值和电阻Rf有关。通过选取合适Rf值,使iA电流值大于|iO2|时,能确保在O2-O2状态下电容Cf1一直被充电。此时,串联电阻Rf的阻值应满足:
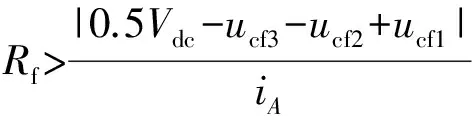
(6)
最终,所选取的电阻Rf的阻值需同时满足式(4)与式(6),式中的分母电流项采用iA的直流分量,分子中的瞬时电压差则由iA的交流分量在Cf1和Cf2上引起的电压差来估计。这样就能通过调节O1-O1和O2-O2状态占空比使飞跨电容Cf1稳定在Vdc/4。当Rf值足够大,则iA将远大于|iO1|,分流至Cf3电流几乎可忽略,此时两种状态占空比均接近50%。由于上下桥臂可以独立控制,相互隔离,可采用类似的原则控制下桥臂去平衡Cf2的电压,使两端电压ucf2稳定在Vdc/4。
2.2 O点平衡控制策略
在理想情况下,由逆变器产生的流入O点的直流电流为零,因此O点电压是平衡的。但在实际情况中,由于死区、谐波和不均匀的器件电压降等非理想因数,O点存在直流电压漂移现象,除此之外,由两个3L-FC辅助桥臂引起的O点的直流漂移电流也不能被忽略。
为解决O点的直流漂移问题,在辅助电路中跨接于A,B点之间的飞跨电容Cf3可实现O点电压的自平衡。为说明Cf3对O点的平衡原理,一个简化的5L-NPC逆变器模型如附录B图B1所示。图中,飞跨电容器Cf1和Cf2被两个Vdc/4直流电压源代替,由于从5L-NPC流至A和B点的恒定电流iA,iB对O点电压平衡没有直接的影响,此处则将两恒流源做断开处理(图中用红色叉号表示)。除此之外,考虑到理想开关模型不能反映O点的实际直流漂移现象,在附录B图B1的模型中采用向O点注入具有5%峰值相电流幅度的恒定直流电流Idrift来模拟漂移电流。
根据附录B图B1的模型,在O1-O1和O2-O2状态下的辅助桥臂简化电路如图2(a)和(b)所示。
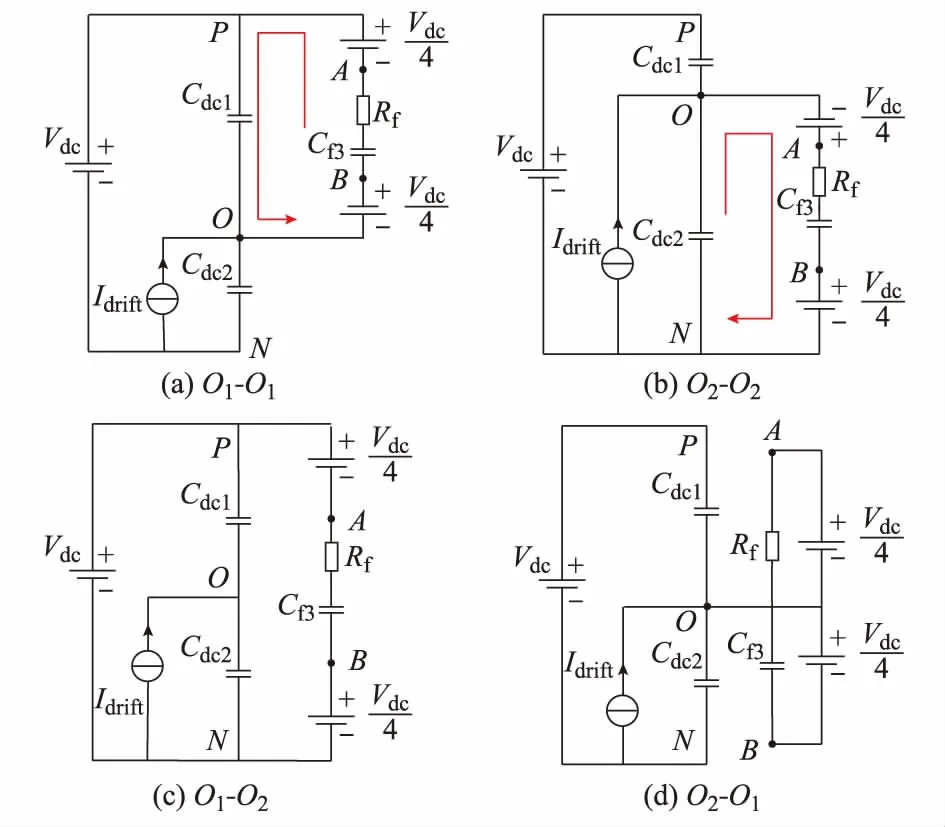
图2 4种开关组合状态下辅助桥臂简化电路图Fig.2 Simplified circuit diagrams of auxiliary bridge arm under four switch combination states
由图2可知,在O点电压平衡情况下,Cf3的稳态电压为Vdc/2。但是在漂移电流的作用下,Cdc2会被充上过量的电荷使它的电压升高,同时Cdc1上的电压下降。根据图2(b)可知,在O2-O2状态下Cdc2上的过量电荷将向Cf3释放,然后在图2(a)给出的O1-O1状态下补充回Cdc1上,进而对O点失衡起到抑制的作用。
除此之外,另外两种开关状态(O1-O1和O2-O1)下辅助桥臂简化电路如图2(c)和(d)所示。可以看出,O1-O2和O2-O1开关状态下没有可以补偿Idrift的电流流入O点,因此O1-O2和O2-O1状态对O点电压没有影响,但它所构成的电流回路可以将Cf3两端的电压钳位至Vdc/2。与飞跨电容Cf3串联的电阻Rf是为了限制开关瞬间冲击电流,以防止器件损坏,但是过大的Rf会抑制Cf3向Cdc1和Cdc2的充放电电流,对O点的电压平衡是不利的。
因此在上下桥臂的4种开关状态的组合中,只有O1-O1和O2-O2状态对O点有平衡作用。从而在利用飞跨电容Cf3对O点进行控制时,应尽量采用O1-O1和O2-O2状态。由前文2.1节的讨论可知,在控制电流iA和iB很大的情况下,上桥臂和下桥臂的O1和O2两种开关状态占空比各占50%,因此上下桥臂O1-O1和O2-O2组合状态占空比也均接近50%。这对于O点平衡是非常有利的。如果仅有图2(a)和(b)两种状态,可推导出O点的电压偏差与电阻Rf的关系为:
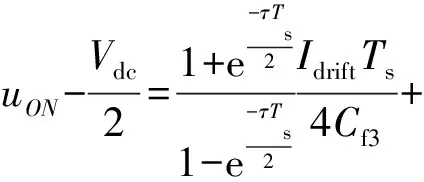
(7)
式中:τ=(2Cdc+Cf3)/(2CdcRfCf3);Ts为开关周期。
由式(7)可知,O点产生的电压偏差与Rf的取值成正比。因此Rf的取值还应根据允许的电压偏差ΔUON来选择。
为维持50%的占空比,要么选择一个比较大的电阻Rf值,要么提供一个大的控制电流iA和iB。由附录A图A2可知,在高功率因数条件下,由逆变器注入中点A的电流iA高于相电流峰值的50%,此时选择较小的Rf值就可以实现O1-O1和O2-O2状态的占空比均接近50%的要求。但当功率因数接近0时,由逆变器流至A点的直流电流iA几乎为0,这将导致Cf3的分流作用明显,O1-O1和O2-O2状态的占空比小于50%,此时,Cf3对O点电压的平衡能力将减弱。为了产生一个新的平衡电流,本文对调制策略进行了修改。它的主要思想是在空间矢量脉宽调制(SVPWM)图中找到一些冗余矢量对,通过调整冗余矢量对的占空比来产生流入O点直流电流,抵消漂移电流对O点电压的影响。
附录B图B2给出了逆变器在高功率因数条件下工作时冗余矢量对控制的SVPWM图。图中扇形区域Ⅰ和Ⅱ为5L-NPC逆变器的SVPWM图的两个调制区域。其中在高调制度区域(m>0.75)给出了4个参考电压矢量V1至V4,它们由所在每个小三角形区域中的相邻矢量来合成。附录B图B2下方给出了合成电压矢量V1至V4的空间矢量选择及其排列顺序。
以电压矢量V1为例,合成V1的矢量顺序分为7段:[421]-[411]-[410]-[310]-[410]-[411]-[421],其中X点[421]和[310]是冗余矢量对。[421]包含开关状态“2”,选择此状态会使逆变器b相的电流被注入O点,即iO=ib(假设此时ib为正方向)。而[310]不包含“2”状态,从而不会产生流经O点电流。因此在一个短的开关周期内无法通过调整X点的冗余矢量对的占空比来产生流入O点的反向电流。而另外两个电压矢量V2和V3的冗余矢量对(分别为[411]和[300],[033]和[144])不包括“2”,因此对O点平衡没有影响。但在一个长的基波周期内,可以找到一个与X点相角相差180°的Y点,Y点的冗余矢量对[023]和[134]中,[134]不产生流经O点的电流,而[023]同样会使得逆变器b相电流流入O点,由于此时b相电流的极性与选择X点的时刻相反,因此iO=-ib。这样就可以通过调整X点冗余矢量[421]和Y点冗余矢量[023]的占空比来产生流经O点的可正可负的净可控电流。在一个基波周期内,假设d0为分配给冗余矢量对[421]和[023]总占空比,d1为矢量[421]占空比,d4为矢量[023]占空比。当无Idrift注入时,O点电压平衡,根据对称性,d1=d4=d0/2,流入O点的净电流iO=d1ib-d4ib=0。注入Idrift后,为平衡O点电压,d1和d4重新分配,变量α(-1≤α≤1)用于重新分配d1和d4。这样在一个基波周期内流入O点的净可控电流为:
iO=d1ib-d4ib=
(8)
由式(8)可知,通过调节控制变量α可以控制出用于抵消Idrift的直流电流iO,但其控制能力受到调制度和功率因数的影响,最大可控直流电流IOm的归一化值(即|IOm/Ia_ph|)与调制度和功率因数角关系图如附录B图B3所示。只要Idrift小于最大可控直流电流IOm,O点就可以平衡。
由附录B图B3可知,修改调制策略后,高调制度条件下功率因数为0时,利用调整冗余矢量对的占空比的方法可以产生较大直流电流入O点,进而实现O点电压的平衡。也就意味着,在低功率因数下辅助桥臂对O点电压平衡无法产生足够影响时,通过修改调制策略可以对O点电压提供足够的平衡能力。
3 控制策略
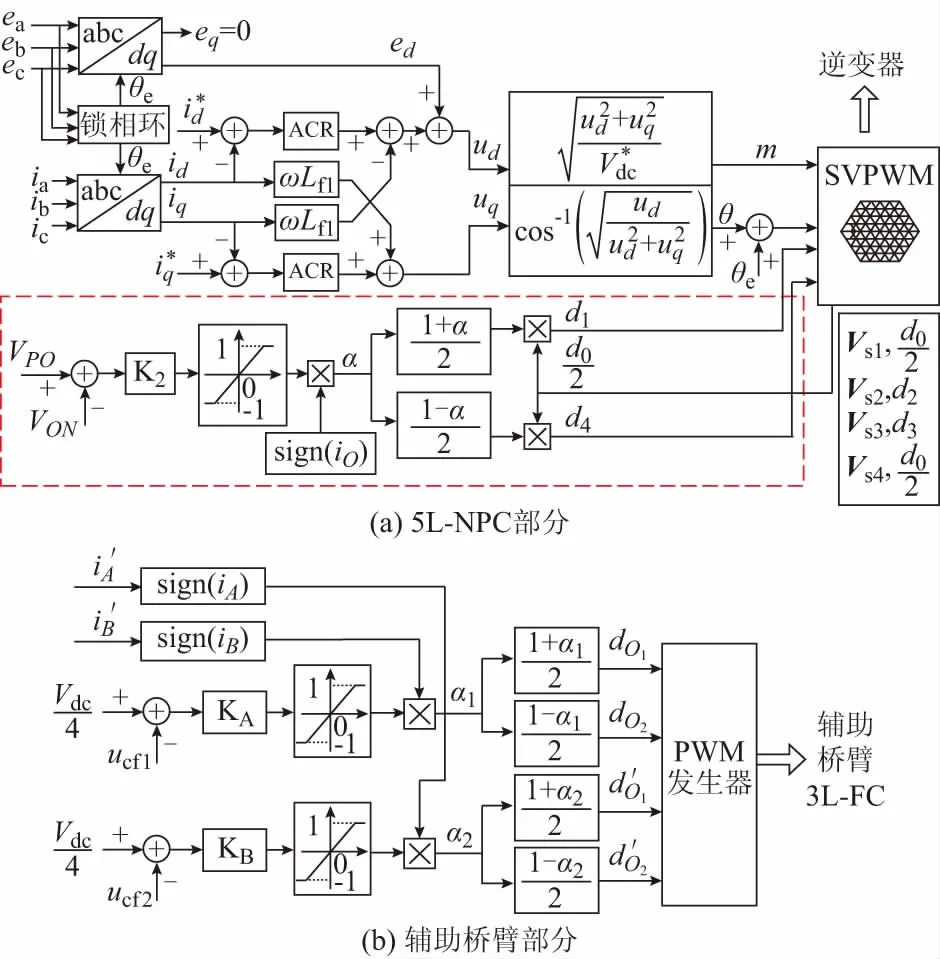
图3 逆变器的控制框图Fig.3 Control block diagram of inverter
图3(b)给出了辅助桥臂的控制框图,其作用是将飞跨电容Cf1和Cf2的电压控制为Vdc/4,从而使A和B点电压保持平衡。Cf1和Cf2的电压被检测和反馈,并与Vdc/4的给定电压作比较,偏差经过比例调节器(KA和KB)产生两个归一化的控制变量(α1和α2),控制变量的极性由当前流入A和B点的净电流(iA′和iB′)决定。α1和α2被用于调节上下两个3L-FC的O1和O2状态的占空比(图中的dO1和dO2以及dO1′和dO2′),使得Cf1和Cf2被iA′和iB′充电或者放电,最终使其电压稳定在Vdc/4。流入A点和B点的净电流iA′和iB′通过两个电流传感器来实际检测(安装位置如图1所示),但在控制中只判断了它们的极性,并没有利用其幅值。
4 损耗分析
根据附录A表A1给出的额定参数,本文针对所提5L-NPC逆变器建立了一个仿真模型,对比分析了向O点注入不同大小的漂移电流后Rf的损耗。在仿真模型中,通过选择合适的电容值,使得Cf1,Cf2和Cf3上所有的电压偏差不超过5%。这样,在功率因数为1、调制度m=0.85的条件下,根据式(4)和式(6)可以估算出Rf的取值应大于0.9 Ω。选择Rf的值为2 Ω,根据式(7)计算可知,此时O点产生的电压偏差仅为100 V,小于1%Vdc。通过记录仿真的电流波形,对Rf的损耗PR进行数值计算的结果如附录C表C1所示,表中同时还给出了辅助桥臂的开关损耗Ploss-FLC以及5L-NPC的总损耗Ploss-NPC。表中:Im为相电流的峰值。
由附录C表C1可知,电阻Rf的损耗由漂移电流的大小来决定,在漂移电流为相电流峰值的5%时(这是一种非常严重的情况),其损耗仅占变流器整体损耗的4%,因此串入电阻Rf并不会带来过大的损耗。
5 实验验证
为了验证本文所提拓扑和相应的控制策略的正确性,搭建了一个3 kW的实验平台,并使用泰克DPO4104B(带宽1 GHz)4通道的存储式示波器对实验波形进行了记录,附录C图C1给出了实验平台的照片。
本次实验使用DSP和现场可编程门阵列(FPGA)板作为控制器,电网由市电电源表示,逆变器通过可调自耦变压器和隔离变压器连接到市电电源。在实验中,为了测试O点的平衡能力,在P点和O点之间通过一个开关并联了一个电阻器,通过提供一个失衡电流来模拟注入O点的直流漂移电流Idrift。附录C表C2给出了实验中主电路的配置和电气参数。
在功率因数为1、调制度m=0.85的条件下,根据式(1)可知,由5L-NPC流入A点电流的直流分量约等于2.4 A(相电流峰值为5 A),而在Cf1,Cf2和Cf3上所有的电压偏差不超过10 V条件下,根据式(4)和式(6)可以估算出Rf的取值应大于4.2 Ω。而Rf取值为5 Ω时,根据式(7)可知此时O点的电压偏差小于1.5%Vdc,因此实验中选取的串联电阻Rf为5 Ω。
由于5L-NPC逆变器的每相支路同时有4个IGBT或二极管串联导通,其通态压降对于低压实验的变流器会产生重要的影响,主要引起5次和7次电流谐波。实验中选择的50 A/600 V的IGBT的管压降约为1.2 V,4个IGBT的通态压降为4.8 V。假设产生的谐波全为5次谐波,4.8 V管压降将产生高于1 A的谐波电流,这相对于6 A的基波电流来说是很大的,将导致较差的总谐波失真(THD)性能。由于变流器的开关频率设置为2.5 kHz,其电流控制器的开环截止频率不会超过250 Hz,因此通过控制闭环来抑制谐波的能力比较弱。针对这个问题,有些文献提出了压降补偿的解决方案,例如文献[24]提出的通过调整脉宽调制(PWM)波的占空比来补偿压降的影响,但是需要考虑零序电流钳位的影响,控制方法复杂。本实验通过在回路中串入一定的电阻(实验中串联的等效电阻为4 Ω),这样管压降引起的5次谐波电流将被削弱近60%。同时,串入电阻还可以增加系统的阻尼,有助于系统的稳定性。由于并网控制策略并不是本文的重点,因此通过在滤波电感中串入小电阻的方法来改善波形,比较简单和有效。对于高压大电流的实际应用而言,器件管压降的影响是可以忽略的。
本文分别在功率因数λ=1和λ=0两种情况下对具有辅助桥臂的5L-NPC逆变器的A,B和O点电压平衡能力进行了测试。图4给出了λ=1条件下逆变器各中点电压的实验结果。实验首先测试了在m=0.85条件下不注入Idrift时中点A,B和O点的电压稳定性,随后向O点注入恒定的直流电流Idrift,测试了Cf3支路对O点的电压抗漂移能力进行测试,最后逐渐降低调制度m,对不同调制度下的平衡能力进行了测试。图4(a)为不注入Idrift时,P点与N点之间的电压VPN、A点与N点之间的电压VAN、B点与N点之间的电压VBN以及O点分别与P和N点之间的电压VPO和VON的电压波形。由图4(a)可知,VAN,VON和VBN分别稳定在300,200,100 V附近,说明在这种情况下A,B和O点电压能够被很好地平衡。图4(b)为注入Idrift后实验输出波形,在t1时刻,O和N之间的并联电阻Rd被接通,恒定的直流电流Idrift被注入O点(在Rd=800 Ω的条件下,Idrift值为5%峰值相电流,Idrift=0.25 A)。从图4(b)可以看到,在此过程中A和B点电压保持了平衡,而O点电压则从平衡点(200 V)偏离,稳态偏压ΔU约为4 V。说明Idrift注入后,A和B点电压平衡不会被影响,而O点电压漂移也能被抑制,但是由于Cf3串联电阻Rf的影响,会产生一个小的电压偏压ΔU。而ΔU除了受Rf的影响,还与调制度有关(如1.2节所述),图4(c)给出了在不同调制度下在注入与不注入Idrift情况下O点偏差电压的曲线图。由图4(c)可知,不注入Idrift时,在全调制度范围内O点均能实现平衡。注入Idrift后,在调制度m<0.65时O点产生的偏差随调制度的增加而增大,但在m>0.65以后,随着调制度增加而减小。这表明在λ=1的条件下,辅助桥臂对O点的电压漂移的抑制能力受调制度m的影响,且在高调制度下随调制度增加抑制能力增强。
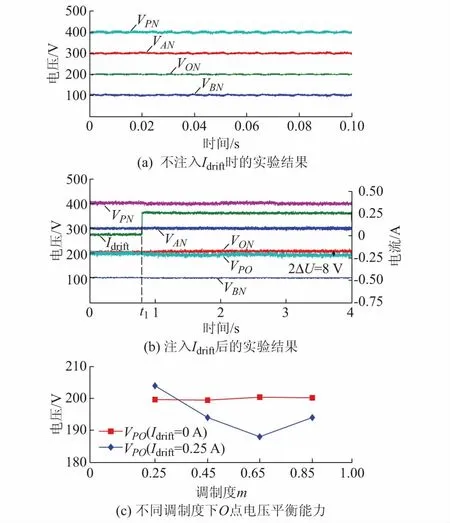
图4 λ=1条件下逆变器各中点电压的实验结果Fig.4 Experimental results of midpoint voltage under λ=1 condition
本文在λ=1的条件下,还对本文所提5L-NPC逆变器的稳态及动态并网控制性能做了测试,如图5(a)和图5(b)所示。图5(a)给出了稳态情况下的PWM相电压(uoa)波形和相电流(ia)的波形。由图5(a)可知,由于逆变器A,B和O点电压得到了良好的平衡控制,因此uoa具有均衡的5个电平,ia也含有较小的谐波含量。图5(b)给出了在λ=1和m=0.85的条件下,当电流给定值i*从2 A阶跃为3 A时逆变器的动态响应波形。由图5(b)可知,在t2时刻i*发生了阶跃,ia随之增加,由于此时逆变器从直流母线端吸收了更大的功率,因此直流母线电压VPN产生了一定程度的电压跌落,而VPO也随之跌落,但始终维持在VPN/2,说明动态过程中O点电压平衡能力不受影响。
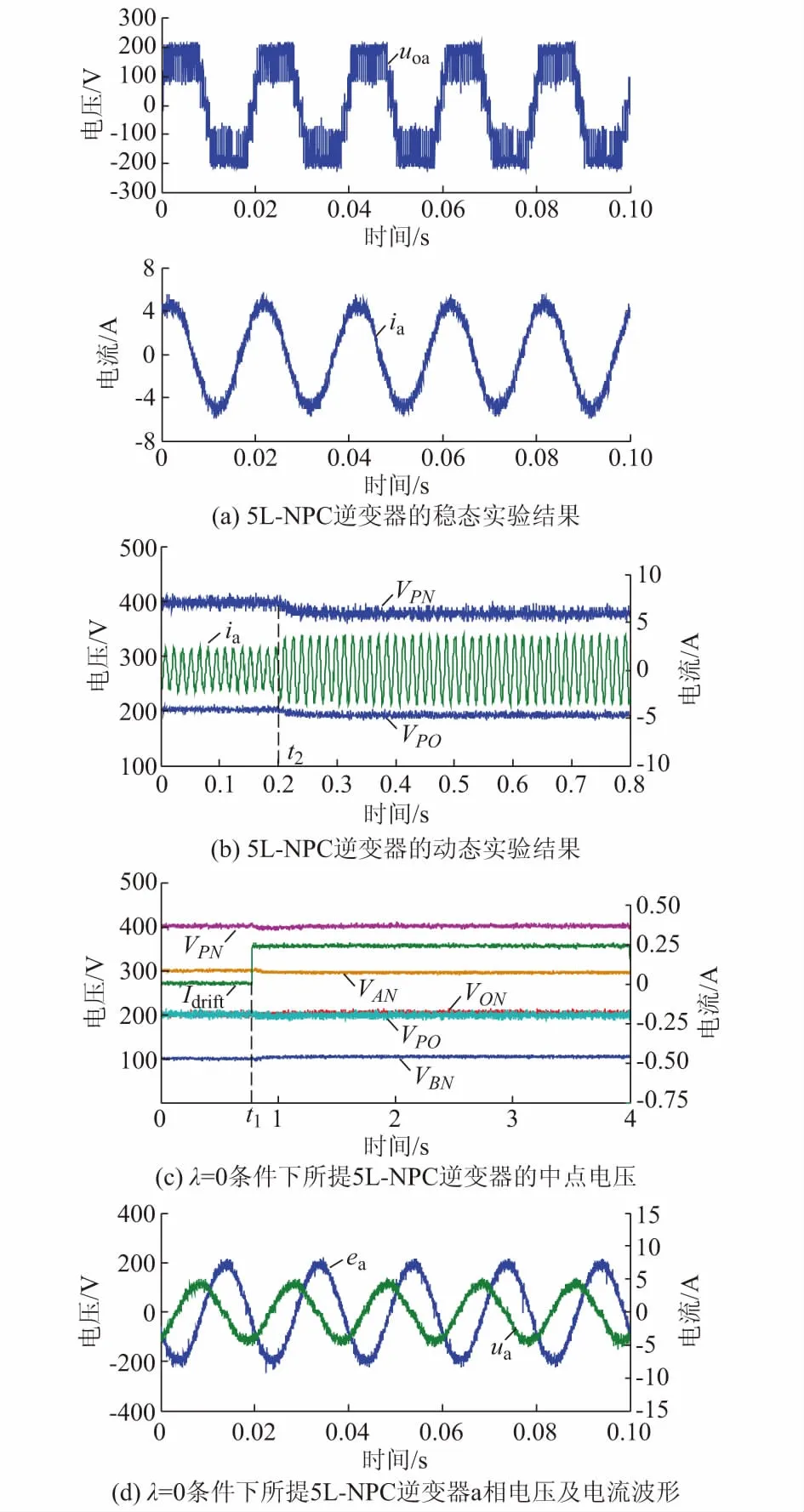
图5 逆变器的并网性能测试和λ=0条件下各中点电压的实验结果Fig.5 Grid-connected performance test of inverter and experimental results of midpoint voltage under λ=0 condition
在λ=0和m=0.85条件下,所提5L-NPC逆变器的平衡控制实验结果如图5(c)和(d)所示。由图5(c)和(d)可知,在t1时刻O点注入Idrift后,A,B以及O点电压均维持了良好的平衡,相电流与相电压波形接近理想正弦波。证明了所提5L-NPC逆变器在λ=0条件下,采用冗余矢量对调节占空比的调制策略可以有效实现对O点电压的平衡控制。
6 结语
本文所提的具有飞跨电容辅助桥臂的五电平逆变器可用于10 kV/5 MW以上等级的超大功率直驱风电变换系统,也可作为大功率高压光伏并网逆变器或无功补偿装置来使用。对于5L-NPC逆变器固有的中点电压不平衡问题,飞跨电容辅助桥臂可以有效解决A点和B点的电压平衡问题。对于O点的平衡问题,在高功率因数下,尽管受到飞跨电容Cf3中串联电阻Rf的影响,但是辅助桥臂仍然可以提供良好的平衡能力。在低功率因数下,调整冗余矢量占空比的控制策略可以为O点的电压平衡提供足够的支持。最后通过并网控制实验证明了本文提出的具有辅助桥臂的5L-NPC逆变器拓扑和控制方法的有效性。除了直流失衡,5L-NPC逆变器的O点还存在3倍基波频率的电压脉动,这种低频脉动对第4桥臂的工作是不利的。尽管可以通过选择大的直流母线电容来减小脉动电压的影响,但对其展开进一步的分析和研究对于本文所提的方案在大功率条件下的应用具有重要的意义。另外,本文只搭建了一个很小功率的实验装置来对所提的电路和控制方法进行了验证,而且采用串电阻来改善电流THD的做法,较为理想化。未来将采用更大功率的实验装置来对电流谐波、中点脉动的影响以及第4桥臂的性能进行检验。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] BLAABJERG F, MA K. Future on power electronics for wind turbine systems[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2013, 1(3): 139-152.
[2] BLAABJERG F, LISERRE M, MA K. Power electronics converters for wind turbine systems[J]. IEEE Transactions on Industry Applications, 2011, 48(2): 708-719.
[3] 屠卿瑞.模块化多电平换流器型直流输电若干问题研究[D].杭州:浙江大学,2013.
[4] 阳岳希,杨杰,贺之渊,等.基于MMC的背靠背柔性直流输电系统控制策略[J].电力系统自动化,2017,41(4):120-124.DOI:10.7500/AEPS20160728001.
YANG Yuexi, YANG Jie, HE Zhiyuan, et al. Control strategy of MMC based back-to-back HVDC transmission system[J]. Automation of Electric Power Systems, 2017, 41(4): 120-124. DOI: 10.7500/AEPS20160728001.
[5] 赵成勇,张宝顺,倪晓军,等.MMC-HVDC物理模拟系统的控制器架构设计[J].电力系统自动化,2015,39(6):68-74.DOI:10.7500/AEPS20140225003.
ZHAO Chengyong, ZHANG Baoshun, NI Xiaojun, et al. Controller architecture design for MMC-HVDC physical simulation system[J]. Automation of Electric Power Systems, 2015, 39(6): 68-74. DOI: 10.7500/AEPS20140225003.
[6] 肖志勇,盘宏斌,邓文浪,等.用于级联H桥整流器均压的新型多维空间矢量调制策略[J].电力系统自动化,2016,40(18):116-121.DOI:10.7500/AEPS20150205009.
XIAO Zhiyong, PAN Hongbin, DENG Wenlang, et al. Multidimensional space vector modulation strategy with voltage balancing capability for cascaded H-bridge rectifier[J]. Automation of Electric Power Systems, 2016, 40(18): 116-121. DOI: 10.7500/AEPS20150205009.
[7] 刘秋降,吴命利,吴丽然.级联H桥变流器电容电压均衡约束条件[J].电力系统自动化,2016,40(15):113-119.DOI:10.7500/AEPS20150613003.
LIU Qiujiang, WU Mingli, WU Liran. Constraints for balancing capacitor voltage of cascaded H-bridge converters[J]. Automation of Electric Power Systems, 2016, 40(15): 113-119. DOI: 10.7500/AEPS20150613003.
[8] RODRIGUEZ J, BERNET S, STEIMER P K, et al. A survey on neutral-point-clamped inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2219-2230.
[9] MA K, BLAABJERG F. Multilevel converters for 10 MW wind turbines[C]// Proceedings of the 2011-14th European Conference on Power Electronics and Applications, August 30-September 1, 2011, Birmingham, UK: 1-10.
[10] SENTURK O S, HELLE L, MUNK-NIELSEN S, et al. Medium voltage three-level converters for the grid connection of a multi-MW wind turbine[C]// European Conference on Power Electronics and Applications, September 8-10, 2009, Barcelona, Spain: 1-8.
[11] CHAVES M, MARGATO E, SILVA J F, et al. New approach in back-to-back m-level diode-clamped multilevel converter modelling and direct current bus voltages balancing[J]. IET Power Electronics, 2010, 3(4): 578-589.
[12] PAN Z, PENG F Z, CORZINE K A, et al. Voltage balancing control of diode-clamped multilevel rectifier/inverter systems[J]. IEEE Transactions on Industry Applications, 2005, 41(6): 1698-1706.
[13] MARCHESONI M, TENCA P. Diode-clamped multilevel converters: a practicable way to balance DC-link voltages[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4): 752-765.
[14] SHU Z, DING N, CHEN J, et al. Multilevel SVPWM with DC-link capacitor voltage balancing control for diode-clamped multilevel converter based STATCOM[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 1884-1896.
[15] SAEEDIFARD M, IRAVANI R, POU J. A space vector modulation strategy for a back-to-back five-level HVDC converter system[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2): 452-466.
[16] HOTAIT H A, MASSOUD A M, FINNEY S J, et al. Capacitor voltage balancing using redundant states of space vector modulation for five-level diode clamped inverters[J]. IET Power Electronics, 2010, 3(2): 292-313.
[17] ZHANG H B, FINNEY S J, FLETCHER J E, et al. DC-link capacitor voltage balancing for a five-level diode-clamped active power filter using redundant vectors[C]// Universities Power Engineering Conference, December 5-8, 2013, Christchurch, New Zealand: 1-6.
[18] SAEEDIFARD M, IRAVANI R, POU J. Control and DC-capacitor voltage balancing of a space vector-modulated five-level STATCOM[J]. IET Power Electronics, 2009, 2(3): 203-215.
[19] HATTI N, HASEGAWA K, AKAGI H. A 6.6 kV transformerless motor drive using a five-level diode-clamped PWM inverter for energy savings of pumps and blowers[J]. IEEE Transactions on Power Electronics, 2009, 24(3): 796-803.
[20] HASEGAWA K, AKAGI H. Voltage balancing of the four split DC capacitors for a five-level diode-clamped PWM inverter with a front-end diode rectifier[C]// Power Electronics Conference, June 21-24, 2010, Sapporo, Japan: 734-739.
[21] ASHAIBI A A, FINNEY S J, WILLIAMS B W, et al. Switched mode power supplies for charge-up, discharge and balancing DC-link capacitors of diode-clamped five-level inverter[J]. IET Power Electronics, 2010, 3(4): 612-628.
[22] ABDULLAH R, RAHIM N A, RAIHAN S R S, et al. Five-level diode-clamped inverter with three-level boost converter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5155-5163.
[23] CELANOVIC N, BOROYEVICH D. A fast space-vector modulation algorithm for multilevel three-phase converters[J]. IEEE Transactions on Industry Applications, 2001, 37(2): 637-641.
[24] NEACSU D O. Line voltage compensation for AC output converters[C]// 34th Annual Conference of IEEE Industrial Electronics, November 10-13, 2008, Orlando, FL, USA: 3149-3154.
魏米兰(1994—),女,硕士研究生,主要研究方向:大功率多电平变流器技术。E-mail: wmlxka1994@126.com
曾翔君(1976—),男,通信作者,博士,副教授,主要研究方向:大功率风电系统中功率变换和新能源等电力电子技术。E-mail: zengxj@mail.xitu.edu.cn
汪航(1991—),男,硕士研究生,主要研究方向:直驱风电系统电机控制和多电平变流器技术。E-mail: xjtuhw@126.com
