链式三角形静止同步补偿器子模块冗余容错方案

赵　宇, 苟锐锋, 涂小刚

(1. 西安西电电力系统有限公司, 陕西省西安市 710075; 2. 西安端怡科技有限公司, 陕西省西安市 710075)

0　引言

目前,国内电力电子技术朝着高压、大功率方向发展,柔性交流输电装置得到广泛应用。静止同步补偿器(static synchronous compensator,STATCOM)分为星形和三角形两种结构[1-2]。星形拓扑的容量较小,单机容量最大的案例为上海西郊±50 Mvar项目[3]。三角形拓扑STATCOM的最大单机容量可达±100 Mvar。近年来南方电网共有8套百兆乏级STATCOM投运[4-5],促进了高压大容量无功补偿技术的发展。

目前,链式星形拓扑的子模块冗余容错研究文献较多,主要集中在控制保护策略、旁路开关等技术的研究方面。由于三角形拓扑的功率等级较大,其冗余容错的文献、实验报道均较少。文献[6]给出了模块化多电平STATCOM的旁路开关、冗余控制与保护的技术要求,对基础理论研究具有指导意义。文献[7-8]研究了星形装置的子模块冗余方案,采用抬升直流电压来保持冗余恢复稳态后的调制比不变,并对三角载波进行变周期处理。由于三角形拓扑装置的直流电压环、调制方案与星形结构一致[9],因此该策略对两种拓扑均适用。文献[7]的研究表明,故障过渡过程中,电流的暂态调节时间约为30 ms,对控制系统的响应时间要求较高。文献[10]采用零序电压注入来改善星形装置的冗余过渡过程。根据各相故障情况、直流电压，实时计算出零序电压,再将其叠加至三相调制波,降低电流的扰动。文献[11]采用了零序电流注入来改善三角形装置的负载不平衡工况。但该方案通过直流电压产生零序电流指令,响应速度慢,电流调节时间大于50 ms,无法满足文献[7]的响应要求,故此种方案不适用于子模块冗余控制。

本文提出含虚拟阻抗技术的冗余容错控制策略,对故障扰动进行实时补偿。首先,给出了子模块冗余容错技术的参数指标、动作逻辑流程图,采用抬升直流电压、变三角载波技术保持稳态调制比不变。然后,阐述了动态虚拟阻抗的工作原理、实现方案。最后,给出了三角形 STATCOM的主回路参数、控制参数,建立PSCAD模型验证了新方案的有效性。

1　链式三角形STATCOM子模块冗余容错原理

1.1　冗余度的设计

链式三角形STATCOM的电路图见附录A图A1。其中,uga,ugb,ugc为电网电压;L为等效电感;udc为子模块电压;Cpm为电容;Rpm为放电电阻;iab,ibc,ica为角内电流。

国内某工程的百兆乏STATCOM的电路参数见附录A表A1,以下给出具体的参数性能分析。

首先,依据绝缘栅双极型晶体管(IGBT)器件参数、子模块电容的直流耐压水平,选取子模块额定电压udce=1 800 V。

其次,依据udce参数完成单相链式换流器的子模块数、冗余度、调制度范围等参数的计算。考虑装置交流侧输出的最大电压umax为:

umax=ulinepeak+ul

(1)

式中:ulinepeak为电网线电压峰值(取1.1倍过电压);ul为电抗器的电压分量(取1.3倍过电流)。

当ulinepeak=54 439 V，电流峰值Iep=1 346 A,电网基频ω0=314 rad/s时,可得umax=ulinepeak+1.3Iepω0L=62 131 V。

再通过调制度关系式可得:

umax=kmodNpmactudce

(2)

式中:kmod为调制度,无功补偿工程领域一般取kmod≤0.95;Npmact为不包含冗余的模块数。

由此可得Npmact=umax/udce/kmod=36。考虑10%的子模块冗余度,每相的总模块数为Npm=36+4=40。

1.2　冗余容错运行逻辑

对于H桥子模块,如果故障模块数小于冗余模块数,装置应能够持续运行[12],如图1(b)所示。图1中:PI表示比例—积分控制器;BSF表示二阶陷波器;PR表示比例—谐振控制器;CPS-SPWM表示载波相移正弦波脉宽调制。

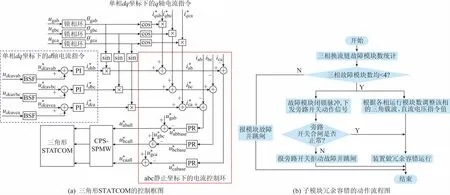
图1　子模块冗余容错的控制Fig.1　Control of sub-module redundant fault-tolerance

考虑到故障处理的快速性,子模块故障信息的汇总、开关输入/输出(I/O)逻辑判断、三角载波的动态调整由现场可编程门阵列(FPGA)实现[7];直流电流指令的抬升则由数字信号处理器(DSP)实现,控制周期Ts=100 μs。

1)检测故障、下发I/O信号耗时约几百微秒,开关合闸时间一般在5 ms以内。因此,旁路动作总延时约为6 ms。

2)DSP调整直流电压指令耗时1个控制周期,三角载波调整耗时小于50 μs,通信延时小于100 μs,算法调整的总延时小于300 μs。

三角载波调整的原理是:根据模块故障信息动态调节三角载波的周期[8,13],此方法能够保证等效开关频率不变。

2　传统的子模块冗余控制策略

2.1　电流控制环

三角形STATCOM的三相链式换流器之间并无耦合,一般采用单相静止坐标系模型进行控制[14]。式(3)给出了单相换流器的电路方程。

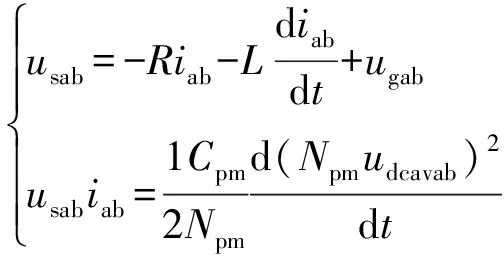
(3)

式中:R为单相换流器的等效电阻;ugab为电网线电压;usab为换流器输出的交流线电压;udcavab=udcab/Npm为子模块块电压的平均值,其中udcab为子模块电压和。式(3)的等效电路图见附录A图A2。

图1(a)中,每相采用独立的锁相环[15]。在电网电压畸变条件下,采用三相锁相环[16]需进行相角的简化,造成锁相角与实际相角存在差异;采用单相锁相环可提高相角精度,见附录A图A3至图A5的相关分析。BSF为二阶陷波器,它可滤除直流电压udcavab的二倍频谐波,见附录A图A6。

传统的控制环路分析如图2所示。图2(a)中,kpwm=ulinepeak/udcab为调制比;PR为包含50 Hz基波跟踪、150 Hz环流抑制[2]功能的控制器;Gopi(s)=1/(Ls+R)为电流开环传递函数。

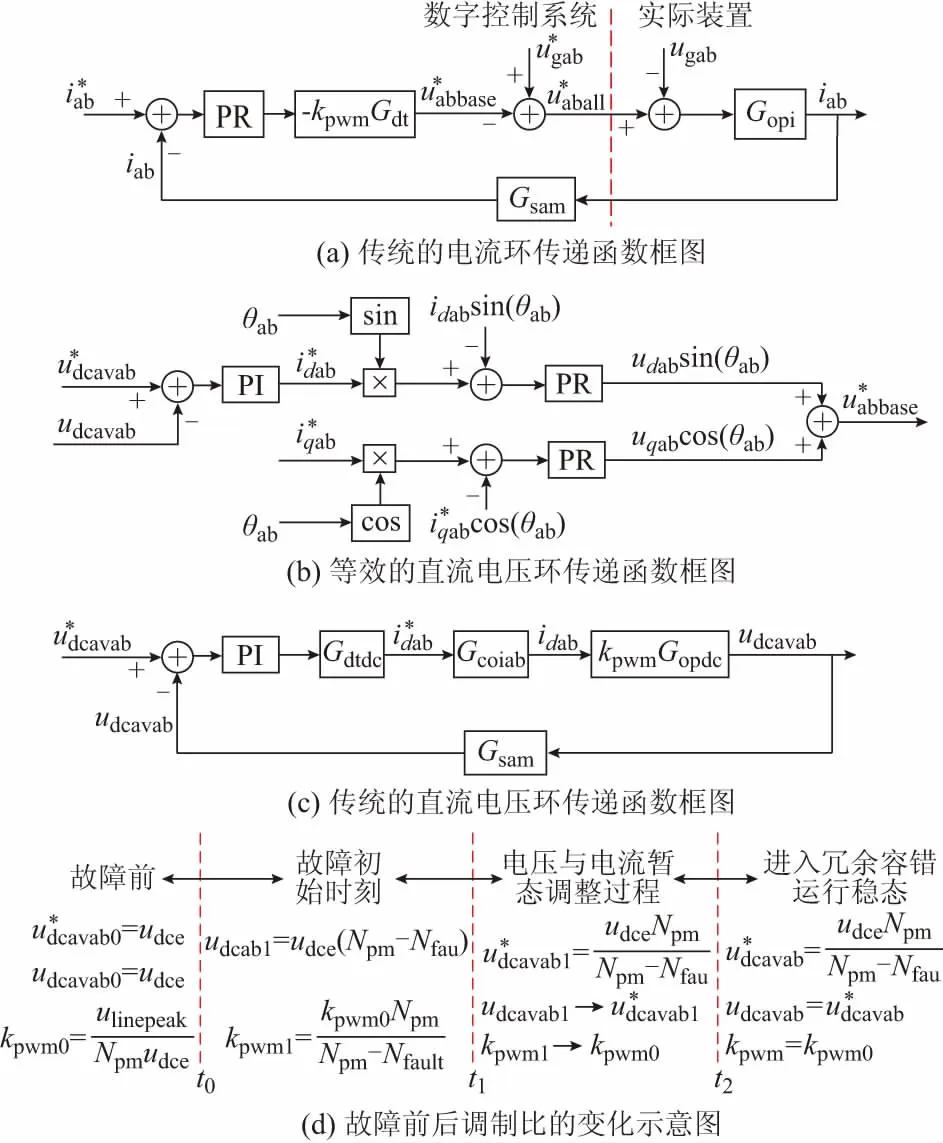
图2　传统的控制环路分析Fig.2　Analysis of traditional control loop

对于控制算法或通信产生的延时,一般将所有延时汇总成一阶低通滤波器[17]。控制周期为Ts,通信延时按50 μs处理,则利用Gdt(s)=1/(1.5Tss+1)替代电流环的延时。电流的采样延时由采样电路决定,可取采样延时为Gsam(s)=1/(0.2Tss+1)。

式(4)给出了PR调节器与电流闭环传递函数,PR调节器的波特图分析见附录A图A7。

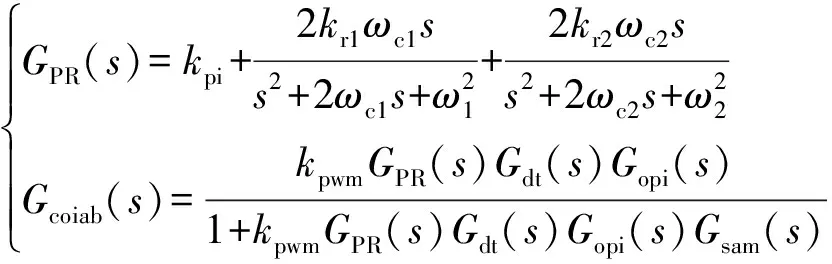
(4)

式中:变量取值见附录A表A2。

当子模块发生故障瞬间,实际工作的模块数为Npm-Nfau,由于子模块的电容电压不能瞬时突变,udcab减小为故障前的(Npm-Nfau)/Npm,则kpwm发生变化,传统的电流函数Gcoiab(s)发生突变。

2.2　直流电压控制环

图1(a)中存在dq轴变量的耦合,需将其等效为dq轴电流环路(见图2(b)),然后再对电压环进行分析。

将单相实际输入信号定位于α轴,并引入虚拟β轴[15],且β轴滞后于α轴π/2。于是有

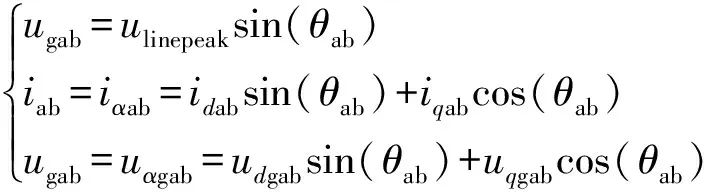
(5)

选取β轴变量为0,利用式(5)进行park变换,可得单相d-q坐标系的数学模型为:

(6)

式(3)是理想化的未考虑直流侧负载的电路方程,文献[18-19]给出了考虑子模块侧放电电阻等负载条件下的直流侧电路的平均模型。

根据功率平衡关系,交流侧功率应等于Npm个子模块直流电容输出的功率与负载功率之和,即

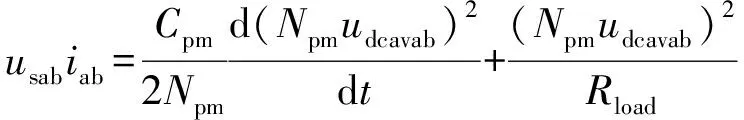
(7)

式中:Rload为负载电阻。

由于usabiab=udgabidab+uqgabiqab,于是有:

uqgabiqab

(8)

式中:Cpm/Npm为换流器的等效电容。选取d轴与电网电压同向,uqgab接近于零,并且kpwm=udgab/(Npmudcavab)。Rload产生的功率可做常数W处理。

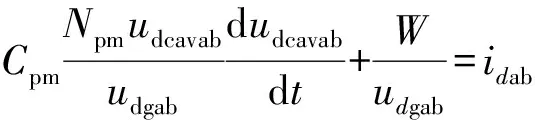
(9)

对式(9)取拉氏变换,可得:

(10)

图2(c)中,利用Gdtdc(s)=1/(Tss+1)替代电压控制环的算法的总延时,Gsam=1/(0.2Tss+1)为直流电压采样延时,则直流电压的闭环传递函数为:

Gcodc(s)=

(11)

其中

A1(s)=GPR(s)Gdt(s)Gopi(s)B1(s)=A1(s)Gsam(s)C1(s)=GPI(s)Gdtdc(s)Gopdc(s)D1(s)=C1(s)Gsam(s)

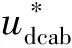
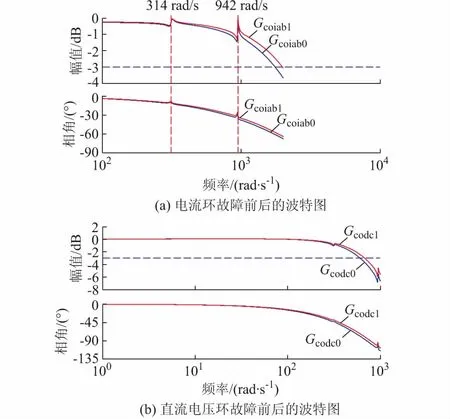
图3　故障前后的控制环波特图Fig.3　Control loop bode diagrams before and after failure

3　改进的冗余控制方案设计

3.1　故障的暂态过程分析

图2(d)给出了故障过程中调制比的变化过程。附录A表A2给出了控制参数,等效电阻R需依据损耗来计算,满载无功的效率为98.7%,则有功损耗为1.6%,损耗电阻为R=0.59 Ω。考虑到子模块等效电感等因素,取等效电感L=14.5 mH。

图2(a)中,电流环可分解为50 Hz环路和150 Hz环路。因此,电流环的带宽只有大于150 Hz才能同时对两种频率的电流指令进行正向跟踪。

目前我国产业风险评价体系还不够全面，对产业风险评价的使用还主要集中于贷前的风险识别阶段，主要是用于对客户企业进行风险分析，而未能延伸到贷中贷后的风险管理工作当中。但在当前产业结构升级的进程加速的背景下，银行在发放贷款和贷后管理时也面临着产业风险的快速改变，因此需要针对特定产业预先制定好风险应对方案，并及时对产业风险进行跟踪和管理，把控好产业风险，尽量减少风险损失。

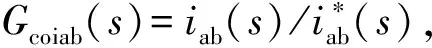
图1(a)中,BSF无法全部滤除100 Hz的谐波分量。因此,电压环的带宽应小于100 Hz。图3(b)两波特图的带宽均小于100 Hz(628 rad/s)。由于电压的主要分量位于0～20 Hz之间,此频率区间的幅值曲线在故障前后改变较小,对系统影响较小。如果电压存在大于20 Hz的扰动,则Gcodc1的增益变大,控制器的扰动增益上升,系统暂态性能变差。

3.2　采用动态虚拟阻抗改进系统传递函数

虚拟阻抗的原理来源于电路理论中的等效阻抗方法[22-23]。附录A图A8给出了两种虚拟阻抗方案,图A8(a)中,Z直接对控制器C的参数产生增益,改变了系统的阻抗[24]。图A8(b)中,Z不直接对控制器C产生增益,而是通过引入附加的前馈环路,改变系统的环路结构,达到改变传递函数的目的[21]。

图2(a)的电流控制环路中,PR控制器的参数多达6个,如果直接调节PR参数较为复杂。因此,本文采用附加前馈虚拟阻抗的方案。

增加前馈虚拟阻抗的电流环方案如图4(a)所示。图中:Gcoiab2和Gcodc2为加入虚拟阻抗的传递函数。

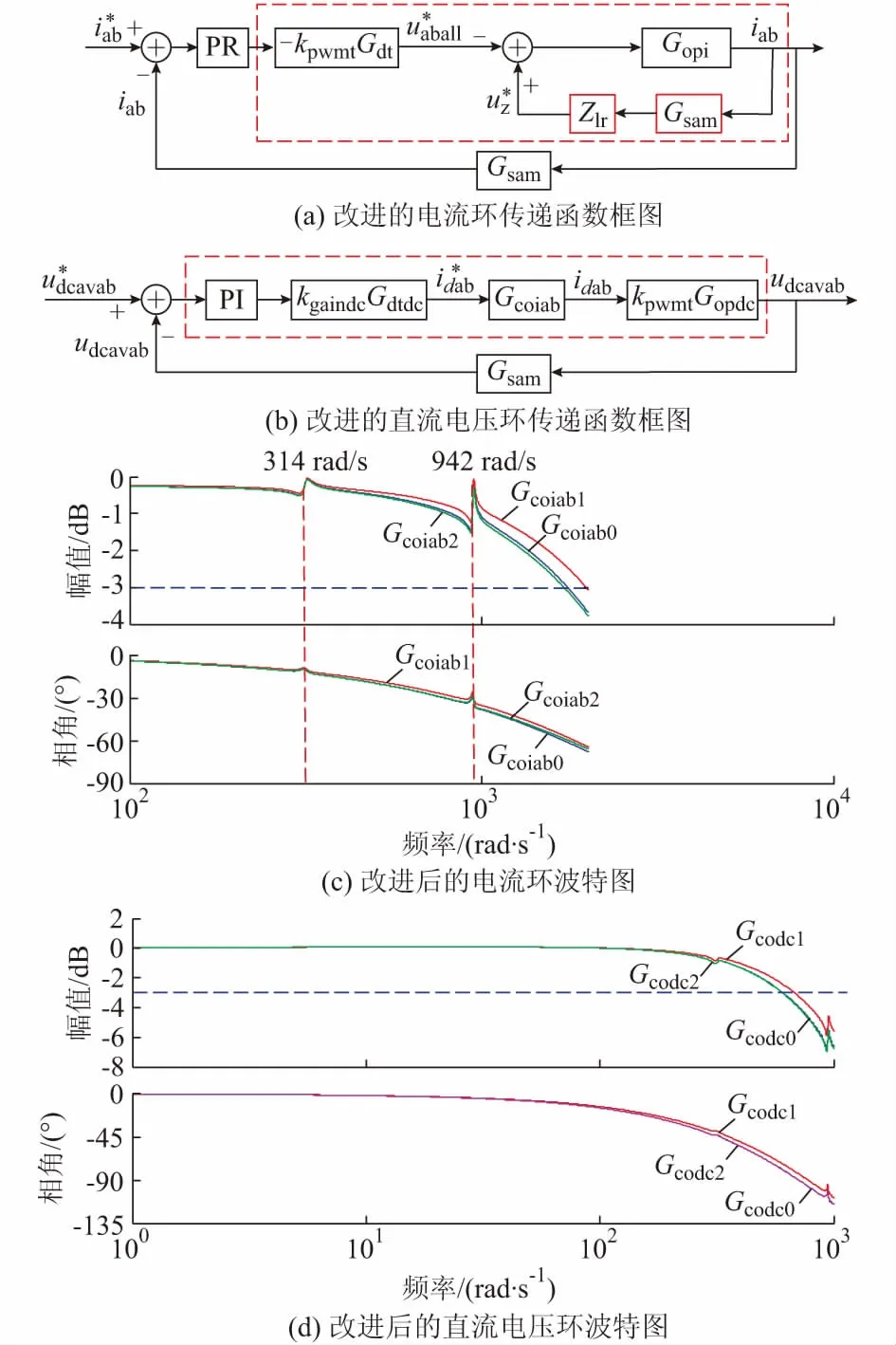
图4　改进后的控制环分析Fig.4　Analysis of improved control loop

图4中,Zlr为包含电阻、电感的虚拟阻抗。增加虚拟阻抗的目的是使虚线方框内的传递函数在故障前后相接近。设kpwmt为t时刻的调制比,其在故障前后保持实时计算更新。故障前的调制比为kpwm0,则故障前,虚线框内未加入Zlr的传递函数为:

Gw1(s)=kpwm0Gdt(s)Gopi(s)

(12)

故障后,虚线框内加入Zlr的传递函数为:

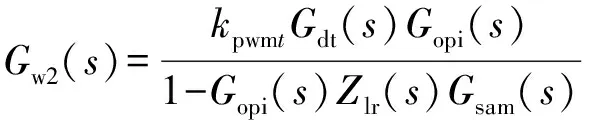
(13)

结合式(12)和式(13),虚拟阻抗的设计目标为Gw1(s)=Gw2(s),于是有:

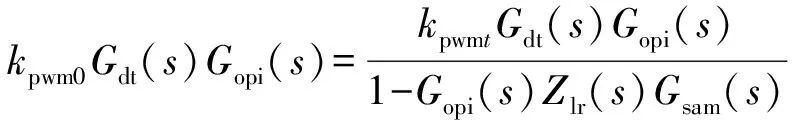
(14)

对式(14)进行分析,可求得Zlr的表达式为Zlr(s)=(1-kpwmt/kpwm0)/(Gopi(s)Gsam(s))。引入虚拟阻抗增益系数:

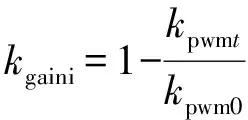
(15)

根据附录A表A2的参数可得:

Zls(s)=kgiani(0.014 5s+0.59)(0.2Tss+1)

(16)

考虑到二阶传递函数存在离散化延时问题,为简便起见,Zls(s)仍采用一阶传递函数:

Zls(s)=kgiani(0.014 5s+0.59)

(17)

对于式(17),为防止微分离散化计算出现高频突变,将其增加一阶低通滤波器进行优化,可得:

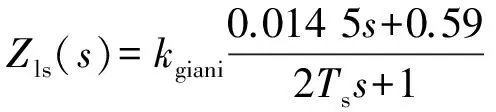
(18)

可见,当未发生故障时，kgaini=0,虚拟阻抗并不起作用;当发生4个模块故障瞬间,kgaini=-0.11。

附录A图A9中,当kgaini=-0.11时,Z1对应式(17),Z2对应式(18)。加入滤波器后,Z2的幅值曲线基本接近于Z1,但相角偏差增大。在50 Hz以内,两者的相角偏差小于5°,处于控制系统可补偿的范围之内。这说明式(18)可以较好地替代式(17)。

结合式(18)和式(4),可得到改进后的电流闭环传递函数为:

(19)

图2(c)的控制目标为直流电压,且PI参数只有两个。因此,采用动态调节PI参数的方法较简单。为了便于研究,图4(b)中认为经改进的Gcoiab(s)在故障前后是一致的。设计虚拟阻抗系数kgaindc保持虚线方框内的等效函数在故障前后相接近。

为了保持故障前后传递函数的一致性,则需满足:

kpwm0Gopdc=kgaindckpwmtGopdc

(20)

对式(20)进行分析,可得:

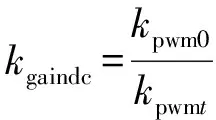
(21)

综合式(21)和式(11),可得改进的闭环传递函数为:

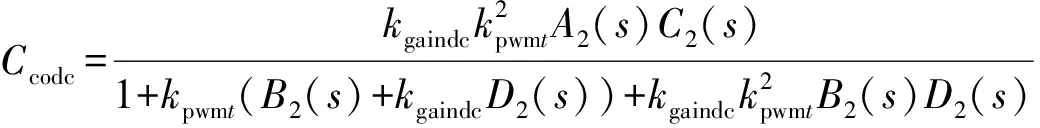
(22)

其中

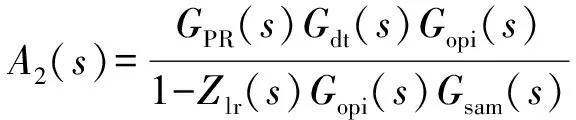
3.3　改进的系统传递函数波特图分析

附录A图A10给出了加入虚拟阻抗的总体控制框图。图4(c)中,在50,150 Hz附近,Gcoiab2与Gcoiab0的幅值非常接近,偏差小于0.03 dB;Gcoiab2与Gcoiab0的相角曲线也十分接近,偏差小于1°。虚拟阻抗的引入使得故障前后电流环的波形基本保持一致。

图4(d)中,在小于20 Hz或大于20Hz的区域内,Gcodc2与Gcodc0的幅值偏差小于0.02 dB,相角偏差小于0.5°,这说明虚拟阻抗的补偿效果较为理想。

4　算例分析

4.1　仿真电路

采用附录A表A1至表A3的参数,利用PSCAD软件建立±100 Mvar STATCOM的仿真模型,见附录B图B1。其中,脉冲发生周期为10 μs,闭环控制周期为100 μs,电流采样周期为20 μs。子模块的故障设置如下:0.9 s设置三相均产生4个子模块故障,立即封锁脉冲;脉冲封锁后,进行调整三角载波、直流电压指令处理;0.906 s旁路开关合闸完毕,所有的故障模块被旁路。

4.2　仿真结果

仿真结果见图5和附录B图B2至图B6。传统方案的波形下标为1,新方案的波形下标为2。本文的调节时间是指从故障时刻开始,直至输出的电气量达到并稳定在目标值的5%范围内所用的时间。

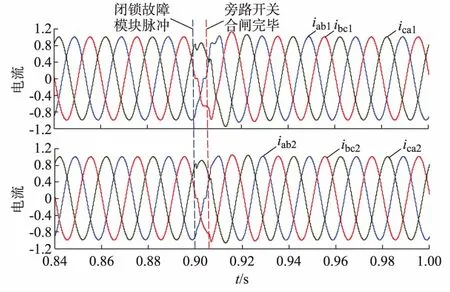
图5　改进前后装置的线电流波形对比Fig.5　Comparison of wire current waveforms before and after improvement

从图5可以看出:在故障模块闭锁瞬间,传统方案的电流发生轻微抖动;由于实时计算虚拟阻抗,改变了脉宽调制(PWM)电压输出,新方案对电流突变有一定的抑制作用。在旁路开关合闸完毕后,传统方案的电流扰动增益较大,电流畸变较为严重,最低幅值约为0.78(标幺值),最高幅值约为1.16;新方案较好地抑制了电流畸变,电流幅值最低为0.9左右,最高超调点约为1.04。传统方案的暂态调节时间约为30 ms,新方案的暂态调节时间约为25 ms。

从附录B图B2可以看出:传统方案的无功功率变化较为剧烈,最低幅值为0.75(标幺值)左右,最高幅值约为1.16。新方案的无功最低幅值约为0.89,最高幅值约为1.04。由于存在直流电压的爬升,新旧方案均出现长时间的有功突变,但新方案的恢复速度较快(约为40 ms)。

从附录B图B3可以看出:在故障子模块的闭锁、旁路开关合闸瞬间,输出调制电压的电平数发生突变,传统方案存在较大的扰动,电平的突变较为严重;新方案的调制电压正弦度较好,过渡过程较为平滑。

附录B图B4中,在故障子模块的闭锁、旁路开关合闸瞬间,BSF未完全滤波掉的100 Hz谐波突变增大,传统方案的扰动较大,幅值波动约0.03(标幺值),经50 ms由1抬升至1.11左右。新方案的幅值波动降低为0.02,经40 ms由1抬升至1.11左右。附录B图B5中,未进行滤波的电压含有较多的100 Hz谐波,幅值约为0.05。新方案的直流电压收敛速度、波动幅值均得到一定程度的改善。

附录B图B6中,电流虚拟阻抗系数对应式(15);电压虚拟阻抗系数对应式(21)。在0.9 s之前未发生故障,阻抗系数接近于0。0.9 s发生故障瞬间,电流的阻抗系数变为-0.11,电压的阻抗系数变为0.9,虚拟阻抗对传递函数进行调整。0.94 s后,系统进入稳态,阻抗系数的幅值再次趋近于零。

5　结语

本文分析了常规冗余技术对三角形STATCOM的适应能力,指出冗余动作延时、直流电压抬升是引发系统暂态振荡的主要原因;提出动态虚拟阻抗技术对直流电压环、电流环进行改进,削弱由调制比突变引发的系统振荡。仿真结果表明,所述新方案比传统方案在优化暂态过渡过程方面具有优势。交流电压的故障工况较为复杂,本文暂未涉及相关的内容,这些工作有待于进一步的深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 季振东,孙毅超,李东野,等.星形和三角形连接的链式H桥STATCOM不平衡补偿分析[J].高电压技术,2015,41(7):2435-2443.

JI Zhendong, SUN Yichao, LI Dongye, et al. Comparative analysis for unbalance compensation of cascaded H-bridge STATCOMs between star and delta configuration[J]. High Voltage Engineering, 2015, 41(7): 2435-2443.

[2] 宋强,魏伟,黎小林,等.三角形连接链式STATCOM三倍频环流优化研究[J].电网技术,2015,39(8):2364-2370.

SONG Qiang, WEI Wei, LI Xiaolin, et al. Optimization of the triple-harmonic circulating current for delta-connected cascaded STATCOM[J]. Power System Technology, 2015, 39(8): 2364-2370.

[3] 张洪涛,宋强,刘钟淇,等.±50 Mvar链式STATCOM的实时数字仿真[J].电力系统自动化,2006,30(17):19-23.

ZHANG Hongtao, SONG Qiang, LIU Zhongqi, et al. Real-time digital simulation of a ±50 Mvar cascaded STATCOM[J]. Automation of Electric Power Systems, 2006, 30(17): 19-23.

[4] 李春华,黄伟雄,袁志昌,等.南方电网±200 Mvar链式STATCOM系统控制策略[J].电力系统自动化,2013,37(3):116-121.

LI Chunhua, HUANG Weixiong, YUAN Zhichang, et al. Systematic control strategies for ±200 Mvar cascaded STATCOM in China Southern power grid[J]. Automation of Electric Power Systems, 2013, 37(3): 116-121.

[5] 张言权,刘洋.±200 Mvar链式静止同步补偿器保护功能设计[J].电力系统自动化,2015,39(20):152-157.DOI:10.7500/AEPS20141229008.

ZHANG Yanquan, LIU Yang. Protection design for ±200 Mvar cascade STATCOM[J]. Automation of Electric Power Systems, 2015, 39(20): 152-157. DOI: 10.7500/AEPS20141229008.

[6] 连霄壤,江道灼. 基于模块化多电平的静止无功补偿器故障容错控制[J].电力系统保护与控制,2012,40(16):83-89.

LIAN Xiaorang, JIANG Daozhuo. Fault-tolerant design and control of modular multilevel converter-based STATCOM[J]. Power System Protection and Control, 2012, 40(16): 83-89.

[7] SONG Wenchao, HUANG A Q. Fault-tolerant design and control strategy for cascaded H-bridge multilevel converter-based STATCOM[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2700-2708.

[8] 许胜,赵剑锋,许杏桃.改进型级联H桥型DSTATCOM装置n+1冗余容错控制策略[J].电力自动化设备,2010,30(7):54-59.

XU Sheng, ZHAO Jianfeng, XU Xingtao. Improvedn+1 redundant fault-tolerant control strategy of cascaded H-bridge DSTATCOM[J]. Electric Power Automation Equipment, 2010, 30(7): 54-59.

[9] 史丽萍,曹雪祥,陈丽兵,等.改进的STATCOM相内直流电容电压平衡控制策略[J].电力系统自动化,2015,39(2):119-125.DOI:10.7500/AEPS20130526003.

SHI Liping, CAO Xuexiang, CHEN Libing, et al. An improved DC capacitor voltage balance control strategy among phases for STATCOM[J]. Automation of Electric Power Systems, 2015, 39(2): 119-125. DOI: 10.7500/AEPS20130526003.

[10] LEE C, CHEN H, WU P, et al. A fault tolerant operation technique for STATCOMs based on star-connected cascaded H-bridges multilevel converter[C]// IEEE Applied Power Electronics Conference and Exposition, March 15-19, 2015, Charlotte, NC, USA: 995-1001.

[11] HAGIWARA M, MAEDA R, AKAGI H. Negative-sequence reactive-power control by a PWM STATCOM based on a modular multilevel cascade converter (MMCC-SDBC)[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 720-728.

[12] 武文,吴学智,荆龙,等.模块化多电平变流器子模块故障容错控制策略[J].电网技术,2016,40(1):11-18.

WU Wen, WU Xuezhi, JING Long, et al. A fault-tolerated control strategy for sub-module faults of modular multilevel converters[J]. Power System Technology, 2016, 40(1): 11-18.

[13] XIONG Liansong, MA Luyao, ZHUO Fang,et al. Seamless self-healing control strategy for cascaded multilevel STATCOM[C]// 2011 International Conference on Advanced Power System Automation and Protection, October 16-20, 2011, Beijing, China.

[14] 刘钊,刘邦银,段善旭,等.系统电压不平衡下链式静止同步补偿器控制研究[J].中国电机工程学报,2011,31(9):1-7.

LIU Zhao, LIU Bangyin, DUAN Shanxu, et al. Research on cascade multilevel STATCOM under unbalanced system voltage[J]. Proceedings of the CSEE, 2011, 31(9): 1-7.

[15] 李明,王跃,方雄,等.无正交虚拟信号生成的单相DQ锁相环研究[J].中国电机工程学报,2011,31(15):27-32.

LI Ming, WANG Yue, FANG Xiong, et al. Research on single-phaseDQphase-locked loop without imaginary signal generation[J]. Proceedings of the CSEE, 2011, 31(15): 27-32.

[16] 刘锋.电网不平衡下三相锁相环研究[D].成都:电子科技大学,2013.

[17] 张兴,张崇巍.PWM整流器及其控制[M].北京:机械工业出版社,2012.

[18] 刘闯,支月媚.混合级联式电力电子变压器拓扑结构及控制策略[J].电网技术,2017,41(2):596-603.

LIU Chuang, ZHI Yuemei. Hybrid cascaded power electronics transformer topology and control scheme[J]. Power System Technology, 2017, 41(2): 596-603.

[19] 何英杰,付亚彬,段文岩.一种三角形联结串联H桥SVG直流侧电压控制方法研究[J].电工技术学报,2015,30(9):70-78.

HE Yingjie, FU Yabin, DUAN Wenyan. Research on DC voltage control method of delta connection cascaded H bridge SVG[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 70-78.

[20] 谢震,张兴,杨淑英,等.基于虚拟阻抗的双馈风力发电机高电压穿越控制策略[J].中国电机工程学报,2012,32(27):16-22.

XIE Zhen, ZHANG Xing, YANG Shuying, et al. High voltage ride-through control strategy of doubly fed induction wind generators based on virtual impedance[J]. Proceedings of the CSEE, 2012, 32(27): 16-22.

[21] 张兴,朱云国,刘淳,等.无刷双馈发电机双向变换器内模-前馈复合控制方案[J].电力系统自动化,2013,37(2):11-16.

ZHANG Xing, ZHU Yunguo, LIU Chun, et al. Internal model and feedforward composite control scheme design of the brushless doubly-fed generator back to back converter[J]. Automation of Electric Power Systems, 2013, 37(2): 11-16.

[22] 周武,乐健,杨金涛,等.中压动态电压恢复器的虚拟阻抗控制策略[J].电网技术,2016,40(8):2525-2531.

ZHOU Wu, LE Jian, YANG Jintao, et al. Control strategy of MV dynamic voltage restorer as virtual impedance[J]. Power System Technology, 2016, 40(8): 2525-2531.

[23] 郭倩,林燎源,武宏彦,等.考虑自适应虚拟阻抗的微电网分布式功率控制策略[J].电力系统自动化,2016,40(19):23-29.DOI:10.7500/AEPS20151206001.

GUO Qian, LIN Liaoyuan, WU Hongyan, et al. Distributed power control strategy for microgrids considering adaptive virtual impedance[J]. Automation of Electric Power Systems, 2016, 40(19): 23-29. DOI: 10.7500/AEPS20151206001.

[24] 吕志鹏,罗安.不同容量微源逆变器并联功率鲁棒控制[J].中国电机工程学报,2012,32(12):35-42.

LÜ Zhipeng, LUO An. Robust power control of paralleled micro-source inverters with different power ratings[J]. Proceedings of the CSEE, 2012, 32(12): 35-42.

赵宇(1985—),男,通信作者,硕士,工程师,主要研究方向:柔性直流输电与大功率电力电子技术。E-mail： zhaoyu_u@163.com

苟锐锋(1959—),男,教授级高级工程师,主要研究方向:高压直流输电与柔性直流输电技术。E-mail: gourf@xdps.com.cn

涂小刚(1980—),男,高级工程师,主要研究方向:柔性直流输电控制保护技术。E-mail: xdpstxg@163.com