混合型模块化多电平换流器解析建模与功率运行区间分析

鲁晓军, 向　往, 林卫星,2, 文劲宇

(1. 强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院), 湖北省武汉市 430074;2. 特变电工新疆新能源股份有限公司, 新疆维吾尔族自治区乌鲁木齐市 830011)

0　引言

基于半桥型子模块(HBSM)和全桥型子模块(FBSM)的混合型模块化多电平换流器(MMC)具备交直流解耦控制能力,能不闭锁穿越直流故障[1-2],在架空线柔性直流输电领域[3-8]具有广阔的应用前景,近年来引起了国内外学者的广泛关注[9-16]。

在混合型MMC子模块比例设计方面,文献[1]根据最大调制比和直流故障期间无功功率控制需求,提出了确定混合型MMC桥臂子模块最小数量和FBSM的最小数量的方法。文献[2]从子模块均压需求和阻断直流故障的角度提出了FBSM的设计原则。文献[9]根据混合型MMC要求的低电压输出水平和桥臂子模块均压要求,提出了桥臂HBSM和FBSM数量的计算方法。在混合型MMC运行控制方面,文献[1]提出了正常运行工况下阀段的电容电压平衡控制。文献[2]提出了子模块均压控制策略,分析了子模块电容电压波动和电容设计原则。文献[10]提出了子模块分组充电启动策略和直流故障穿越控制与恢复策略。文献[11]研究了双极短路和单极对地短路故障穿越策略。文献[12]提出了直流单极接地故障穿越控制策略,避免了故障期间阀侧直流电压偏置。文献[13]提出了对称单极接线的混合型 MMC的分极控制策略,使得换流器可以在单极接地故障下保持健全极持续运行。文献[14]针对整流站采用电网换相换流器(LCC),逆变站采用混合型MMC的混合直流输电系统,在文献[9]的基础上分析了FBSM的选取原则,并通过控制直流电流实现直流故障穿越。文献[15]提出了混合型MMC直流故障期间限制故障电流并维持向交流系统输出无功功率的控制策略。文献[16]针对应用于低压配电网的低电平数混合型MMC,为减少输出谐波,提出了一种改进调制方法。

可见,目前已有文献大多针对混合型 MMC的子模块比例设计、桥臂子模块能量均衡控制和直流故障穿越控制等方面展开研究,鲜有文献涉及混合型MMC的解析建模。换流器解析模型是定量研究换流器运行特性、换流站主回路参数设计和主回路状态计算等方面的理论基础。关于MMC的解析建模与稳态特性研究,目前大多文献均以桥臂全部采用HBSM的半桥型MMC为研究对象[17-24]。而混合型 MMC在桥臂中引入了可输出负电平的FBSM,其拓扑构成与半桥型MMC有较大差别;混合型MMC在桥臂调制信号中引入了直流调制比[9],可运行于低直流电压甚至负直流电压。低直流电压下运行时,还需要避免单向桥臂电流导致半桥子模块无法正常均压。因此混合型MMC的调制和控制策略均与半桥型MMC有很大不同,无法将半桥型MMC的解析模型直接应用于混合型MMC,有必要对混合型MMC解析模型与运行特性进行研究。

基于文献[9]的混合型MMC基本控制框架和文献[24]提出的半桥型MMC动态相量模型,本文推导了考虑混合型MMC内部电气动态和调制信号的动态解析模型和稳态解析模型。通过对比动态和稳态解析模型的计算结果与电磁暂态模型的仿真结果,验证了动态和稳态解析模型的精确性。提出了混合型MMC在任意直流电压水平下功率运行区间的计算方法,考虑了子模块电容电压波动范围约束、桥臂电流最大值约束以及半桥子模块均压约束等多种运行约束条件,计算了不同直流电压水平下混合型MMC的功率运行区间,并分析了各约束条件和子模块电容、桥臂电抗器、桥臂子模块比例等参数对运行区间的影响。

1　混合型 MMC解析模型

1.1　混合型MMC拓扑与控制

混合型MMC的单相示意图如图1所示。其每相桥臂均由全桥子模块和半桥子模块串联而成。图1中,混合型MMC的桥臂用等效受控电压源串联阻抗表示,up和un分别为上、下桥臂输出电压,Rarm和Larm分别为桥臂等效电阻及桥臂电感。交流变压器与交流系统的等效电路在图中也一并给出。

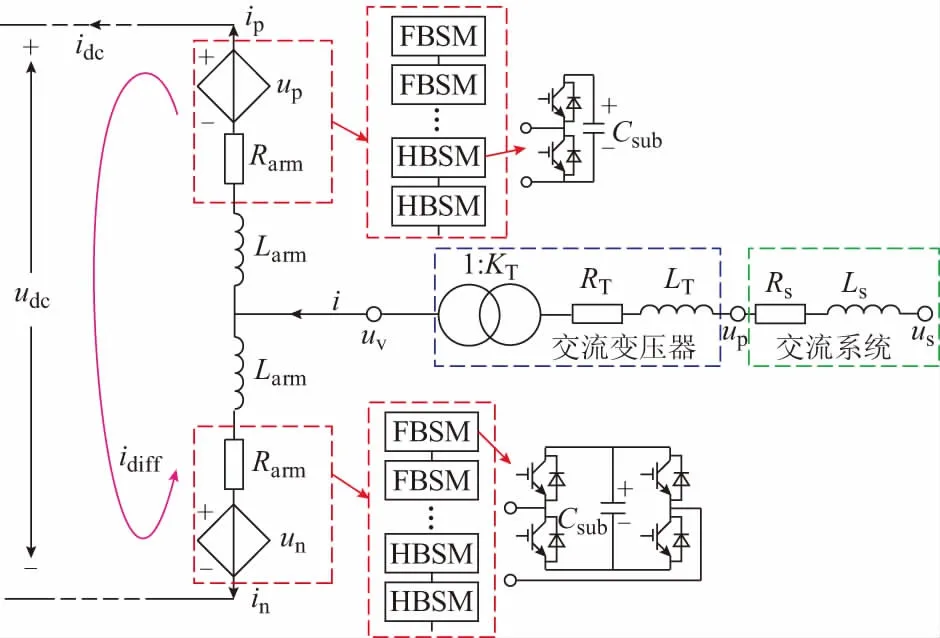
图1　混合型MMC单相示意图Fig.1　Single phase schematic diagram of hybrid MMC

混合型MMC的基本控制[9]如图2所示。其中,uc,avg为桥臂子模块电容平均电压,即其直流分量,用于桥臂能量均衡控制;Idref,Iqref和Idpu,Iqpu分别为交流电流d轴和q轴分量的参考值及标幺值;Idcref和Idcpu分别为直流电流的参考值和标幺值。相比半桥型MMC的基本控制,混合型MMC的基本控制配备了直流电流控制回路和桥臂能量均衡控制回路。根据混合型MMC运行需要,桥臂的调制信号中包含直流调制信号mdc(t)、基频交流调制信号m(t)和二倍频交流调制信号mdiff(t)。mdc(t),m(t),mdiff(t)分别用于控制直流电流、基频交流电流和抑制桥臂环流二倍频分量。

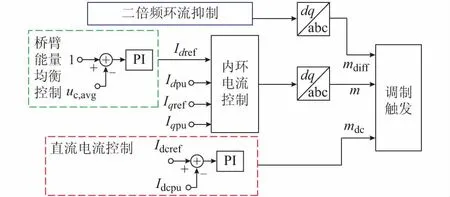
图2　混合型MMC基本控制框图Fig.2　Elementary control diagram of hybrid MMC

1.2　混合型MMC动态解析模型

记直流额定电压为UdcN,子模块额定电压为ucN,则每桥臂所含的子模块总数Nsm(不考虑冗余)为:

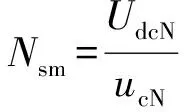
(1)

混合型MMC的上、下桥臂的调制信号mp(t)和mn(t)可以表示为:

(2)

相比半桥型MMC,混合型MMC的桥臂调制信号中增加了直流调制比这一控制量,如式(2)等号右边第一项所示。

上、下桥臂输出电压up和un可以表示为:

(3)

记上、下桥臂电流分别为ip和in,方向如图1中所示。定义idiff为桥臂环流,其可根据上、下桥臂电流计算,表达式为:

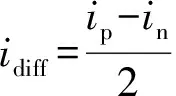
(4)

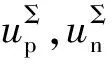
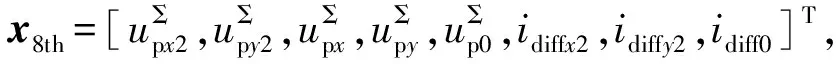
附录A式(A2)可以进一步简写成:

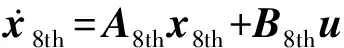
(5)

式(5)即为旋转坐标系下混合型MMC的8阶动态模型。分析矩阵A8th的元素,可知其主要包含混合型 MMC的电气参数(Carm,Rarm,Larm)以及调制信号各频率分量的坐标轴分量Mdc,Mx,My,Mx2和My2。

定义桥臂交流侧內电势为下桥臂与上桥臂输出电压之差的一半,静止坐标系下桥臂內电势ev为:

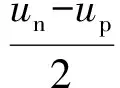
(6)

根据式(6)可得旋转坐标系下桥臂内电势ev表达式为:

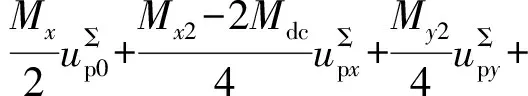
(7)

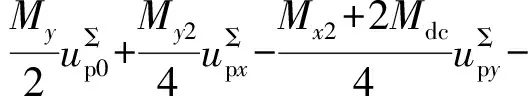
(8)

1.3　混合型MMC稳态解析模型

将1.1节中动态模型式(5)的左侧状态变量的导数项置零,即可得到混合型MMC在旋转坐标系下的稳态解析模型,该稳态模型包含8个代数方程,可表示为:

0=A8thx8th+B8thu

(9)

上述8个代数方程的具体表达式不再赘述。在下文中,各变量的下标加“0”以表示稳态值。求解稳态模型即利用式(9)的8个非线性代数方程求解模型的全部未知变量。

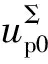
1)已知交流侧电流ix0和iy0

若已知条件为交流侧电流ix0和iy0,则可先根据交流侧电路求出桥臂內电势evx0和evy0,再根据式(7)和式(8)构造2个等式约束条件,即可求出全部变量。为了计算桥臂內电势,引入混合型MMC交流侧等效电路,如附录B图B1所示,其与半桥型MMC交流侧等效电路相同。其中LT和RT分别为交流变压器的等效漏电感和电阻,KT为交流变压器变比,Ls和Rs分别为交流系统等效内电感和内电阻。

从交流侧等效电路分析,根据KVL可以得到利用交流侧电流计算桥臂內电势ev的表达式为:

(10)

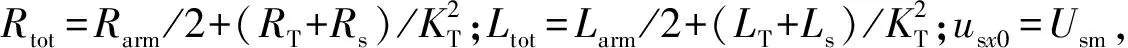
2)已知公共连接点(PCC)有功、无功功率

若已知条件为PCC点的有功功率P0和无功功率Q0,根据式(11)和式(12)可先求出ix0和iy0,进而利用前述方法求出全部未知变量。

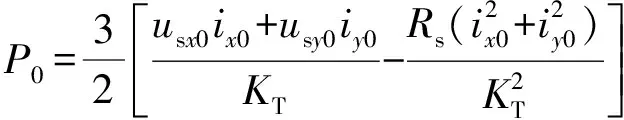
(11)

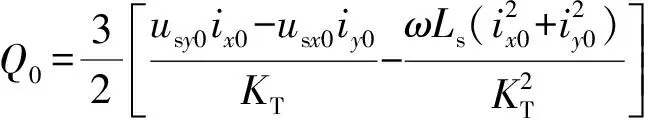
(12)

3)已知条件为直流电流和无功功率

若已知条件为直流电流idc0和无功功率Q0,考虑到桥臂环流的直流分量idiff0与直流电流idc0在稳态时存在如下关系:

idc0=3idiff0

(13)

利用式(12)和式(13)可以构造出2个等式约束方程,进而求解全部未知变量。

当已知条件为其他情况时,可以类似地构造出2个等式约束方程,进而对稳态模型进行求解。

2　解析建模仿真验证

2.1　测试系统参数

测试系统拓扑结构及参数见附录B图B2及附录A表A1。本节以该测试系统为例,对混合型MMC解析模型精确性进行验证,其中,混合型MMC每个桥臂全桥子模块与半桥子模块数目比例为1∶1。

2.2　动态解析模型精确性验证

根据附录A式(A2),在Simulink/MATLAB平台下搭建了测试系统的动态解析模型,并建立了相应的控制器模型,测试系统采用定直流电流和定无功功率控制,并投入二倍频环流抑制器。在PSCAD/EMTDC平台下相应搭建了测试系统的等值电磁暂态模型[25-26],所用控制器及其参数与动态解析模型相同。等值电磁暂态模型中,MMC每个桥臂采用两个受控电压源,分别代表全桥子模块组合和半桥子模块组合,受控电压源的输出电压机理考虑了子模块排序算法及子模块电容的充放电动态[25-26]。

为验证动态解析模型的精确性,对于测试系统做了如下动态特性仿真:2 s时直流电压以每秒-2(标幺值)的速度下降至0;2.05 s时直流电流指令值从-1(标幺值)以每秒5的速度减小到0;2.75 s时无功功率指令值从-0.1(标幺值)以每秒1的速度增大到-0.3。这一过程中电磁暂态模型与动态解析模型的响应曲线如附录B图B3所示,以A相上桥臂为例,图B3(a)至(c)分别展示了桥臂总电容电压、桥臂电流和直流电流的波形。可以看到,电磁暂态模型与动态解析模型的响应曲线吻合度很高,从而验证了本文所提出的动态解析模型的正确性。

2.3　稳态解析模型精确性验证

由于在正常额定直流电压水平下,混合型MMC与半桥型MMC运行特性没有较大区别,为验证本文所提出的混合型MMC稳态解析模型的精确性,以A相上桥臂子模块总电容电压、桥臂输出电压、桥臂电流为例,对比了50%额定直流电压、20%额定直流电压和零直流电压下等值电磁暂态模型的仿真结果与稳态解析模型的计算结果,如附录B图B4所示。仿真模型和解析模型中换流器均考虑投入桥臂二倍频环流抑制控制策略,直流电流参考值为0,换流器向交流系统输出0.1的无功功率。利用稳态解析模型求解各电气量与控制量时对应已知条件为直流电流idc0和无功功率Q0。从图B4中可以看到,稳态解析模型的计算结果与电磁暂态模型的仿真结果高度吻合,验证了本文所提出的稳态解析模型的精确性。

3　混合型MMC运行区间分析

换流站的功率运行区间是实际工程中较为关注的技术指标之一,由于换流站在运行中需要满足电气量和控制量的各项约束条件,因此考虑各项约束条件下的功率运行区间可以直观反映换流站的可行功率运行范围。利用混合型MMC稳态模型解析地计算MMC在不同直流电压和功率运行点的各电气量和控制量的稳态值,将工程中考虑的各项约束条件转化为相应电气量与控制量的数学表达式,即可利用稳态模型定量分析计算考虑电气量和控制量的各项约束条件时换流站的功率运行区间,并定量分析各项约束条件及换流站参数对运行区间的影响。

3.1　子模块均压约束

文献[24]考虑的MMC运行约束条件包括交流调制比最大值和最小值约束、桥臂电流最大值约束、子模块电容电压波动范围约束、交流电流最大值约束和直流电流最大值约束,如下式所示:

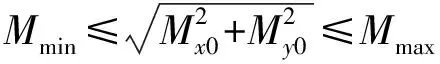
(14)

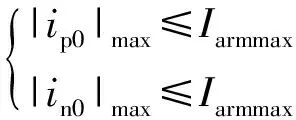
(15)

|Δuc0max|≤ΔUcmax

(16)

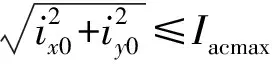
(17)

Idc≤Idcmax

(18)

混合型MMC相比半桥型MMC,其在运行中还需要额外考虑桥臂子模块的均压约束,即当桥臂有半桥子模块投入时,桥臂电流在一个周期内需要包含正、负两个方向以使得半桥子模块电容能够充放电,避免单向的桥臂电流使得投入的半桥子模块电容一直处于充电或放电状态,无法实现子模块的电容电压平衡。其中,桥臂电流的换向要求可以表示为:

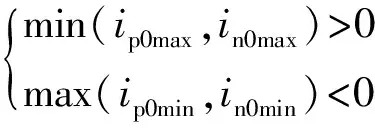
(19)

根据桥臂输出电压的大小可以判断是否需要投入半桥子模块。假设每个桥臂分别含有NFB个全桥子模块和NHB个半桥子模块(不考虑冗余),以上桥臂为例,结合式(3),可以得到上桥臂输出电压表达式为:

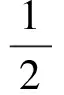
Mx20cos(2ωt)+My20sin(2ωt))·

(20)

当桥臂输出电压最大值upmax大于所有全桥子模块能够输出的最大电压,即满足式(21)时,需要投入半桥子模块。即

upmax>NFBucN

(21)

因此,当桥臂输出电压满足式(21)时,混合型 MMC桥臂电流需要满足换向要求式(19);反之,则不用考虑子模块均压约束。

3.2　功率运行区间计算

当直流电压确定时,混合型MMC的运行区间边界由各项运行约束条件刻画。由于混合型MMC可以运行在低直流电压下,因此其运行区间和运行特性还受直流电压的影响。在分析计算某一直流电压水平下混合型MMC 功率运行区间时,具体计算步骤如下。

步骤1:确定要考虑的直流电压运行水平Udc0。

步骤2:根据直流电流和换流器容量约束条件,初定待扫描的运行区域{(idc0,Q0) |-Idcmax≤idc0≤Idcmax,-Smax≤Q0≤Smax}。选取某一运行工况idc0,k+jQ0,k,利用所提出的稳态模型及求解方法,求解式(9)、式(12)和式(13)构成的非线性代数方程组,计算该工况下各个电气量与控制量的坐标轴分量稳态值,包括ix0,iy0,x8th0,Mx0,My0,Mx20,My20,Mdc0。

步骤3:将求解的结果代入式(14)至式(18),校核各电气量和控制量是否满足相应的约束条件;求解桥臂输出电压最大值,当其满足式(21)时,桥臂电流需要满足式(19)。

步骤4:当所有电气量和控制量满足前述各项约束条件时,计算该运行点下的P0,k+jQ0,k,记录该运行工况。以此类推,选择下一个运行点idc0,k+1+jQ0,k+1,其中,当无功功率未达到扫描区域边界时idc0,k+1=idc0,k,Q0,k+1=Q0,k+Qstep,Qstep为无功功率取值步长;当直流电流未达到扫描区域边界时,idc0,k+1=idc0,k+Idc,step,Q0,k+1=Q0,k,Idc,step为直流电流取值步长。返回步骤2继续校验该运行点是否满足所有运行约束条件。

上述计算步骤具体流程图如图3所示。通过扫描各种运行工况,可以计算得到Udc0直流电压下满足各项运行约束条件时混合型MMC的功率运行点的集合,构成其可行功率运行区间。改变Udc0值,可以计算功率运行区间在不同直流电压水平下的特性。

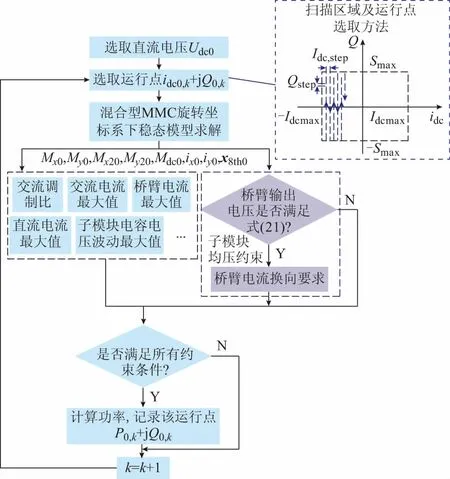
图3　计算功率运行区间流程图Fig.3　Flow chart for calculation of power operating zone

4　功率运行区间计算及参数影响分析

4.1　不同直流电压下运行区间

以附录B图B2所示测试系统为例,利用本文提出的混合型MMC稳态解析模型,计算该换流器在满足附录B表B2所示约束条件时不同直流电压下的功率运行区间,取各约束条件的交集,即得到功率运行特性图。表B2中考虑的约束条件包括桥臂电流最大允许值、直流线路电流最大允许值、换流器调制比运行范围、子模块电容电压波动最大允许值和换流器的传输容量约束。

首先,令直流电压从0.01以0.01为步长逐渐增大至0.5,直流电流的扫描范围是[-2,2],步长Idc,step=0.005,无功功率的扫描范围是[-1,1],步长Qstep=0.005,由此得到的功率运行区间和直流电压的三维视图及二维仰视图如附录B图B5所示。可以看到,随着直流电压的升高,功率运行区间的面积逐渐增大。同时,低直流电压下换流器传输的有功功率受限,而运行区间始终可以覆盖无功功率轴的[-1,1]范围,因此无功功率可以传输的最大值并不受直流电压影响。为了进一步分析功率运行区间边界的形成原因及各项约束条件对功率运行区间的刻画作用,下文分别取直流电压为0,0.1,0.2和0.5时的功率运行区间进行分析。选取扫描区域中满足某一运行约束条件的运行点集合,其边界即为该运行约束条件产生的功率运行区间的边界。

4.2　运行区间形成原因分析

图4(a)至(c)所示为直流电压分别为0,0.1和0.2时的可行功率运行区间。可以看到,其范围主要由子模块均压约束、子模块电压约束、直流电流约束和换流器容量约束决定。同时可以看到,功率运行区间关于有功功率P轴并不对称,当换流器吸收功率(Q>0)时,运行区间的面积更大。

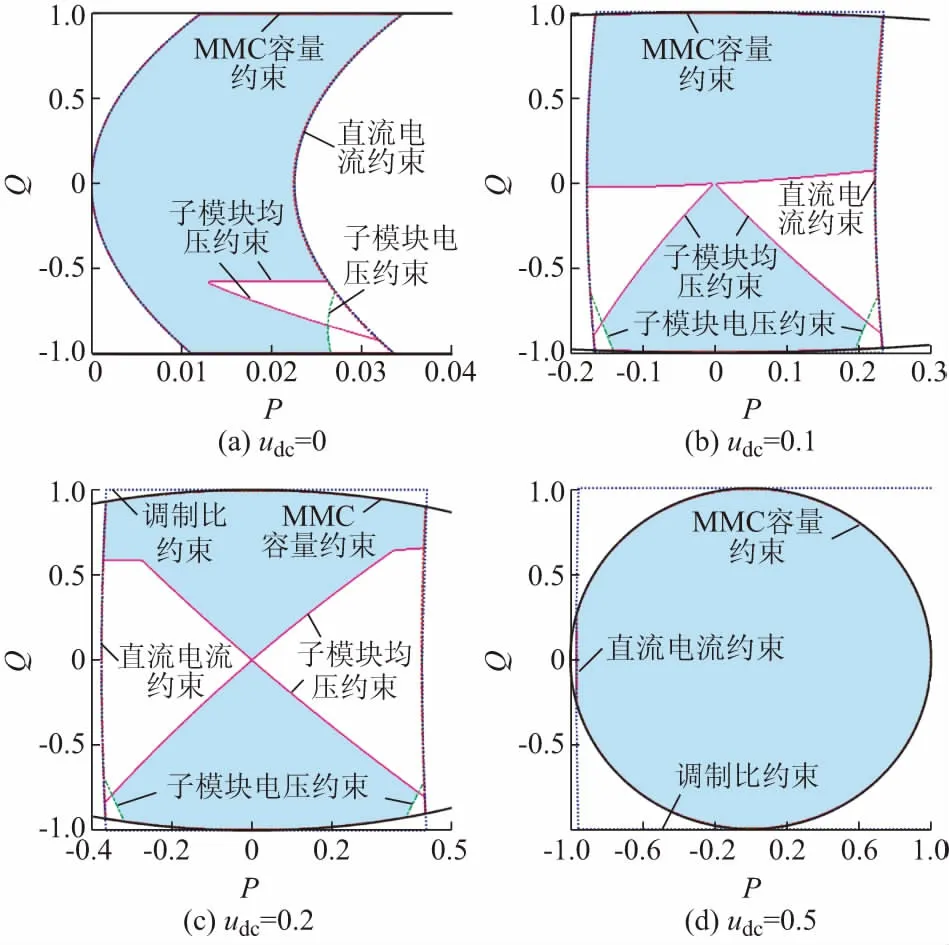
图4　不同直流电压下运行约束条件对功率运行区间影响分析Fig.4　Impact analysis of different operating constraints on operating zone under different DC voltages

为了解释运行区间不对称的原因,以上桥臂为例,忽略桥臂电抗器的压降,桥臂输出电压可以近似用换流器交流侧电流和直流电压表示为:

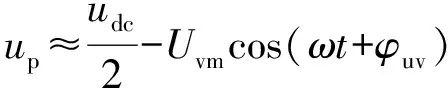
(22)

式中:Uvm和φuv分别为换流器交流侧相电压uv(t)的幅值和相位。

因此up的最大值可以近似为udc/2+Uvm。考虑到换流器传输的无功功率与其交流侧电压之间满足如下关系:

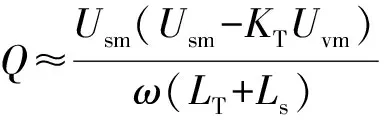
(23)

当换流器发出无功功率(Q<0)时,相比Q>0的情况,Uvm要大一些,因此桥臂输出电压的最大值要高一些,需要投入半桥子模块以产生足够的桥臂电压,故必须满足子模块均压约束。从而,运行区间边界受到子模块均压约束的限制,如图4(a)至(c)的下半部分所示。

而当Q>0时,在低直流电压下,桥臂输出电压最大值较小,因此可全部由全桥子模块产生,故无需考虑均压约束,如图4(a)和(b)上半部分所示。随着直流电压增大,如图4(c)上半部分所示,在低无功功率水平下,半桥子模块需要投入以产生足够的桥臂电压,此时桥臂中的无功电流需要保证桥臂电流同时含有正负成分以保证子模块正常均压。由于直流电流会加剧桥臂电流的直流偏置,影响子模块均压,因此直流电流反映的有功功率水平会受到子模块均压约束的限制,如图4(c)上半部分所示。随着吸收无功功率水平的增加,Uvm进一步降低,直到桥臂电压可以全部由全桥子模块产生,此时功率运行区间不再受子模块均压约束限制,如图4(c)顶部所示。

当直流电压进一步增大,如图4(d)所示,可以看到,此时运行区间仅受直流电流和换流器容量约束限制,换流器子模块均压约束不再是影响运行区间边界的主导约束之一。而根据式(22),此时桥臂电压最大值较大,半桥子模块会投入,但是通过计算可以发现此时桥臂电流自然满足换向条件,即同时包含正负分量。原因简述如下。

以上桥臂电流为例,考虑二倍频环流抑制作用效果时,其可以用交流电流和直流电流表示为:

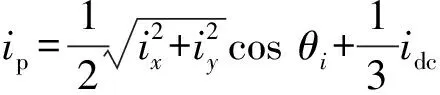
(24)

式中:θi为交流电流相位。

若忽略换流器损耗,根据交直流侧有功功率平衡,可以得到:

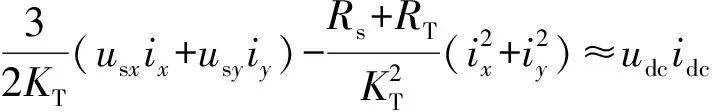
(25)

通常情况下,Rs与RT均较小,usx0=Usm,usy0=0,所以交流电流的坐标轴分量可以近似表示为:

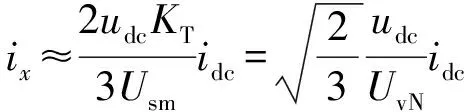
(26)

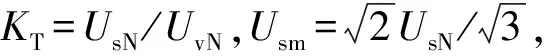
本算例中,根据附录A表A1所示参数,udc=0.5UdcN,UvN=0.55UdcN,代入式(26),可以得到:

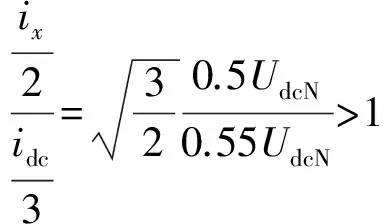
(27)

因此桥臂电流肯定包含正负分量,故子模块均压约束可以自然地满足。

4.3　参数对运行区间影响

本节主要研究桥臂电抗器Larm、子模块电容Csub和全桥子模块比例nFB对功率运行区间的影响。以直流电压udc=0.2为例,当上述三种参数分别变化时,功率运行区间变化情况如图5所示。

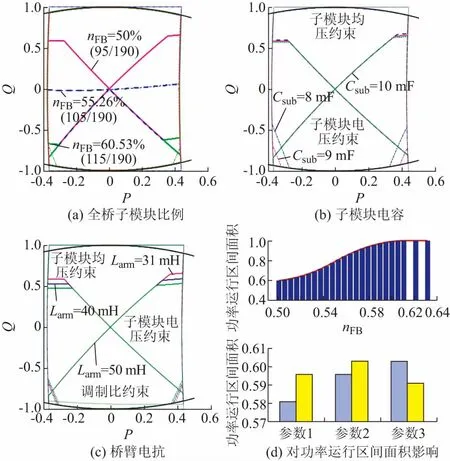
图5　参数对功率运行区间影响分析Fig.5　Impact of parameters on power operating zone

当全桥子模块比例从50%(95/190)增大到60.53%(115/190)时,运行区间的边界变化如图5(a)所示,可以看到,随着全桥子模块比例提高,子模块均压约束对运行区间边界的限制作用逐渐降低,运行区间面积大大增加。

当子模块电容分别取8,9,10 mF时,运行区间面积增大并不明显,如图5(b)所示。子模块电压约束对运行区间的限制作用随着子模块电容增加而减弱,针对本算例,当子模块电容取10 mF时,子模块电压约束不再对运行区间起限制作用。

当桥臂电抗器分别取31,40,50 mH时,如图5(c)上部分所示,子模块均压约束对运行区间的限制随着桥臂电抗器的增大而略微减弱,运行区间略微增加;而从图5(c)下半部分可以看到,当桥臂电抗器过大时,调制比约束会开始对运行区间产生限制作用,运行区间反而会缩小。子模块电压约束对运行区间的限制也会随着桥臂电抗器的增大而加强,导致运行区间略微缩小。

图5(d)定量总结了这三种参数(参数1:Csub=8 mF,Larm=31 mH;参数2:Csub=9 mF,Larm=40 mH;参数3:Csub=10 mF,Larm=50 mH)对运行区间面积的影响。其中,规定直流电流和换流器容量约束共同限制的功率运行区间面积为100%。可以看到,当全桥子模块比例达到61.05%(116/190)时,运行区间的面积达到“饱和”状态,不再随全桥子模块比例增加而增大。和全桥子模块比例相比,子模块电容与桥臂电抗器对运行区间的影响较小。

5　结论

1)本文提出了混合型MMC在旋转坐标系下的动态解析模型,该动态解析模型考虑了换流器内部电气动态,通过调制信号作为控制部分的接口,可以方便地与外部控制系统联合建模;以交流电流作为交流侧电气接口和直流电压作为直流侧电气接口,可以方便地与交流系统和直流网络联合建模。

2)基于动态解析模型,提出了混合型MMC稳态解析模型。利用稳态解析模型可以实现对混合型MMC运行特性在任意直流电压下的完全解析求解,给定直流电压水平和任意运行点(有功功率/直流电流,无功功率等)即可计算出混合型MMC的子模块总电容电压、桥臂电流等内部电气量和调制信号的稳态值,为解析地分析混合型MMC的参数设计和运行特性提供了理论支撑。

3)利用稳态解析模型研究混合型MMC在不同直流电压水平下满足多种运行约束条件时的功率运行区间,尤其要考虑半桥子模块的均压约束。低直流电压下,混合型MMC的运行区间并不对称,即发出无功功率的可行性比吸收无功功率的可行性更高,这主要受子模块均压约束的影响。当直流电压大于0.5时,换流器功率运行区间不再受子模块均压约束限制。

4)适当提高桥臂全桥子模块比例可以增大功率运行范围,但是全桥子模块比例存在饱和点(本文算例中是61%左右),继续增大全桥子模块比例并不会增大功率运行范围。同时,增大子模块电容与增大桥臂电抗器对于扩大功率运行范围作用并不明显。

5)本文利用所提解析模型主要研究了混合型 MMC稳态特性,未能展开对混合型MMC动态特性的研究,后续将针对其小信号模型及小信号稳定性开展深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 孔明,汤广福,贺之渊.子模块混合型MMC-HVDC直流故障穿越控制策略[J].中国电机工程学报,2014,34(30):5343-5351.

KONG Ming, TANG Guangfu, HE Zhiyuan. A DC fault ride-through strategy for cell-hybrid modular multilevel converter based HVDC transmission systems[J]. Proceedings of the CSEE, 2014, 34(30): 5343-5351.

[2] ZENG Rong, XU Lie, YAO Liangzhong, et al. Design and operation of a hybrid modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1137-1146.

[3] TANG Guangfu, HE Zhiyuan, PANG Hui. R&D and application of voltage sourced converter based high voltage direct current engineering technology in China[J]. Journal of Modern Power Systems and Clean Energy, 2014, 2(1): 1-15.

[4] YU Xinyu, WEI Yingdong, JIANG Qirong, et al. Neutral-point-clamped hybrid multilevel converter with DC fault blocking capability for medium-voltage DC transmission[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(4): 524-536.

[5] RODRIGUEZ P, ROUZBEHI K. Multi-terminal DC grids: challenges and prospects[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(4): 515-523.

[6] 徐政,薛英林,张哲任.大容量架空线柔性直流输电关键技术及前景展望[J].中国电机工程学报,2014,34(29):5051-5062.

XU Zheng, XUE Yinglin, ZHANG Zheren. VSC-HVDC technology suitable for bulk power overhead line transmission[J]. Proceedings of the CSEE, 2014, 34(29): 5051-5062.

[7] 吴亚楠,吕铮,贺之渊,等.基于架空线的直流电网保护方案研究[J].中国电机工程学报,2016,36(14):3726-3734.

WU Yanan, LÜ Zheng, HE Zhiyuan, et al. Study on the protection strategies of HVDC grid for overhead line application[J]. Proceedings of the CSEE, 2016, 36(14): 3726-3734.

[8] 向往,林卫星,文劲宇.自阻型模块化多电平换流器故障后恢复策略与等值模型[J].电力系统自动化,2017,41(5):84-92.DOI:10.7500/AEPS20160427001.

XIANG Wang, LIN Weixing, WEN Jinyu. Fast recovery strategy and equivalent electromagnetic model of self-blocking modular multilevel converters[J]. Automation of Electric Power Systems, 2017, 41(5): 84-92. DOI: 10.7500/AEPS20160427001.

[9] LIN Weixing, JOVCIC D, NGUEFEU S, et al. Full bridge MMC converter optimal design to HVDC operational requirements[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1342-1350.

[10] ZENG Rong, XU Lie, YAO Liangzhong, et al. Precharging and DC fault ride-through of hybrid MMC-based HVDC systems[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1298-1306.

[11] CUI Shenghui, SUL S K. A comprehensive DC short-circuit fault ride through strategy of hybrid modular multilevel converters (MMCs) for overhead line transmission[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7780-7796.

[12] HU Jiabing, XU Kecheng, LIN Lei, et al. Analysis and enhanced control of hybrid-MMC-based HVDC systems during asymmetrical DC voltage faults[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1394-1403.

[13] XIANG Wang, LIN Weixing, XU Lie, et al. Enhanced independent pole control of hybrid MMC-HVDC system[J/OL]. IEEE Transactions on Power Delivery[2017-06-13]. DOI: 10.1109/TPWRD.2017.2715040.

[14] 李少华,王秀丽,李泰,等.混合式MMC及其直流故障穿越策略优化[J].中国电机工程学报,2016,36(7):1849-1858.

LI Shaohua, WANG Xiuli, LI Tai, et al. Optimal design for hybrid MMC and its DC fault ride-through strategy[J]. Proceedings of the CSEE, 2016, 36(7): 1849-1858.

[15] 李红梅,行登江,高扬,等.子模块混联MMC-HVDC系统直流侧短路故障电流抑制方法[J].电力系统保护与控制,2016,44(20):57-64.

LI Hongmei, XING Dengjiang, GAO Yang, et al. A DC pole-to-pole fault current suppression strategy of the half-and full-bridge based cell-hybrid modular multilevel converter[J]. Power System Protection and Control, 2016, 44(20): 57-64.

[16] 魏承志,练睿,杨桦,等.一种混合型模块化多电平换流器的改进载波移相调制方法[J].电力系统自动化,2016,40(7):68-73.DOI:10.7500/AEPS20150701002.

WEI Chengzhi, LIAN Rui, YANG Hua, et al. An improved phase shifted carrier modulating method for hybrid modular multilevel converter[J]. Automation of Electric Power Systems, 2016, 40(7): 68-73. DOI: 10.7500/AEPS20150701002.

[17] 王姗姗,周孝信,汤广福,等.模块化多电平电压源换流器的数学模型[J].中国电机工程学报,2011,31(24):1-8.

WANG Shanshan, ZHOU Xiaoxin, TANG Guangfu, et al. Modeling of modular multi-level voltage source converter[J]. Proceedings of the CSEE, 2011, 31(24): 1-8.

[18] 宋强,刘文华,李笑倩,等.模块化多电平换流器稳态运行特性的解析分析[J].电网技术,2012,36(11):198-204.

SONG Qiang, LIU Wenhua, LI Xiaoqian, et al. An analytical method for analysis on steady-state operating characteristic of modular multilevel converter[J]. Power System Technology, 2012, 36(11): 198-204.

[19] SONG Qiang, LIU Wenhua, LI Xiaoqian, et al. A steady-state analysis method for a modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3702-3713.

[20] 肖晃庆,徐政,薛英林,等.模块化多电平换流器谐波特性解析分析[J].中国科学:技术科学,2013,43(11):1272-1280.

XIAO Huangqing, XU Zheng, XUE Yinglin, et al. Theoretical analysis of the harmonic characteristics of modular multilevel converters[J]. Science China: Technological Sciences, 2013, 43(11): 1272-1280.

[21] 刘普,王跃,雷万钧,等.模块化多电平变流器稳态运行特性分析[J].电工技术学报,2015,30(11):90-99.

LIU Pu, WANG Yue, LEI Wanjun, et al. Analysis of steady-state operating characteristics for modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 90-99.

[22] 彭浩,邓焰,王莹,等.模块化多电平变换器模型及稳态特性研究[J].电工技术学报,2015,30(12):120-127.

PENG Hao, DENG Yan, WANG Ying, et al. Research about the model and steady-state performance for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 120-127.

[23] JOVCIC D, FAR J. Phasor model of modular multilevel converter with circulating current suppression control[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1889-1897.

[24] 鲁晓军,林卫星,安婷,等.MMC电气系统动态相量模型统一建模方法及运行特性分析[J].中国电机工程学报,2016,36(20):5489-5501.

LU Xiaojun, LIN Weixing, AN Ting, et al. A unified dynamic phasor modeling and operating characteristic analysis of electrical system of MMC[J]. Proceedings of the CSEE, 2016, 36(20): 5489-5501.

[25] XIANG Wang, LIN Weixing, AN Ting, et al. Equivalent electromagnetic transient simulation model and fast recovery control of overhead VSC-HVDC based on SB-MMC[J]. IEEE Transactions on Power Delivery, 2017, 32(2): 778-788.

[26] 周诗嘉,林卫星,姚良忠,等.两电平VSC与MMC通用型平均值仿真模型[J].电力系统自动化,2015,39(12):138-145.DOI:10.7500/AEPS20140615001.

ZHOU Shijia, LIN Weixing, YAO Liangzhong, et al. General averaged value models for two-level VSC and MMC[J]. Automation of Electric Power Systems, 2015, 39(12): 138-145. DOI: 10.7500/AEPS20140615001.

鲁晓军(1990—),男,博士研究生,主要研究方向:柔性直流换流器建模和直流电网稳定性分析等。E-mail： luxiaojun@hust.edu.cn

向往(1990—),男,通信作者,博士,主要研究方向:模块化多电平换流器、直流电网运行与控制。E-mail: xiangwang1003@foxmail.com

林卫星(1986—),男,博士,主要研究方向:直流电网、直流-直流变换器、直流输电等。E-mail: weixinglin@foxmail.com