基于信号流图法对单自由度行星轮系功率特性的研究

周新涛, 崔亚辉, 刘　凯

(西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)

在所有的机械传动中,行星轮传动以外形尺寸小和质量轻、承载能力与传动效率高等特点在各个领域中得到了广泛应用,如无级变速器等[1]。行星轮机构在实际应用中,由于影响传动功率的因素很多,而且这些因素目前尚处在研究阶段。为了找出对传动效果不利的因素,一些研究者从行星轮系的运动特性和传动特性等方面入手研究,也取得了很多显著的研究成果[2-5]。但随着科学技术水平的发展,许多应用领域对机构传动水平的要求也不断地提高,如高速稳定、高精度和大功率,以及无级变速等方面的应用。这就导致了使行星轮传动系统的结构更加复杂,且影响传动功率的不明因素增多,故此时若采用传统的分析方法来研究复杂行星轮系的功率特性时,就难以取得理想的效果。

本文采用一种新的计算方法—信号流图法的基本理论研究复杂行星轮系的功率特性,能避免上述计算中存在的问题。目前,已有部分学者将信号流图法的基本理论应用到机械传动的研究中,并获得了一些研究成果。如林建德[6]应用图论的方法,以实现汽车自动变速机构的运动构造设计中,得出了一套简易且系统化的设计程序。杨亚联等[7]建立了混合动力汽车行星耦合传动系统的图论模型,并通过这种方式对单、双排行星耦合机构传动系统进行运动学与动力学分析,为行星耦合传动系统的选型提供了一种新方案。张伟社等[8]将行星变速器、离合器和制动器的结构,分别构造出对应的信号流流图模型,并用信号流图理论计算法算出它们的角速度、转矩和功率流等方面的特性参数。杨兴海等[9-10]利用信号流图法的简化规则将复式轮系基本结构的流程图模型建立起来,并给出了常用周转轮系信号流图的构建步骤及运动学分析结果。虽然利用信号流图法研究复杂行星轮系的功率特性,尚未形成完整的理论体系,但能为复杂行星齿轮传动功率特性参数计算提供一种全新的途径。另外,该法直观性较好、计算效率高,且能够明确的表明复杂行星齿轮传动特性的机理。

1　行星轮系的传动结构

针对行星轮系所特有的传动特征,在各个领域的实际应用中,可以灵活地将基本行星轮系进行串联、并联和混联等方式组合,能获得不同传动特性的行星系统。本文中将给出五种最典型、最基本的行星轮混联系统,并用来研究其系统的功率特性。

1.1　单环路行星轮系

根据行星轮系组合方式的不同,可以将单环路行星轮系分为:XP型混联系统和PX型混联系统。在这两种混联系统中,均有一个行星轮系X与一个基本轮系P组成。其结构如图1中的图(a)和图(b)所示,图中的字母a、b、c、α、β均为传动构件、I为输入轴,O为输出轴,Ji(i=0,1)为中间节点。

图1　单环路行星轮系的结构简图Fig.1　Simple structural graph of single-loop planetary gear system

1.2　双环路行星轮系

为了合理地对复杂行星轮系进行综合分析,必须具备从这些结构中选择最佳结构图的总体简图。这样的总体简图消除了选择简图时的偶然性因素,并允许在最后阶段正确地解决设计中存在的问题。根据复杂行星轮系简图的构成规则及总体简图的选择原则,本部分给出了三种较为典型的T型、Π型和E型混联系统的总体简图,见图2。其中,X为行星轮系组,P为基本轮系组,Ji(i=0～4)为中间节点。

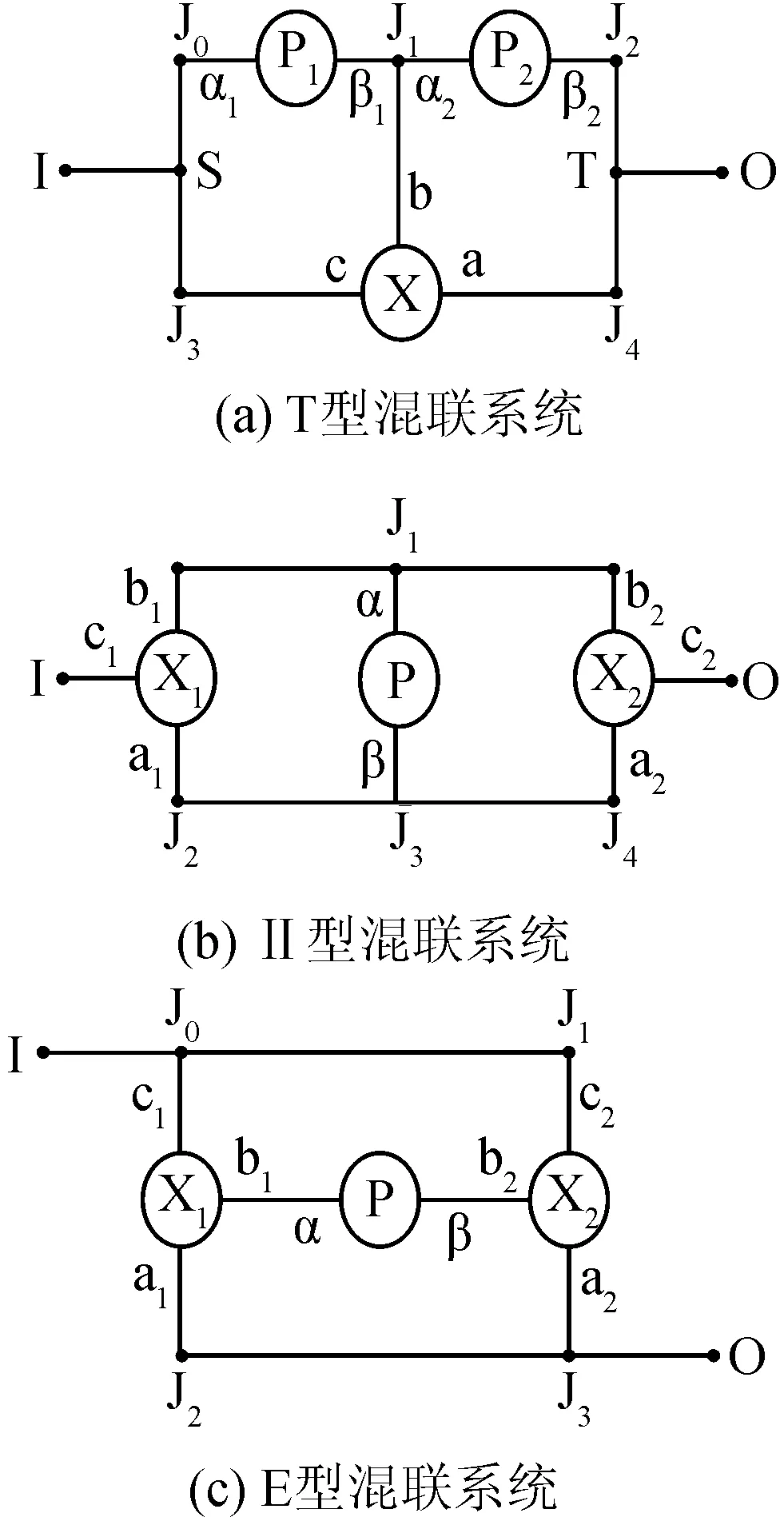
图2　双环路行星轮系的结构简图Fig.2　Simple structural graph of double-loop planetary gear system

2　建立信号流图模型

2.1　建模规则

1) 将行星轮系中的齿轮、系杆等构件,简化成信号流图中的节点。输入端的构件简化成源节点,输出端的构件简化成汇节点(目标节点)。

2) 按照行星轮系传动链间运动传递的关系,将各个节点用带有方向的弧线连接起来。

3) 将各个轮系传动链间的传动参数,以权值(增益)的形式给出,并合理地赋值给对应的有向弧线。

4) 在信号流图模型的构建过程中,根据需要可以在各个前向通路上设置权值为单位1的中间节点。

5) 按照信号流图的简化计算方法,将各拓扑图进行简化,并求出各类型轮系传动的计算关系式。

2.2　建立拓扑图模型

依据行星轮系传动链的传动特性,并结合信号流图中流的传递机理。本节在无封闭功率流的情况下,建立起XP型、PX型、T型、Π型和E型混联系统的信号流图模型。

1) 单环路行星轮系

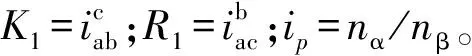
2) 双环路行星轮系

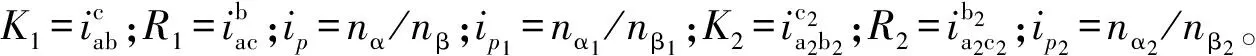
图3　单环路行星轮系的信号流图模型Fig.3　Signal flow model of single-loop planetary gear system

2.3　行星轮系的特性参数计算

按照图3～4所示给出的信号流图模型,再结合信号流图的简化计算原理,将各种类型的混联轮系进行简化计算。其逐步简化过程较为繁琐,且计算量较大。故在本节处不再作出更多的说明,仅给出各种混联系统的计算结果,其结果包括混联系统输入与输出端的转速、转矩等特性参数计算关系式,见表1。

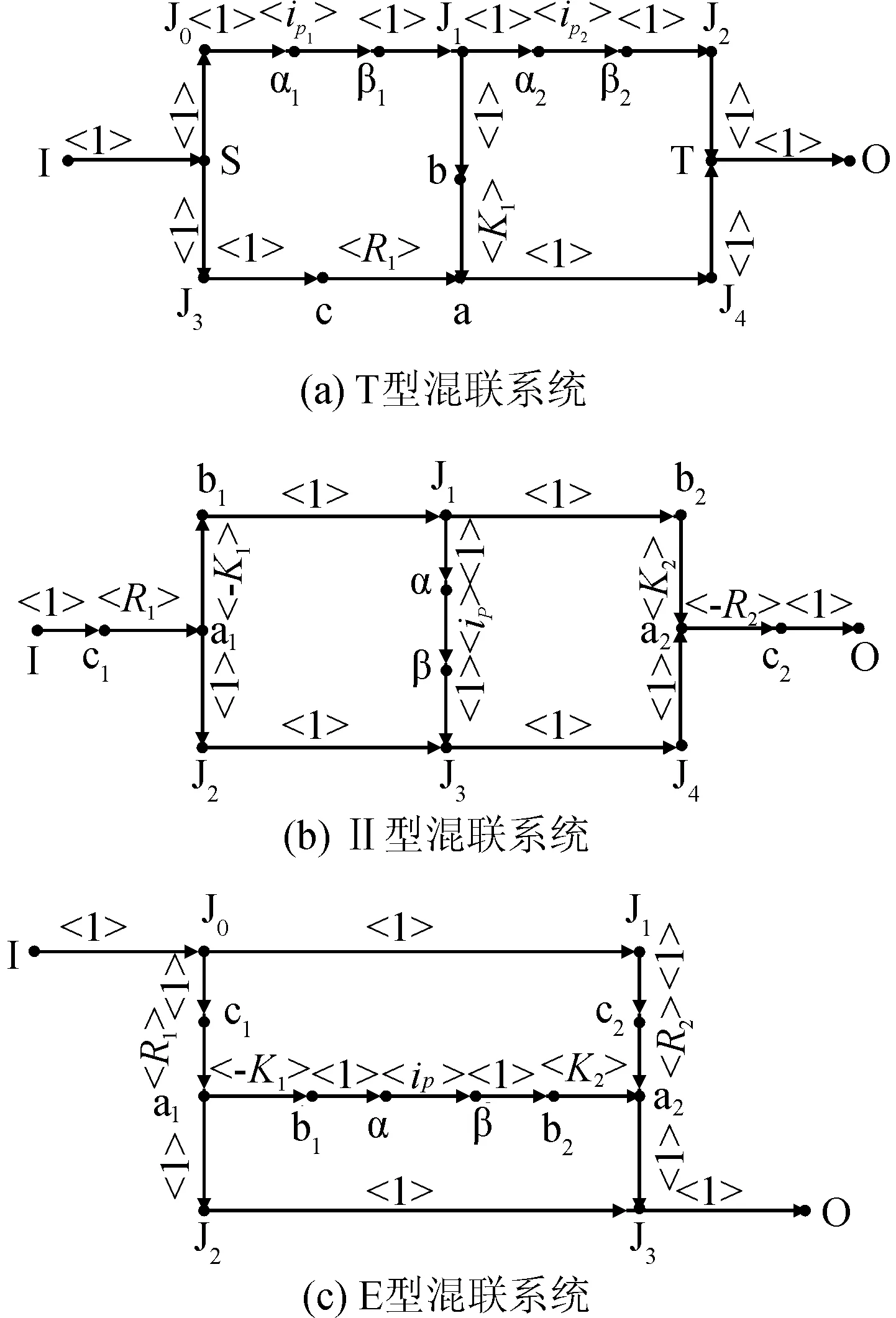
图4　双环路行星轮系的信号流图模型Fig.4　Signal flow model of double-loop planetary gear system

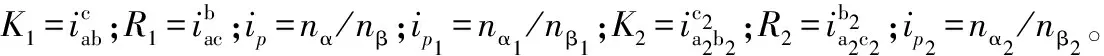
3　行星轮系的功率特性计算

针对行星轮系传动系统的结构特征,采用式(1)计算出行星轮系的功率特性参数。该式中的转速n与转矩T,可以通过表1中各种混联系统的计算结果查取即可。

(1)

式中:n为转速(r/min);T为转矩(N·m)。

在不计摩擦等损失的情况下,本节处将给出XP型、PX型、T型、Π型和E型混联系统,输入、输出轴之间总功率P的计算关系式。

3.1　单环路行星轮系的功率特性计算

1) XP型混联系统功率的计算结果

依据信号流图的计算规则,可以得出XP型混联系统输入、输出端功率的计算关系式:

(2)

式中:PI为输入端的功率;PO为输出端的功率;其它符号表示的含义同上。

2) PX型混联系统功率的计算结果

同理,可以得出PX型混联系统输入、输出端功率的计算关系式:

(3)

式中各符号表示的含义同上。

3.2　双环路行星轮系的功率特性计算

1) T型混联系统功率的计算结果

同理,可以得出T型混联系统输入、输出端功率的计算关系式:

(4)

式中各符号表示的含义同上。

2) Π型混联系统功率的计算结果

同理,可以得出Π型混联系统输入、输出端功率的计算关系式:

(5)

式中各符号表示的含义同上。

3) E型混联系统功率的计算结果

同理,可以得出E型混联系统输入、输出端功率的计算关系式:

(6)

式中:各符号表示的含义同上。

4　实例验证

图5是某型机械内运动系统的传动简图,在该传动系统中各齿轮的齿数分别为:Z1=24,Z2=48,Z3=30,Z4=90,Z5=100,Z6=40,Z7=20,且n1=1 450 r/min。若电机的输入转矩为TI=1 200 N·m,在不考虑其它形式的损耗情况下,试求输出轴O端的功率是多少?

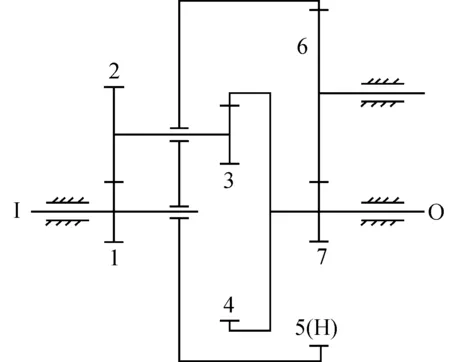
图5　结构的传动简图Fig.5　Transmission graph of the structure

分析:图5所示的结构图中以轮1为原动件时,该机构有两条传动路径:一路的路径由轮1-2-3-4组成;一路的路径是由差动轮系的系杆H来输出功率,即轮1-2-5-6-7组成。依据传动结构,可以得出该种结构为XP型混联系统。

根据本文中的简化方式建立传动机构的信号流图模型,其行星轮系的转速与转矩等参数按照表1中序号1的计算关系式求出。再按照式(2)计算输出轴的功率PO。

解:

1) 求解该机构输出轴的转速nO:

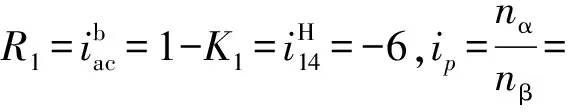
nO=nI×R1×(1-K1ip)-1=-1 933 (r/min)

2) 求解该机构输出轴的转矩TO:

3) 求解该机构输出轴的功率PO:

5　结　论

1) 将信号流图法的基本理论,引入到复杂行星轮系传动功率特性研究中。利用该法本文建立了XP型、PX型、T型、Π型和E型混联系统的信号流图模型。

2) 结合信号流图法的简化计算原理,首先得出这五种混联系统的转速和转矩等特性参数的计算关系式。

3) 再利用行星轮系传动功率的传统计算法,得到这五种混联系统的输入和输出端总体功率特性参数的计算关系式。

4) 应用信号流图法通过对行星轮系传动经典机构的功率参数计算,进一步验证该法在复杂行星轮系传动特性参数计算方面准确性与可行性。

参考文献:

[1] 刘晓琳, 崔亚辉. 车用功率分流无级变速驱动系统特性分析 [J]. 西安理工大学学报, 2007, 23(4): 406 -409.

LIU Xiaolin, CUI Yahui. The characteristic analysis of power split continuously variable transmission driving system for vehicle application [J]. Journal of Xi’an University of Technology, 2007, 23(4): 406-409.

[2] 崔亚辉, 马朝锋, 刘晓琳, 等. 封闭式行星传动的动力学分析 [J]. 中国机械工程, 2006, 17(增刊1): 62-63.

CUI Yahui, MA Chaofeng, LIU Xiaolin, et al. Dynamic analysis of encased differential gear train [J]. China Mechanical Engineering, 2006, 17(S1): 62-63.

[3] HSIEH H, TSAI L. Kinematic analysis of epicyclic-type transmission mechanisms using the concept of fundamental gearde entities [J]. Journal of Mechanical Design, 1996, 118(2): 294-299.

[4] CHEN Chao, ANGELES J. Virtual-power flow and mechanical gear-mesh power losses of epicyclic gear trains [J]. Journal of Mechanical Design, 2007, 129(1): 107-113.

[5] 王振, 崔亚辉, 刘凯, 等. 装备单环路系统的整车行驶动力学研究 [J]. 中国机械工程, 2016, 27(8): 1123-1129.

WANG Zhen, CUI Yahui, LIU Kai, et al. Research on driving dynamics for vehicles equipped with a single loop systems [J]. China Mechanical Engineering, 2016, 27(8): 1123-1129.

[6] 林建德. 一种汽车自动变速机构的运动构造设计方法 [J]. 机械科学与技术, 2006, 25(9): 1076-1081.

LIN Jiande. A design methodology for the kinematic structure of planetary gear trains for automatic transmissions [J]. Mechanical Science and Techinology, 2006, 25(9): 1076-1081.

[7] 杨亚联, 米娇, 胡晓松, 等. 混合动力汽车行星耦合传动系统的图论建模及动力学分析 [J]. 汽车工程, 2015, 37(1): 9-15.

YANG Yalian, MI Jiao, HU Xiaosong, et al. Graph theory modeling and dynamics analysis on the coupled planetary transmission system of HEV [J]. Automotive Engineering, 2015, 37(1): 9-15.

[8] 张伟社, 杨小安. 行星变速箱特性参数信号流图分析法 [J]. 机械设计与研究, 1997，(1): 20-22.

[9] 黄林. 信号流图的扩展及其应用 [J]. 东南大学学报, 1998, 28(4): 44-48.

HUANG Lin. Expanding of signal flow graphs and its application [J]. Journal of Southeast University, 1998, 28(4): 44-48.

[10] 杨兴海. 轮系运动分析的新方法——信号流程图法 [J]. 机械传动, 1995, 19(3): 5-8.

YANG Xinghai. New method for kinematic analysis of gear trains-Signal flow chart method [J]. Journal of Mechanical Transmission, 1995, 19(3): 5-8.