样本发散型含糊类的形式刻画*,†

周北海

北京大学哲学系zhoubh@phil.pku.edu.cn

张立英

中央财经大学现代逻辑研究所clearliying@126.com

1 导言

含糊性（vagueness）是常见的语言现象。对此早在古希腊时代就提出了秃头悖论。今天是逻辑学、语言学等多个学科关注的热点问题。含糊性研究主要处理含糊表达如高、矮、贵、秃等的语义解释、边界例子的真值以及其所带来的累积悖论等一系列问题。从1970年代前后起，关于含糊性的理论逐渐丰富起来，出现了模糊逻辑方向（[9,5]等）、超赋值理论（[2]等）、三值逻辑方向（[7]等）、认知主义方案（[6,8]等）、以及情境主义（[4,3]等）、容忍度理论（[1]）等研究分支。与以往研究有所不同，[10]从认知的角度提出了含糊类（vague class）的概念，并据此在一阶扩张语言中给出了刻画含糊类的形式语言和形式语义，以及以此为基础给出了秃头悖论的一个消解方案。其中所提出的含糊的理论有两个初始要素：样本和不可分辨性。通过样本和认知主体关于样本的不可分辨性，形象地看，可以得到一些以样本为中心的团（集合）。再取所有团的并，于是得到了一个类，即含糊类。对此可以取所有团的交得到含糊类的核。通过含糊类与其核的关系，还可以定义个体属于某含糊类的含糊度以及整个含糊类的含糊度。含糊类可以通过样本和不可分辨性（或相似性）确定含糊类的边界，从而使得秃头悖论中的归纳法推理有了上界，达到对这个悖论的消解。

上述含糊类及其相应理论的提出主要是基于来自于秃头这样的含糊类的直观。秃头这种含糊类有两个特点：(1)从n根头发到n+1根头发，一般看不出区别，这就是不可分辨性的来源。但是用在其他一些种类的含糊类上，比如个子，有时我们能够看出两个人身高有些差别，但是还是愿意将他们算作同类身高的人。这表明，在确定含糊类的过程中，不可分辨性过于严格。对此，可以用相似性来代替不可分辨性，从而使得含糊类的确定方法可以用于更广泛的领域。1这个建议来自于王文方教授。在本文余下的论述中都将使用“相似性”。以某样本和所有与之相似的个体形成的类称为由该样本得到的相似类。(2)秃头会有一个底线，0根头发。任何可以作为样本的秃头，都不会与0根头发相距“太远”。更好的例子还有中等个子、圆脸等。形象地看，确定这些类的样本会围绕某个中心进行，所以是收敛的。这样的含糊类可以称为样本收敛型含糊类。但是对于高个、长脸这样的含糊类来说，没有这个收敛的点。从普通的高个，比如用1.9米的某个高个A先生做样本，到以姚明那样的高个做样本，中间有很大差距。而且还可以有更高的高个做样本，上不封顶。形象地看，高个的样本是发散的。这样的含糊类可以称为样本发散型含糊类。样本发散带来的结果之一是导致了无核含糊类。

我们在之前的理论（[10]）中注意到了无核含糊类，但是所给出的主要还是关于有核含糊类的理论。对于无核含糊类或样本发散型的含糊类来说，这个理论中的一些定义并不适用。所以，如何刻画无核含糊类还需要新的理论。本文主要是以无核含糊类为原型，对于这样的含糊类给出形式理论。

2 样本发散型含糊类

基于样本和相似性得到的含糊类大致可以陈述如下：设S是任意样本集。对任意的a属于S，令[a]是与a相似的个体形成的相似类（称为团）。于是有{[a]|a∈S}，即由S的样本形成的团的集合。令A=∪{[a]|a∈S}。A就是由S样本形成的含糊类。对此还可以有∩{[a]|a∈S}，这是与所有样本都相似的个体的集合，即A的核。如果∩{[a]|a∈S}∅，则A是有核含糊类，否则，是无核含糊类。从样本的角度看，所有样本有共同的相似个体，是样本收敛的含糊类，否则，是样本发散的含糊类。

样本发散含糊类的原型是高个、胖子等这样的含糊类。其特点是，样本之间可以有很大差异，从普通的高个到超级高个，甚至超超级高个，都可以是高个。这些高个之间可以有相当大的差异，因此不存在对于所有高个样本都相似的个体。

从直观上看，一个个体是否属于含糊类A有三种情况：(a)确定地是A；(b)确定地是非A（不是A）；(c)含糊地是A。情况(1)和(2)是两极情况，(3)是中间情况（即通常所说的边界情况）。对于有核含糊类来说，只需有A的全体和A的核就可以通过含糊类与核之间的差来定义中间情况。无核含糊类因为核为空所以无法通过这种方法定义中间情况。样本和相似性是基于认知的概念，通过样本和与样本的相似性是人们在认知含糊类时常用的方法，所以对于这个问题还是应该在样本和相似性的基础上加以解决。

解决的办法之一，是引入负样本，并且将原来的样本称为正样本，通过正样本和负样本共同作用，给出一个个体a是否属于某含糊类A的三种情况的刻画。这里的正样本是确定为A的一些个体，负样本是确定为非A的一些个体。例如，对于高个来说，可以选择一些我们确定是高个的人作为样本。相应地，关于高个的负样本，是那些在确定是非高个的人中选取的样本。引入负样本的根据是，在实际的认知过程中，人们通常会通过正反两个方面的对比来决定某个体是否属于某个类。2作为理论讨论，此时预设样本是充足的，即对于同一主题下的任意个体，总有正样本或样本与之相似。

引入负样本之后，关于个体a是否属于含糊类A的三种情况可以理解为：对于a来说，如果有关于A的正样本与之相似，并且没有负样本与之相似，那么a确定地是A。如果有关于A的负样本与之相似，并且没有正样本与之相似，那么a确定地是非A。在此二者之间，如果有正样本与之相似，且也有负样本与之相似，那么a既不确定地是A，也不确定地是非A，这时a就是含糊地是A。

例如，设A是高个这个含糊类，a是某个人。对上述三种情况有：如果有高个的样本与a相似且a不与任何非高个的样本相似，那么a确定地是高个；如果有非高个的样本与a相似且a不与任何高个的样本相似，那么a确定地是非高个；如果既有某个高个的样本与a相似，又有某个非高个的样本与之相似，那么a是既不确定是高个也不确定是非高个，即a含糊地是高个。

通过负样本的引入，可以给出(a)、(b)、(c)三种情况的严格表达，并且可以在此基础上再定义有核含糊类和无核含糊类：设A=∪{[a]|a∈S}，A是一个以S为样本集得到的含糊类。A是有核含糊类，当且仅当，A的核∩{[a]|a∈S}̸。这表明通过负样本的引入，可以得到更一般的含糊类定义。

负样本的引入涉及到含糊类的补，如上面所说的“非A”。在语言表达上，负样本涉及到负词项。传统逻辑通过“负概念”来讨论与此相关的问题。传统逻辑认为，负概念总是相对于一个特定的范围的（[11]，第31–32页）。例如，“非高个”所相对的范围是人，“非红”所相对的范围是颜色，“非机动车”所相对的范围是车辆。传统逻辑的理论在这里仍然适用，但是术语可以换成负词项，或负谓词。因为负谓词的引入，原来相应的谓词，如“高个”等，可以称为正谓词。

这里需要对范围做些特别说明。如果只是正谓词，范围的问题并不明显。但是如果还出现负谓词，那么这个范围的作用就会显现出来。例如，我们可以说“电脑不是机动车”，但是不能说，“电脑是非机动车”。这就是因为有车辆这个范围在起作用。这个范围以后称为关于负谓词的论域。负谓词都有相应的论域，如“非机动车”的论域是车辆，“非高个”的论域是人，如此等等。负谓词带有论域也可以说负谓词是带有论题的，因此这个范围以下也称为论题域，表达论题域的语词称为论题词，如上例中的“人”，“颜色”和“车辆”。

负谓词的论题域同时也是正谓词的论题域。与“非机动车”相应的正谓词是“机动车”。车辆既是“非机动车”的论题域，也是“机动车”的论题域。在这个论题域中，机动车和非机动车形成矛盾关系（不可同真，不可同假）。就一般的论域来说，此二者是反对关系（可以同假，不可同真）。这也表明，“x不是P”和“x是非P”在一些情况下并不等值。一般地，从“x是非P”可以得出“x不是P”，但是反过来并不总是成立的，从“x不是P”不一定能得出“x是非P”。“x不是P”（即“并非x是P”）是对“x是P”的否定，其中的“不”是命题联结词。“x是非P”中的“非”是对谓词P的否定，得到的是负谓词。

表达含糊类的谓词称为含糊谓词。形象地看，含糊类是边界不清晰的类，即存在一个模糊地带，其中的个体既不确定地是A，也不确定地是非A。设A是任意的类，以下用～A表示A的补，(A,～A)表示A和非A的含糊地带。于是，A是含糊类，当且仅当，(A,～A)∅。反之，如果(A,～A)=∅，则A称为清晰类（如偶数就是清晰类，因为偶数和非偶数之间不存在含糊地带）。关于含糊类直观上还应该有下面的命题：

设A是一个类，P是表达A的谓词，P～是相应的负谓词。此时P～表达的是A的补～A。如果A是含糊类，那么P就是含糊谓词。根据(a)，因为A是含糊类，所以～A也是含糊类，因此P～是含糊谓词。如果还有表达(A,～A)的谓词X，根据(b)，(A,～A)也是含糊类，所以X也是含糊谓词。X是正谓词和负谓词之间的谓词，可以称为中间谓词。

因为负样本的引入，在语言表达方面引入了负谓词，因此也有了正谓词，还有了中间谓词和论题词。这些都是在形式刻画时需要考虑的词类。以下将在一阶语言的基础上通过语言扩张的方法，增加一些要素，给出含糊类的形式刻画。

3 形式语言L∗和语义

L∗可以是任意一阶语言的扩张。先给出一阶语言L。

语言L

符号：L的初始符号有可数多个个体变元、常项符号和谓词符号，有联结词¬、→，量词符号∀，以及辅助符号(、)。被定义的符号有∧、∨、↔、∃，按通常定义。所有个体变元的集合记作V，常项符号集记作C，谓词符号集记作P。

词：(1)个体词：个体变项和个体常项都是个体词，分别用x,y,z和a,b,c等表示。个体词又称为项，用t（或加上下标）表示；

(2)谓词：任意谓词符号都是一个谓词，用P、Q等表示。

公式：φ ∶=t1≡ tn|Pt1···tn|¬φ |φ → ψ |∀xφ

语言L∗L∗是L的扩张，列出增加部分。

符号：设Π是任意指标集。对任意的P∈Π，有下列符号

词：对任意的P∈Π，～～P称为以P为论题的相似性等词，和DP是一元谓词，分别称为正、负样本谓词和论题词。

公式

可以看出，L公式都是L∗公式，L∗是L的扩张。L和L∗公式集分别记作F(L)和 F(L∗)。

L∗语义的结构和模型

L∗语义是L语义的扩张。L语义即标准的一阶语义，由结构A=〈D,η〉、指派ρ（对变元的赋值）、解释σ= 〈A,ρ〉等这几部分组成（参见[12]）。L公式t1=tn、Pt1···tn、¬φ、φ→φ以及∀xφ的解释按通常定义。解释也称为模型。

L∗中增加了表示含糊谓词的指标集Π，以及对任意的P∈Π，有相似性等词P，和新的谓词及相应的公式。下面考虑对于这几种语言表达式的解释。这需要对于原来的语义增加新的要素。

定义3.1(L∗结构) 一个L∗结构是一个L结构的扩张，记作A∗=〈D,T,δ,θ,ξ,{≈τ|τ∈ T},η∗〉，其中

(1)D是任意非空集，称为个体域；

(3)δ是T到℘(D)的映射（对任意的τ∈T，δ(τ)⊆D，即δ对任意的主题τ指定一个论题域）；

(4)θ是样本选择函数，对每个主题τ，选择一个正样本集θ+(τ)和一个负样本集 θ−(τ)，满足条件：θ+(τ)∪ θ−(τ)⊆ δτ，θ+(τ)∩ θ−(τ)= ∅；

(5)ξ∶Π →T（对任意的P∈Π，ξ(P)=τ∈T，即ξ将指标P解释为主题τ，也可以理解为，对每个谓词都赋予一个主题）；

(6)对任意的τ∈T，≈τ是δ(τ)上的自返、对称关系，满足条件：如果d∈δ(τ)且d ≈τd′则 d′∈ δ(τ)（δ(τ)对相似性封闭）；不存在 d ∈ θ+(τ)且 d′∈ θ−(τ)，使得d≈τd′（正样本和负样本之间没有≈τ关系）。

(7)η∗是η的扩张。对任意的L常项和谓词X，η∗的解释与η的解释相同，即

η∗(X)=η(X)。对于L∗增加的谓词的解释为

定义3.2(L∗模型) 设A∗= 〈D,η,T,δ,θ,ξ,{≈τ|τ∈ T}〉是任一L∗结构，ρ是对于变元的指派（按L语义对于指派的定义）。一个L∗的解释也称为一个L∗模型，记做 σ = 〈A∗,ρ〉，或 σ = 〈D,T,δ,θ,ξ,{≈τ|τ∈ T},η∗,ρ〉。

约定tσ=η∗(t)，如果t是常项；tσ=ρ(t)，如果t是变项。

定义3.3(L∗公式的赋值定义) 设σ是任意模型。

(1) σ(DPt)=1，当且仅当，tσ∈ η∗(DP)；

(3) σ(t ～～Pt′)=1，当且仅当，〈tσ,t′σ〉∈ η∗(～～P)（又记作 tσ≈ξ(P)t′σ）；

(4)如果φ是形如t1≡tn、Pt1···tn、¬φ、φ→ψ或∀xφ的公式，则σ(φ)按L语义的赋值定义。

定义3.4(真和有效) 设σ是任意L∗模型，φ是任意L∗公式。φ在σ中是真的，当且仅当，σ(φ)=1；φ是L∗可满足的（简称可满足），当且仅当，存在L∗模型φ在其中是真的；φ是L∗有效的（简称有效），当且仅当，对任意L∗模型φ都在其中为真。

命题3.1下列公式是有效的。

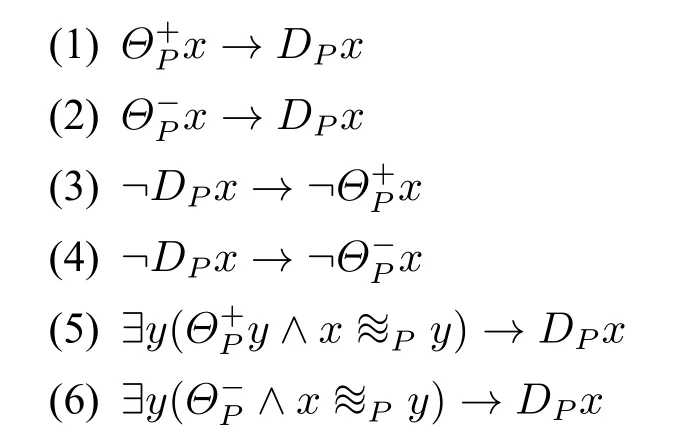
按通常方法易证，证明从略。

设 A∗= 〈D,T,δ,θ,ξ,{≈τ|τ∈ T},η∗〉是任意 L∗结构。可以看出，如果 η∗是η的扩张，那么可以得到，A=〈D,η〉是一个L结构，A∗是A的扩张。在L∗语义中，关于变元、联结词和量词的解释都与L语义相同，所以L∗比L实际上只是多了新增谓词的解释，这表明L∗语义也还是一阶语义。

4 形式结果与直观意义

L∗是在一阶语言的基础上通过增加新的符号和公式得到的用于刻画含糊类的语言。增加的符号有，指标集Π，其中的元素是用于表达含糊类的符号。对任意的P∈Π，L∗增加了谓词符号用于表达以P为主题的相似关系。两个个体在不同的主题下可以有不同的相似关系。如张三和李四在身高方面相似，但是在体型上不相似，所以对于不同的主题有不同的相似关系。分别表示以P为主题的正样本和负样本集。DP表示以P为主题的论域（论题域）。在L∗中可以通过定义得到下面的公式。

定义4.1对任意P∈Π，

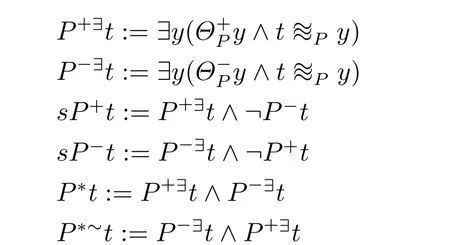
P+∃x表示的是，存在关于P的正样本，x与之相似。P−∃x表示的是，存在关于P的负样本，x与之相似。P+∃x和P−∃x是两个最基本的公式，也是最弱意义的x是P。其他四个公式，都由这两个公式定义得到。

由以上定义得到三种公式P+∃x、sP+x和P∗+x可以说都是某种意义的“x是P”。其中哪一种与我们直观上的“x是P”最吻合？比如，设P为胖子，当我们说“x是胖子”时，所说的更应该是哪一种公式？

P+∃x：有胖子的样本，x与之相似。这是最弱也是最宽泛意义的胖子，是所有胖子都有的底线意义，包括下面的“疑似”胖子。

P∗x：有胖子的样本，x与之相似，也有非胖子的样本，x与之相似。这时x含糊地是胖子，或x是“疑似”胖子。

sP+x：有胖子的样本，x与之相似，且没有非胖子的样本，x与之相似。这是确定的胖子，包括任意的超级胖子，但不包括疑似胖子。

P+∃x是所有胖子都有的底线意义。在此基础上可以有两种情况：或者有负样本x与之相似，得到P∗x，或者没有负样本x与之相似，得到sP+x。

对此我们的直观是，通常情况下P+∃x一般不单独使用，而会在这个基础上，再看负样本如何。如果有负样本与之相似，就是疑似胖子，否则是比较确定的胖子。就这两种情况来说，人们一般不会将疑似胖子称为“胖子”。平时说“x是胖子”时，相对来说还是比较确定的，不包括疑似胖子。如果x是疑似胖子，人们一般会说“x有点胖”，而不说他是胖子。这里还会有一些细节。比如，当人们看某个个体x是不是胖子时，会与心目中的样本比较。当x与更多或更典型的正样本相似，而较少与负样本相似（不是完全没有与之相似的负样本），人们也会说“x是胖子”。详细地研究这个问题，给出更精确的标准，可能需要心理学方面的实验。就当下处理说，如果只是考虑三种情况，两种极端情况和中间情况，可以将“x是胖子”理解为有胖子的正样本与之相似且没有负样本与之相似的个体。

类似地，关于“x是非P”，也有三种公式P−∃x、sP−x和P∗～x3P∗～x的意思是，有非胖子的样本，x与之相似，也有胖子的样本，x与之相似。这时可以说，x含糊地是非胖子。直观上看，对同一个人，如果我们比较含糊地说他是非胖子（即不是很确定他不是胖子），那么说他是胖子也会含糊，而且反之亦然。所以P∗～x和P∗x是等价的。。直观上的“x是非胖子”应该是sP−x。

综上，可以将sP+x和sP−x进一步简化，通过定义引入下面的L∗公式。

定义4.2

Px ∶=P+∃x ∧ ¬P−∃x

P～x ∶=P−∃x∧ ¬P+∃x

该定义中Px即sP+x，也就是直观上的“x是P”。类似地，P～x即sP−x，是直观上“x是非P”。

命题4.1以下公式(1)–(3)是有效的，(4)–(7)不是有效的。

(1)Px→¬P～x

(2)P～x→¬Px

(3)P∗x ↔ P∗～x

(4)¬P～x→Px

(5)¬Px→P～x

(6)Px↔¬P～x

(7)P～x↔¬Px

证明:(1)和(2)按公式定义分别为

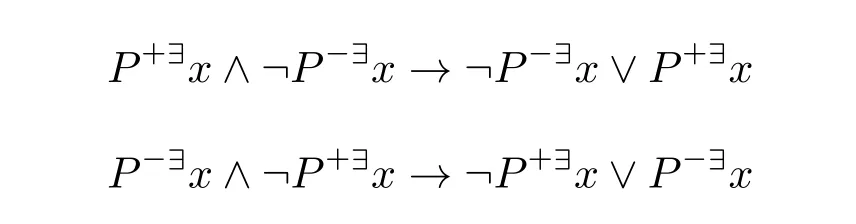
是重言式。(3)由定义可得。(4)和(5)按公式定义分别为

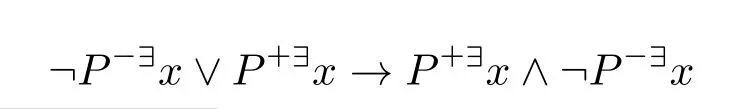
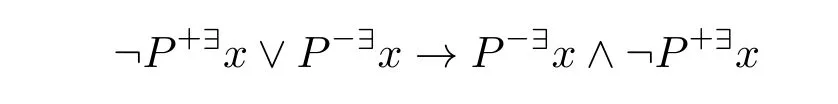
对此容易得到模型使之为假。如果(6)和(7)有效则分别有(4)和(5)有效。 □

在L∗语义中，Px和¬Px是矛盾关系（不可同真，不可同假），但Px与P～x有所不同。从(1)–(2)和(4)–(5)可以看出，Px和P～x不可同真，但是可以同假，这是反对关系，不是矛盾关系。这也表明¬Px与P～x不等值。用于胖子的例子，“x不是胖子”和“x是非胖子”并不等值。通常人们会将“x不是胖子”和“x是非胖子”看成等值关系，二者可以互推，这是因为有论域的作用，默认了是在人这个论域中用这两个表达式。否则，即超出了这个论域，便不能从前者推出后者。(3)表明，“x含糊地是P”和“x含糊地是非P”，此二者是等值的。

命题4.2下列公式是有效的。

(1)Px→P+∃x（例：胖子都有正样本与之相似。）

(2)P～x→P−∃x（例：非胖子都有负样本与之相似。）

(3)P∗x→¬Px（例：如果x含糊地是胖子，那么他还不是胖子。）

(4)P∗x→¬P～x（例：如果x含糊地是胖子，那么他不是非胖子。）

(5)Px→¬P∗x（例：如果x是胖子，那么并非他含糊地是胖子。）

(6)P～x→¬P∗x（例：如果x是非胖子，那么并非他含糊地是胖子。）

证明从略。

这些公式表达了正谓词和负谓词以及中间谓词之间的关系。

命题4.3下列公式是有效的。

(1)Px→DPx

(2)P～x→DPx

(3)¬DPx→P～x

(4)¬DPx→¬Px

(5)Px↔P+∃x∧¬P−∃x∧DPx

(6)P～x↔P−∃x∧¬P+∃x∧DPx

(7)¬Px↔¬P+∃x∨P−∃x∨¬DPx

(8)¬P～x↔¬P−∃x∨P+∃x∨¬DPx

(9)DPx→(Px↔¬P～x)

根据公式的定义和语义定义易证，证明从略。

命题3.1与命题4.3一起，主要表现了样本、正谓词、负谓词和论题域之间的关系，也表现了论题域在刻画含糊类中的作用。

命题3.1(1)–(4)是关于样本和论题域关系的公式。这些公式表明的是，关于某论题的正样本、负样本都在其论题域之中，反之，不在论题域之中的个体不能成为样本，不论是正样本还是负样本。

命题4.3(1)–(4)是关于正谓词和负谓词的与论题域关系的公式。这些公式表明，是P的那些个体和是非P的那些个体都在论题域之中。

根据定义4.2和命题4.3(5)–(8)可以得到下面的有效公式：

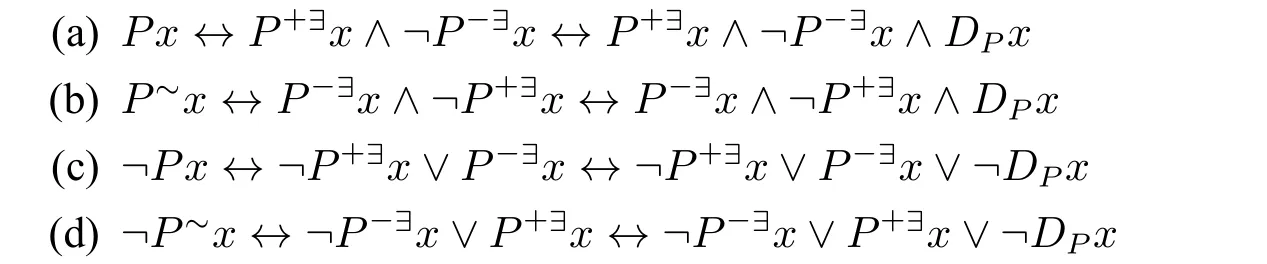
(a)和(b)表明，有无DPx是等值的，这体现了论题域是“隐藏”在背后的这种与正谓词和负谓词的关系和作用。(c)和(d)表明，如果x不在论题域中，那么Px和P～x都为假。命题4.3(9)表达的是，如果限于论题域，Px和P～x是矛盾的。正谓词和负谓词的关系实际上是正谓词、负谓词以及论题词三者之间的关系。这些公式对此给出了合理的表达。

L∗是在L的基础上增加了相似性等词、正负样本谓词和论题词得到的语言，在其中可以通过定义得到表达含糊类的正谓词、负谓词、中间谓词以及相应的公式。从上面对于L∗语义得到的形式结果的解释看，L∗及其语义对此给出了与直观相吻合的刻画。

5 结语

对于含糊性问题有多种研究方法和途经。含糊类是基于样本和相似性得到的类。样本和相似性是基于认知的概念，通过样本和与样本的相似性处理含糊对象是人们在面对含糊性时常用的方法。所以，基于样本和相似性理解提出含糊类及其开展相应的研究是认知主义研究进路。

从样本和相似性的角度看，含糊类有样本收敛和样本发散两大类型，后者应该更为普遍。样本收敛的含糊类也是有核含糊类，可以通过核来处理边界情况。但是因为样本发散含糊类同时也是无核含糊类，所以这个方法不适用于样本发散含糊类。从人们对于含糊对象的实际处理看，除了用正面的样本外，还会用到反面的样本。将这个过程加以抽象，我们提出了负样本以及由正样本和负样本共同处理边界情况的方案。由此得到的含糊类理论更具一般性。在此基础上不仅可以处理样本发散含糊类，也可以处理样本收敛含糊类。

对基于正负样本的含糊类理论的形式刻画是本文要解决的主要问题。对此本文在一阶语言的基础上通过增加正样本谓词、负样本谓词和论题词给出了语言L∗及其语义。在L∗中可以进一步定义正谓词、负谓词以及中间谓词，通过这些表达式可以对于含糊对象及其性质给出相应的刻画。

形式刻画的意义是可以使用形式方法对含糊类问题进行更精确的讨论，进而可以将问题研究引向深入，比如讨论关于含糊性语句的真值问题，高阶含糊性问题等。在认知主义的框架下，基于正负样本的含糊类理论及其形式刻画对于这些问题的解决提供了新的基础，将有可能得到新的理论。

[1]P.Cobreros,D.Ripley,P.Egre and R.van Rooij,2012,“Tolerant,classical,strict”,Journal of Philosophical Logic,41(2):347–385.

[2]K.Fine,1975,“Vagueness,truth and logic”,Synthese,30(3-4):265–300.

[3]P.Lasersohn,1999,“Pragmatic halos”,Language,75(3):522–551.

[4]D.Raffman,1996,“Vaguenessandcontext-relativity”,PhilosophicalStudies,81(2-3):175–192.

[5]N.J.J.Smith,2008,Vagueness and Degrees of Truth,Oxford:Oxford University Press,2008.

[6]R.A.Sorensen,2001,Vagueness and Contradiction,Oxford:Oxford University Press.

[7]M.Tye,1989,“Supervaluationism and the law of excluded middle”,Analysis,49(3):141–143.

[8]T.Williamson,1994,Vagueness,London:Routledge.

[9]L.Zadeh,1965,“Fuzzy sets”,Information and Control,8(3):338–353.

[10]B.Zhou and L.Zhang,2013,“Vague classes and a resolution of the bald paradox”,in J.van Benthem and F.Liu(eds.),Logic Across the University:Foundations and Application,Proceedings of the Tsinghua Logic Conference,Beijing,14–16 October 2013,pp.319–322,London:College Publications.

[11]金岳霖（主编），形式逻辑，1979年，北京：人民出版社。

[12]叶峰，一阶逻辑与一阶理论，1994年，北京：中国社会科学出版社。