联合改进TOPMODEL和PDSI的半干旱区干旱评估模型构建

宫兴龙，付　强，王　斌，关英红，邢贞相，李　衡

（东北农业大学水利与土木工程学院，哈尔滨 150030）

0　引　言

中国由于所处地理位置、气象因素和全球气候的变化导致灾害频繁发生，近年来几乎全国所有省份都发生过干旱，尤其是半干旱区灾害损失严重且有增加的趋势[1-4]。这除与气候变化导致的降雨空间分布异常原因外，也与对干旱发展趋势、预报和预警原理、模型构建和技术工作跟不上等原因有关。主要表现有两点不足：一是对大区域的水-土-植物系统的水流运动过程描述不近完善；二是在干旱评估模型和预报技术上还不成熟，只能依赖于气象预报，还没有建立专业的干旱预报和灾情预警体系。近年来学者探索利用水文模型描述水-土-植物系统的水流运动过程和帕默尔干旱指数联合建立干旱评估模型，张宝庆等[5]利用可变下渗容量模型；李析男等[6]利用土地利用/覆被变化的流域水文模型；许继军等[7]利用分布式水文模型；徐静等[8]采用双源蒸散发能力估算模型等模型；Zhang等[9-10]将帕默尔干旱指数和标准化降水蒸散指数进行了结合，建立基于水文循环物理过程的多时间尺度标准化水分距平指数。帕默尔干旱指数在美国广泛应用于天气-作物预报中[11]。安顺清等[12]对帕默尔干旱指数进行了修正据此提供干旱预报和气候影响评价。为了使帕默尔干旱指标能更好更客观地评价干旱的发生程度，学者进行了大量的研究如杨扬等[13]在修正的帕默尔干旱指数月模式的基础上研制了帕默尔干旱指数日模型。刘招等[14]根据水文气象资料探索泾惠渠灌区的帕默尔干旱模式。李晓辉等[15]引入马利科夫判据与帕默尔指数结合的方法分析干旱特征。刘巍巍等[16]选用了FAO推荐的彭曼-蒙蒂斯公式计算蒸发修正了帕默尔干旱模式。

总之学者探索联合水文模型和帕默尔干旱指数建立干旱评估模型做了大量工作，但目前构建的水文模型和干旱评估模型较少且普遍存在物理基础不强、通用性较差，难于准确地反映半干旱区的降雨和下垫面地形地貌时空变化对水文过程影响，更难于描述干旱的时空变化。为了解决这些问题本文结合半干旱区旱情发展形势的需要从水文循环过程的角度，联合机理性的分布式水文模型LBMGTOPMODEL和PDSI构建干旱评估模型。

1　LBMGTOPMODEL的结构及原理

LBMGTOPMODEL依据水文模型蓝图模型思想改进TOPMODEL而开发的模型。在模型开发过程中，采用先进的模块化设计思路，水循环的每一个环节对应一个子模块，将水文过程分解为二维面降雨量模块、一维蒸散发模块、一维非饱和带水分垂向运移模块、二维坡面汇流模块、一维河流/渠道模块、二维饱和壤中流/地下水模块。在构建过程采用LBM法二维九点速度模型建立坡面汇流过程的程序模块、采用LBM法五速度模型建立河道汇流过程的程序模块、运用LBM法五速度模型求解非饱和区 Richards运动过程、运用达西定律建立饱和区土壤水运动程序模块，进而按照松散耦合方式构建基于LBM栅格（grid）型的分布式TOPMODEL，即LBMGTOPMODEL[17-19]。

1.1　坡面汇流

坡面水汇流可用运动波方程来描述[20-22]：

式中 h为水深，m； u,v分别为沿x和y方向的速度，m/s；g为重力加速度，m/s2；t为时间，s。

采用二维九速度模型推导出式（1）所对应的平衡态分布函数 feq[23-25]：

1.2　河道汇流

河道水流运动采用线性扩散波方程[20]：

式中kc为波速，m/s；kD 为扩散系数，m2/s；Q为河道流量，m3/s。

对上式（3）采用五速模型可得平衡态分布函数：

1.3　非饱和土壤水运移模拟

式中fD 为扩散系数，m2/s；T为导水率，m/s，θ为土壤含水率，m3⋅m-3；z为土壤深度，m。

采用三速模型时，可推得采用式（5）的平衡态分布函数为：

2　干旱评估预报模型建立

按照PDSI评估干旱思路，利用LBMGTOPMODEL模拟获得的水文要素，构建了基于网格单元的LBMGTOPMODEL-PDSI干旱模型。

2.1　水量平衡各分量计算

从水循环角度，Palmer在计算干旱采用简单水量平衡或简化的概念性集总式水文模型，这类方法难于求出水文变量的空间分布情况，更难于求水文常数的空间分布特征。本文利用LBMGTOPMODEL计算出降雨量P、蒸发量ET、根系区缺水量srz、非饱和带缺水量sbar、土壤含水量θ、地面径流和地下径流等水文量，进而计算出气候水文常数，之后计算出干旱指数。

2.2　气候水文常数计算

在计算出每一个网格的水文变量，按照式（7）计算出t日网格gi的补水量R、可能补水量PR、可能径流量PRO、失水量L和可能失水量PL：

式中Pmax,Emax分别为日最大降雨量和蒸发量，mm；θgi为gi网格的田间持水量，mm。

由式（7）计算的变量代入式（8）得网格gi的气象水文常数α（蒸散）、β（补水）、γ（径流）、δ（失水）、K*（气候特征）：

式中ET、PE、R、PR、RO、PRO、L和PL分别为网格gi多年日平均的可能的蒸散发、降雨、补水量、可能补水量、实际径流量、可能径流量、实际失水量和可能失水量，mm。

2.3　气候适宜降水量计算

网格gi的气候适宜降水量采用式（9）获得：

2.4　PDSI干旱指数计算

根据实测降雨与气候适宜降水量之差（d），利用干旱指数x与水分距平值z和持续时间t之间的函数关系，借鉴许继军等[7]干旱评估公式，得:

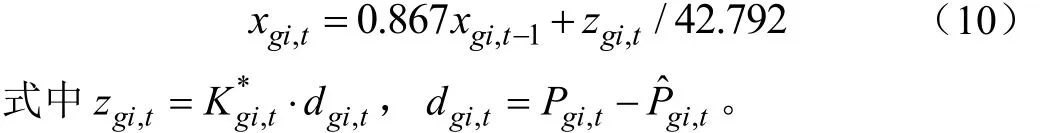
式(10)即为 LBMGTOPMODEL-PDSI干旱评估方法的数学表达式，干旱等级划分[7,26-27]见表1。

表1　PDSI干旱等级划分Table 1　PDSI classification of dry and wet grades

该方法是基于 LBMGTOPMODEL模拟的水文循环数据，因此首先可利用已有的水文气象等数据对历史干湿事件进行描述再现，其次可计算实时干旱事件，推演干旱事件的发展情况。

3　实例应用

3.1　洮儿河流域

本研究选取的典型半干旱区实例为洮儿河察尔森水库站以上的汇水区域为研究流域，其DEM见图1。洮儿河是嫩江右岸最大的一个支流，发源于内蒙古境内大兴安岭东南麓高岳山阿尔山市白狼镇九道沟。年降雨量为350～400 mm，年内降水分布不均匀，主要降雨发生在6—10月。该地区种植的农作物从播种到收获均在5～10月期间。因此本文在计算洮儿河水文常数、评估干旱和预警洪涝时研究时段选在5—10月间。

图1　DEM图Fig.1　DEM scheme

3.2　模型参数选取及验证

选用1964―1989年洮儿河察尔森站流域内的降雨、蒸发和流量等水文气象资料对LBMGTOPMODEL模型进行了率定。将雨量空间分布由五岔沟、索伦、民主、察尔森等11个雨量站采用距离倒数求得。水面蒸发量取库伦和察尔森2个站的均值。流量站选取察尔森站资料。依据参数的物理意义，按照模拟结果最优目标得参数：非饱和带扩散系数0.8 m2/min，下渗参数0.013 m，饱和导水率自然对数1.44，根系区最大蓄水0.067 m，河道扩散系数4.34 m2·min，波速2.36 m/s。采用次洪资料进行验证，结果见表2。参加验证的10场次洪的径流相对误差的绝对值为0.99%～11.48%，平均值为4.45%；洪峰流量相对误差的绝对值为2.51%～12.78%，平均值为5.00%。洪水过程线的确定性系数为0.62～0.93，平均值为0.76，因此LBMGTOPMODEL能较好再现洮儿河流域径流过程。

3.3　水文常数计算及其特征分析

由降雨、蒸发和径流等数据，根据分布式水文模型LBMGTOPMODEL模拟的水文要素，计算出常数值，进而分析常数空间分布和计算时段对常数的影响。

3.3.1常数随计算时段变化特性分析

在研究干旱常数时发现不同文章在计算常数时，所取的时段不同，比如统计时段为月的有文献[5，6，8，10，12-14]，以日的有文献[11]，以年的有文献[15]，以旬的有文献[7]。这就出现一个问题：时段不同计算的常数之间是否相等，有什么样的关系。由于年时段与日、旬和月时间差距太大，并且应用较少本文暂不考虑。以α值为例绘制了α值与日的关系图见图2。由图2得不同月份α均值随时间变化曲线可以得出，α值是随时间在变化的，但发现以日、旬和月为时段计算的常数α之间联系不明显。

表2　宝清水文站次洪误差统计Table 2　Flood simulation error statistics from Baoqing hydrological station

3.3.2常数空间分布分析

为了描述常数的空间分布特征，本文选用多年 7月月均的常数进行说明见图3。图3给出了常数α、β、γ、δ和K*的空间分布图，从图3中可以看出α、β、γ、δ、K*均呈现出一定的空间分布状态，距离河道越远的地方常数越大。为了进一步说明空间分布特征，绘制出α空间分布概率分布见图3b。从图3a和3b可得出洮儿河流域上α呈现概率分布。因此在计算α时应考虑α的空间分布，不能简单的以一个平均值代替。这种情况对其他常数同样适用，见图3c-f。

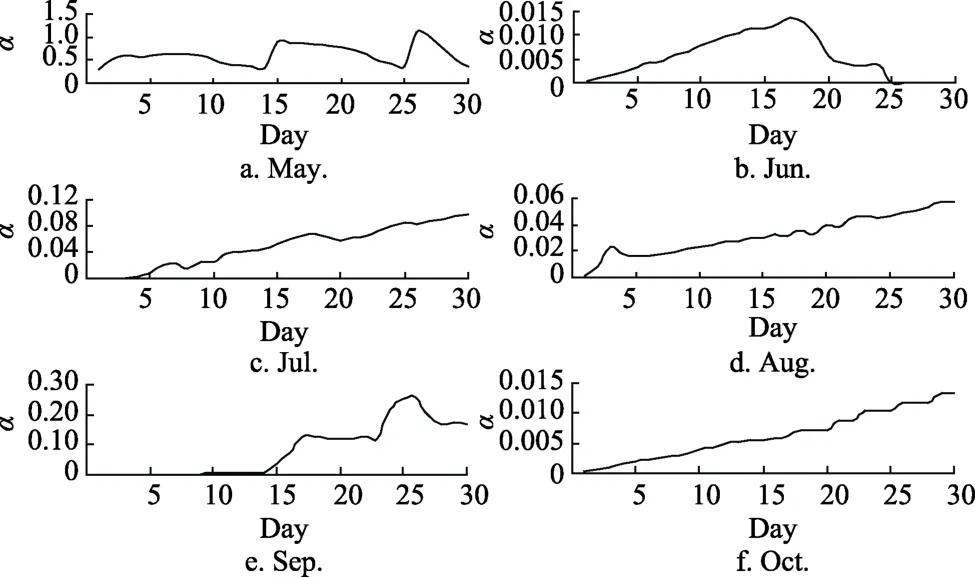
图2　不同月份的α（蒸散常数）随计算时段变化曲线Fig.2　Variation of α with time in different month

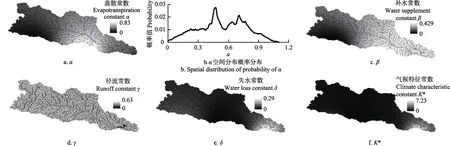
图3　洮儿河五种常数分布图Fig.3　Five constants distributions of Taoer River

图4　6月15日降雨空间分布Fig.4　Spatial distribution of precipitation

3.4　帕默尔旱度指数

为了说明利用 LBMGTOPMODEL描述水流运动过程的合理性、干旱的形成过程和计算的干旱指数合理性，此部分依照降雨后垂向水流运动顺序根系区、非饱和带、地下水和地面径流等展开。

3.4.1降雨空间分布状况

洮儿河流域降雨量比较少，为了便于分析选定比较干旱年份1972年的5月、6月和7月进行分析，此期间降雨发生天数为17 d，降雨量大于10 mm的天数为4 d，分别为6月15日、6月25日、6月27日和7月3日等4 d。6月27日最大降雨为12 mm与6月25日最大降雨量29 mm相比比较小，绘制了6月15日的降雨空间分布见图4。从图4可看出6月15日的降雨中心点偏于下游。由图4可以得出降雨空间分布显著，等值线清楚。

3.4.2根系区缺水量空间分布

利用降雨径流模型模拟可得其根系区缺水量空间分布见图5。从图5可得，距离流域边缘部分缺水量大而靠近河流缺水量小，这与实际流域情况接近。从图5a和图5c可以得出根系区缺水量比较小的区域位于流域下游，缺水量大的区域位于流域上游，这正好与降雨空间分布相对应。图5b的缺水量空间分布是中部缺水量小于流域其他部分，这与降雨空间分布正对应。图5a缺水量范围为12～17 mm，而图5b缺水量范围为4～17 mm，可以发现缺水量在减小。比较图5b和5c图可以发现在经历了7月3日的降雨后研究区域缺水量已经比较小了，大部分缺水量小于10 mm。由图5得根系区缺水量最大值与最小值之差小于图 4缺水量最大值与最小值之差，说明降雨受到蒸发影响和土壤调蓄作用空间差异性减弱，使根系区空间分布趋于均匀。

图5　根系区缺水量空间分布Fig.5　Spatial distribution of water shortage in root zone

3.4.3非饱和带缺水量空间分布

LBMGTOPMODEL模拟降雨渗入土壤的顺序是降雨渗入根系区再流向非饱和带，计算得到非饱和带缺水量如图6所示。从图6可得距离河道越远处缺水量越大，距离河流越近处缺水量越小，这与实际流域情况接近。从图6可以发现非饱和带缺水量变化不大。从图6可以发现非饱和带缺水量空间分布基本接近。这些是由于降雨量对非饱和带的影响不显著，或者说半干旱区根系区缺水量比较大，一般降雨难于满足。这符合半干旱区特点，一般降雨对土壤根系区影响大，对非饱和带影响较小。

图6　非饱和带缺水量空间分布Fig.6　Spatial distribution of water shortage in unsaturated zone

3.4.4径流空间分布

径流包括地面与地下径流，在模拟径流时发现地下径流量变化不大，并且主要集中在河道周围，与地面径流相比量比较小，因此给出了地面径流空间分布见图7。从图 7可以得地面径流主要集中在河道周围，其他部分径流量与河道相比比较小。从径流数据分析可得6月15日最大径流深为77mm，到了6月25增加为128 mm，再7月3日时已增大到225 mm，因此可以说降雨对地面径流量产生了显著影响。

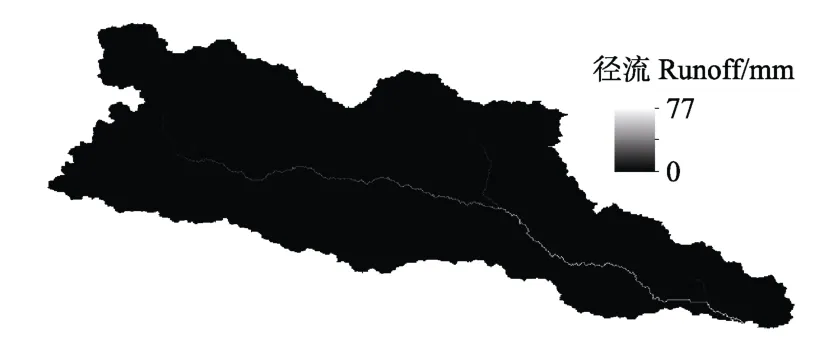
图7　6月15日地面径流空间分布Fig.7　Spatial distribution of surface runoff

3.4.5旬帕默尔旱度指数

联合LBMGTOPMODEL和PDSI干旱评估方法计算的洮儿河1972年的旬干旱指数如图8所示。由5月降雨数据分析可知 5月降雨总量小于蒸发，因此其干旱程度在加深见图8a。6月份洮儿河开始降比较大的降雨，在6月15日（图4）发生降雨，降雨中心在流域下游，局部降雨量达到14 mm。从图4、图5可以发现降雨影响到根系区缺水量使旱情发展速度减缓。由图 6非饱和带缺水量（对于饱和情况的缺水量）空间分布、图 4降雨空间分布和图 5根系区缺水量空间分布得非饱和带缺水量空间分布变化与降雨和根系区缺水量空间分布变化相关性差，这是由于降雨对非饱和带缺水量影响不明显，则可得降雨减缓旱情发展速度有限，这在图8b得洮儿河还是处于干旱状态可以体现。在6月25日时发生了一场较大的降雨，发现根系区缺水量明显减少而地面径流明显加大，但由于前期干旱和 10d的大量蒸发，旱情还是在继续发展，这一规律可以从图 8的图例极值和空间分布近似性得以体现：图 8b图例极值为−17，而图 8c极值为−19.8；两幅图的干旱情况都是下游干旱程度明显大于上游。在7月1日−10日之间降雨量比较大，尤其是7月3日降雨量比较大，从图5-图7可以发现旱情明显缓解，但还是处于干旱。由图8a和8b可得距离河道越远其干旱程度越大，这是由于流域边缘部分汇集地面和地下径流少，而河道附近地面和地下径流的汇水越多。

3.4.6与降水距平指标比较分析

从水循环角度讲，干旱起因是降雨偏少，但是受大气、日照和下垫面综合影响，因此是一个综合水文现象。本文联合LBMGTOPMODEL和PDSI构建的干旱评估模型正是从水循环视角分析干旱，在求得降雨、蒸发、根系区缺水量、非饱和带缺水、地面径流和地下径流等基础上计算干旱指数，进而评价一个地区干旱情况，能够较好地模拟干旱的发生和发展过程，尤其是能够体现出前期的降水丰枯和土壤水分盈亏对后期旱情发展的影响。至于土壤墒情、水分亏缺量、降水距平和降水蒸发差等指标仅仅是依据水循环过程的某一个或两个量而对干旱情况进行评价。如降水距平指标是仅是从降水角度去衡量一个地区的旱涝情况，显然难以反映降水后直至流到流域出口过程中的其他因素的影响。以1972年6月中下旬为例，利用降雨距平法计算得 4旬降雨距平，后两旬见图9。从图9可以看出，利用此法计算的距平百分数具有等雨量线特征，呈现条带状，很好地反映了降雨与多年平均降雨空间的差值。与图9对比发现，图9的空间分布距离河道近处和远处位于同一图例处值相等，这与实际情况不符。由图4到图7描述的水运动过程可以看出降雨经过这些因素的影响后呈现出的干旱情况如图8所示与图9差别很大。因此本文构建干旱评估指标较好地反映了旱情的发展变化状态。

图8　特定时间点旬干旱指数Fig.8　Drought index at specific time points in a periool of ten days

图9　不同时间点降水距平Fig.9　Precipitation anomaly at different time points

4　结　论

对半干旱区春旱不断，而半干旱区分布式水文模型和干旱评估模型较少、计算干旱指数时公式出现一定问题和一般计算干旱的方法不能体现水文常数空间分布等问题，本文联合LBMGTOPMODEL和帕默尔干旱指数评估方法构建半干旱区干旱评估模型，在洮儿河实际应用得到如下结论：

1）利用洮儿河流域 1964–1989年的水文气象资料对 LBMGTOPMODEL进行了检验，检验结果表明LBMGTOPMODEL可以较好的模拟洮儿河流域的水循环过程。

2）发现常数α（蒸散），β（补水），γ（径流），δ（失水）和K*（气候特征）等均呈现出一定空间分布状态，尤其是K*空间分布的差异性最明显。常数随着计算时段不同有变化。

3）联合LBMGTOPMODEL和帕默尔干旱指数构建的干旱评估模型从水循环视角分析干旱，在求得降雨、蒸发、根系区缺水量、非饱和带缺水、地面径流和地下径流等量基础上计算干旱指数，进而评价一个地区干旱情况，能够较好地模拟干旱的发生和发展过程，尤其是能够体现出前期的降水丰枯和土壤水分盈亏对后期旱情发展的影响。

4）从1972年6月中下旬为例，利用降雨距平值与基于LBMGTOPMODEL-PDSI干旱评估模型的干旱指数对比分析得，本文构建的干旱评估方程综合了水文循环过程多变量，考虑干旱影响因素较全面。

5）提出的干旱评估模型LBMGTOPMODEL-PDSI，如结合预报信息和方法可对旱涝灾情的进一步发展趋势进行预报和预警，再加上救灾和救助法，不仅能为评估和预报灾情提供数学方法和智力支持，而且可以为抗旱提供救助计划，这将“被动抗旱”局面扭转为全面的“主动防旱”。

[参考文献]

[1] 吴普特，赵西宁. 气候变化对中国农业用水和粮食生产的影响[J]. 农业工程学报，2010，26(2): 1－6.Wu Pute, Zhao Xining. Impact of climate change on agricultural water use and grain production in China[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(2): 1－6.(in Chinese with English abstract)

[2] 张建云，王国庆，刘九夫. 气候变化权威报告 IPCC报告[J]. 中国水利，2008(2): 37－40.

[3] 顾颖，刘静楠，林锦. 近60年来我国干旱灾害特点和情势分析[J]. 水利水电技术，2010，41(1): 71－74.Gu Ying, Liu Jingnan, Lin Jin. Analysis on characteristics and situation of drought disasters during past 60 years in China[J]. Water Resources and Hydropower Engineering，2010，41(1): 71－74 (in Chinese with English abstract)

[4] 袁文平，周广胜. 干旱指标的理论分析与研究展望[J]. 地球科学进展，2004，19(6): 982－991.YuanWenping, Zhou Guangsheng. Theoratical study and research prospect on drought indices[J]. Advances in Earth Science, 2004, 19(6): 982－991. (in Chinese with English abstract)

[5] 张宝庆，吴普特，赵西宁，等. 基于可变下渗容量模型和Palmer干旱指数的区域干旱化评价研究[J]. 水利学报，2012，43(8): 926－933.Zhang Baoqing, Wu Pute, Zhao Xining, et al. Study on regional drought assessment based on variable infiltration capacity model and palmer drought severity index[J]. Journal of Hydraulic Engineering, 2012, 43(8): 926－933 (in Chinese with English abstract)

[6] 李析男，谢平，李彬彬，等. 变化环境下不同等级干旱事件发生概率的计算方法：以无定河流域为例[J]. 水利学报，2014，45(5): 585－594.Li Xinan, Xie Ping, Li Binbin, et al. Probability calculation method for different grade drought event under changing environment-Taking Wuding River basin as an example[J].Journal of Hydraulic Engineering, 2014, 45(5): 585－594. (in Chinese with English abstract)

[7] 许继军，杨大文. 基于分布式水文模拟的干旱评估预报模型研究[J]. 水利学报，2010，41(6): 739－747.Xu Jijun，Yang Dawen. New model for drought estimation and prediction based on distributed hydrological simulation[J]. Journal of Hydraulic Engineering, 2010, 41(6):739－747. (in Chinese with English abstract)

[8] 徐静，任立良，刘晓帆，等. 基于双源蒸散与混合产流的Palmer旱度模式构建及应用[J]. 水利学报，2012，43(5):545－553.Xu Jing, Ren Liliang, Liu Xiaofan, et al. Establishment of palmer drought severity model based on two-source potential evapotranspiration and hybrid runoff model[J]. Journal of Hydraulic Engineering, 2012, 43(5): 545－553. (in Chinese with English abstract)

[9] Zhang Baoqing, Zhao Xining, Jin Jiming, et al. Development and evaluation of a physically based multiscalar drought index: The Standardized Moisture Anomaly Index[J]. Journal of Geophysical Research:Atmospheres, 2015, 120:11575–11588.

[10] Zhang Baoqing, He Chansheng. A modified water demand estimation method for drought identification over arid and semiarid regions[J]. Agricultural and Forest Meteorology,2016, 230－231: 58－66.

[11] Palmer W C. Met eorological Drought. Research Paper, No45,1965.

[12] 安顺清，邢久星. 修正的帕默尔干旱指数及其应用[J]. 气象，1985，11(12): 17－19.

[13] 杨扬，安顺清，刘巍巍，等. 帕尔默旱度指数方法在全国实时旱情监视中的应用[J]. 水科学进展，2007，18(1): 52－57.Yang Yang, An Shunqing, Liu Weiwei, et al. Application of Palmer drought severity index method to real time drought survey in China[J]. Advances in Water Science, 2007, 18(1):52－57. (in Chinese with English abstract)

[14] 刘招，燕爱玲，乔长录. Palmer旱度模式在渭北旱塬泾惠渠灌区的应用研究[J]. 干旱地区农业研究，2010，28(3):259－264.Liu Zhao, Yan Ailing, Qiao Changlu. Research on application of Palmer drought model in Jinghuiqu irrigation area[J]. Agricultural Research in the Arid Areas, 2010, 28(3):259－264. (in Chinese with English abstract)

[15] 李晓辉，杨勇，任传友. 东北半干旱地区Palmer干旱指数特征分析方法[J]. 吉林农业大学学报，2013，35(3): 317－323.Li Xiao hui, Yang Yong, Ren Chuanyou. Drought Characteristics Analyzing Method Based on Palmer Index in Northeast Semi-arid Region[J]. Journal of Jilin Agricultural University, 2013, 35(3): 317－323. (in Chinese with English abstract)

[16] 刘巍巍，安顺清，刘庚山，等. 帕默尔旱度模式的进一步修正[J]. 应用气象学报，2004，15(2): 207－216.Liu Weiwei, An Shunqing, Liu Gengshan, et al. The farther modification of palmer drought severity model[J]. Journal of Applied Meteorological Science, 2004, 15(2): 207－216. (in Chinese with English abstract)

[17] 宫兴龙，芮孝芳，付强，等. 基于格子玻尔兹曼方法的流域汇流数值模型[J]. 水力发电学报，2014，33(2): 12－17.Gong Xinglong, Rui Xiaofang, Fu Qiang, et al. A numerical model of watershed concentration based on Lattice Boltzmann method[J]. Journal of Hydroelectric Engineering,2014, 33 (2): 12－17. (in Chinese with English abstract)

[18] 宫兴龙，付强，邢贞相，等. 基于格子玻尔兹曼法的TOPMODEL建模与应用[J]. 农业机械学报，2015，46(7):181－186.Gong Xinglong, Fu Qiang, Xing Zhenxiang, et al. Modelling and application of TOPMODEL based on LBM[J].Transactions of the Chinese Society for Agricultural Machinery, 2015,46(7): 181－186. (in Chinese with English abstract)

[19] 宫兴龙，付强，王斌，等. 丘陵-平原-湿地复合区降雨径流数值模型[J]. 农业机械学报，2016，47(11): 227－234.Gong Xinglong, Fu Qiang, Wang Bin, et al. Numerical model of rainfall runoff in hills-plain-wetland compound area[J].Transactions of Chinese Society for Agricultural Machinery,2016, 47(11): 142－149. (in Chinese with English abstract)

[20] 薛禹群，谢春红. 地下水数值模拟[M]. 北京: 科学出版社，2007.

[21] 张德良. 计算流体力学教程[M]. 北京: 高等教育出版社，2009.

[22] 吴颂平，刘赵淼译. 计算流体力学基础及其应用[M]. 北京:高等教育出版社，2013.

[23] 张东辉. 格子玻尔兹曼方法在水文学中的应用研究[D].南京：河海大学，2008.Zhang Donghui. Lattice Boltzmann Method and Some Application to Hydrology[D]. Nanjing:Hohai University,2008. (in Chinese with English abstract)

[24] 王兴勇. Lattice Boltzmann方法及其在流场分析中应用的研究[D]. 南京: 河海大学,1998.Wang Xingyong. Study on the Theory and Application in Hydraulic Computation of the Lattice Boltzmann Method[D].Nanjing: Hohai University, 1998. (in Chinese with English abstract)

[25] 张小娜，冯杰，张东辉，等. 坡面流格子Boltzmann 方法与Preissmann 隐式差分法模拟[J]. 农业机械学报，2014，45(10): 132－140.Zhang Xiaona, Feng Jie, Zhang Donghu, et al. Comparison of lattice Boltzmann method and Preissmann implicit difference method in application to overland flow [J]. Transactions of Chinese Society for Agricultural Machinery, 2014, 45(10):132－140. (in Chinese with English abstract)

[26] 王斌，张展羽，魏永霞，等. 基于投影寻踪的农业基本旱情评估[J]. 农业工程学报，2009，25(4): 157－162.Wang Bin, Zhang Zhanyu, Wei Yongxia, et al. Assessment of agricultural basic drought based on projection pursuit[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(4)：157－162. (in Chinese with English abstract)

[27] 姚玉璧，张存杰，邓振镛，等. 气象、农业干旱指标综述[J]. 干旱地区农业研究，2007，25(1)：185－189，211.Yao Yubi, Zhang Cunjie, Deng Zhenyong, et al. Overview of meteorological and agricultural drought indices[J].Agricultural Research in the Arid Areas, 2007, 25(1): 185－189, 211. (in Chinese with English abstract)