关于类比思想在高中数学中的应用探究

亳州市第一中学 安徽亳州 236800

高中数学相关题目类型较多，且涉及诸多基础理论知识，因此，学生在学习高中数学时应重视基础理论知识的积累，并通过大量练习巩固已学知识。高中数学题目变式较多，为提高解题效率，学生需要熟练使用不同的解题思想，其中类比思想的应用范围较为广泛。

1 类比思想概述

所谓类比思想，是指在多个研究对象中发现其共同点，在这些共同点之间建立较为紧密的联系，进而降低解决问题的难度。

数学作为一门逻辑性较强的学科，其解题的过程就是对题目进行深入分析的过程。应用类比思想能够发现题目中的有效信息，同时将信息关系网络化，以辅助学生进行解题[1-2]。

2 类比思想在高中数学中的应用

在高中数学不同阶段，类比思想都有着一定的应用。学生在解答部分题目时使用类比思想，不仅能够保证解题的正确性，而且还能够提高解题效率。

2.1 简化类比思想

在初中几何部分的学习中，我们认识了勾股定理：在直角三角形中，两直角边的平方和等于斜边的平方，如下图1所示：

图2

图1

根据该定理，我们是否可以对其进行类比推理，也就是在三条边相互垂直的三棱锥中，三个直角三角形的面积S1、S2、S3与底面积S4的关系是否为

对于该推论，我们可以根据三角形的关系进行解答。这一过程可以应用边角关系进行证明，且解题思路清晰。

假设：PA=3，PB=4，PC=2，根据已知条件，三棱锥底面三角形的三条边分别为通过已知的底面三角形各边大小，可以做辅助线（如图2所示），过点B向AC作垂线，与AC交于S点，则根据勾股定理，即AB2-AS2=AB2，求得BS，解得最终答案为

由此可见，在数学解题难度较大的情况下，学生需要考虑一些特殊的解题方法，或者对多种解题思想进行综合运用，从而提高解题效率[3]。

2.2 数形类比分析

对于同属一个类型的题目来说，使用数形变化的解题方法时，学生需要准确把握数形关系，从而保证解题思路的正确性、可靠性。

，且该方程组有唯一解，求该方程组中a的取值。

分析：对于此类题目，学生应当注意对多元函数组进行处理，从中发现已知条件之间的潜在关系，降低解题难度。

解：在对方程组进行分析时我们发现，x2-y+2a=y与y2-x+2a=0关于y=x对称，所以，可以通过类比不同曲线焦点的问题进行解答。如下图3所述：

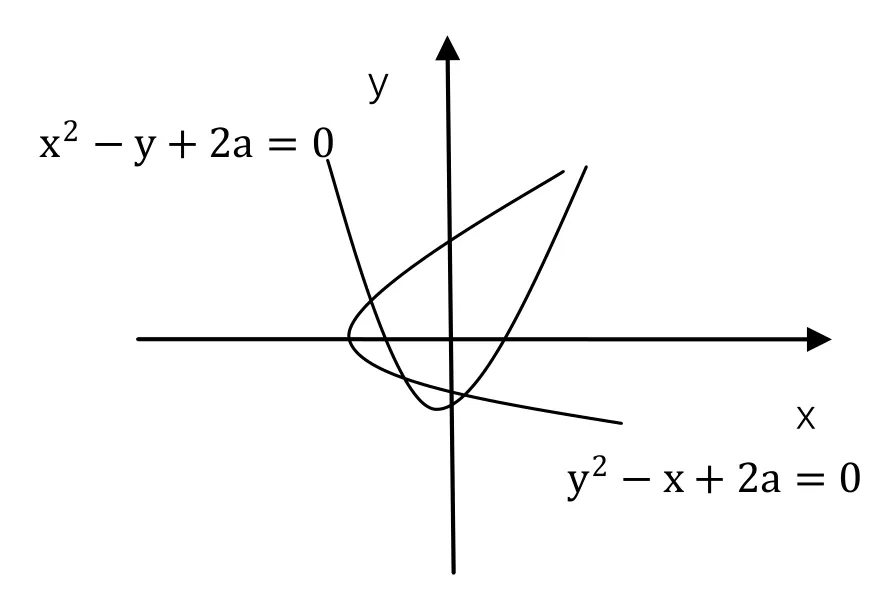
图3

曲线x2-y+2a=0与y2-x+2a=0之间的交点为4个，这不满足题目中解唯一的条件。在数形转换的过程中，其中的数量关系并未发生变化，所以从中能够发现y=x2+2a，同理，另一方程曲线方程为x=y2+2a。

由此可以看出，曲线方程y=x2+2a与x=y2+2a相对于直线y=x对称。因此，若方程组仅有一个解，也就意味着两曲线仅存在一个交点，该交点必然落在直线y=x上。因此，将y=x带入任一曲线方程得：

x2-x+2a=0

其中，△=1-8a=0，则a=1/8。

3 结语

学生在解答高中数学时，应多寻找已知条件的隐藏关系，进而为数学解题提供充分的论据。类比思想的应用，能够提高高中生的逻辑思维能力，使其灵活应用基础理论知识，促进个人解题能力的提升。