圆锥曲线中的等角定理猜想与证明

汤一凡 曹 彬

（贵州省黔西第一中学2020届（18）班 贵州黔西 551500）

过N（t，o）的直线L交双曲线于A，B两点，问是否存在x轴上的一点P，使得直线PA，PB斜率之和为0？

推论1：过点N（t，0）（0＜|t|＜a）的直线L与椭圆

证明：当直线AB与y轴垂直时

只要直线PA，PB斜率存在，直线PA，PB斜率之和都为0.

当直线AB与y轴不垂直时

设直线AB的方程为：x=my+t

联立椭圆方程化简得：（b2m2+a2）y2+2tmb2y+t2b2-a2b2=0

设A（x1，y1），B（x2，y2）

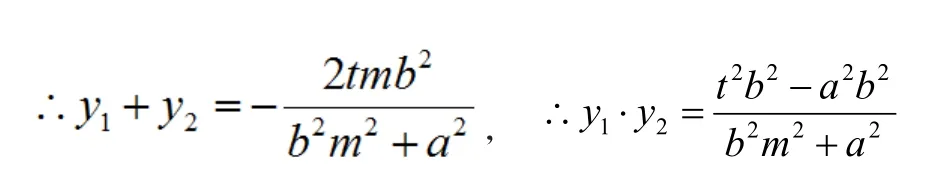
由于斜率存在，所以取分子研究.

由于分母恒为正数，所以又不妨取分子研究.

推论2：过点N（t，0）（|t|＞0）的直线L与双曲线

则X轴上存在一点P（r，0），使得直线PA，PB斜率之和为0的充要条件是

根据推论1的证明过程，充分性是成立的，

下面来证明必要性。

证明：当直线AB与y轴垂直时

只要直线PA，PB斜率存在，直线PA，PB斜率之和都为0.

当直线AB与y轴不垂直时

设直线AB的方程为：x=my+t

联立双曲线方程化简得：（b2m2-a2）y2+2tmb2y+t2b2-a2b2=0

∴y1·（my2+t-r）+y2·（my1+t-r）=0

进一步化简：2my1·y2+t（y1+y2）-r（y1+y2）

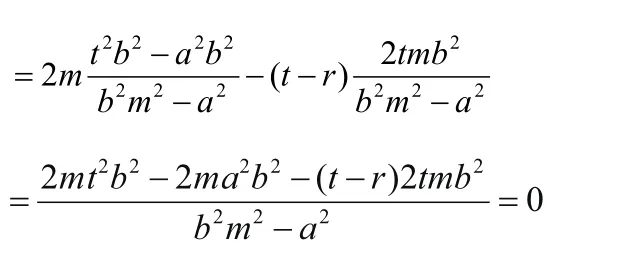
∴2mt2b2-2ma2b2-（t-r）2tmb2=0

∴[t2-a2-（t-r）t]2mb2=0

当直线AB与x轴垂直时，m=0，此时直线PN是线段AB的中垂线，直线PA，PB斜率之和依然为0.

当直线AB与x轴不垂直时，m≠0

∴t2-a2-t2+tr=0，∴

综上所述

过2x轴上的点N（t，0）的直线L与椭圆：或双曲线的一支交于A，B两点