对不动点定理的介绍以及对高中解题构造数列方法的研究

宁波市效实中学 浙江宁波 315000

不动点理论在数学方程中有着广泛的应用，诸如函数方程、微分方程、代数方程等[1]。我们在解答高中数学的数列问题时，就会经常会应用到不动点方程的f(x)=x[2]。不动点理论是研究不动点有无数个性质与求法，因此我们要在构造数列的过程中灵活地应用不动点定理。

1 不动点定理的介绍及选题

1.1 不动点概念

不动点原理又被称为巴拿赫（Banach）不动点原理。简单来讲，就是一个数学函数的定义域中包含该函数的值域，也就是说对于f(x)=x这个方程始终会有一个根存在。因此不动点原理的本质其实就是零点存在性定理。

1.2 选题背景

数学函数中的"不动点"理论虽然是中学教材里的选修内容，但老师也会重点讲解这方面的知识，因为很多同学在这里都会遇到学习上的问题，不能够解答，如果能够熟练掌握，合理地利用”不动点”理论，就会使大家更加容易的解决一些复杂、难以搞定的数学问题。所以近年来“不动点”理论在高中数学中得到了广泛的应用。许多同学也是因为掌握了不动点定理来解决数学问题的方法，从而提高了自己的数学成绩。

1.3 选题意义

根据递推公式来求解数列通项公式、数列的单调性、有界性以及收敛性，这些性质和题型是高考中的热点。其中有一些根据递推公式很难求出通项公式的数列，解决这种数列问题时经常要从函数的性质来出发。在一些高水平的竞赛题中，经常会出现这种综合的数列问题。不仅在竞赛题中，近几年高考题目也有向该题型的方向转化的趋势。因此，该定理的应用还是极为广泛的。

1.4 研究内容

①将不动点原理的迭代思想运用到数列的递推关系中，进而解决通过递推关系难求数列通项公式的问题。

②利用不动点原理的迭代思想，给出对一些数列的有界性性质的证明。

③通过不动点原理，研究数列的单调收敛性质，研究过程中还会运用到特征函数的一些性质，解决高考中的相关题目。

2 不动点定理在数列中的应用

2.1 迭代函数、迭代思想的应用

迭代函数是不断的与自身复合的函数，这个过程叫做迭代[3]。

例：fn+1(x)=f(fn(x))

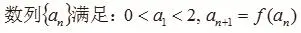
2.2 不动点裂项

对于一阶递推式an+1=f(an)，若f(x)为多项式函数（或分式多项式函数），且α为f(x)的不动点，那么f(an)-α一定有因式 an-α,设 f(an)-α=(an-α)·A

这种改写递推式为裂项形式的方法称为不动点裂项。不动点裂项是改造递推式从而尝试求通项的重要方法，也是得到数列裂项放缩的重要手段。

下面举例几种常见类型的构造形式：

（1）数列单调性、数列放缩综合应用。在数列的综合应用中，我们往往可通过对不动点及迭代函数图像的分析，构造出符合题目结论需要的形式，从而转化为求不等式放缩或求函数最值问题，不动点可谓给构造提供了理论依据，有效避免了盲目变形瞎凑的做法[4]。

几种常见的应用举例：

分析：求范围问题通常可用数学归纳法，本文将另一个角度来阐述数列的有界性问题。

根据前文描述，我们可以通过迭代函数图像，并观察an变化规律，符合（1）中结论。

下面通过不动点的构造，我们来证明：

题目显然与不动点有关，首先，利用绝对值不等式对式子进行变形：

3 结语

通过对不动点的学习，在解答高中数列问题时，可以利用其图像对题目所求内容进行对比，进而利用不动点进行构造，最后通过等比、等差放缩或进行裂项，取倒数、取对数等手法进行求证。只要掌握了不动点，就是掌握了考试的一大利器。