基于虚拟力的危化品仓储堆垛定位校正算法*

戴　波，周泽彧,2，安海洋,2，李雁飞，任海胜,2

(1.北京石油化工学院 信息工程学院，北京 102617；2.北京化工大学 信息科学与技术学院，北京100029)

0　引言

危化品大多以堆垛的形式在仓库中储存，但因为其具有危险性的特点[1]，国家在《常用危险化学品贮存通则》中对危化品仓储中堆垛的“五距”有明确的规定。目前，大多数危化品仓库仍采用人工作业的形式对堆垛进行布置摆放，对于违规操作和安全预警缺乏有效的监控手段。而目前对“五距”的监测手段主要有视频监控、激光扫描和定位技术法[2]。其中，定位法是利用室内定位技术对仓库内堆垛进行定位，利用三维重建技术来还原场景布置状态，并通过实时的数据交互达到监控的目的，该方法具有工作人员操作量小、硬件设施轻便、在复杂仓储环境中工作效率较好等优点，可以应用在危化品仓库监测中，进而提高仓库作业的安全性和可靠性。

仓储堆垛监测技术对定位精度有较高的要求，危化品仓库中要求堆垛货物定位精度最少应达到分米级别。在多种定位技术中，超宽带(UWB)技术作为室内定位精度最高的技术，同样满足抗干扰能力强、能耗低的特点[3]，适用于危化品仓储堆垛的监控。危化品仓库环境中，因堆垛摆放、运输作业等问题，在超宽带信号传播中极易受到遮挡，属于典型的非视距NLOS环境[4]，在这种环境下，可能出现定位的坐标偏离真实位置的情况，进而使得无法还原真实的堆垛环境，影响危化品堆垛“五距”的测量准确性和稳定性。

针对UWB定位精度的问题，一般采用提高算法精度和补偿定位误差2种方法解决。文献[5]利用权值筛选确定初始值，利用泰勒级数展开算法对UWB定位精度校正，提高了精度；文献[6]针对实际测量中误差较大的问题，通过引入可信度因子做内三角质心法来补偿误差，在工业车间中应用效果较好；文献[7]利用参考点补偿的方法，对标签测量坐标进行校正，实验结果显示提高了精度。但是，在实际危化品仓库作业中，除需要考虑参考点设置的位置之外，参考点误差矢量的确定和参考点作用范围也是影响精度的重要部分。由于多径、遮挡、绕射等现象干扰较大[8]，在参考点定位测量的过程中，会累积大量的随机误差，其均值可能并不能反映标签定位的偏移程度。所以，本文采用高斯滤波的方法，选择标签定位高概率处坐标均值作为标签定位偏移量，消除随机误差的干扰，并利用虚拟力算法，通过附近参考点的位置和待测点位置来计算虚拟力合力，得到标签校正定位结果，进而提高危化品仓储堆垛定位的精度。

1　基于UWB的危化品仓储定位误差分析

1.1　UWB信道模型分析

UWB定位技术的原理是通过传感器和标签之间时间间隔极短的脉冲进行通信来确定两者的相对距离[9]，再通过已知的传感器位置信息来得到在室内环境中标签的位置。危化品仓库是一种典型的多径与非视距(NLOS)环境，对于IEEE802.15.4a信道模型来说，信号传播距离与路径损耗的关系[10]如式(1)所示。

(1)

式中：PL0为参考点处路径损耗；n为损耗系数，可随频率变化改变，且与环境中堆垛数量呈正关系；d0通常设置为1 m；S是因阴影效应产生的随机变量，通常认为是均值为1、标准差为σ的正态分布。信号在仓库中传播时的多径时延可以描述为分簇修正模型[11]：

(2)

式中：相位Φk,l服从[0,2π)的均匀分布；αk,l为分簇幅度；Tl,τk,l分别是l簇达到时间和l簇中径k到达时间；L和K分别为簇和径的数量，L服从泊松分布，如式(3)所示。

(3)

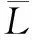
(4)

危化品仓库中UWB理想信道为：

(5)

式中：χ为最先到达的多径分量衰减系数；rrise是功率延迟谱增速;rl为l簇时间衰减系数。由此可见，对于NLOS环境下，UWB脉冲在穿过障碍物时会发生衰减，而不同链路的多径衰减系数是不同的，会对定位精度产生影响。

1.2　基于UWB的定位系统在布置仓库环境中的误差分析

利用UWB定位系统搭建的危化品仓储监控环境由英国Ubisense7000系统作为依托，包括主从传感器、标签以及上位机软件。主从传感器安置在室内顶角处，通过POE交换机连接，形成通讯网络，将主传感器作为时间源，标签固定在堆垛模型中。工作时，标签会发出UWB脉冲信号，传感器接收信号后，Ubisense定位系统利用到达时间差(TDOA)和到达角度(AOA)技术经软件算法计算出标签的位置[12]，该系统的优势在于，只需2个传感器，利用TDOA和1个AOA或者2个AOA，即可确定标签位置，其精度在15 cm左右。利用3D绘图软件还原室内场景如图1所示。系统工作前，需要确定坐标系位置以及在坐标系中各个传感器的位置，Ubisense7000系统会根据这些初始信息处理数据。

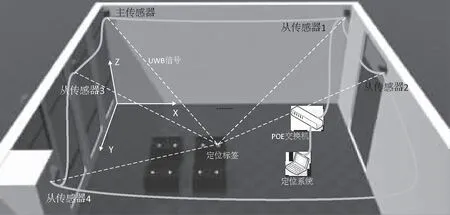
图1　基于UWB定位系统的危化品仓库距离监测示意Fig.1　Sketch map of distance monitoring in hazardous chemicals warehousebased on UWB positioning system

根据UWB信道模型可知，标签距离相近，其信号具有相似的信道环境，其多径衰减系数也是相似的。根据协同定位的思想[13]，在某区域中误差的偏移趋势具有协同性，当设置参考点并测量获得其误差矢量时，其附近的点可以通过该矢量修正，得到真实位置。

在实际危化品仓库中，标签不仅会受到NLOS环境影响和多径效应干扰，同时因为仓库内货物的流动性，理想的信道模型并不具有普适性，定位的精度得不到保证[14]。此外，UWB传感器的系统误差以及标签定位时不同组传感器定位的随机误差也会影响最终的定位结果。文献[15]利用误差矢量指纹的方法，在定位区域中划分参考点网格以及泰森多边形分布，用参考点的测量误差矢量均值来校正待测点的精度，由于多传感器定位时部分传感器与标签之间发生遮挡，即使标签处于静止状态，随着数据量的增加，使得测量的数据也会存在较大的随机误差。此时，利用加权的方法对误差矢量的选取并不能反映该参考点的误差偏移量，所以可采用高斯滤波的方式消除干扰，减少小概率、大干扰数据对整体测量的影响。

2　基于虚拟力算法多参考点矢量校正

2.1　利用高斯滤波建立参考点矢量库

假设二维平面的坐标原点为主传感器的位置，参考点的真实位置为Wi= (xwir,ywir)，设M为t时刻下参考点测量值(xt,yt)集合且每次测量独立，其中t为正整数，通过测量值分析真实值R的概率分布，寻找到最逼近真实值的测量值。假设主从传感器对标签的定位误差分布符合高斯分布，则M的密度函数可以描述为式(6)。

(6)

根据经验，可以选择概率大于经验值60%的范围，σM1和σM2越大，高斯滤波平滑性越好。将此范围的坐标值取出，作几何平均值，即可得到参考点的测量坐标。

选取9个标签，在NLOS下做测试，每个标签测量300组数据，得到结果如图2所示。利用高斯滤波后，得到滤波结果如图3所示，对比均值法测量以及高斯滤波测量数据的结果如表1所示。从图3与表1中可以看出，利用高斯滤波后组成了新的集合，可以认为新的集合已符合无干扰的参考点测量值，消除了由于系统和环境带来的随机误差，但是依旧存在误差偏移，所以本文拟利用虚拟力算法对误差进行补偿。

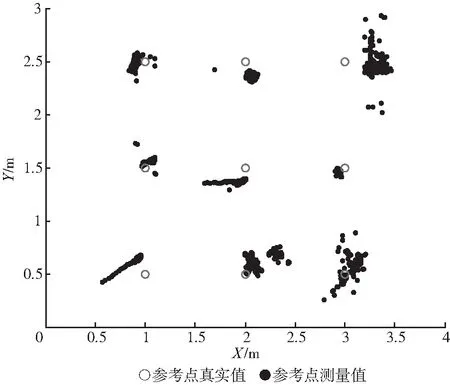
图2　参考点定位测量值数据分布Fig.2　Data distribution of reference point positioning measurement

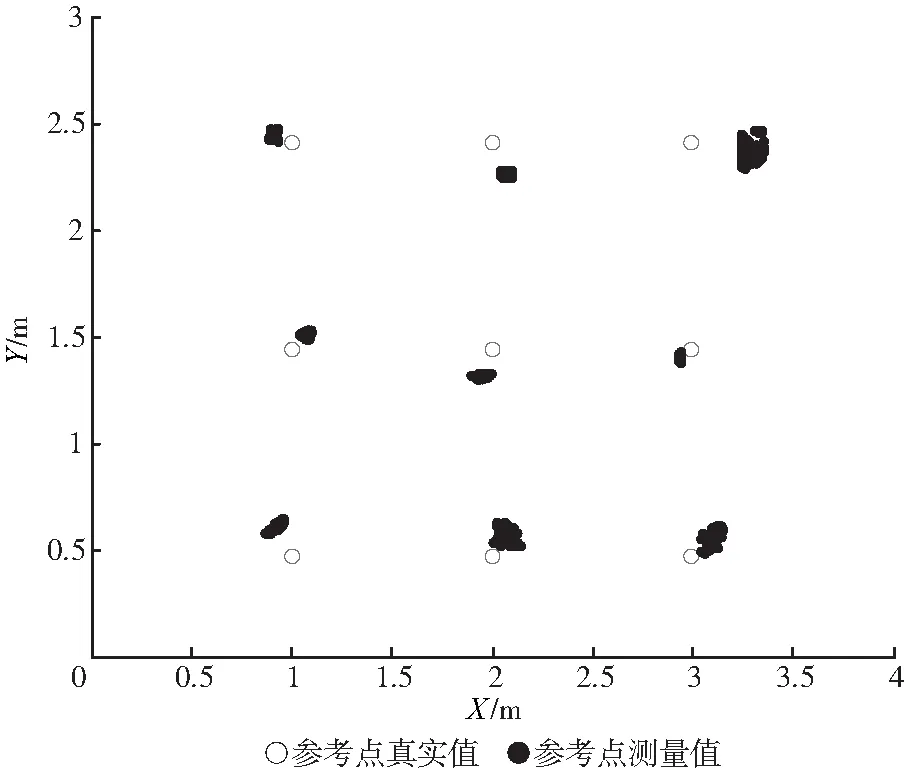
图3　高斯滤波后参考点测量值分布Fig.3　Distribution of reference point measurements after Gauss filtering

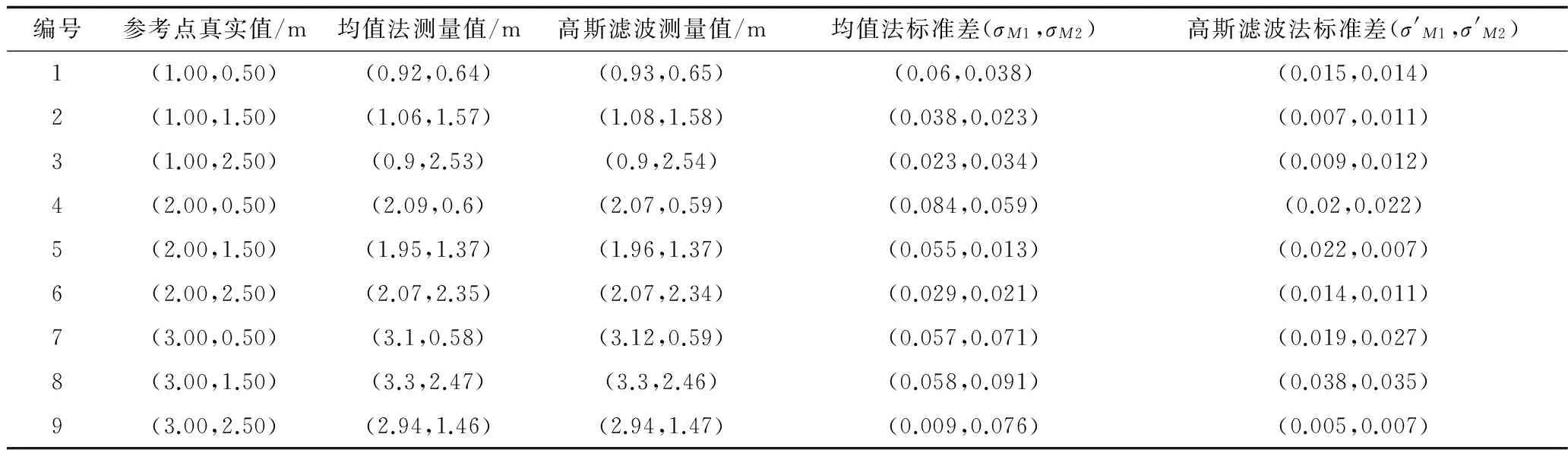
编号参考点真实值/m均值法测量值/m高斯滤波测量值/m均值法标准差(σM1,σM2)高斯滤波法标准差(σ'M1,σ'M2)1(1.00,0.50)(0.92,0.64)(0.93,0.65)(0.06,0.038)(0.015,0.014)2(1.00,1.50)(1.06,1.57)(1.08,1.58)(0.038,0.023)(0.007,0.011)3(1.00,2.50)(0.9,2.53)(0.9,2.54)(0.023,0.034)(0.009,0.012)4(2.00,0.50)(2.09,0.6)(2.07,0.59)(0.084,0.059)(0.02,0.022)5(2.00,1.50)(1.95,1.37)(1.96,1.37)(0.055,0.013)(0.022,0.007)6(2.00,2.50)(2.07,2.35)(2.07,2.34)(0.029,0.021)(0.014,0.011)7(3.00,0.50)(3.1,0.58)(3.12,0.59)(0.057,0.071)(0.019,0.027)8(3.00,1.50)(3.3,2.47)(3.3,2.46)(0.058,0.091)(0.038,0.035)9(3.00,2.50)(2.94,1.46)(2.94,1.47)(0.009,0.076)(0.005,0.007)

2.2　虚拟力校正算法原理

虚拟力的概念最早应用于无线传感器领域[16]，用来提高网络节点的覆盖率。根据UWB信道模型以及定位原理，距离较近的定位标签衰减脉冲相似且所处环境变化几乎相同，这导致其误差和坐标偏移趋势相似。利用协同定位的思想，可以根据标签所在位置的参考点偏移情况，来补偿标签测量，同时，由于标签位置的不同，补偿量的大小是不一致的。所以，本文采用一种虚拟力算法，假设标签在UWB信号覆盖区域的参考点真实坐标和测量坐标处分别存在虚拟的电荷，真实值处电荷设为带有正电，测量值处设为带有负电，所以区域可以根据参考点的选择而形成虚拟的势场，当未知标签放入区域中时，同样假设标签的测量值处存在负电荷，为保持电荷间力的平衡，在待测点周围必定存在一个正电荷，其位置即可视为待测点的校正值。

假设待测点Wi的真实坐标位置为(xwir,ywir)，t时刻时Wi的测量值Wei为(xweti,yweti)(i=1,2,…)。其临近参考点Mj(j=1,2,…)的真实坐标Mrj为(xmrj,ymrj)(j=1,2,…)，通过高斯滤波后得到的测量值Mmj为(xmj,ymj)(j=1,2,…)，则待测点的测量值同参考点的测量值间的距离如式(7)所示。

(7)

待测点的测量值和参考点的真实值间的距离如式(8)所示。

(8)

由此可以得到参考点对待测点的虚拟力，如式(9)所示。

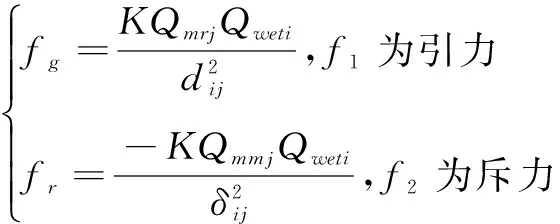
(9)

式中：fg表示Mrj与We间的引力；fr表示Mmj和We的斥力；Qmrj，Qmmj和Qweti分别为参考点真实值、测量值和待测点测量值的带电量，均等于1；K为修正系数，用来修正不同位置电荷对受力的影响。所以，待测点We受到的合力可按式(10)计算得到。

(10)

式中：N为待测点周围参考点数量。为了使We受力平衡，应使校正点Wci的坐标为：

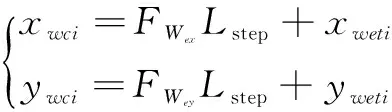
(11)

式中：Lstep是移动步长。(xwci,ywci)即是通过虚拟力校正出来的参考点校正值。

3　实验分析

取UWB传感器覆盖的试验区域4.6 m×3.6 m，为还原堆垛和通道在试验区域的真实情况，通过激光测距得到参考点集的真实值为{(1.30,1.30),(1.90,1.30),(2.90,1.30)，(4.30,1.30),(5.50,1.30),(1.30,1.80),(1.90,1.80),(2.90,1.80),(4.30,1.80),(5.50,1.80),(1.30,3.0),(1.90,3.0),(2.90,3.0),(4.30,3.0),(5.50,3.0),(1.30,3.60),(1.90,3.60),(2.90,3.60),(4.30,3.60),(5.50,3.60),(1.30,4.50),(1.90,4.50),(2.90,4.50),(4.30,4.50),(5.50,4.50)}，临近的4个参考点组成矩形区域，并利用定位数据进行高斯滤波后，得到该矩形区域各参考点的测量值。

在该区域中随机选取200个待测点，计算获得虚拟力算法校正点后，与真实值进行对比，其结果如图4所示，取部分数据列表2。200组数据的真实坐标、测量坐标和校正坐标的结果如图5所示，箭头指向方向为虚拟力法校正矢量。

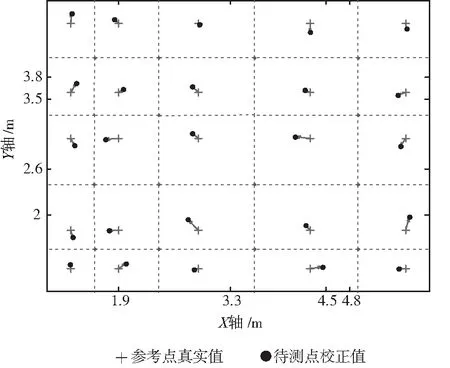
图4　实验参考点真实值及校正值分布Fig.4　Experimental reference point true value and correction value distribution

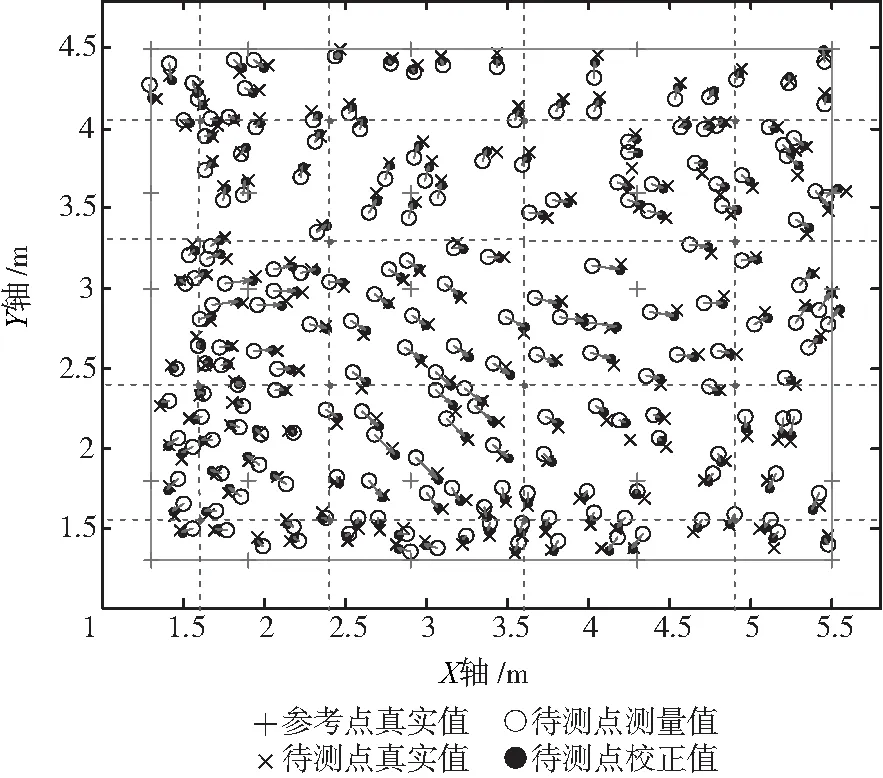
图5　200组实验数据结果显示Fig.5　The results of 200 groups of experimental data

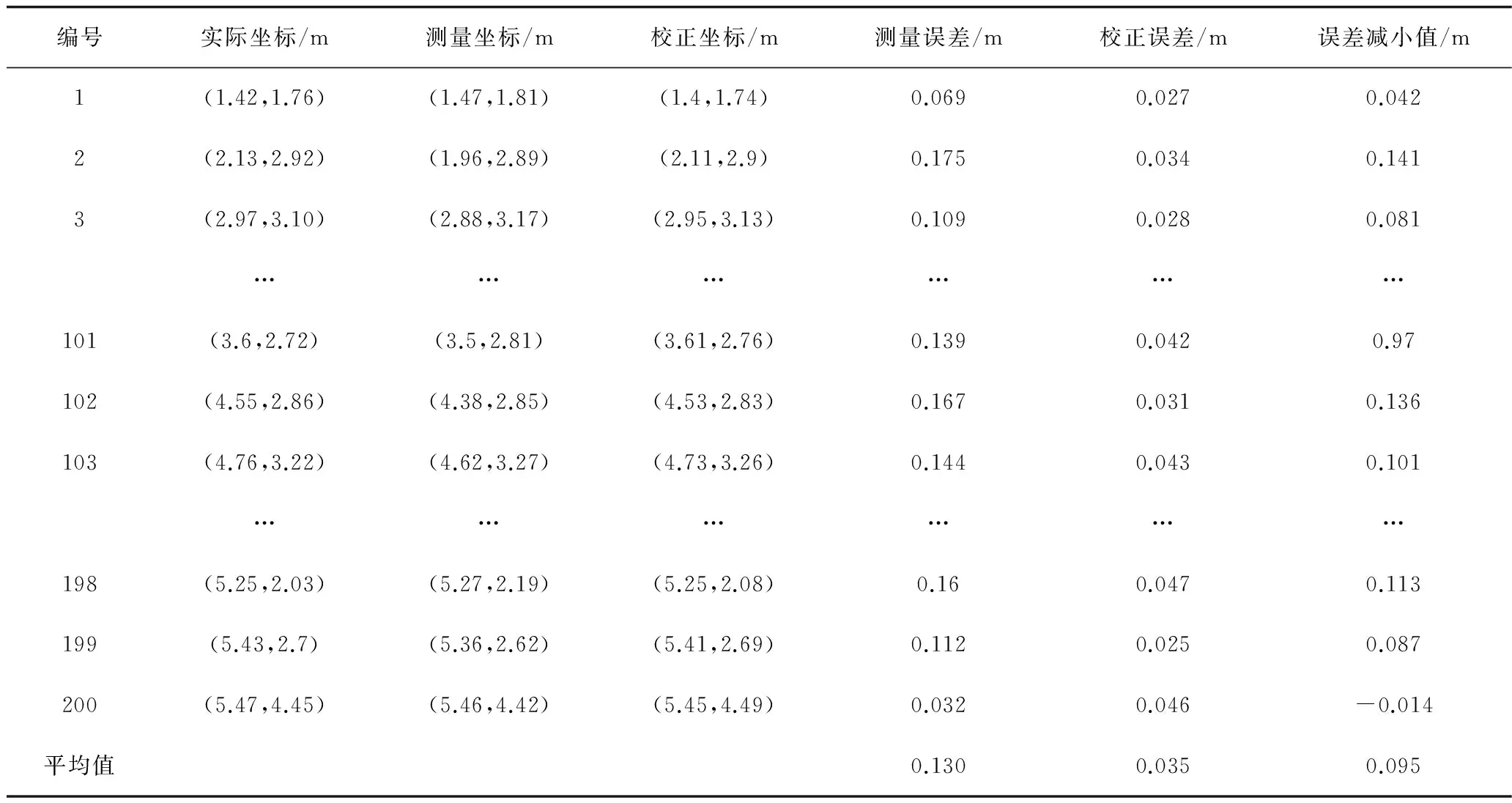
编号实际坐标/m测量坐标/m校正坐标/m测量误差/m校正误差/m误差减小值/m1(1.42,1.76)(1.47,1.81)(1.4,1.74)0.0690.0270.0422(2.13,2.92)(1.96,2.89)(2.11,2.9)0.1750.0340.1413(2.97,3.10)(2.88,3.17)(2.95,3.13)0.1090.0280.081………………101(3.6,2.72)(3.5,2.81)(3.61,2.76)0.1390.0420.97102(4.55,2.86)(4.38,2.85)(4.53,2.83)0.1670.0310.136103(4.76,3.22)(4.62,3.27)(4.73,3.26)0.1440.0430.101………………198(5.25,2.03)(5.27,2.19)(5.25,2.08)0.160.0470.113199(5.43,2.7)(5.36,2.62)(5.41,2.69)0.1120.0250.087200(5.47,4.45)(5.46,4.42)(5.45,4.49)0.0320.046-0.014平均值0.1300.0350.095

从图5中可知，通过校正后，参考点的定位精度均有提高。利用虚拟力算法校正测量点后，误差平均减小了0.095 m，在0.035 m左右，这说明该算法可以提高危化品仓储的非视距环境下的定位精度。

对比文献[7]和文献[15]中的方法，得到定位精度的提升曲线，如图6所示，矢量误差对比结果如表3所示。从图6中可知，本文所提出的方法与其他2种方法在部分数据下的校正精度相似，这是因为2种方法存在校正敏感区，对处于敏感区的参考点来说，其校正效果较好；但对于校正盲区部分，这2种方法同样出现校正效果误差大于测量误差的情况，这主要是由于该位置附近参考点测量时，受到小概率干扰事件的影响，而本文采用高斯滤波后确定的误差矢量和虚拟力算法有效解决了这个问题，具有更好的鲁棒性。

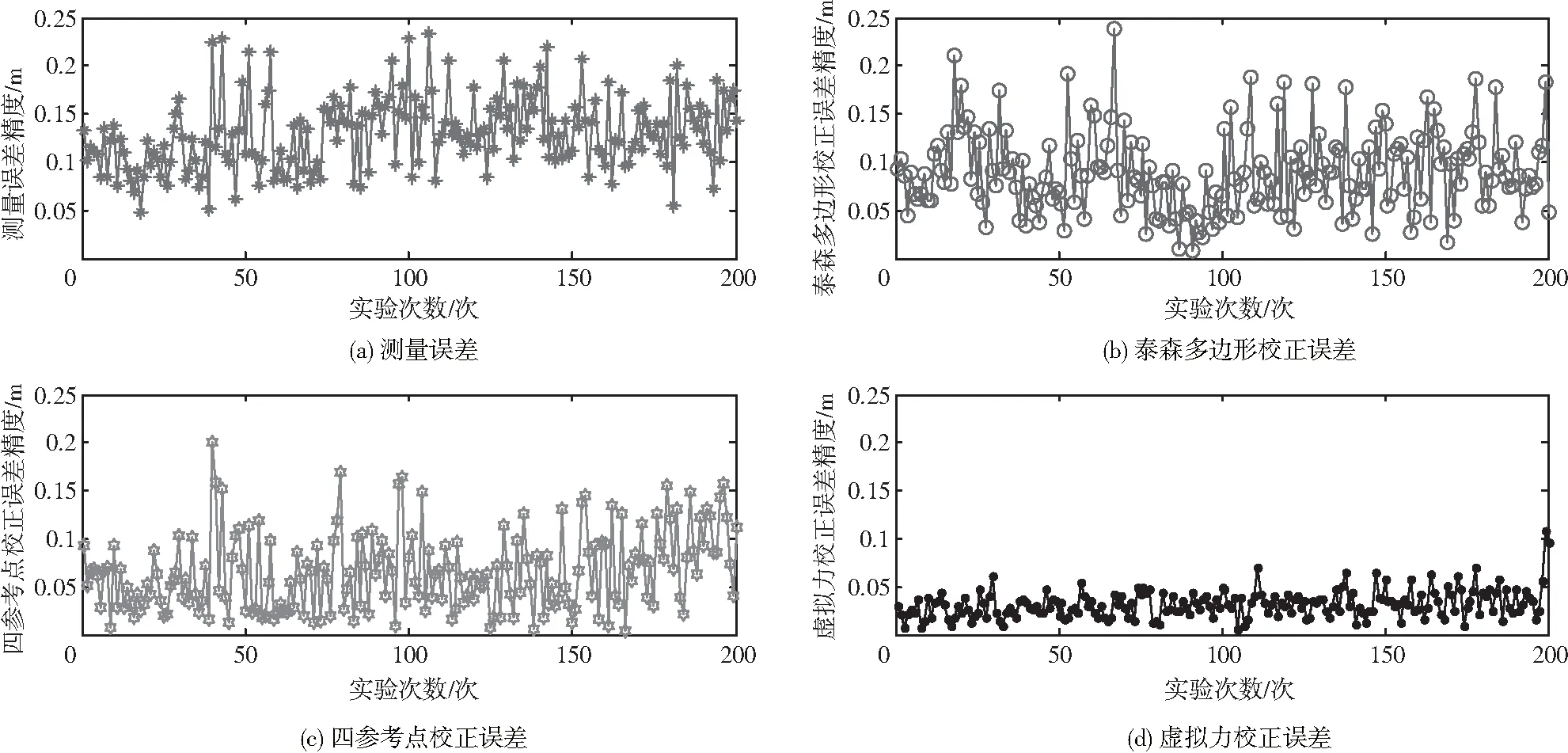
图6　测量误差与3种校正误差对比Fig.6　Comparison of measurement error and three correction errors

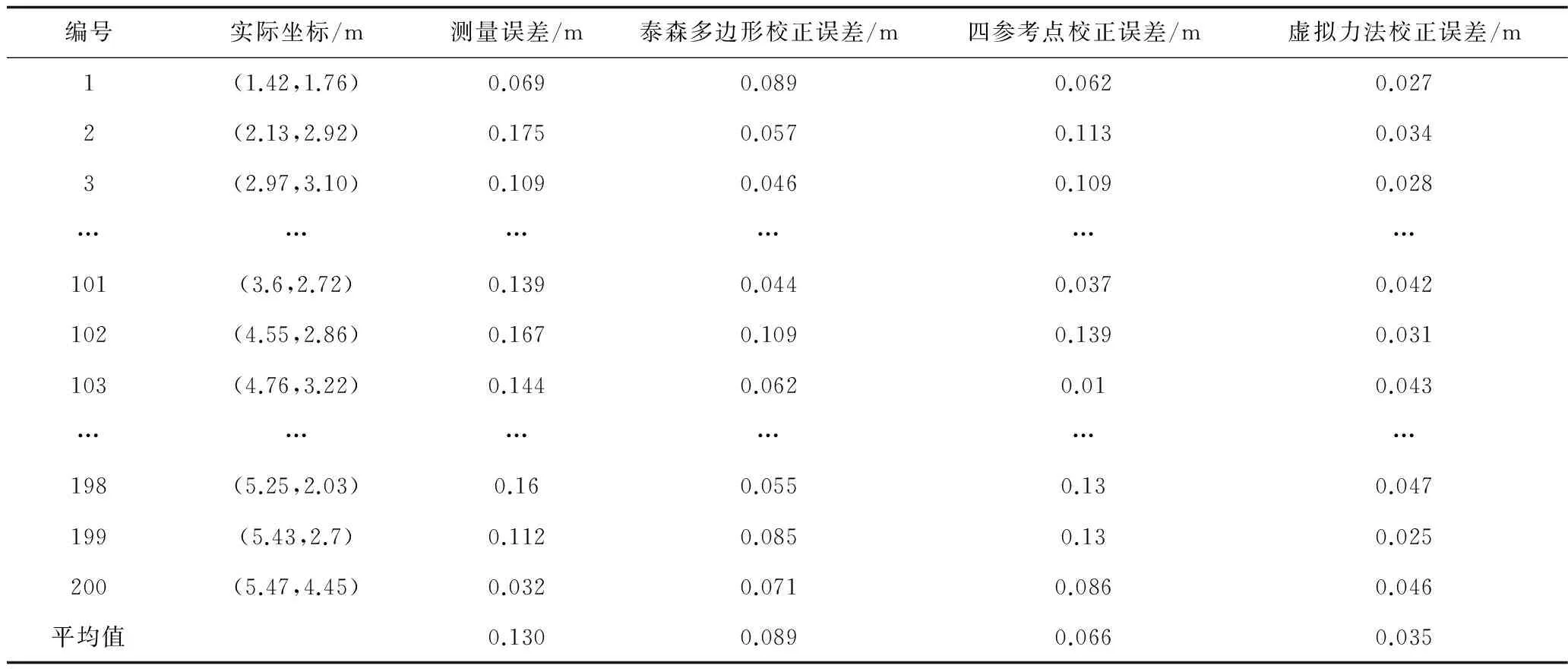
编号实际坐标/m测量误差/m泰森多边形校正误差/m四参考点校正误差/m虚拟力法校正误差/m1(1.42,1.76)0.0690.0890.0620.0272(2.13,2.92)0.1750.0570.1130.0343(2.97,3.10)0.1090.0460.1090.028………………101(3.6,2.72)0.1390.0440.0370.042102(4.55,2.86)0.1670.1090.1390.031103(4.76,3.22)0.1440.0620.010.043………………198(5.25,2.03)0.160.0550.130.047199(5.43,2.7)0.1120.0850.130.025200(5.47,4.45)0.0320.0710.0860.046平均值0.1300.0890.0660.035

4　结论

1)利用UWB定位技术测量危化品仓库堆垛贮存状态是监测危化品堆垛安全距离的重要手段。

2)提出一种基于UWB定位技术的虚拟力算法，用于校正标签精度，对标签的待测点进行补偿校正，通过实验表明，各个待测点在矫正后精度均有提升，提高了UWB定位在危化品仓库中的稳定性，进而能够满足危化品仓储堆垛“五距”监测中的精度要求。

[1]范祥，叶春明，仝伟亮.新形势下我国危化品仓储安全问题研究[J].物流科技，2016(10)：148-151.

FAN Xiang, YE Chunming, TONG Weiliang. Study on the Storage Security of Dangerous Goods in China Under the New Situation[J].Logistics Sci-Tech, 2016(10):148-151.

[2]刘学君，江帆，戴波，等.基于ARM的危化品仓库堆垛安全距离监测装置的研究与开发[J].制造业自动化，2016(4)：11-14，25.

LIU Xuejun, JIANG Fan, DAI Bo, et al.The research and development of stack safe distancemonitoring device for the chemicals warehouse based on ARM[J]. Manufacturing Automation, 2016(4):11-14，25.

[3]WIN M Z, SCHOLTZ R A. Characterization of ultra-wide bandwidth wireless indoor channels: a communication-theoretic view[J]. Selected Areas in Communications IEEE Journal on, 2002, 20(9):1613-1627.

[4]XIAO Zhuo-ling, WEN Hong-kai, MARKHAM A, et al. Non-Line-of-Sight identification and mitigation using received signal strength[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1689-1702.

[5]谢芝玉，刘雄飞，胡志坤.基于Taylor展开的UWB井下定位算法研究与实现[J].计算机工程与应用，2017,53(2)：231-235.

XIE Zhiyu, LIU Xiongfei, HU Zhikun.Research and design of underground coal mine positioning method basedon Taylor algorithm[J]. Computer Engineering and Applications, 2017, 53(2)：231-235.

[6]魏培，姜平，贺晶晶，等.基于内三角形质心算法的超宽带室内定位[J].计算机应用，2017(1)：289-293,298.

WEI Pei, JIANG Ping, HE Jingjing, et al. Ultra wideband indoor localization based on inner triangle centroid algorithm[J]. Journal of Computer Applications, 2017(1):289-293,298.

[7]戴波, 吕昕, 刘学君,等. 基于UWB四参考点矢量补偿的危化品仓储堆垛货物定位方法[J]. 化工学报, 2016, 67(3):871-877.

DAI Bo, LYU Xin, LIU Xuejun, et al. A UWB-based four reference vectors compensation method applied on hazardous chemicals warehouse stacking positioning[J].CIESCJournal,2016,67(3):871-877.

[8]韩涛，宋建勋，王红成.非视距环境下超宽带信号多重绕射仿真研究[J].系统仿真学报，2015(6)：1183-1189.

HAN Tao, SONG Jianxun,WANG Hongcheng.Multi diffraction simulation of ultra wideband signals in NLOS environment[J]. Journal of System Simulation, 2015(6):1183-1189.

[9]STEPHAN A, GUéGUEN E, CRUSSIèRE M, et al. Optimization of linear preceded OFDM for high-data-rate UWB systems[J]. EURASIP Journal on Wireless Communications and Networking, 2008, 10 (2):723-728.

[10]于进刚，卢爱华.UWB信道模型简介[J].西安邮电学院学报，2006，11(1)：29-32.

YU Jingang, LU Aihua.Brief introduction of UWB channel model [J]. JOURNAL OF XI'AN UNIVERSITY OF POST AND TELECOMMUNICATIONS, 2006,11(1):29-32.

[11]汤咏. 超宽带室内无线信道建模[D]. 南京：南京邮电大学, 2014.

[12]TAPONECCO L, D’AMICO A A, MENGALI U. Joint TOA and AOA estimation for UWB localization applications[J]. IEEE Transactions on Wireless Communications, 2011, 10(7): 2207-2217.

[13]PENNA F, CACERES M A, WYMEERSCH H. Cramér-Rao Bound for Hybrid GNSS-Terrestrial Cooperative Positioning[J]. IEEE Communications Letters, 2010, 14(11):1005-1007.

[14]樊甫华，阮怀林.低信噪比下非凸化压缩感知超宽带信道估计方法[J].电子学报，2014(2)：353-359.

FAN Fuhua, RUAN Huailin.Non-Convex Compressive Sensing Ultra-Wide Band ChannelEstimation Method in Low SNR Conditions[J].ACTA ELECTRONICA SINICA,2014(2):353-359.

[15]戴波, 李志超, 刘学君,等. 基于泰森多边形的UWB危化品堆垛仓储货物定位技术[J]. 化工学报, 2016, 67(3):878-884.

DAI Bo, LI Zhichao, LIU Xuejun, et al.UWB location technology of hazardous chemicals stacking storage based onThiessenpolygon[J].CIESC Journal,2016,67(3):878-884.

[16]YI Z, CHAKRABARTY K. Sensor deployment and target localization in distributed sensor networks[J]. Acm Transactions on Embedded Computing Systems, 2004, 3(1):61-91.