不平衡及谐波电网下基于多模块复数滤波器的电网阻抗检测方法

杨 莹，张 兴，李 明

（合肥工业大学电气与自动化工程学院，合肥230009）

高电网阻抗是弱电网的主要电气特性之一[1-3]，电网阻抗特性的变化会对并网逆变器控制环路增益、带宽及控制性能产生影响，甚至引起逆变器并网电能质量和稳定性问题。针对弱电网下并网逆变器的控制，采用基于阻抗的稳定性判据是研究并网逆变器和电网之间交互作用的一项重要方法[4-5]，而该判据需要获取准确的电网阻抗信息，因此，电网阻抗检测具有重要意义。

目前，电网阻抗检测方法主要可以分为被动检测和主动检测，被动检测无需向电网中注入扰动，但其检测结果会受到并网系统中其他并网设备的影响[6-7]；主动检测则需要向电网注入扰动，其最常用的方式为通过向系统中注入非特征次谐波，并提取相应的谐波响应信号计算电网阻抗[8-10]。针对谐波响应信号的提取方法，文献[11]通过采用离散傅里叶变换DFT（discrete Fourier transform）来提取相应谐波，但是，该方案在实际应用中存在谐波频谱干扰和频谱泄漏问题，电网阻抗检测精度会受到影响；针对上述DFT存在的问题，文献[12]采用复数滤波器 CCF（complex coefficient filters）提取相应的响应信号，在理想电网或不平衡电网情况下，能够较准确地实现电网阻抗检测，但在电网电压特定次背景谐波中含量较大情况下，电网阻抗检测精度下降。

针对上述存在的问题，本文提出一种基于多模块复数滤波器MCCF（multiple complex coefficient filters）和非特征次谐波注入的电网阻抗检测方法。所提电网阻抗检测方法使用MCCF实现对公共耦合点PCC（point of common coupling）电压非特征次谐波分量和电流非特征次谐波分量的准确提取，从而经过计算得出电网阻抗的阻性分量和感性分量。本文研究了在电网不平衡及电网背景谐波情况下MCCF提取非特征次谐波的基本原理及设计方法，并从提取精度和动态性能等方面对MCCF的参数进行了优化设计，最后仿真验证了所提电网阻抗检测方法的有效性，并对比分析了在电网不平衡及电网背景谐波下的基于CCF和MCCF的电网阻抗检测情况。

1 电网阻抗检测原理

1.1 三相并网逆变器拓扑结构

图1为典型的三相并网逆变器拓扑及控制结构。图中，Vdc为直流输入电压，Lf和Cf构成LC型滤波器，Rd为阻尼电阻，uga、ugb、ugc为 PCC（point of common coupling）电网电压，iga、igb、igc为 PCC 并网电流，Zg为电网阻抗。

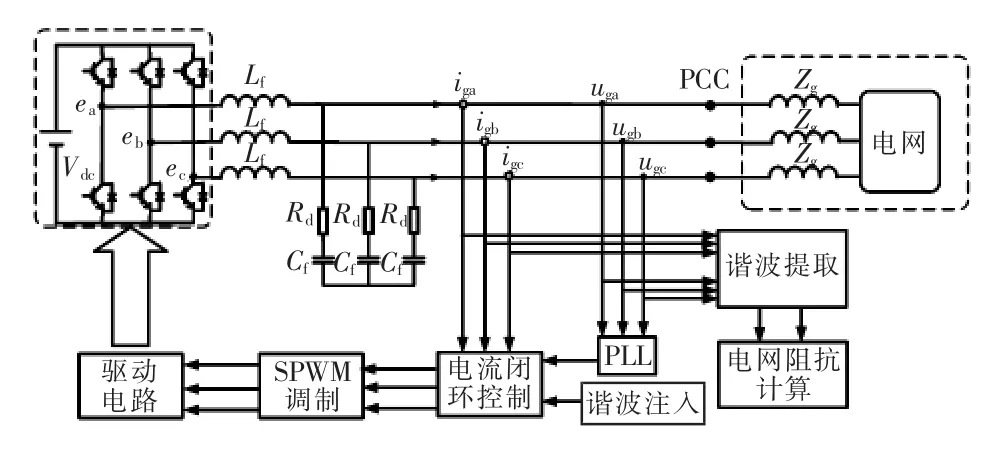
图1 三相并网逆变器拓扑及控制结构Fig.1 Topology and control structure of three-phase grid-connect inverter

1.2 电网阻抗检测原理

如图1所示，在并网系统中，向逆变器控制系统中注入频率为fh的非特征次谐波，然后提取PCC电网电压和PCC并网电流中的非特征次谐波频率fh处的电压谐波响应信号upcc（h）、电流谐波响应信号ipcc（h），其中h表示所注入非特征次谐波分量的次数。根据弱电网下的电感-电阻（L-R）串联模型[13]，得到电网阻抗的阻性分量Rg和感性分量Lg，其L-R模型为

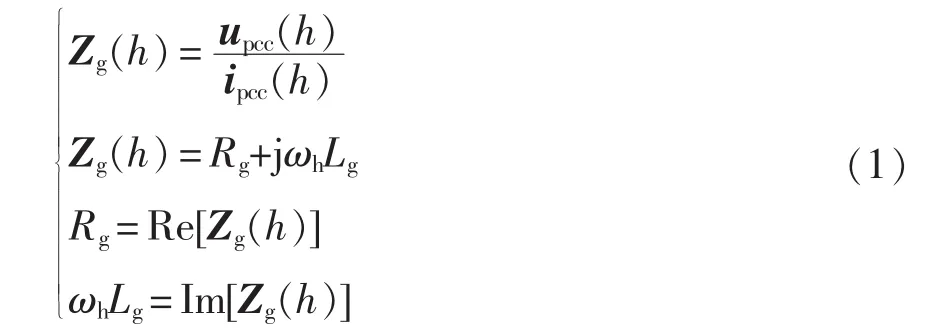
其中：ωh=2πfh。

通过上述分析可知，准确快速检测PCC电网电压和PCC并网电流非特征次谐波分量是电网阻抗检测算法的基础，最常用的DFT谐波检测技术，该方法理论上可以准确提取相应的谐波分量，然而，实际系统中由于采样精度和采样速度的限制以及谐波频谱间的相互干扰，极大影响了其检测计算精度。另一方面，CCF在理想电网或者不平衡电网情况下可以准确提取谐波，但在电网特定次背景谐波含量较高的情况下，谐波测量精度下降。基于此，本文提出采用MCCF提取PCC电压和电流非特征次谐波分量。

2 基于MCCF的电网阻抗检测

2.1 MCCF基本原理

本文所提出的 MCCF 可实现 upcc（h）、ipcc（h）在αβ坐标系下的准确提取。以提取非特征次谐波电压为例进行分析，MCCF的控制框图如图2所示。图2中，ugαβ为PCC电网电压ugabc变换到两相静止αβ坐标系下的分量，为非特征次谐波电压，和为电网电压基波正、负序在αβ坐标系的分量，为电网电压背景谐波在αβ坐标系的分量（n为正整数），ωo为电网电压基波角频率，nωo为电网电压背景谐波角频率，ωc为电网电压基波和电网电压背景谐波截止频率；ωh为MCCF非特征次谐波角频率，ωhc为MCCF非特征次谐波截止频率。

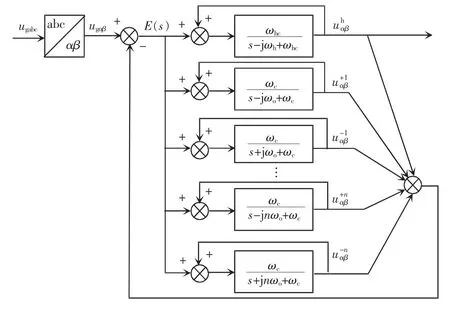
图2 MCCF控制框图Fig.2 Control block diagram of MCCF

图2的MCCF中每个子模块为1阶复数带通滤波器 CBF（complex band-pass filter）。CBF 的传递函数表达式为

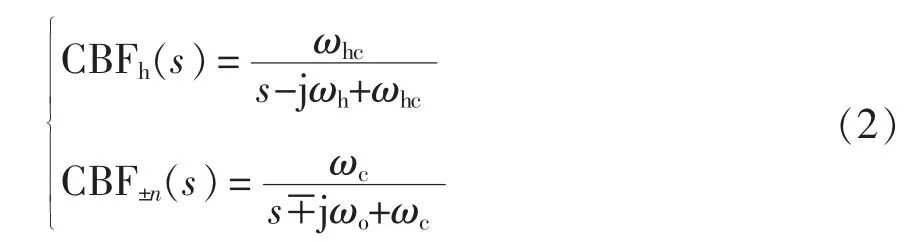
式中：CBFh为 ωh对应的传递函数；CBF±n为 nωo对应的传递函数。

将非特征次谐波分量对应的CBF单位正反馈定义为Ph，电网电压基波正负序和电网电压背景谐波对应的CBF单位正反馈定义为P±n，其传递函数为

式中：Hh（s）为MCCF将非特征次谐波与电网电压中的正负序分量以及电网电压特定次背景谐波分量解耦提取的传递函数。

当考虑电网谐波分量时，一般电网中5、7次谐波含量最大[7]，因此，本文以消除电网5次，7次背景谐波的影响为例，对MCCF提取非特征次谐波的原理进行详细分析，该分析同时适用于消除电网其他次背景谐波的影响。本文研究的不平衡及谐波电网电压主要包括非特征次谐波分量、基频正序分量、基频负序分量、5倍频负序分量和7倍频正序分量。此时的 MCCF 应含有 CBFh、CBF+1、CBF-1、CBF-5和 CBF+75 个模块，则 Hh（s）的表达式为

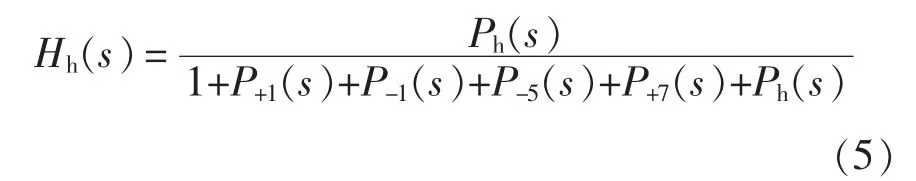
为将MCCF与CCF进行对比分析，相应地得出 CCF 对应的 Hh_pcc（s）表达式为

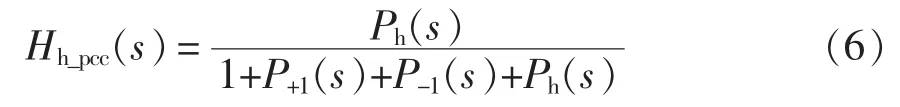
图3为CCF和MCCF的幅频特性曲线。对比发现，两者在所要提取的ωh处幅频特性增益均为1，这表明两种滤波器均可使非特征次谐波分量无衰减地通过。结合式（5）、式（6）与图3， CCF 与MCCF在电网电压基波正负序ωo和-ωo处增益均为0，因此通过CCF与MCCF均可将非特征次谐波分量与电网电压基波正负序分量完全解耦，但与CCF 相比，MCCF 多 了 2 个 零点-j5ωo和 j7ωo,即MCCF在电网特定次背景谐波角频率-5ωo和7ωo处增益也为0，因此MCCF可实现非特征次谐波分量与电网电压基波正负序分量、电网电压5次和7次背景谐波分量完全解耦，从而可以消除电网电压基波正负序分量、电网电压5次和7次背景谐波对所要提取非特征次谐波的影响[14]。

上述以提取非特征次谐波电压为例对MCCF的原理进行了分析，非特征次谐波电流的提取过程与此相同。通过MCCF提取并网逆变器PCC电网电压和PCC并网电流中的非特征次谐波信号upcc（h）、ipcc（h）在 αβ 坐标系下的谐波分量 uhα、uhβ和 ihα、ihβ可实现电网阻抗计算，他们之间的关系为

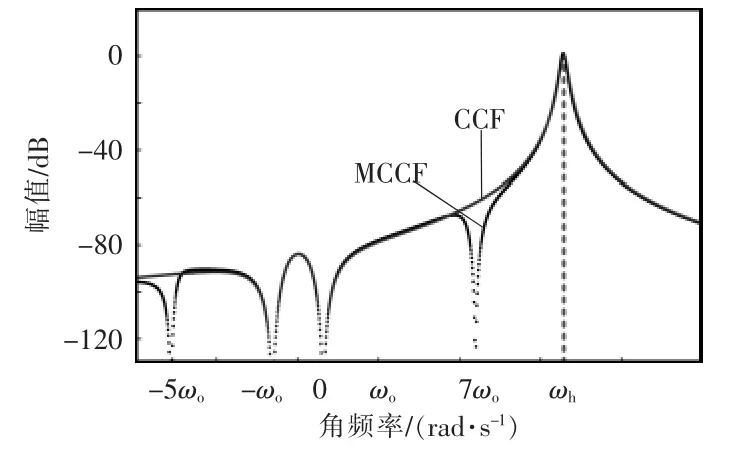
图3 CCF和MCCF幅频特性曲线Fig.3 Magnitude-frequency cures of CCF and MCCF

此时可得电网阻抗的阻性分量Rg和感性分量Lg的表达式为

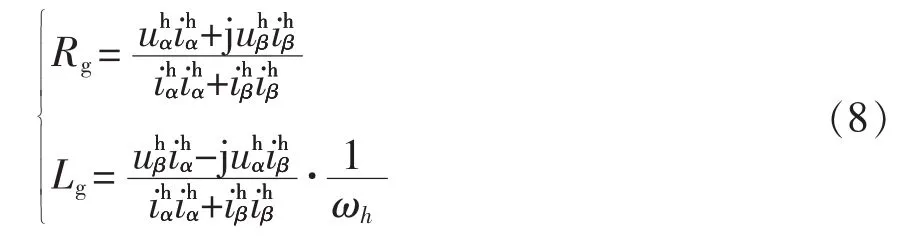
2.2 复数滤波器参数的优化设计及数字实现

为避免电网基波以及电网低频谐波的影响，提高MCCF的动态性能，选取电网基波频率10倍以上的非特征次谐波作为注入谐波。另外，随着注入谐波频率的增大，对DSP的AD采样速度的要求也会显著增加，本文综合这些因素，选择注入的非特征次谐波频率 fh为 525 Hz，ωh为 3 297 rad/s。ωc取为 0.707 ωo，对于 50 Hz 的电网系统，此处 ωc取为221 rad/s[15]。ωhc会影响MCCF的提取精度和动态性能，需要对ωhc进行优化选取。

图4为 ωhc由 100 rad/s到 1 000 rad/s变化时Hh（s）的幅频特性。由图可得，ωhc越小，对电网电压基波正负序分量以及5次、7次背景谐波的抑制能力越强，即相应的电网阻抗检测精度越高，但动态性能会降低，需根据检测精度和动态性能权衡考虑[16]。

图5为MCCF随ωhc变化时的根轨迹。由于MCCF的传递函数的输入和输出均为复矢量，因此图5中的极点分布关于实轴并不对称。闭环极点越远离虚轴，则MCCF调节时间越短；反之，闭环极点靠近虚轴，则调节时间越长[17]。结合提取精度和动态性能综合分析，本文选取ωhc=300 rad/s。

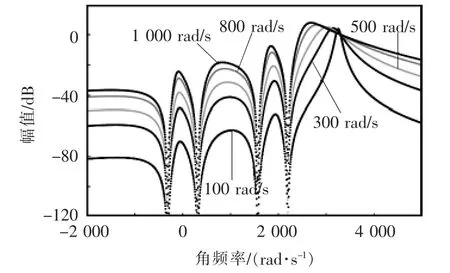
图4 MCCF幅频特性曲线Fig.4 Magnitude-frequency curves of MCCF

图6为MCCF的实现结构，可以看出滤波器由加、减、乘法和积分构成，实际应用中应易实现。

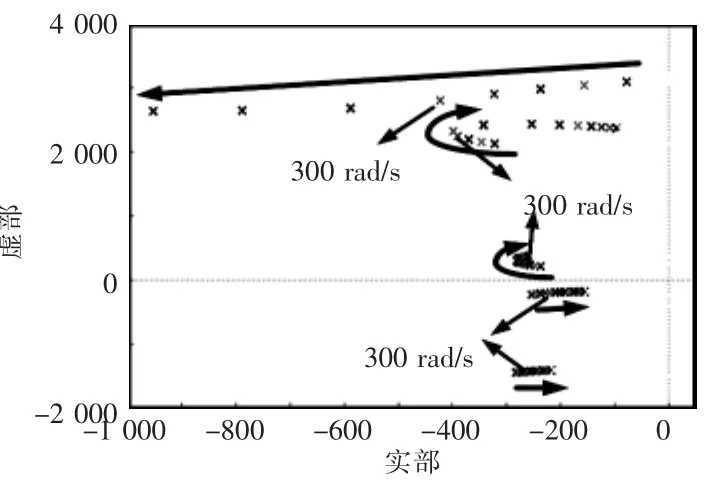
图5 MCCF根轨迹Fig.5 Root locus of MCCF

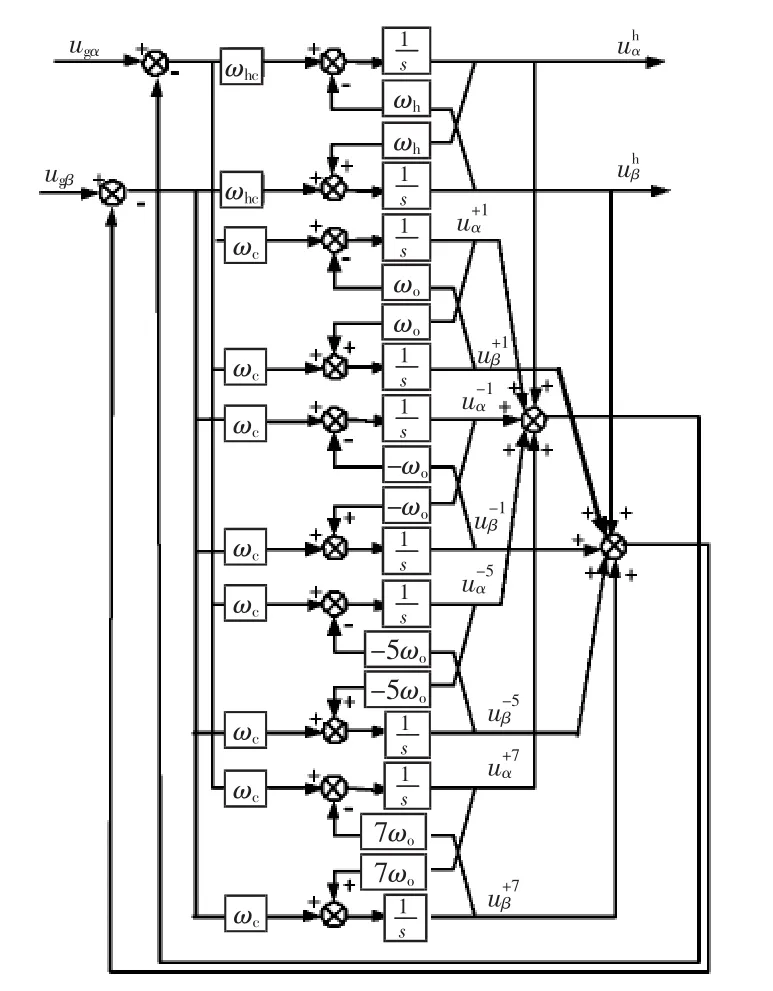
图6 MCCF实现结构框图Fig.6 Block diagram of implementation structure of MCCF

3 仿真验证

根据上述原理分析，按照图1所示系统结构搭建三相并网逆变器仿真模型，对基于MCCF的非特征次谐波注入电网阻抗检测方法进行验证。仿真参数见表1。

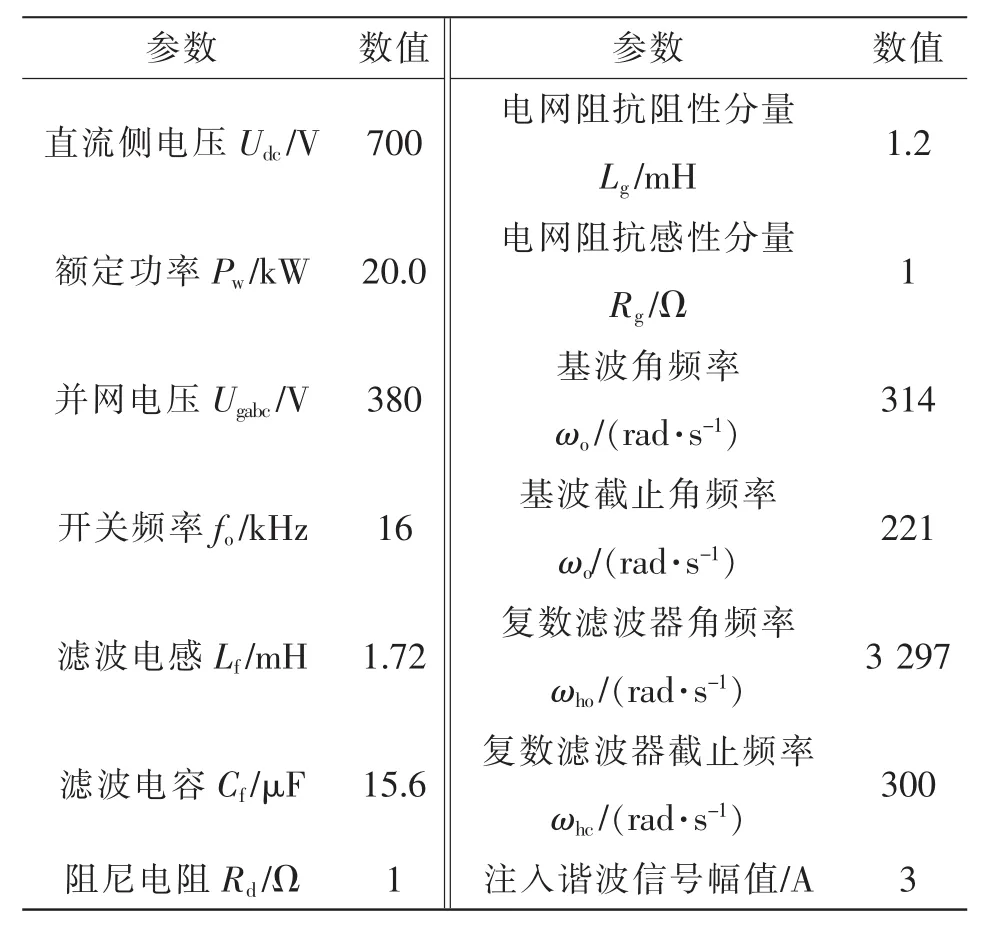
表1 仿真参数Tab.1 Simulation parameters

并网稳态情况下，采用MCCF测量得到的非特征次谐波电压和电流在αβ坐标系下的分量以及根据式（8）计算电网阻抗中的阻性分量和感性分量如图7所示。

仿真模型中，模拟电网阻抗阻性分量1 Ω不变、电感在0.4 s和0.6 s时模拟电网阻抗感性分量变化，采用MCCF提取PCC电压和电流中的非特征次谐波分量，进而检测电网阻抗，其仿真结果如图8所示。其中该方法在电网阻抗发生变化后的动态调节时间为20 ms。

为对比分析不平衡电网下CCF和MCCF检测电网阻抗情况，构造包含负序分量10%的电网电压条件，采用CCF和MCCF检测电网阻抗阻性分量和感性分量，仿真结果如图9所示。由图可见，在0.65 s时电网电压出现三相不平衡情况，基于CCF和MCCF的电网阻抗检测方法经过15 ms的调节时间，可再次准确跟踪检测。

为对比分析不平衡和谐波电网下CCF和MCCF检测电网阻抗情况，构造了包含负序分量10%、5次谐波分量5%和7次谐波分量5%的电网电压条件，采用CCF和MCCF所检测的电网阻抗阻性分量和感性分量，仿真结果如图10所示。由图可见在0.65 s时电网变为不平衡和谐波电网，基于CCF的电网阻抗检测方法无法准确检测电网阻抗，基于MCCF的电网阻抗检测方法经过15 ms的调节时间，可再次准确跟踪检测。

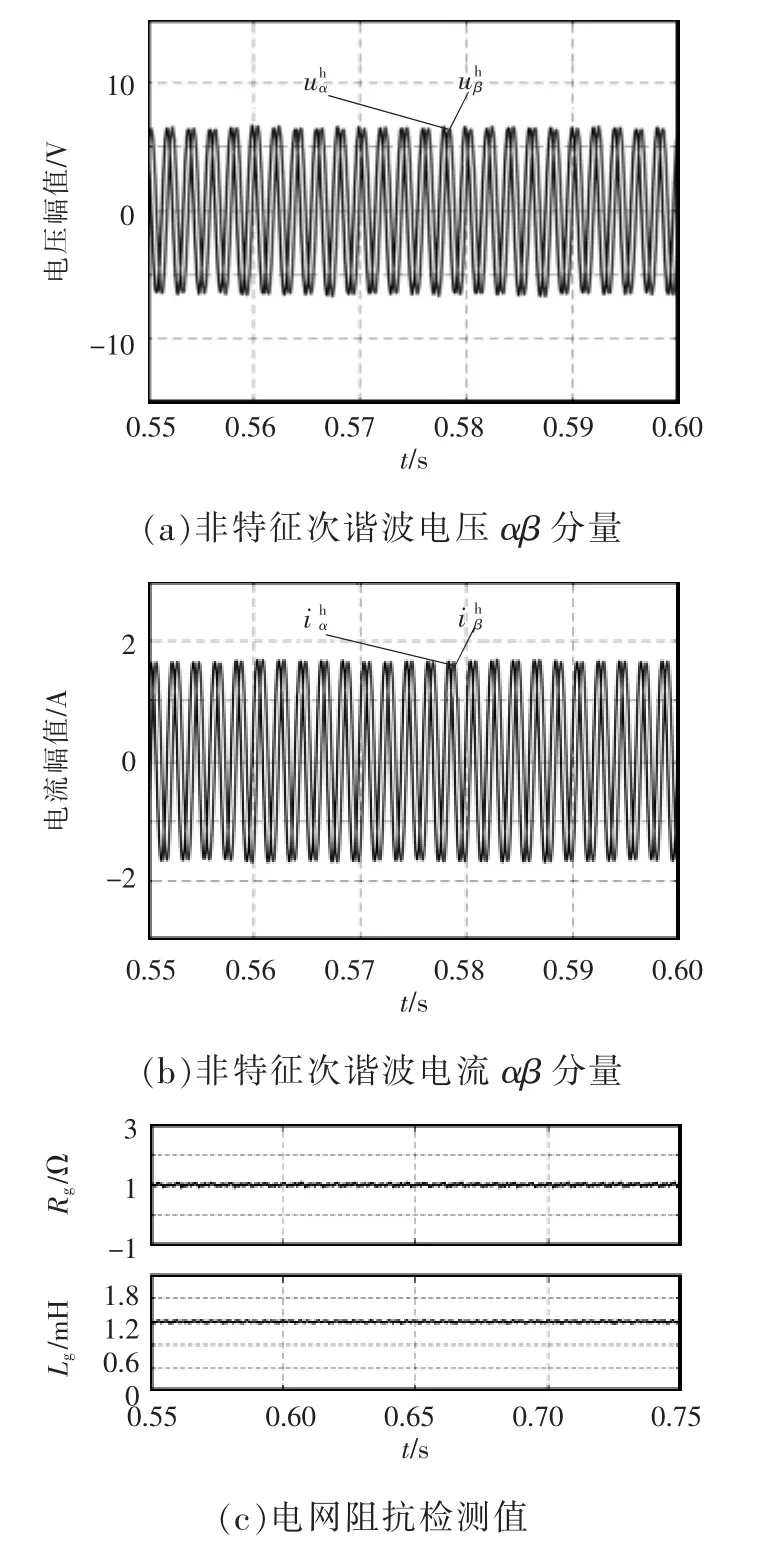
图7 基于MCCF的电网阻抗检测稳态仿真结果Fig.7 Simulation results of grid impedance detection in a steady state based on MCCF

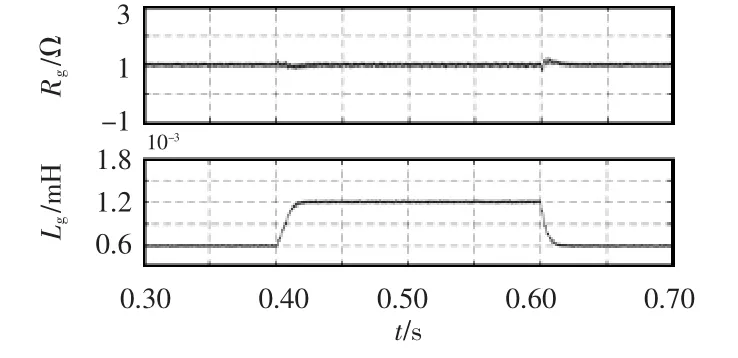
图8 基于MCCF的电网阻抗检测动态仿真结果Fig.8 Simulation result of grid impedance detection in a changing state based on MCCF

以上仿真结果表明，本文所提出的基于非特征次谐波注入MCCF提取的电网阻抗检测方法在电网不平衡和含有谐波分量的情况下均可准确检测电网阻抗，并且具有较好的动态性能。

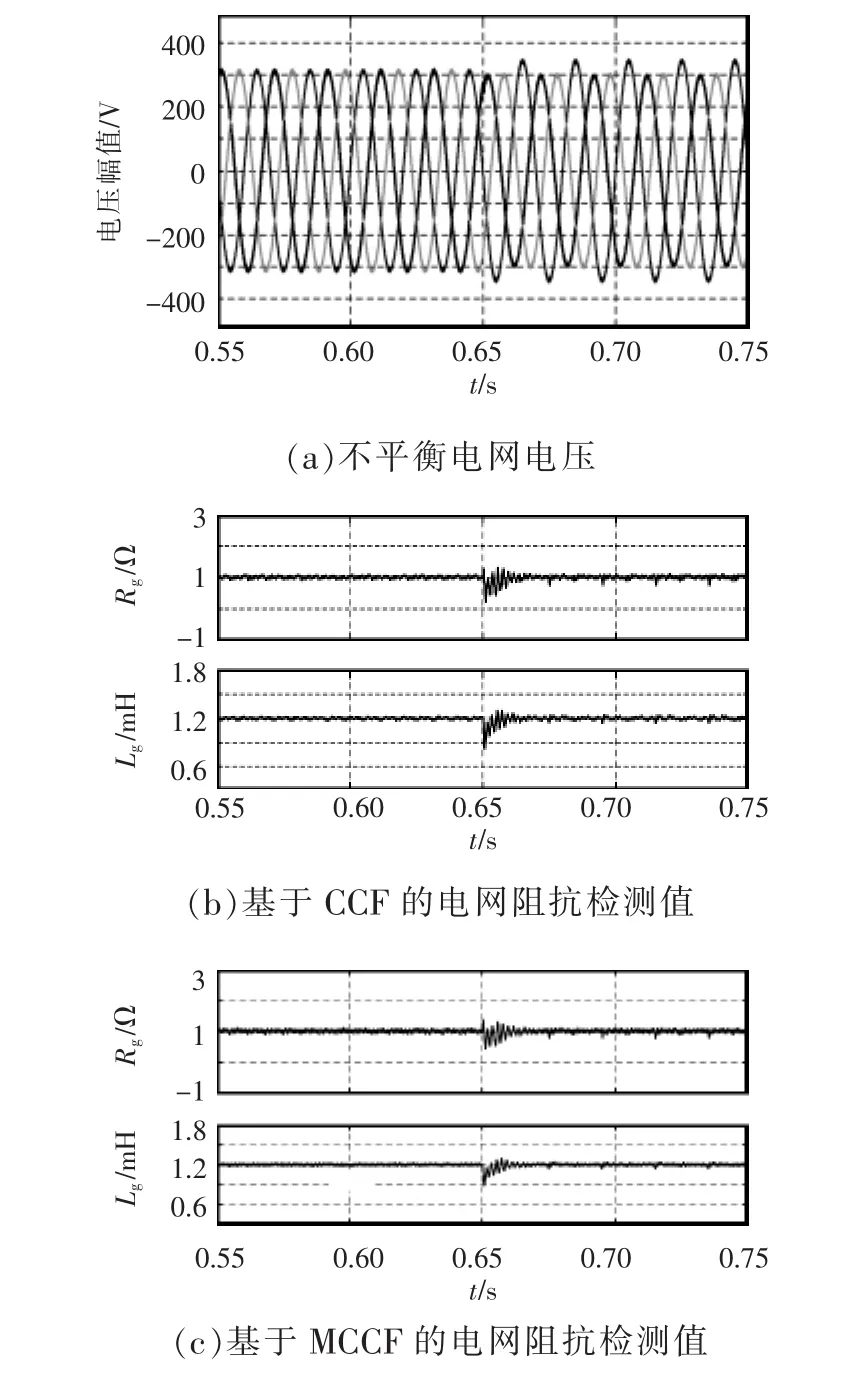
图9 在不平衡电网情况下电网阻抗检测仿真结果Fig.9 Simulation results of grid impedance detection under unbalanced grid voltage

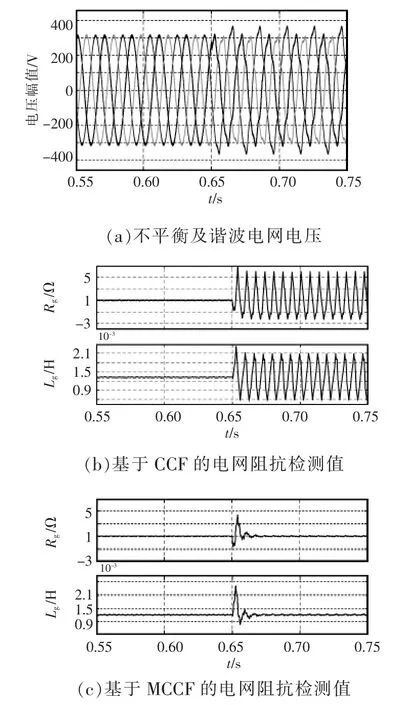
图10 不平衡及谐波电网下电网阻抗检测仿真结果Fig.10 Simulation results of grid impedance detection under unbalanced and harmonic grid voltages

4 结语

本文针对不平衡和谐波电网，提出一种基于MCCF和非特征次谐波注入的电网阻抗检测方法。所提电网阻抗检测方法使用MCCF实现对PCC电压非特征次谐波分量和电流非特征次谐波分量的准确提取，从而经过计算得出电网阻抗的阻性分量和感性分量。仿真研究表明，与基于CCF的电网阻抗检测方法相比，基于MCCF的电网阻抗检测方法在不平衡及谐波电网下可以实现准确检测电网阻抗，并且具有较快的响应速度。与DFT等传统电网阻抗检测方法相比，本文基于MCCF的电网阻抗检测方法具有更好的精确度以及动态性能，实现简单。后续将对以上结论进行实验验证。

参考文献：

[1]Midtsund T,Suul J A,Undeland T.Evaluation of current controller performance and stability for voltage source converters connected to a weak grid[C].The 2nd International Symposium on Power Electronics for Distributed Generation Systems.Hefei,China,2010:382-388.

[2]杨东升,阮新波,吴恒.提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J].中国电机工程学报,2014,34（15）:2327-2335.Yang Dongsheng,Ruan Xinbo,Wu Heng.A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J].Proceedings of the CSEE,2014,34 （15）:2327-2335 （in Chinese）.

[3]李明,张兴,杨莹,等.弱电网下基于加权系数的电网电压前馈控制策略[J].电源学报,2017,15（6）:10-18.Li Ming,Zhang Xing,Yang Ying,et al.Grid voltage feedforward control strategy based on weighting coefficient in weak grid[J].Journal of Power Supply,2017,15（6）:10-18（in Chinese）.

[4]Sun Jian,Bing Zhonghui,Karimi K J.Input impedance modeling of multipulse rectifiers by harmonic linearization[J].IEEE Transactions on Power Electronics,2009,24（12）:2812-2820.

[5]Sun Jian.Impedance-based stability criterion for grid-connected inverters[J].IEEE Transactions on Power Electronics,2011,26（11）:3075-3078.

[6]Ghanem A,Rashed M,Sumner M,et al.Grid impedance estimation for islanding detection and adaptive control of converters[J].IET Power Electronics,2017,10（11）:1279-1288.

[7]Cobreces S,Bueno E J,Pizarro D,et al.Grid impedance monitoring system for distributed power generation electronic interfaces[J].IEEE Transactions on Instrumentation and Measurement,2009,58（9）:3112-3121.

[8]谢少军,季林,许津铭.并网逆变器电网阻抗检测技术综述[J].电网技术,2015,39（2）:320-326.Xie Shaojun,Ji Lin,Xu Jinming.Review of grid impedance estimation for gird-connected inverter[C].Power System Technology,2015,39（2）:320-326（in Chinese）.

[9]汤婷婷,张兴,谢东,等.基于高频注入阻抗检测的孤岛检测研究[J].电力电子技术,2013,47（3）:70-72.Tang Tingting,Zhang Xing,Xie Dong,et al.Islanding detection method based on impedance detection using high frequency signal injection[J].Power Electronics,2013,47（3）:70-72（in Chinese）.

[10]Asiminoaei L,Teodorescu R,Blaabjerg F,et al.Implementation and test of an online embedded grid impedance estimation technique for PV inverters[J].IEEE Transactions on Industrial Electronics,2005,52（4）:1136-1144.

[11]Ciobotaru M,Teodorescu R,Blaabjerg F.On-line grid impedance estimation based on harmonic injection for gridconnected PV inverter[C].2007 IEEE Interna tional Symposium on Industrial Electronics.Vigo,Spain,2007:2437-2442.

[12]吴学智,梁建钢,童亦斌,等.基于复数滤波器和非特征次谐波注入的电网阻抗估算方法[J].电网技术,2013,37（10）:2796-2801.Wu Xuezhi,Liang Jiangang,Tong Yibin,et al.Research on method of grid impedance estimation by complex filters based initiative harmonic injection[C].Power System Technology,2013,37（10）:2796-2801（in Chinese）.

[13]吕洋,徐政.投切电容器时的电网谐波阻抗测量方法[J].高电压技术,2009,35（7）:1780-1784.Lyu Yang,Xu Zheng.Network harmonic impedance measurement using capacitor switching[J].High Voltage Engineering,2009,35（7）:1780-1784（in Chinese）.

[14]沈永波,年珩.不平衡及谐波电网下基于静止坐标系的并网逆变器直接功率控制[J].电工技术学报,2016,31（4）:114-123.Shen Yongbo,Nian Heng.Stationary frame direct power control of grid-connected inverter under unbalanced and harmonic grid voltage[J].Transactions of China Electrotechnical Society,2016,31（4）:114-123（in Chinese）.

[15]Li Weiwei,Ruan Xinbo,Bao Chenlei,et al.Grid synchronization systems of three-phase grid-connected power converters:A complex-vector-filter perspective[J].IEEE Transactions on Industrial Electronics,2014,61（4）:1855-1870.

[16]Golestan S,Monfared M,Freijedo F D,et al.Performance improvement of a prefiltered synchronous-reference-frame PLL by using a PID-type loop filter[J].IEEE Transactions on Industrial Electronics,2014,61（7）:3469-3479.

[17]胡寿松.自动控制原理[M].第4版.北京:科学出版社,2001.