A hybrid algorithm based on ILP and genetic algorithm for time-aware test case prioritization

Sun Jiaze　Wang Gang

(1School of Computer Science and Technology, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)(2Shaanxi Key Laboratory of Network Data Intelligent Processing, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

Regression testing is costly in software evolution, which consumes 80% of the overall testing budgets[1].Test case prioritization (TCP)is an efficient and practical regression testing technique, and it can be used to reorder the test cases to achieve the goal of improving the test efficiency and reducing the test cost.Over the past few years, many test case prioritization techniques have been proposed to study various prioritization approaches[2-4]and coverage criteria[5].However, these approaches do not definitely consider the time budget and the execution time difference of test cases.Executing the entire test suite is sometimes time-consuming, which does not allow for the execution of all the test cases.Therefore, the test cases are usually executed under time constraints.

Many researchers have focused on time-aware test case prioritization.Walcott et al.[6]reduced time-aware test case prioritization to the zero/one knapsack problem,and used the genetic algorithm to solve the problem.Zhang et al.[7]selected a subset of original test suites by integer linear programming (ILP), and prioritized the selected test cases by traditional total prioritization and additional prioritization.You et al.[8]used the SIEMENS suite and space program as empirical research objects to prioritize test suites by random ordering, total strategy, additional strategy, ILP-total, and ILP-additional, respectively.Do et al.[9]found that the best effective TCP technology under a certain time constraint cannot ensure the best effect under other time constraints.Recently, Hao et al.[3]presented a unified test case prioritization approach that encompassed both the total and additional strategies.Lu et al.[10]found that the genetic algorithm can obtain better results than other techniques, such as random, total, additional, and search-based techniques.

As the above literature shows, greedy strategy and random ordering are not always effective under different time constraints.The convergence speed of the genetic algorithm is not fast, and the initial value of TCP is sensitive.The test case selection involves a subset which is selected from the original test suite.Broadly speaking, it is related to the research on regression test case selection[11]and test case reduction[12].Meanwhile, ILP is an effective optimization method for the zero/one knapsack problem[7].Therefore, this paper uses ILP for the test case selection and the genetic algorithms for prioritizing the selected test cases.We compare ILP-GA with two greedy-based approaches under different time constraints, and the experimental results show that our approach is superior to greedy-based approaches.In summary, the paper makes the following contributions: It is the first attempt to combine ILP and genetic algorithms for time-aware test case prioritization, and the empirical evaluation of the proposed approach and approaches of the greedy strategy based ILP is carried out in detail; the time complexity of ILP-GA is analyzed.

1　Time-Aware Test-Case Prioritization

Time-aware test case prioritization is usually formalized as follows.

Given: A test suite,S; the set of permutations of all subsets ofS,P; objective functionFand time cost functionT, which range from permutations to real numbers;time constraint,tmax.

Problem: Time-aware test case prioritization aims to find a permutationS′∈Psatisfying that for any elementS″∈P(S″≠S′),F(S′)≥F(S″),T(S″)≤tmax, andT(S′)≤tmax.

In the problem,Pis the set of all possible ordering ofS;Tis a function, and it yields the execution time of that ordering when it is applied to any ordering ofS, so we can decide whether an ordering satisfies the time constraint through judging the inequalityT(S′)≤tmax; the functionFis applied to any ordering and returns a fitness value of that ordering.In this paper, the functionFmeasures a test sequence’s ability of detecting bugs as early as possible, and we stipulate that a test sequence with a higher fitness value is superior to that with a lower fitness value.

2　Proposed Approach

In this paper, we propose a new approach for time-aware test case prioritization by combining integer linear programming and the genetic algorithm.As shown in Fig.1, our approach is composed of two steps.First, we use the ILP model to select a subset of original test suites which satisfies the time constraint.Secondly, we prioritize the subset by the genetic algorithm.

Fig.1　The description of ILP-GA

We consider branch coverage criteria and method coverage criteria in this paper.For the ease of presentation, we present our approach only in terms of branch coverage.

2.1　Test case selection

Test case selection can be formalized as two ILP models, and each model is composed of decision variables, an objective function and a constraint system.As shown in Fig.2, we denote the original test suite asSand two subsets of the original test suite are denoted asS1andS2, respectively.S1satisfies the time constraint and maximizes the number of covered branches, and it is selected by the first ILP model.We denote the sum of time ofS1ast1, so the remaining time from the time constraint istmax-t1.Furthermore,S2will be selected by the second ILP model.S2has the maximum sum of the number of branches covered by each test case that belongs toS3(S3=S-S1)and the total time ofS2does not exceedtmax-t1.Thus, after solving the two ILP models, all the test cases that have been selected can be denoted asS′(S′=S1∪S2), and we denote the number of these test cases asn.The first ILP model will be built as follows.

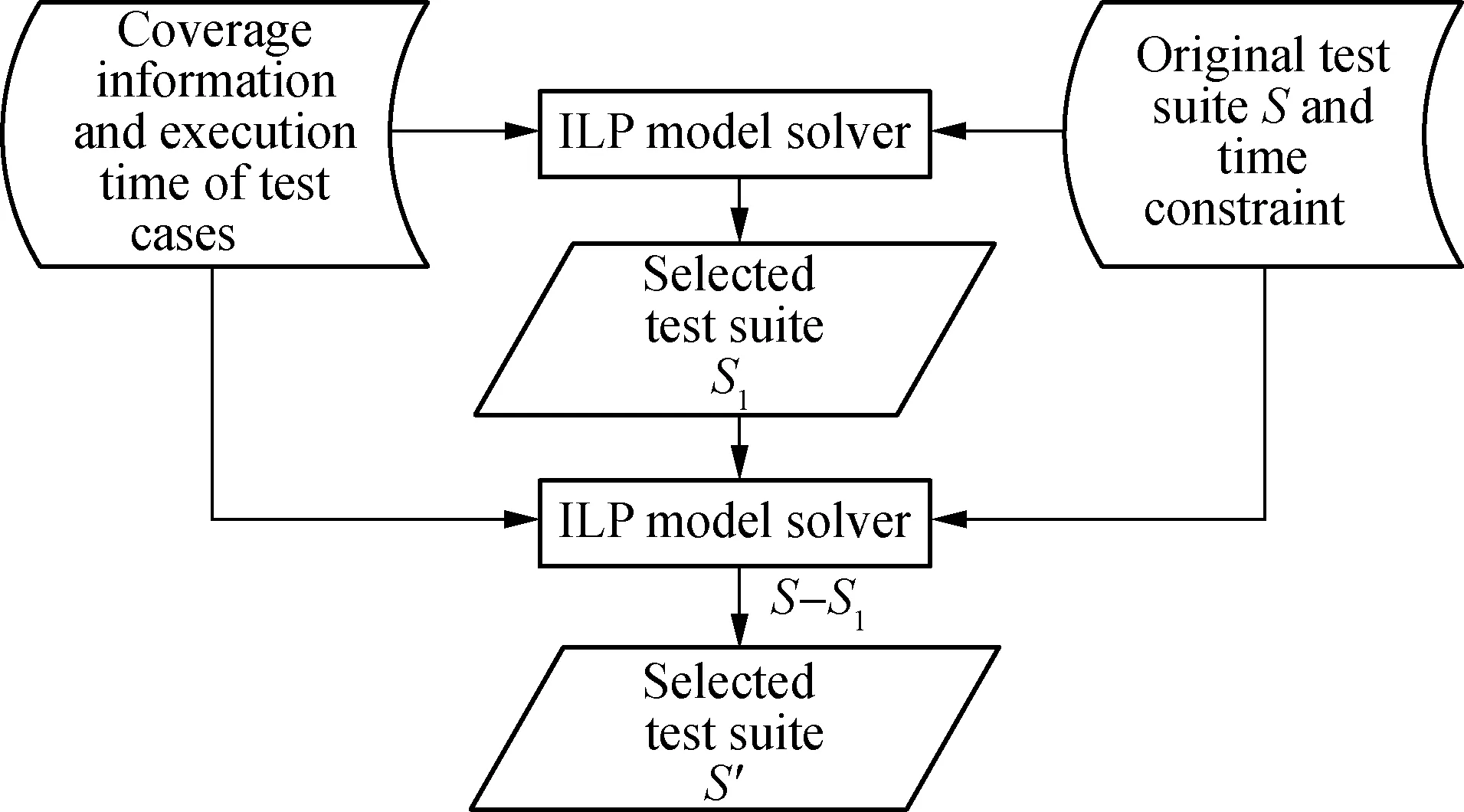
Fig.2　The technological process of ILP

2.1.1Decision variables

For each test case, there is a Boolean decision variable to represent whether the test case is selected or not.The test suite is denoted asS={s1,s2,…,sn}, andnBoolean decision variables are denoted asxi(1≤i≤n).xiis defined as

(1)

Furthermore, there is another group of Boolean decision variables to represent whether each branch is covered by one or more test cases.A set of branches are denoted asBR={b1,b2,…,bm}, andyiis defined as

(2)

2.1.2Objective function

Our goal of test case selection is to maximize the number of covered branches, so the objective function can be defined as

(3)

In the objective function, if any selected test case does not coverbj, the valueyjis 0.Thus, Eq.(3)guarantees to count each covered branch just once.

2.1.3Constraint system

To ensure that the selected test cases satisfy the time constraint, an inequality is defined as

(4)

Formula (4)indicates that the sum of execution time of all the selected test cases is no more thantmax.Furthermore, there is a group of inequalities to ensure that, ifyj=1(1≤j≤m), at least one test case coveringbjis selected.There is a need to represent whether a test case covers a branch, and it can be denoted as

(5)

Using the coverage information in Eq.(5), the inequalities can be defined as

(6)

2.1.4Further test case selection

A subset of test cases that can satisfy the time constraint and maximize the number of branches has been selected by the first ILP model, but there may be some time left over from time budget, so the second ILP model will be built for later selecting test cases to enhance the fault detection in the time constraint.It is noted that further selecting does not necessarily increase the number of covered branches, but these test cases may contribute to detecting faults.

The unselected test cases inSare denoted asC(C={c1,c2,…,cL})and time left fromtmaxis denoted astleft.TheLBoolean decision variables are denoted byzk(1≤k≤L), andzkis defined as

(7)

The objective function shows that a subset of test suite that has the maximum sum of the number of branches covered by each test case should be selected fromC, and it is defined as

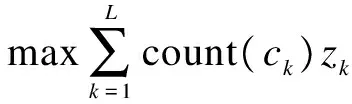
(8)

The constraint system indicates that the sum of execution time of all the selected test cases fromCis no more thantleft, and it is defined as

(9)

2.2　Test case prioritization

After the test case selection, the time-aware test case prioritization is transformed into the traditional test case prioritization.Test case prioritization is a NP-complete problem.The genetic algorithm is a heuristic search algorithm which provides a general framework for solving complex problems.The genetic algorithm is used to prioritize test cases, as described in Algorithm 1.It should be noted that the cover matrixAis used to record the coverage information of program entities of a program.If thej-th program entity is covered by thei-th test case, thenaij=1, otherwiseaij=0.

Algorithm1Genetic algorithm

Input: Test suiteS; the number of initial sequences of test casesN; the maximum number of iterationsgmax; crossover probabilityPc; mutation probabilityPm; coverage information of program entitiesMc; the execution time of test cases inS,TS.

Output: A test sequence with the highest fitness valueσmax.

1.R0∈∅

2.repeat

3.R0←R0∪{InitializeRandomPopulation(S,Mc)}

4.until |R0|=N

5.g←0

6.repeat

7.F←∅

8.forσi∈Rg

9.F←F∪{computeFitness(σi,Mc,TS)}

10.σ1,σ2←EliteTwoBest(Rg,F)

11.Rg+1←σ1,σ2

12.repeat

13.σj,σk←Select(Rg-{σ1,σ2},F)

14.σq,σr←Crossover(Pc,σj,σk)

18.until |Rg+1|=N

19.g←g+1

20.untilg>gmax

21.σmax←FindMaxFitnessSequence(Rg-1,F)

22.returnσmax

2.2.1Genetic algorithm framework

We denote the subsetS′ in section 2.1 asS.All of probabilitiesPc,Pm∈[0,1].In general, anyσi∈perms(2S)has the formσi=〈Sj,…,Sn〉, andnis the number of test cases inσi.perms(2S)represents the set of all possible sequences and subsequence ofT.A test sequence is composed ofnnumbers and we denote a test sequence as 〈w1,…,wi,wi+1,…,wn〉 (1≤wi≤nandwi≠wi+1).A test sequence is an integer array and there is a numberwiin each position of the integer array.

As shown in Algorithm 1, in the loop beginning on line 3, the algorithm creates a setR0containingNrandom test sequencesσifrom perms(2S).R0is the first generation in the iteration.If a test sequence is created, then computeFitness(σi,Mc,TS)will be used to compute the fitness of this test sequence.We denoteFias the fitness value ofσi.We also useF=〈F1,F2,…,FN〉 to denote the sequence of fitness for eachσi∈Rg,0≤g≤gmax.

The EliteTwoBest(Rg,F)on line 10 chooses the two best test sequences inRgto be elements for the next generationRg+1, which applies the elitist selection technique.On line 13, Select(Rg-{σ1,σ2},F)identifies pairs of sequences {σj,σk} fromRgthrough a roulette wheel selection technique.The Crossover(Pc,σj,σk)on line 14 may form two new test sequences {σq,σr} based onPc.Each test sequence in the pair {σq,σr} may then be mutated based onPm.

After each of these operations has been executed, bothσqandσrare set intoRg+1, as seen on line 17.The same transformations are applied to all pairs selected by Select(Rg-{σ1,σ2},F)untilRg+1containsNtest sequences.In total,gmaxsets ofNtest sequences are iteratively created as described in Algorithm 1 on lines 6 to 20.When the final setRgmaxhas been created, the test sequence with the greatest fitness,σmax, is determined on line 21.

2.2.2Fitness function

computeFitness(σi,Mc,TS)on line 9 usesF(σi,Mc,TS)to calculate the fitness value.The fitness function, represented byF(σi,Mc,TS), assigns each test sequence a fitness value based on the program entity coverage (P)of that sequence and the execution time of each test case(T(〈Sj〉)).

F(σi,Mc,TS)is computed by summing the products of execution timeT(〈Sj〉)and thePof the subsequenceσi{1,j}=〈S1,S2,…,Sj〉 for each test caseSj∈σi.TheF(σi,Mc,TS)gives precedence to test sequences that have more codes covered early in execution.Formally, for someσi∈perms(2S),

(10)

2.2.3Selection operation

2.2.4Crossover operation

As explained in section 2.2.1, pairs of test sequences are selected fromRg.Crossover(Pc,σj,σk)performs crossover operation and creates two new test sequences from{σj,σk}.A random numberr1∈[0,1)is generated, and the crossover operator is executed whenPcis greater thanr1.When the crossover begins, another random numberk∈[0,n)is generated as the crossover point, andnis the number of test cases inS.The firstknumbers inσjare copied to the firstkpositions inσq.Let us denote the numbers which are in theσkand which is not equal to the firstknumbers in theσjasnw1, and then we use each number innw1to fillσqone by one into the last (n-k)positions inσq.Thus, a new test sequenceσqis generated by the above steps.Analogously,σris also generated as the same steps.Finally, we obtain the two new test sequences {σq,σr} by crossover operation.

2.2.5Mutation

Mutation(Pm,σq)is used to mutateσq.First, a random numberr3∈[0,1)is generated.IfPmis greater thanr3, the mutation operation is executed.If mutation is to occur, the two positions will be selected fromσqand the two test cases which are in the two positions will be swapped.Mutation(Pm,σr)is used to mutateσr, and it is similar to Mutation(Pm,σq).

2.3　Analysis of algorithm

First, we analyze the time complexity of the genetic algorithm as follows.We denote the number of test cases asn1and the number of program entities of a program asn2.The time complexity of reading coverage information from I/O isO(n1n2).The time complexity of the reading execution time of test cases from I/O isO(n1).The time complexity of initializing population isO(n1N).The time complexity of computing fitness values for all test sequences isO(n1n2N).The time complexity of elite strategy isO(N2).We use roulette wheel selection technique and bubble sort in selection operation, so the time complexity of selection operation isO(n1n2N)+O(N2)N/2.The time complexity of crossover selection isO(n1N).The time complexity of the mutation operation isO(N).Therefore, the time complexity of the genetic algorithm isO(n1n2N)+O(n1N)+O(N2).The calculation of fitness values and genetic operators is main time overhead, and the number of calling the genetic algorithm determines the efficiency of the algorithm.

Secondly, if we denote the number of decision variables asnand the number of constraint conditions asm, then the time complexity of ILP isO(mn).Furthermore,n=n1+n2approximately andm=n2approximately, so the time complexity of ILP isO(n2(n1+n2)).

In summary, the time complexity of ILP-GA isO(n1n2N)+O(n1N)+O(N2)+O(n2(n1+n2)).The time complexity of ILP-GA is determined byn1,n2andN.The ILP-GA is a polynomial algorithm.

3　Empirical Evaluation

We implemented the approach described in Section 2 and measured its effectiveness and stability.

3.1　Experimental setup

In the experiments, we used five classical open sources Java projects[10]from GitHub, which had been widely used in software testing research, and they are described in Tab.1.All experiments were performed on Windows 764 bit, a 3.60 GHz Intel Core 3 processor and 8 GB of main memory.The ILP-total and ILP-additional were implemented in the Python language.The genetic algorithm was implemented in the Java language based on JDK 1.7.0.We ran these algorithms in Eclipse 4.3.To implement the ILP-based techniques (i.e., total & additional test prioritization via ILP), we used a mathematical programming solver, GUROBI Optimization (http://www.gurobi.com), which was used to represent and solve the equations formulated by the ILP-based techniques.The number of initial orderings of test cases is 60.We adopt the same parameters in Ref.[6] to compare the experimental results with the classical result.The number of iterations for the GA is 25.The crossover probability and mutation probability are 0.70 and 0.10, respectively.

Tab.1Experimental subjects

SubjectThenumberofbranchesThenumberofmethodsThenumberoftestcasesThewebsiteofprojectJasmine⁃maven9513824https：//github．com/searls/jasmine⁃maven⁃pluginJava⁃apns8212847https：//github．com/notnoop/java⁃apnsLa4j967536245https：//github．com/vkostyukov/la4jMetrics⁃core460695129https：//github．com/nablex/metrics⁃coreScribe⁃java6217351https：//github．com/Kailashrb/scribe⁃java

3.2　Experiments and results

3.2.1Effectiveness for different techniques

ILP-total, ILP-additional and ILP-GA were used to solve time-aware test case prioritization in our experiments, and we compared them by effectiveness and stability.We used 25% and 75% as the two different time constraints.The branch and method are used as test adequacy criteria.As shown in Tab.2, each project was applied by three approaches under different time constraints and different test adequacy criteria, so each project will have four different comparison methods by three approaches.For each comparison method, we ran three algorithms 20 times, then calculated the average value of 20 fitness values of each algorithm.The prioritization efficiency of the ILP-GA is improved on average by approximately 54% and 13%, respectively, under 25% time constraints and it is improved on average by, approximately, 42% under 75% time constraints, so we conclude that our technique is effective.It should be noted that the branch coverage of the last two projects have a close average fitness value under 25% time constraint, and we speculate that the two average fitness values are close to optimal solutions.

Tab.2Experimental results of three algorithms

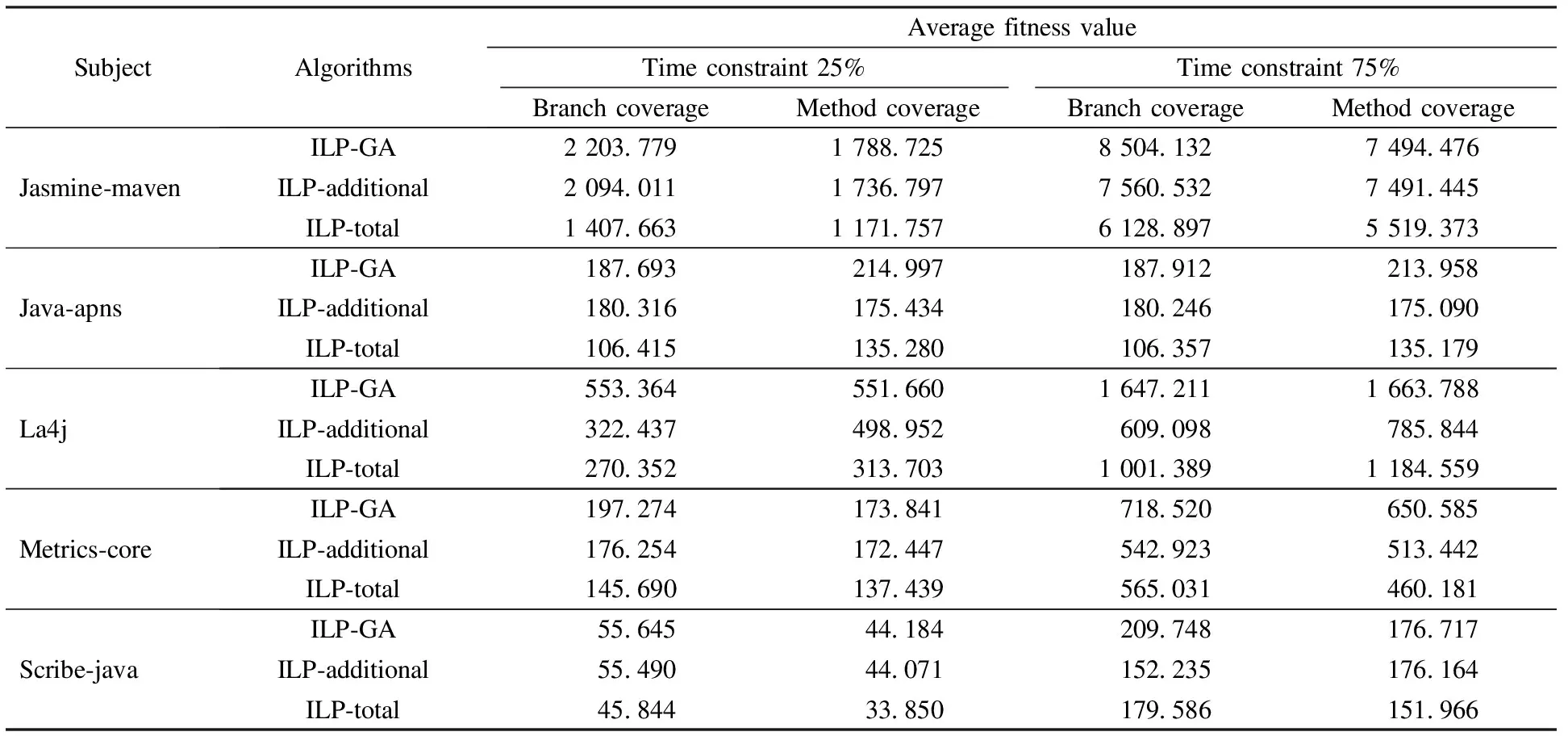
SubjectAlgorithmsAveragefitnessvalueTimeconstraint25%Timeconstraint75%BranchcoverageMethodcoverageBranchcoverageMethodcoverageJasmine⁃mavenILP⁃GA2203 7791788 7258504 1327494 476ILP⁃additional2094 0111736 7977560 5327491 445ILP⁃total1407 6631171 7576128 8975519 373Java⁃apnsILP⁃GA187 693214 997187 912213 958ILP⁃additional180 316175 434180 246175 090ILP⁃total106 415135 280106 357135 179La4jILP⁃GA553 364551 6601647 2111663 788ILP⁃additional322 437498 952609 098785 844ILP⁃total270 352313 7031001 3891184 559Metrics⁃coreILP⁃GA197 274173 841718 520650 585ILP⁃additional176 254172 447542 923513 442ILP⁃total145 690137 439565 031460 181Scribe⁃javaILP⁃GA55 64544 184209 748176 717ILP⁃additional55 49044 071152 235176 164ILP⁃total45 84433 850179 586151 966

3.2.2Stability for different techniques

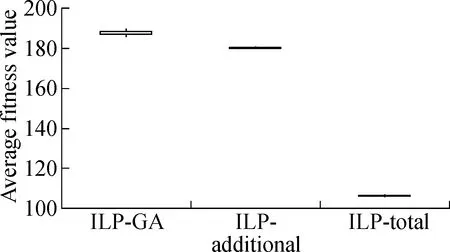
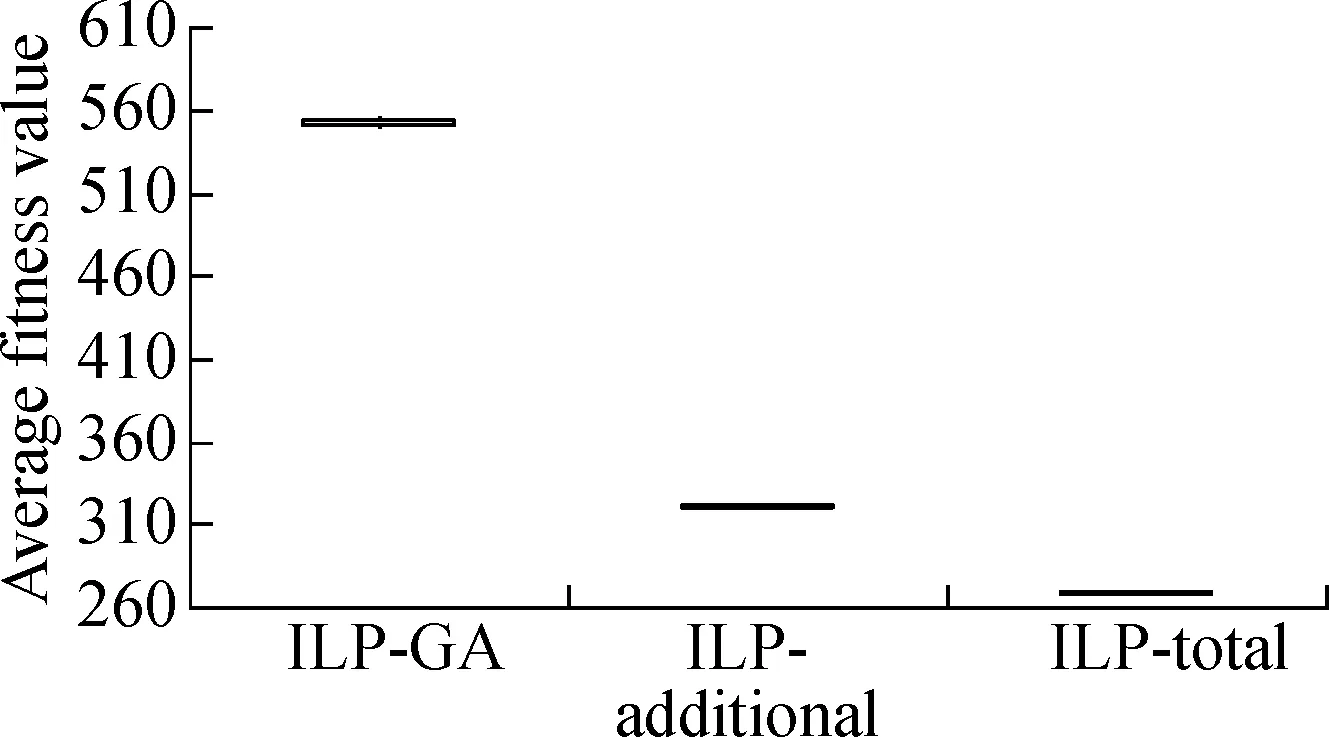
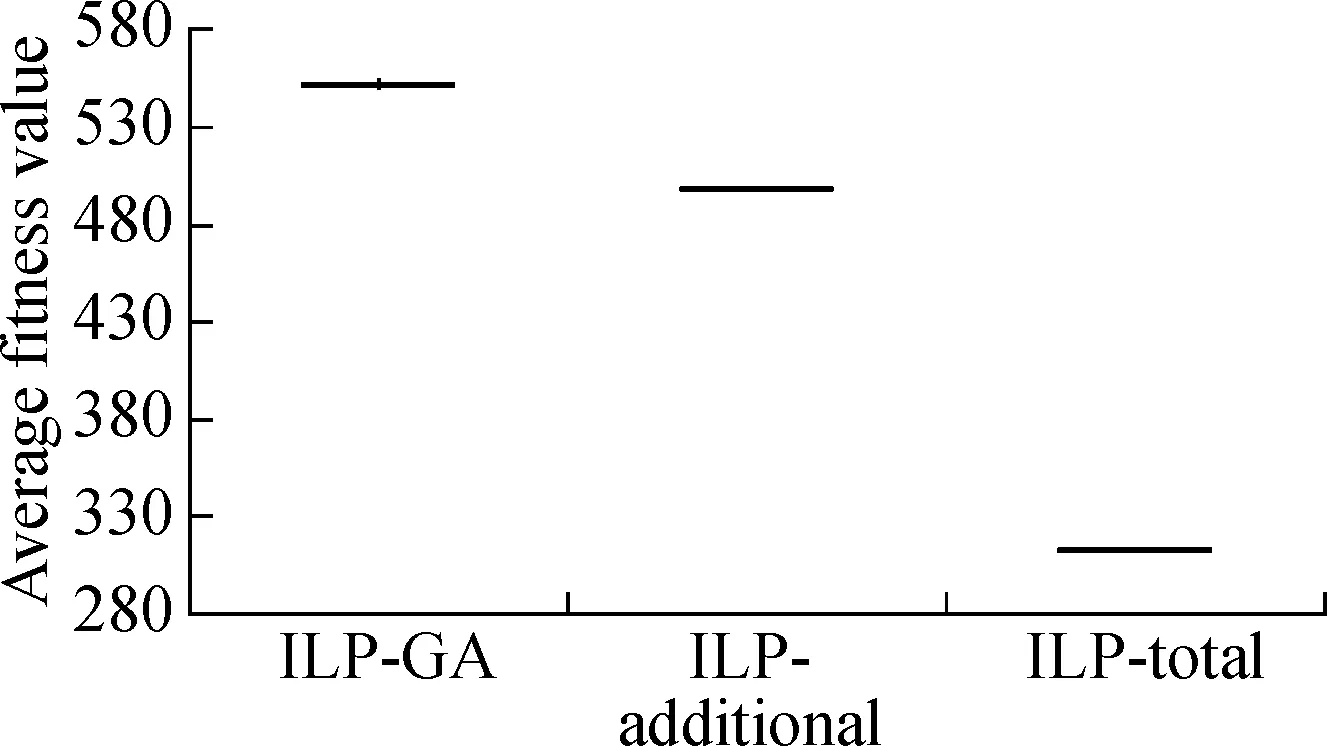
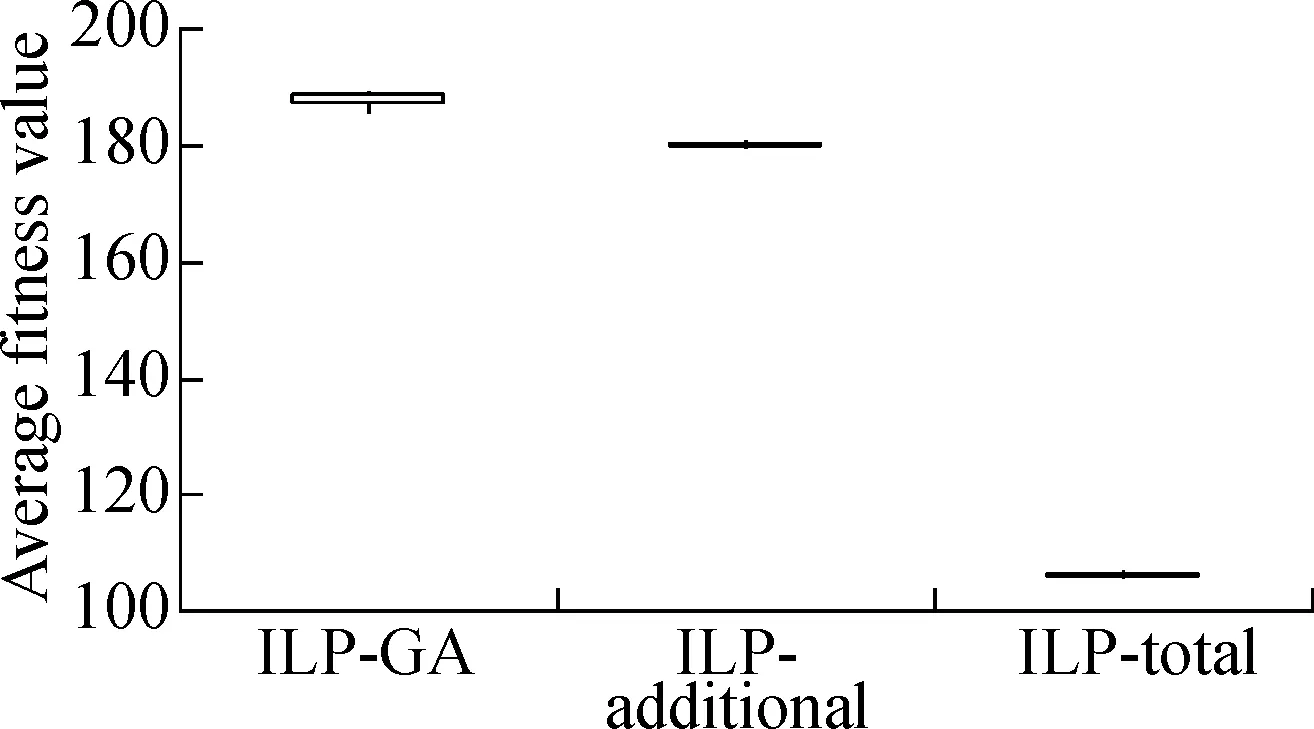
The boxplots in Fig.3 and Fig.4 depict the results of the three approaches under two different time constraints.We have the following observations.First, whether the time constraint is 25% or 75%, the results of ILP-GA are overall superior to the ILP-total and ILP-additional for Java-apns and La4j.Secondly, we consider the distribution of results which is generated by each approach.As can be seen from Fig.3 and Fig.4, the height of each box is small.The fitness values in the box are close and concentrated.Thus, all the approaches perform stably.In short, no matter what the time constraint is and what the test adequacy criterion is, our approach always achieves the expected effectiveness and stability.

(a)

(b)

(c)

(d)

Fig.3Box-plots of result contrast of ILP-GA, ILP-additional and ILP-total under 25% time constraint.

(a)Branch coverage of Java-apns; (b)Branch coverage of La4j; (c)Method coverage of Java-apns; (d)Method coverage of La4j

(a)

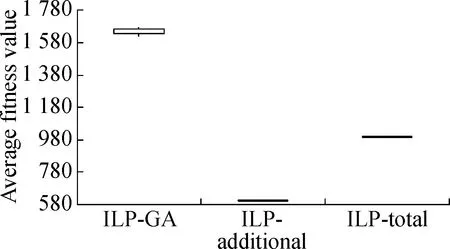
(b)

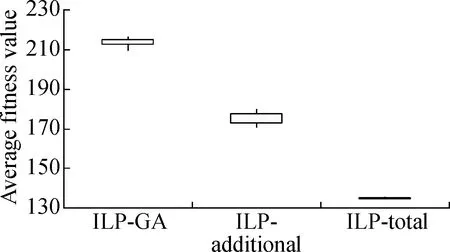
(c)

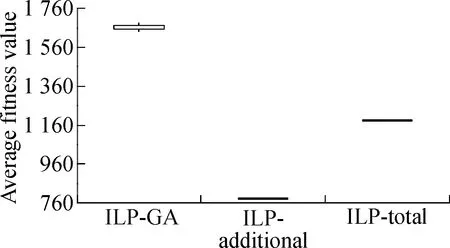
(d)

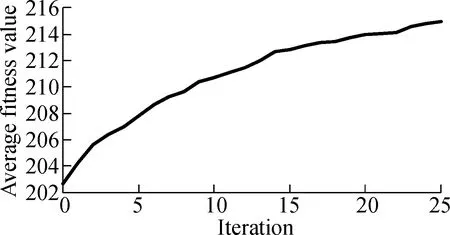
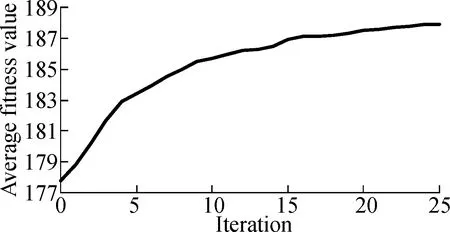
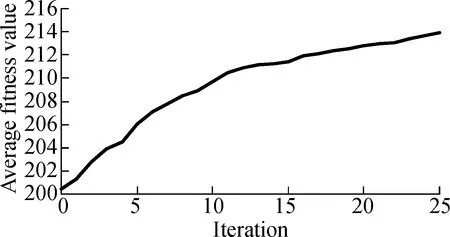
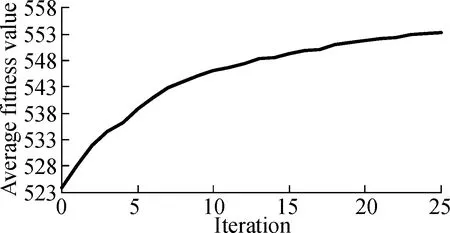
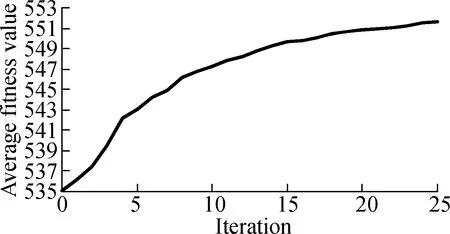
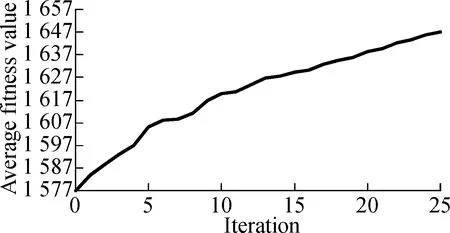
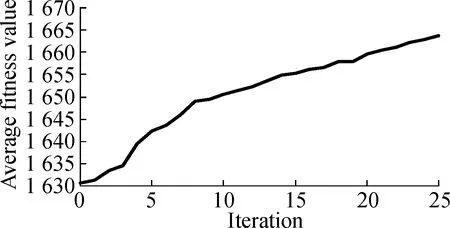
3.2.3Convergence for ILP-GA

Fig.5 and Fig.6 describe the change of the average fitness value along with iterations for three projects under two time constraints.As can be seen from Fig.5 and Fig.6, the average fitness values improve along with iterations.It also can be seen that the rise of curves is a near-linear trend in the former iterations and curves become less steep in the last several iterations.Therefore, the convergence rate of ILP-GA is fast, and our experimental results are close to the global optimal solutions.

4　Conclusions

1)Considering the rate of coverage, our approach outperforms the ILP-additional and ILP-total under different time constraints.

2)Considering stability and convergence, our approach has good stability and a fast convergence rate.

3)When the time constraint is not tight, our approach is superior to other techniques, but ILP-additional can perform competitively when time constraint is tight.

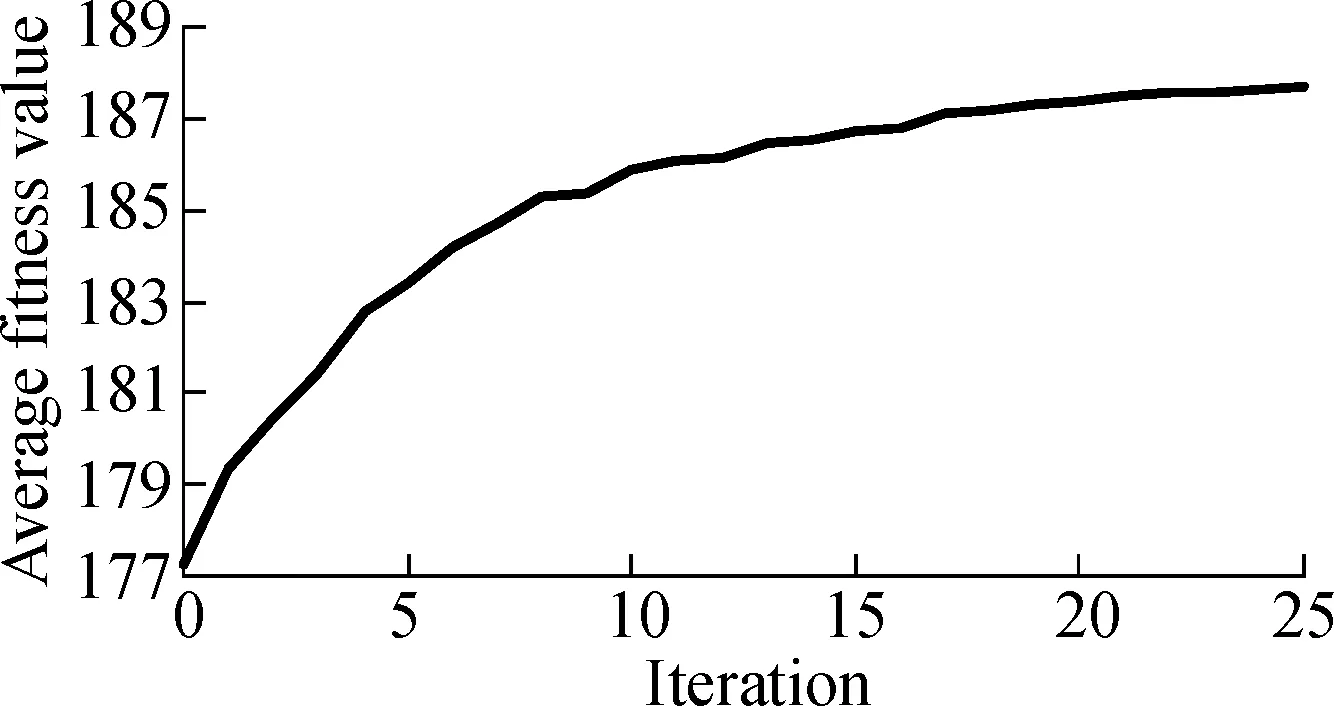
(a)

(b)

(c)

(d)

(a)

(b)

(c)

(d)

In future work, we intend to explore the following several aspects.First, we intend to study new algorithms and new evaluation indices to improve the effectiveness of prioritization.Secondly, we plan to implement a prototype tool to complete the whole test case optimization process from the information collection to the result visualization.

[1]Chittimalli P K, Harrold M J.Recomputing cover age information to assist regression testing [J].IEEETransactionsonSoftwareEngineering, 2009,35(4):452-469.DOI:10.1109/TSE.2009.4.

[2]Li Z, Harman M, Hierons R M.Search algorithms for regression test case prioritization [J].IEEETransactionsonSoftwareEngineering, 2007,33(4):225-237.DOI: 10.1109/TSE.2007.38.

[3]Hao D, Zhang L M, Zhang L, et al.A unified test case prioritization approach [J].ACMTransactionsonSoftwareEngineeringandMethodology, 2014,24(2):1-31.DOI:10.1145/2685614.

[4]Luo Q, Moran K, Poshyvanyk D.A large-scale empirical comparison of static and dynamic test case prioritization techniques[J].Proceedingsofthe2016 24thACMSIGSOFTInternationalSymposiumonFoundationsofSoftwareEngineering.Seattle, WA, USA,2016: 559-570.DOI:10.1145/2950290.2950344.

[5]Mei H, Hao D, Zhang L M, et al.A static approach to prioritizing junit test cases [J].IEEETransactionsonSoftwareEngineering, 2012,38(6):1258-1275.DOI: 10.1109/TSE.2011.106.

[6]Walcott K R, Soffa M L, Kapfhammer G M, et al.Time aware test suite prioritization [C]//Proceedingsofthe2006InternationalSymposiumonSoftwareTestingandAnalysis.Portland, Maine, USA, 2006: 1-11.DOI:10.1145/1146238.1146240.

[7]Zhang L, Hou S S, Guo C, et al.Time-aware test case prioritization using integer linear programming[C]//ProceedingsoftheEighteenthInternationalSymposiumonSoftwareTestingandAnalysis.Chicago, IL, USA, 2009: 213-224.DOI:10.1145/1572272.1572297.

[8]You D J, Chen Z Y, Xu B W, et al.An empirical study on the effectiveness of time-aware test case prioritization techniques [C]//Proceedingsofthe26thACMSymposiumonAppliedComputing.Taichung, China, 2011: 1451-1456.DOI:10.1145/1982185.1982497.

[9]Do H, Mirarab S, Tahvildari L, et al.The effects of time constraints on test case prioritization: A series of controlled experiments [J].IEEETransactionsonSoftwareEngineering, 2010,36(5):593-617.DOI:10.1109/TSE.2010.58.

[10]Lu Y F, Lou Y L, Cheng S Y, et al.How does regression test prioritization perform in real-world software evolution [C]//Proceedingsofthe38thInternationalConferenceonSoftwareEngineering.Austin, TX, USA,2016:535-546.DOI:10.1145/2884781.2884874.

[11]Yoo S, Harman M.Regression testing minimization, selection and prioritization: A survey [J].SoftwareTesting,VerificationandReliability, 2012,22(2):67-120.DOI:10.1002/stvr.430.

[12]Alipour M A, Shi A, Gopinath R, et al.Evaluating non-adequate test case reduction [C]//Proceedingsofthe31stIEEE/ACMInternationalConferenceonAutomatedSoftwareEngineering.Singapore, 2016: 16-26.DOI:10.1145/2970276.2970361.