Generalized Cayley-Hamilton theoremfor core-EP inverse matrix and DMP inverse matrix

Wang Hongxing　Chen Jianlong　Yan Guanjie

(1School of Mathematics, Southeast University, Nanjing 211189, China)(2School of Science, Guangxi University for Nationalities, Nanning 530006, China)

In this paper, we use the following notations.The symbolCm,nis the set ofm×nmatrices with complex entries, and rk(A)represents the rank ofA∈Cm,n.LetA∈Cn,n, and then the smallest non-negative integerk, which satisfies rk(Ak+1)=rk(Ak), is called the index ofAand is denoted as Ind(A).The Moore-Penrose inverse ofA∈Cm,nis defined as the unique matrixX∈Cn,msatisfying the equationsAXA=A,XAX=X, (AX)*=AX, (XA)*=XA, and is denoted asX=A+.The Drazin inverse ofA∈Cn,nis defined as the unique matrixX∈Cn,nsatisfying the equationsXAk+1=Ak,XAX=X,AX=XAand is usually denoted asX=AD(see Ref.[1]).The core-EP inverse ofA∈Cn,nis defined as the unique matrixX∈Cn,nsatisfying the equationsXAk+1=Ak,XAX=Xand (AX)*=AX, and is denoted asX=A⨁[2].The DMP inverse ofA∈Cn,nis defined as the unique matrixX∈Cn,nsatisfying the equationsXAX=X,XA=ADAandAmX=AkA+, and is denoted asX=Ad,+[3].More details of the Drazin, core-EP, DMP inverses can be seen in Refs.[4-8].

The Cayley-Hamilton theorem has many applications in nonlinear time-varying systems, electric circuits, etc.The classical Cayley-Hamilton theorem was extended to the fractional continuous-time and discrete-time linear systems[9], nonlinear time-varying systems with square and rectangular systems[10], the Drazin inverse matrix and standard inverse matrix[11], etc.More details about the Cayley-Hamilton theorem and its applications can be read in Refs.[9-13].Therefore, it is very interesting to investigate the Cayley-Hamilton theorem for the core-EP inverse matrix and DMP inverse matrix.In this paper, our main tools are core-EP decomposition and generalized inverses.

1　Preliminaries

In this section, we present some preliminary results.

Theorem1[14, Cayley-Hamilton theorem]LetpA(s)=det(sEn-A)be the characteristic polynomial ofX∈Cn,n.ThenpA(A)=0.

Theorem2[14]LetA∈Cn,nis singular, i.e.det(A)=0, and the characteristic polynomial ofAbe

pA(s)=det(sEn-A)=sn+an-1sn-1+…+a1s

(1)

Then

fA(AD)=a1(AD)n+a2(AD)n-1+…+an-1(AD)2+AD=0

(2)

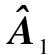
(3)

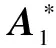
(4)

whereT∈Crk(A),rk(A)is non-singular,Nis nilpotent andNk=0.

Lemma3Let the core-EP decomposition ofA∈Cn,nbe as in Lemma 2.Then the core-EP inverse ofAis

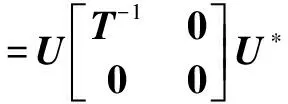
(5)

Let the core-EP decomposition ofAbe as in (4).Then

(6)

and

(7)

2　Main Results

In this section the classical Cayley-Hamilton theorem will be extended to the core-EP inverse matrix and DMP inverse matrix.By assumption, matrixAis singular, i.e.det(A)=0.

Lemma4Let the characteristic polynomial ofA∈Cn,nbe as in Eq.(1).Then

fA(A⨁)=a1(A⨁)n+a2(A⨁)n-1+…+

an-1(A⨁)2+A⨁=0

(8)

ProofUsing (1)and Theorem 1 we obtain

An+an-1An-1+…+a1A=0

(9)

It follows from Lemma 2 and (6)that

(10)

Post-multiplying (10)by

we have

(11)

Therefore, by applying (7), we obtain (8).

Example1Let

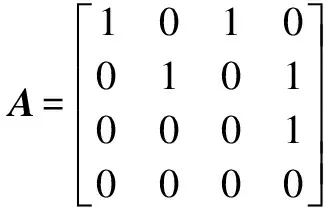
Then Ind (A)=2, the DrazinADis

and the core-EP inverseA⊕is

The characteristic polynomial ofAis

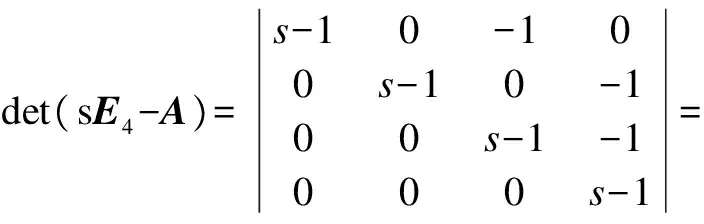
From the classical Cayley-Hamilton theorem, we haveA4-2A3+A2=0.By applying Lemma 4, we obtain (A⊕)3-2(A⊕)2+A⊕=0.

Note that, if the characteristic polynomials ofA⨁andADis

pA⨁(s)=det(sEn-A⨁)=sn+bn-1sn-1+…+b1s

(12)

pAD(s)=det(sEn-AD)=sn+cn-1sn-1+…+c1s

(13)

respectively, we cannot obtain

pA⨁(s)=b1An+b2An-1+…+bn-1A2+A

(14)

pAD(s)=c1An+c2An-1+…+cn-1A2+A

(15)

Example2Let

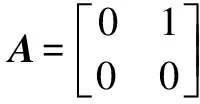
It is easy to confirm that the core-EP inverseA⊕is

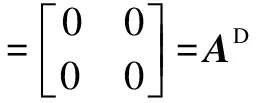
Then

but

fAD(s)=fA⊕(s)=0A2+A=A≠0

Theorem3LetA∈Cn,nand Ind(A)=k.Then the characteristic polynomial ofA⨁∈Cn,nis

pA⨁(s)=sn+bn-1sn-1+…+bn-rk(Ak)sn-rk(Ak)

(16)

Furthermore,

bn-rk(Ak)An+…+bn-1An-rk(Ak)+1+An-rk(Ak)=0

(17)

ProofLet the core-EP decomposition ofA, i.e.A=A1+A2, be as in Lemma 2.Then

sn-rk(Ak)det(sErk(Ak)-T-1)

Therefore, we obtain (16).Using (16)and Theorem 1, we obtain

(A⨁)n+bn-1(A⨁)n-1+…+bn-rk(Ak)(A⨁)n-rk(Ak)=0

(18)

that is,

(19)

Post-multiplying (19)by

we have (17).

Theorem4LetA∈Cn,n, Ind(A)≤1 and the characteristic polynomial ofA⨁∈Cn,nbe as in (12).Then

fA⨁(A)=b1An+b2An-1+…+bn-1A2+A=0

(20)

Theorem5LetA∈Cn,nand Ind(A)=k.Then the characteristic polynomial ofAD∈Cn,nis

pAD(s)=det(sEn-AD)=sn+cn-1sn-1+…+cn-rk(Ak)sn-rk(Ak)

(21)

Furthermore,

cn-rk(Ak)An+…+cn-1An-rk(Ak)+1+An-rk(Ak)=0

(22)

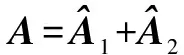
sn-rk(Ak)det(sErk(Ak)-Σ-1)

Therefore, we obtain (21).Using (21)and Theorem 1 we obtain

(AD)n+bn-1(AD)n-1+…+bn-rk(Ak)(AD)n-rk(Ak)=0

that is,

Post-multiplying the above equation by

Therefore, we obtain (22).

Theorem6LetA∈Cn,nand Ind(A)≤1 and the characteristic polynomial ofAD∈Cn,nbe as in (13).Then

fAD(A)=c1An+c2An-1+…+cn-1A2+A=0

(23)

LetA∈Cn,nand Ind(A)=k.Then the DMP inverse ofAisAd,+=ADAA+[3].Since (Ad,+)2=ADAA+ADAA+=ADAA+AADA+=(AD)2AA+, we obtain

(Ad,+)p=(AD)pAA+

(24)

wherepis a positive integer.

Theorem7Let the characteristic polynomial ofA∈Cn,nbe as in (1).Then

fA(Ad,+)=a1(Ad,+)n+a2(Ad,+)n-1+…+

an-1(Ad,+)2+Ad,+=0

(25)

ProofBy applying (1)and Theorem 2, we obtain

a1(AD)nAA++a2(AD)n-1AA++…+

an-1(AD)2AA++ADAA+=0

From (24), we can obtain (25).

[1]Ben-Israel A, Greville T N E.Generalizedinverses:Theoryandapplications[M].2nd ed.Berlin: Springer, 2003: 163-168.

[2]Manjunatha Prasad K, Mohana K S.Core-EP inverse[J].LinearandMultilinearAlgebra, 2014,62(6): 792-802.DOI:10.1080/03081087.2013.791690.

[3]Malik S B, Thome N.On a new generalized inverse for matrices of an arbitrary index[J].AppliedMathematicsandComputation, 2014,226: 575-580.DOI:10.1016/j.amc.2013.10.060.

[4]Gao Y, Chen J, Ke Y.*-DMP elements in *-semigroups and *-rings[J].arXivpreprint.arXiv: 1701.00621, 2017.

[5]Li T, Chen J.Characterizations of core and dual core inverses in rings with involution[J].LinearandMultilinearAlgebra, 2017: 1-14.DOI: 10.1080/03081087.2017.1320963.

[6]Wang H.Core-EP decomposition and its applications[J].LinearAlgebraandItsApplications, 2016,508: 289-300.DOI:10.1016/j.laa.2016.08.008.

[7]Zou H, Chen J, Patrìcio P.Characterizations ofm-EP elements in rings[J].LinearandMultilinearAlgebra, 2017: 1-13.DOI: 10.1080/03081087.2017.1347136.

[8]Prasad K M, Mohana K S.Core-EP inverse[J].LinearandMultilinearAlgebra, 2014,62(6): 792-802.DOI:10.1080/03081087.2013.791690.

[9]Kaczorek T.Cayley-Hamilton theorem for fractional linear systems[C]//8thConferenceonNon-IntegerOrderCalculusandItsApplications.Zakopane, Poland, 2017: 45-56.DOI:10.1007/978-3-319-45474-0_5.

[10]Kaczorek T.An extension of the Cayley-Hamilton theorem for nonlinear time-varying systems[J].InternationalJournalofAppliedMathematicsandComputerScience, 2006,16: 141-145.

[11]Kaczorek T.Cayley-Hamilton theorem for Drazin inverse matrix and standard inverse matrices[J].BulletinofthePolishAcademyofSciencesTechnicalSciences, 2016,64(4): 793-797.DOI:10.1515/bpasts-2016-0088.

[12]Feng L G, Tan H J, Zhao K M.A generalized Cayley-Hamilton theorem[J].LinearAlgebraandItsApplications, 2012,436(7): 2440-2445.DOI:10.1016/j.laa.2011.12.015.

[13]Hwang S G.A generalized Cayley-Hamilton theorem for polynomials with matrix coefficients[J].LinearAlgebraandItsApplications, 2011,434(2): 475-479.DOI:10.1016/j.laa.2010.08.039.

[14]Horn R A, Johnson C R.Matrixanalysis[M].Cambridge,UK: Cambridge University Press, 2012: 109-111.

[15]Wang H, Liu X.Partial orders based on core-nilpotent decomposition[J].LinearAlgebraanditsApplications, 2016,488: 235-248.DOI:10.1016/j.laa.2015.09.046.