基于六维线性插值的六自由度机械臂逆运动学方程求解方法
2018-04-12陈小平
周 锋,林 楠,陈小平
(中国科学技术大学 多智能体系统实验室,合肥 230026)(*通信作者电子邮箱zf062@mail.ustc.edu.cn)
0 引言
六自由度(Degrees Of Freedom, DOF)机械臂逆运动学求解问题一直是机器人领域研究的热点。对于特殊结构的六自由度机械臂,连续三个关节平行或三个关节轴线相交于一点,则必有封闭解,可以使用代数法如几何法[1]、指数积方法[2]求解运动学反问题。可对于一般几何结构的六自由度串联机械臂,以上方法求解计算复杂度很高或不可解,主要求解方法以数值解为主,如双四元数[3]、李代数[4]、迭代法(如Newton-Raphson迭代算法[5])等,但理论复杂,且迭代法还需求解雅克比矩阵,运算复杂、用时久,因而研究方向转向启发式算法。Kalra等[6]将遗传算法应用到六自由度机械臂逆运动学问题的求解中;Chiddarwar等[7]则将神经网络应用到六自由度机械臂逆运动学问题的求解中。神经网络是模拟函数关系,对于逆运动中一个位姿对应多个关节角的非函数映射,只能在局部模拟处理,当输入数据较少或较多时预测效果都会有所下降,不易控制。
一维插值主要有牛顿插值、拉格朗日插值、Hermite插值和三次样条插值。一维插值在机器人领域一般应用在关节空间轨迹规划,常用的有三次多项式、五次多项式[8]。二维插值主要有反距离加权插值法、克里金插值法、最小曲率法、改进谢别德法、自然邻近插值法、最近邻近插值法、多元回归法、径向基函数法、线性插值三角网法、移动平均法和局部多项式法。二维插值一般应用在降水量分析[9]、海洋环境数据处理[10]等应用中。在插值领域,分段线性插值能够稳定、有效地逼近目标函数,但对于本文要研究的六自由度机械臂逆运动学求解问题,当前的插值方法维度较低。
针对一般结构的六自由度机械臂逆运动学方程求解困难的问题,本文提出六维线性插值及反插值理论,利用当前关节角附近的7个相邻的关节角点发现运动规律,逼近目标位姿。与径向基网络(Radical Basis Function Network, RBFN)相比,反插值法预测的关节角对应的位姿可迅速逼近目标位姿;与Newton-Raphson迭代算法相比,反插值法不需要求解雅克比矩阵,只需知道机械臂的运动数据,利用差商代替微商求解逆运动学解,计算复杂度较低。
1 六自由度机械臂结构
由于D-H坐标系法的关节参数的下标与关节轴不对应,所以本文采用Khalil等提出的约定[11]建立参考坐标系,本文设计的六自由度机械臂的参考坐标系如图1所示,每个圆柱体代表一个电机,每个箭头所指方向是电机轴的朝向,0坐标系为基坐标系,7坐标系为末端执行器坐标系,在初始状态下,7坐标系与0坐标系各坐标轴朝向相同。各关节参数如表1所示。
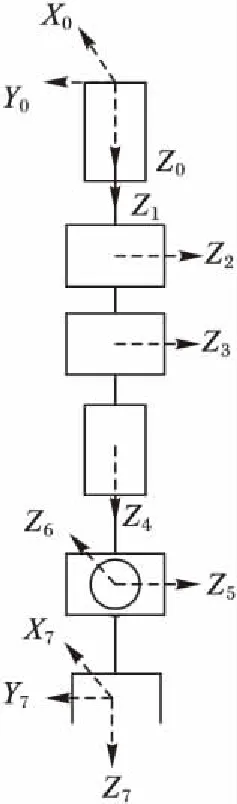
图1 六自由度机械臂坐标系Fig. 1 Coordinate system of 6-DOF manipulator

表1 各关节几何参数Tab. 1 Geometric parameters of every joint
在Khalil等提出的约定[11]下,通过绕xi-1轴旋转角度αi,沿xi-1轴平移αi,绕zi轴旋转角度θi,沿zi轴平移di,可实现参考坐标系i相对于参考坐标系i-1的定位。
绕xi-1轴旋转角度αi的变换矩阵为:
(1)
沿xi-1轴平移ai的变换矩阵为:
(2)
绕zi轴旋转角度θi的变换矩阵为:
(3)
沿zi轴平移di的变换矩阵为:
(4)
通过这些独立变换的串联:
Rot(xi-1,αi)Trans(xi-1,ai)Rot(zi,θi)Trans(zi,di)
(5)
得到参考坐标系i相对于参考坐标系i-1的等价齐次变换矩阵为:
i-1Ti=
(6)
(7)
2 末端执行器位姿描述
本文使用ZYX型欧拉角描述姿态,定义如图2所示,首先绕z轴将x轴旋转到x′轴在xoy平面内的投影x″,然后绕y(y″)轴旋转使x(x″)轴与x′轴重合,然后再绕x(x′)轴使y(y″)轴与y′轴重合。经以上三个步骤,便从xyz坐标系得到了x′y′z′坐标系,在变换过程中形成的三个角度分别为α、β、γ,为x′y′z′坐标系相对xyz坐标系的欧拉角参数。

图2 改进后的欧拉角定义Fig. 2 Definition of improved Euler angle
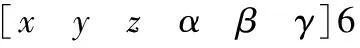
末端执行器坐标系相对基坐标系的位置参数为:
x=0T7(1,4)
(8)
y=0T7(2,4)
(9)
z=0T7(3,4)
(10)
其中:0T7是0坐标系(基坐标系)到7坐标系(末端执行器坐标系)的等价齐次变换矩阵;0T7(1,4)表示矩阵0T7的第一行第四列的那个元素。
末端执行器坐标系相对基坐标系的姿态参数为:
α=arctan2(0T7(2,1),0T7(1,1))
(11)
(12)
(13)
3 径向基网络
径向基网络(RBFN)是使用径向基函数的线性组合来模拟任一连续函数的,常用的径向基函数有高斯函数、反演S型函数和拟多二次函数。一个径向基函数(Radial Basis Function, RBF)神经网络的计算过程如下:
步骤1从训练数据中选取基函数的中心,常用的方法是K-means聚类。
步骤2在得到聚类中心后,径向基函数的扩展常数便可以通过计算各聚类中心之间的距离来得到。
步骤3计算输出权值即径向基函数的组合系数。
径向基网络在机械臂逆运动学中常用的方法是将位姿作为输入,关节角作为输出,网络结构如图3所示。

图3 RBFN结构Fig. 3 Structure of RBFN
RBF神经网络在正运动学方面的应用是比较有效的,因为机械臂的正运动学方程是函数关系,即一个自变量对应一个因变量;但在逆运动学方面,由于一个位姿对应多组关节角,不是函数关系,RBF神经网络的应用情况就会比较糟糕。可以通过筛选数据的方式,使在局部范围内呈现函数关系。具体算法流程如图4所示。
4 六维线性插值及反插值理论
径向基网络在局部模拟目标函数,当输入数据较少或较多时预测效果都会有所下降,不易控制,而分段线性插值可以稳定、有效地逼近目标函数。一维线性插值是在两个相邻节点(x1,y1)、(x2,y2)间建立一元一次函数y=a*x+b,可以对以这两个节点的区间内的值作预测,如给出x,求出对应的y,同时也能作反插值运算,即给出y求对应的x。二维线性插值的最小预测单元是由三个相邻的节点组成的三角面,其对应的插值函数为z=a*x+b*y+c。以此类推,六维线性插值的最小预测单元由7个相邻的非线性相关的节点组成,其对应的插值函数为:
x=a1*θ1+b1*θ2+c1*θ3+d1*θ4+e1*θ5+f1*θ6+g1
(14)
y=a2*θ1+b2*θ2+c2*θ3+d2*θ4+e2*θ5+f2*θ6+g2
(15)
z=a3*θ1+b3*θ2+c3*θ3+d3*θ4+e3*θ5+f3*θ6+g3
(16)
α=a4*θ1+b4*θ2+c4*θ3+d4*θ4+e4*θ5+f4*θ6+g4
(17)
β=a5*θ1+b5*θ2+c5*θ3+d5*θ4+e5*θ5+f5*θ6+g5
(18)
γ=a6*θ1+b6*θ2+c6*θ3+d6*θ4+e6*θ5+f6*θ6+g6
(19)
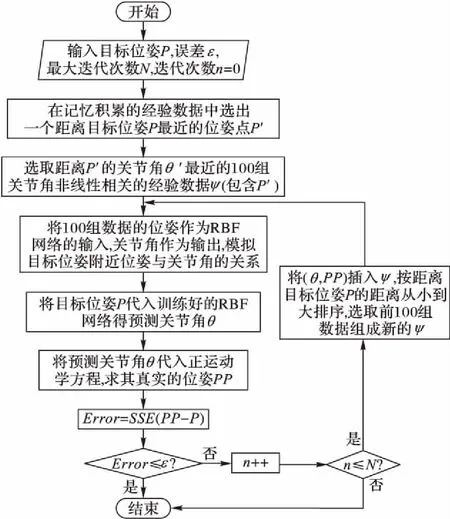
图4 RBF预测算法Fig. 4 RBF prediction algorithm
设第i个相邻节点的6个关节角度为:
其中θij代表第i个相邻节点的第j个关节的角度。
设第i个相邻节点的空间位姿为:
其中:xi、yi、zi为末端执行器坐标系的位置参数;αi、βi、γi为末端执行器坐标系的姿态参数。
则7个相邻的非线性相关的节点数据代入插值函数公式(14),有如下方程组:
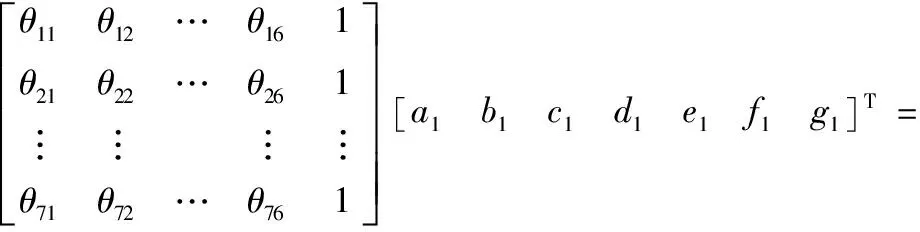
(20)
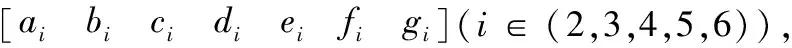
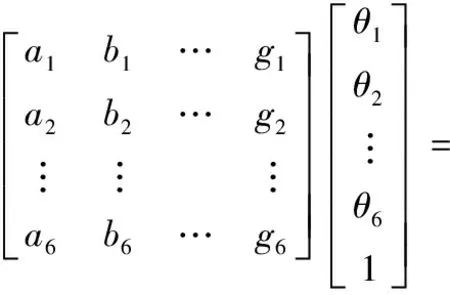
(21)

(22)
如果预测的关节角对应的位姿与目标位姿的距离大于给定精度,新预测的数据可以作为相邻的节点迭代预测,直至满足给定精度或超出最大迭代次数。
正向插值流程如图5所示。

图5 正向插值流程Fig. 5 Flow chart of forward interpolation
反向插值流程如图6所示。
其中,关节角的距离计算公式为:
dis=‖θ-θgoal‖
(23)
位姿的距离计算公式为:
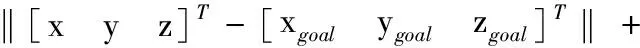
(24)
其中位置参数以mm为单位,姿态参数以度为单位。
5 仿真验证实验
实验硬件环境:一台计算机(CPU为Intel i5- 4460 3.2 GHz,内存为8 GB)。
实验软件环境:Matlab R2015b。
首先使用Matlab按照正运动学方程在限定每个关节活动角度为30°的范围内随机产生100万组经验数据,同时随机产生1万组测试数据。
从测试数据中随机选取30组待预测关节角,按照正向插值算法预测关节角对应的位姿,其中X坐标预测结果如图7所示。由图7可以看出,正向插值预测的位姿与实际位姿一致。
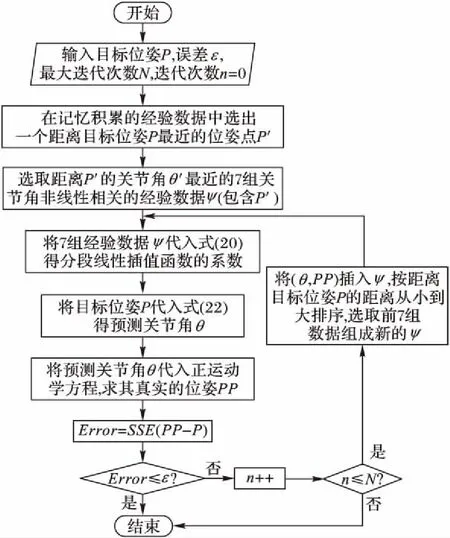
图6 反插值流程Fig. 6 Flow chart of inverse interpolation
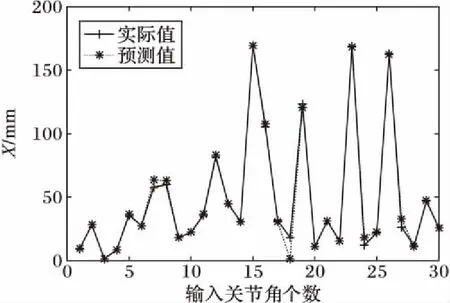
图7 正向插值结果Fig. 7 Forward interpolation results
从测试数据中随机选取一个目标位姿:

依据径向基网络(RBFN)求解逆运动学解算法,设定均方误差(Mean Squared Error, MSE)为0.1,最大神经元个数为1 000,误差为0,最大迭代次数为10,预测角度逼近目标位置的情况如表2所示。其中,角度和方差(Sum of Squares due to Error, SSE)为6个关节角参量和目标关节角参量的误差平方和,位姿SSE为6个位姿参量和目标位姿的误差平方和。由表2可以看出,随着迭代次数的增加,径向基网络预测的关节角对应的位姿慢慢逼近目标位姿,但是逼近速度缓慢。
按照反向插值步骤设置误差为0,最大迭代次数为10,实验结果如表3所示。由表3可以看出,在第三次反向插值时,位姿SSE(6个位姿参量和目标位姿的误差平方和)为0.002 2<1,说明位姿中三个位置参量的误差小于1 mm,三个姿态参量误差小于1°;第10次插值时,相邻的7个点相距很近,超出Matlab运算精度,矩阵奇异退出。六维线性反插值理论在收敛的情况下理论上可以求出给定位姿的任意精度的逆运动学解。

表2 RBF实验结果Tab. 2 Experimental results of RBF
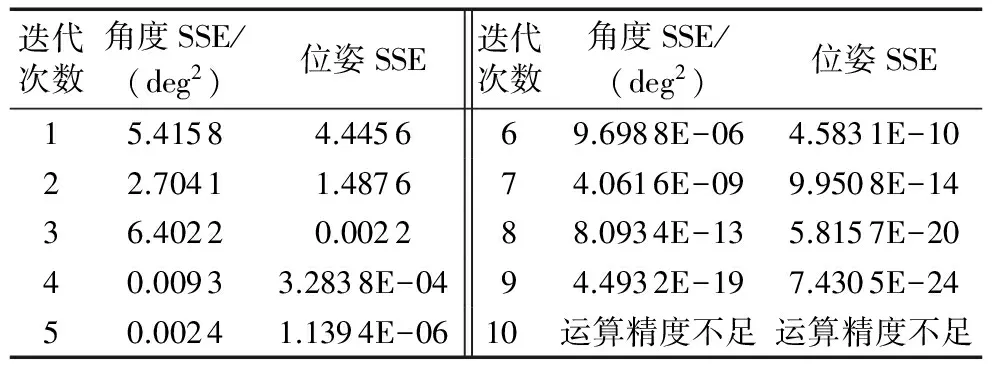
表3 反插值实验结果Tab. 3 Experimental results of reverse interpolation
随机选取30组位姿,设定误差为0,最大迭代次数为10,六维线性反插值和径向基网络预测的关节角对应的位姿的X坐标误差如图8所示。从图8中可以看出,径向基网络比较稳定,六维线性反插值法在一个点预测误差较大,但整体预测精度较高。径向基网络预测耗时2 034 s,插值法耗时127 s,插值法能够更快地作出预测。
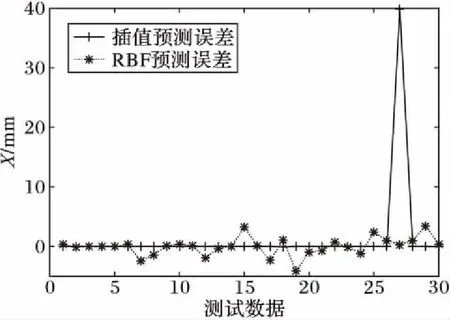
图8 反插值与RBF预测误差对比Fig. 8 Comparison of prediction error between inverse interpolation and RBF
随机选取10 000组测试数据,设定要求精度:位姿SSE<1,实验结果显示8 940组测试数据得到满足要求精度的逆运动学解,逆运动学求解率89.4%,求解率较高,能够满足机器人日常抓取的需求。
6 结语
针对一般结构的六自由度机械臂逆运动学方程求解困难的问题,本文借鉴径向基网络基于数据的求解思想,结合一维、二维线性插值理论,提出六维线性插值及反插值理论。实验结果表明本文提出的反插值法能够通过较少的迭代次数求出给定精度的逆运动学解,且逆运动学解的求解率较高。本文的方法虽然能够求解任意精度的逆运动学解,但求解率只达到了89.4%,未达到100%,下一步将研究提高求解率的方法;以及如何优化存储结构,在大批量的经验数据中快速找出7个相邻的非线性相关的节点。
参考文献(References)
[1]王英石.冗余机器人的运动学及轨迹规划研究[D].天津:南开大学,2014:15-32. (WANG Y S. Research on the kinematics and trajectory planning of redundant robots [D]. Tianjin: Nankai University, 2014: 15-32.)
[2]刘亚军,黄田.6R操作臂逆运动学分析与轨迹规划[J].机械工程学报,2012,48(3):9-15. (LIU Y J, HUANG T. Inverse kinematics and trajectory planning of 6R serial manipulators [J]. Journal of Mechanical Engineering, 2012, 48(3): 9-15.)
[3]QIAO S, LIAO Q, WEI S, et al. Inverse kinematic analysis of the general 6R robot made of RGRR-I [J]. Chinese Journal of Mechanical Engineering, 2010, 46(1): 30-36.
[4]ROCCO S D, EKLUND D, SOMMESE A J, et al. Algebraic C*-actions and the inverse kinematics of a general 6R manipulator [J]. Applied Mathematics and Computation, 2010, 216(9): 2512-2524.
[5]沈珑斌.冗余灵巧臂的示教学习[D].杭州:浙江大学,2014:16-17. (SHEN L B. Learning from demonstration for redundant manipulator [D]. Hangzhou: Zhejiang University, 2014: 16-17.)
[6]KALRA P, MAHAPATRA P B, AGGARWAL D K. An evolutionary approach for solving the multimodal inverse kinematics problem of industrial robots [J]. Mechanism and Machine Theory, 2006, 41(10): 1213-1229.
[7]CHIDDARWAR S S, BABU N R. Comparison of RBF and MLP neural networks to solve inverse kinematic problem for 6R serial robot by a fusion approach [J]. Engineering Applications of Artificial Intelligence, 2010, 23(7): 1083-1092.
[8]凌家良,施荣华,王国才.工业机器人关节空间的插值轨迹规划[J].惠州学院学报,2009,29(3):52-57. (LING J L, SHI R H, WANG G C. The industrial robot trajectory planning in joint space [J]. Journal of Huizhou University, 2009, 29(3): 52-57.)
[9]李艳,朱军,胡亚,等.不同插值方法模拟四川省逐月降水量的对比分析[J].水土保持研究,2017,24(1):151-160. (LI Y, ZHU J, HU Y, et al. Comparison analysis on different spatial interpolation methods to simulate monthly precipitation in Sichuan province [J]. Research of Soil and Water Conservation, 2017, 24(1): 151-160.)
[10]李峋,仵彦卿,范海梅.高维空间插值在海洋环境数据预处理中的应用[J].海洋环境科学,2009,28(6):729-733. (LI X, WU Y Q, FAN H M. Application of high-dimension interpolation method in pretreatment of marine environmental data [J]. Marine Environmental Science, 2009, 28(6): 729-733.)
[11]SICILIANO B, KHATIB O. Handbook of Robotics [M]. Berlin: Springer, 2007: 24-26.
[12]张欣.智能乒乓球发球机器人[D].厦门:厦门大学,2014. (ZHANG X. The intelligent table tennis serve robot [D]. Xiamen: Xiamen University, 2014.)
