基于双服务器模型的可公开验证多元多项式外包计算方案
2018-04-12罗小双杨晓元王绪安
罗小双,杨晓元,李 聪,王绪安
(1.武警工程大学 密码工程学院,西安 710086; 2.网络与信息安全武警部队重点实验室,西安 710086)(*通信作者电子邮箱yxyangyxyang@163.com)
0 引言
云计算技术成为互联网时代必不可少的工具,逐渐渗透到日常生活的方方面面。由于云具有强大的计算能力和存储能力[1],计算能力较弱的用户倾向于将复杂计算外包给云服务器来完成[2],从而降低本地计算的复杂度、减少计算量,提高用户的运算效率。但是数据一旦外包给云来完成,不可避免地会带来隐私泄露的安全问题。为了防止不可信云服务器泄露和滥用用户的数据,用户需要对交付给云服务器运算的数据进行加密或者盲化处理,以此来保证数据的隐私性和完整性;并且,用户能够对云服务器返回的计算结果进行验证,从而获得正确的计算结果。
2010年欧洲密码会议(CRYPTO 2010)上,Gennaro等[3]将外包计算[4]和验证技术结合起来,首次提出可验证计算(Verifiable Computation)的概念,运用混淆电路和全同态加密构造了一个可验证计算的外包方案,该方案能够保证输入与输出的隐私性,但是只能做到私有验证。2011年,Benabbas等[5]提出了选择明文攻击(Chosen Plaintext Attack, CPA)安全的多项式外包计算方案,解决了Gennaro等[3]留下的公开问题,该方案运用加法同态加密算法来保证多项式的隐私性,但是不能保证输入的隐私性和实现公开验证。Barbosa等[6]提出了可委托的同态加密(Delegatable Homomorphic Encryption, DHE)密码学原语,并给出了如何运用DHE构造可验证计算方案的方法。2012年,Fiore等[7]提出了可公开验证的多项式外包计算方案,但是不能保证输入和函数的隐私性。2013年,Zhang等[8]利用多线性映射和同态加密算法构造了单变量多项式外包计算方案,该方案能够保证输入的隐私性,其扩展方案保证了函数的隐私性,但是都只能做到私有验证。任艳丽等[9]在此基础上构造了多元多项式的可验证外包计算方案,同样只能做到私有验证。Papamanthou等[10]提出了动态多项式的可验证外包计算方案,允许对系数进行递增的更新。CCS2014,Fiore等[11]提出了适应性安全的可验证多项式外包计算方案,但是该方案只能保证函数的隐私性。为了减少存储开销,2015年,Zhang等[12]首次提出了批验证(Batch Verifiable Computation, BVC)的概念,构造了两个批验证的多项式外包计算方案,提出了如何构造可公开进行批验证的外包计算方案这一公开问题。2016年,Sun等[13]解决了这一公开问题,能够做到任何第三方都能有效验证服务器返回结果的正确性。
当前,可验证的安全外包计算方案大都基于单服务器模型,用户将外包数据交给单个云服务器来进行计算,并通过云服务器返回的辅助信息来验证结果的正确性,但是不能完全做到可公开验证的情况下保证输入和输出的隐私性,并且受限于预计算量较大、交互轮数较多等实际缺陷。实际情况下,云服务提供商并不仅限于单个实体,可能存在多个服务提供商同时提供服务。云服务提供商之间存在一定的竞争关系,因而不会为了短期利益而勾结在一起攻击用户隐私数据。本文利用多线性映射[14]和BGN(Boneh-Goh-Nissim)同态加密算法[15],提出了双服务器安全模型下的多元多项式外包计算方案,该方案能够同时保证输入和输出的隐私性,并且实现了可公开验证的功能。分析结果表明,本文方案在安全性上能够达到CPA安全,用户的计算代价远远小于服务器以及直接计算多元多项式函数的计算代价。
1 预备知识
1.1 BGN加密算法
BGN加密算法[15]支持任意次的加法同态操作和一次乘法同态操作。其具体算法如下所示:
1)密钥生成(KeyGen(1λ)→pk,sk):选择安全参数λ∈Z+,生成元组(p,q,G,G1,e)。其中:p和q分别是两个不同的大素数,循环群G的阶为N=pq,双线性映射e:G×G→G1,G1的阶为g1=e(g,g)。从G中随机选择两个生成元g和u,令h=uq,h1=e(g,h)。公钥pk={N,G,G1,e,g,h},私钥sk=p。
2)加密(Enc(m,pk)→c):从{1,2,…,N}中随机选择一个r,用公钥pk加密消息m∈M,输出密文c,即c=gmhr∈G1。
3)解密(Dec(c,sk)→m):用私钥sk解密密文c输出m∈M,即cp=(gp)m。
BGN加密算法其同态性质为:给定两个密文c1=gm1hr1和c2=gm2hr2,则:
1)加法同态:c1·c2=gm1hr1·gm2hr2=gm1+m2·hr1+r2,即Enc(m1+m2)=c1·c2。
2)乘法同态:存在某个δ∈ZN,使得h=gqδ。则:
e(c1,c2)=e(gm1hr1,gm2hr2)=e(gm1+qδr1,gm2+qδr2)=
所以Enc(m1·m2)=e(c1,c2)。
1.2 多线性映射
1.3 安全模型
可验证计算中,用户将编码后的函数f和输入x发送给云服务器,云服务器能够计算出被编码的f(x)和一个附加证明,用户验证云服务器的计算结果是否正确并输出。方案Π=(KeyGen,ProbGen,Compute,Verify)由四部分组成,其具体描述如下:
1)(pk,sk)←KeyGen(1λ,f):输入安全参数λ和函数f,产生公钥pk和私钥sk。
2)(σ,τ)←ProbGen(sk,x):输入私钥sk和x,产生编码后输入σ和可验证密钥τ。
3)(ρ,π)←Compute(pk,σ):输入公钥pk和编码后输入σ,产生编码后的输出ρ和证明π。
4){f(x),⊥}←Verify(sk,τ,ρ,π):输入私钥sk和可验证密钥τ,编码后的输入ρ和证明π,输出f(x)或者⊥。
下面介绍可验证计算的安全模型,包括可验证性和隐私性[9]。
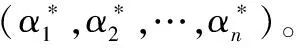
Setup阶段:B执行Setup算法,并将公钥pk发送给A。
Phase1阶段:A对B进行输入的加密询问:A将(α1,α2,…,αn)发送给B,B将σ=(σα1,σα2,…,σαn)返回给A。该询问可重复多次。
如果多项式时间内敌手经过q次询问后都不能以大于ε的概率赢得上述游戏,则可公开验证多元多项式外包计算方案是可验证的。
输入隐私性可以通过三个参与者进行下列游戏,包括敌手A,模拟器S和挑战者B。
Setup阶段:S与B执行Setup算法,并把公钥pk发送给A。
Phase1阶段: A发送函数输入(α1,α2,…,αn)给S进行加密询问,S返回σ=(σα1,σα2,…,σαn)给A。该询问可重复多次。
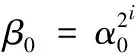
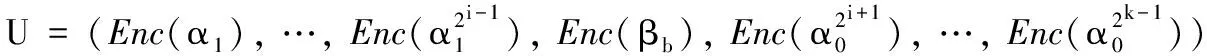

1.4 困难问题
本文方案的隐私性和安全性依赖于子群判定假设(Subgroup Decision Assumption, SDA)问题[8]。
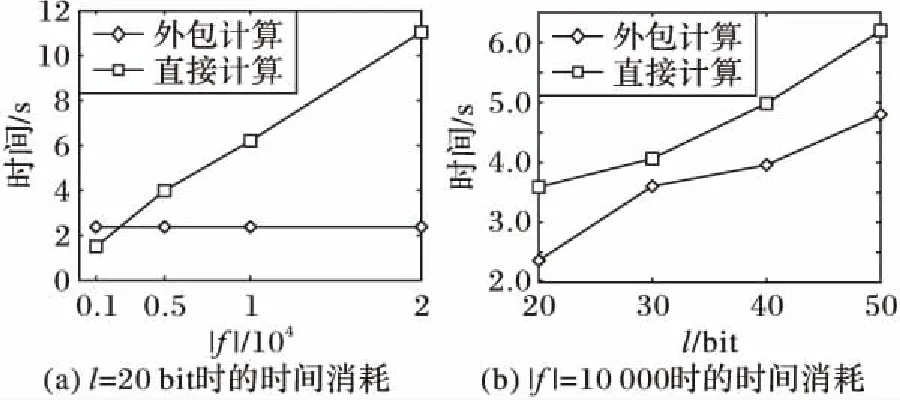
定义2SDA问题。如果对于任意概率多项式敌手A,|Pr[A(Γk,u)=1]-Pr[A(Γk,uq)=1]| 1)BGNk加法同态操作:Enc(m1+m2+…+mk)=Enc(m1)·Enc(m2)·…·Enc(mk)。 2)BGNk乘法同态操作:Enc(m1·m2·…·mk)=ek(Enc(m1),Enc(m2),…,Enc(mk))。 现基于上述的计算方法介绍本文方案算法如下: σf(α1,α2,…,αn)=Enc(f(α1,α2,…,αn))= 所以ρ1=e(Enc(f(α1,α2,…,αn)),Enc(γ))=e(σf(α1,α2,…,αn),ψγ)。同理,云服务器S2接收到用户发送来的σ后,计算得到 和 4)验证结果Verify(ρ1,ρ2):用户接收到ρ1和ρ2,验证e(ψγ,ρ2)=e(ψη,ρ1)是否成立。如果等式成立,则用户输出f(α)。 引理1如果两个不可勾结的云服务器是诚实的,则y=f(α1,α2,…,αn)成立。 证明因为 e(ψγ,ρ2)=e(Enc(γ),Enc(ηf(α1,α2,…,αn)))= Enc(γηf(α1,α2,…,αn)) e(ψη,ρ1)=e(Enc(η),Enc(γf(α1,α2,…,αn)))= Enc(ηγf(α1,α2,…,αn)) 如果云服务器返回的值是正确的,则e(ψγ,ρ2)=e(ψη,ρ1)成立。 因为: 所以: 因此,用户解密e(ψγ,ρ2)p便能够计算出y=f(α1,α2,…,αn)。 上述方案Π输入的隐私性基于SDA问题,两个不可勾结的不可信云服务器不能区分用户的两个不同输入,从而保证输入数据的安全性;并且方案Π能够验证结果的正确性,使得云服务器不会迫使用户接收伪造的返回值y≠f(α1,α2,…,αn)。 引理2如果SDA对于Γkn+2来说是困难问题,则本文方案Π能够获得输入输出隐私安全。 1)模拟者S选择多元多项式 然后将公钥(N,G1,G2,…,Gkn+2,e,g1,g2,…,gkn+2,h)发送给A。 因此: Pr[B|i=l,b=1]Pr[b=1])= Pr[b′=1|i=l,b=1])= Pr[A(pk,Ul+1)=1])= 即敌手A能够至少以不可忽略的概率ε/k来攻破BGNkn+2语义安全。当SDA问题成立时,该假设不成立。 同理,用户将参数ψγ和ψη公开,敌手A也不能攻破BGNkn+2语义安全来区分两个不同的输入γ0和γ1以及输入η0和η1。当SDA困难问题成立时,敌手也不能攻破BGNkn+2语义安全来区分两个不同的输出。 综上所述,本文方案Π能够获得输入输出的隐私安全。 引理3假设两个不可勾结的云服务器从用户接收的输入隐私安全,并且BGNkn+2加密方案安全,则本文方案Π能够验证结果的正确性,获得正确的输出。 证明假设存在恶意敌手A以不可忽略的概率ε攻破BGNkn+2加密方案,当用户公开参数ψγ和ψη后,恶意敌手A(包括云服务器S1)能够破解找到γ′使得γ′=γ的概率为Pr[γ′=γ]≥ε,同时得到η′和f′(α1,α2,…,αn)的概率分别都为Pr[η′=η]≥ε和Pr[f′(α1,α2,…,αn)=f(α1,α2,…,αn)]≥ε,故而敌手A伪造出γ′η′f′(α1,α2,…,αn)的概率为Pr[γ′η′f′(α1,α2,…,αn)=γηf(α1,α2,…,αn)]≥ε3。 同理,恶意敌手A′(包括云服务器S2)能够伪造出γ″使得γ″=γ的概率为Pr[γ″=γ]≥ε,同时得到η″和f″(α1,α2,…,αn)的概率分别都为Pr[η″=η]≥ε和Pr[f″(α1,α2,…,αn)=f(α1,α2,…,αn)]≥ε,故而敌手A伪造出γ″η″f″(α1,α2,…,αn)的概率为Pr[γ″η″f″(α1,α2,…,αn)=γηf(α1,α2,…,αn)]≥ε3。因为两个云服务器S1和S2不能相互勾结串通,所以恶意敌手伪造出γ″η″f″(α1,α2,…,αn)=γ′η′f′(α1,α2,…,αn)使得通过公开验证e(ψγ,ρ2)=e(ψη,ρ1)的概率为Pr[e(ψγ,ρ2)=e(ψη,ρ1)]≥(ε3)·(ε3)=ε6,即敌手至少能够以ε6的概率通过用户或公共的验证。当SDA问题成立时,BGNkn+2加密方案安全,该假设不成立。 定理1如果SDA成立,则基于两个不可勾结的云服务器的外包计算方案是满足输入隐私安全的可公开验证方案。 证明结合引理1~3可证明该定理。为了保证多元多项式函数的隐私性,用户可以对多项式系数进行加密得到Enc(fi1,i2,…,in),然后传送给两个不同的云服务器S1和S2。云服务器计算出 从而计算出Enc(f(α1,α2,…,αn)),并且可以证明该方案输入与多项式函数的隐私性和安全性。 表1 本文方案效率分析Tab. 1 Efficiency analysis of the proposed scheme 为了更加清晰地展示本文方案的高效性,对其进行了性能测试,运行环境为64位Windows操作系统,频率为2.5 GHz 4核Core i5 CPU,内存4 GB,采用密码函数库jPBC(java Pairing-Based Cryptography)TypeA1合数阶对称双线性群进行仿真实验。分别测试了BGN加解密算法、双线性对运算的平均运行时间,具体如表2所示。对n元d阶多项式进行测试时,实验参数设置为安全参数|λ|=20 bit,n=4,k=6,d=63,多项式输入αi的长度l分别为20、30、40、50 bit,多项式项数|f|分别设置为1 000、5 000、10 000、20 000,其平均运行时间如表3所示。 表2 基本密码学操作时间开销 msTab. 2 Time overhead of fundamental cryptographic operations ms 本文分别大致计算出不同输入长度(l)时用户计算的时间消耗,然后与直接计算多项式的时间消耗进行对比分析。当l固定长度为20 bit时,其运行时间如图1(a)所示;随着多项式项数的逐渐增多,本文方案外包计算的优势逐渐显示出来,其时间消耗只与多项式的深度有关,不会随着多项式项数的增加而增加;当多项式项数固定为10 000时,其运行时间如图1(b)所示,本文方案外包计算的时间消耗小于直接计算的时间消耗,但会随着输入长度的增加而增加。 表3 4元63阶多项式平均运行时间 msTab. 3 Average running time of 4-variate 63-order polynomials ms 图1 外包计算和直接计算时间对比Fig. 1 Computing time comparison between outsourced and direct computation 通过理论分析与实践对比,外包计算方案中用户的计算量远远小于直接计算函数的计算量,也小于云服务器的计算量,因此该方案是高效的可验证外包计算方案。 利用多线性映射和BGN同态加密算法,设计了可公开验证的多元多项式外包计算方案。该方案基于双服务器模型,用户需要向两个云服务器发送外包数据,利用两个不可勾结的云服务器的计算能力,计算出两个不同的结果,用户或者第三方可以通过公开的数据对结果进行验证,如果验证通过,用户可以用私钥解密得到多项式的值。方案的输入采用同态加密算法进行处理,在标准模型下达到CPA安全,能够保证输入与输出的隐私性,并且能够做到公开验证。但是为了保证输入输出的隐私性与安全性,方案均采用同态加密算法进行加密,一定程度上增加了计算、通信和存储复杂度。如何利用非同态加密技术对数据进行处理,同时针对多个多元多项式函数进行外包计算或者实现批验证是提高多项式外包计算效率的研究重点。 参考文献: [1]ABO-ALIAN A, BADR N L, TOLBA M F. Data storage security service in cloud computing: challenges and solutions [M]// Multimedia Forensics and Security, Intelligent Systems Reference Library, vol 115. Cham: Springer, 2017: 25-57. [2]曹珍富.密码学的新发展[J].四川大学学报(工程科学版),2015,47(1):1-12. (CAO Z F. New development of cryptography[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(1): 1-12.) [3]GENNARO R, GENTRY C, PARNO B. Non-interactive verifiable computing: outsourcing computation to untrusted workers [C]// CRYPTO 2010: Proceedings of the 2010 Conference on Advances in Cryptology, LNCS 6223. Berlin: Springer, 2010: 465-482. [4]李勇,曾振宇,张晓菲.支持属性撤销的外包解密方案[J].清华大学学报(自然科学版),2013,53(12):1664-1669. (LI Y, ZENG Z Y, ZHANG X F. Outsourced decryption scheme supporting attribute revocation [J]. Journal of Tsinghua University (Science and Technology), 2013, 53(12): 1664-1669.) [5]BENABBAS S, GENNARO R, VAHLIS Y. Verifiable delegation of computation over large datasets [C]// CRYPTO 2011: Proceedings of the 2011 Annual Cryptology Conference, LNCS 6841. Berlin: Springer, 2011: 111-131. [6]BARBOSA M, FARSHIM P. Delegatable homomorphic encryption with applications to secure outsourcing of computation [C]// CT-RSA 2012: Proceedings of the Cryptographers’ Track at the RSA Conference, LNCS 7178. Berlin: Springer, 2011: 296-312. [7]FIORE D, GENNARO R. Publicly verifiable delegation of large polynomials and matrix computations, with applications [C]// CCS ’12: Proceedings of the 2012 ACM Conference on Computer and Communications Security. New York: ACM, 2012: 501-512. [8]ZHANG L F, SAFAVI-NAINI R. Private outsourcing of polynomial evaluation and matrix multiplication using multilinear maps [C]// Proceedings of the 12th International Conference on Cryptology and Network Security, LNCS 8257. Cham: Springer, 2013: 329-348. [9]任艳丽,谷大武,蔡建兴,等.隐私保护的可验证多元多项式外包计算方案[J].通信学报,2015,36(8):23-30. (REN Y L, GU D W, CAN J X, et al. Verifiably private outsourcing scheme for multivariate polynomial evaluation [J]. Journal on Communications, 2015, 36(8): 23-30.) [10]PAPAMANTHOU C, SHI E, TAMASSIA R. Signatures of correct computation [C]// Proceedings of the 10th Theory of Cryptography Conference on Theory of Cryptography, LNCS 7785. Berlin: Springer, 2013: 222-242. [11]FIORE D, GENNARO R, PASTRO V. Efficiently verifiable computation on encrypted data [C]// CCS ’14: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security. New York: ACM, 2014: 844-855. [12]ZHANG L F, SAFAVI-NAINI R. Batch verifiable computation of polynomials on outsourced data [C]// ESORICS 2015: Proceedings of the 2015 European Symposium on Research in Computer Security, LNCS 9327. Cham: Springer, 2015: 167-185. [13]SUN Y, YU Y, LI X, et al. Batch verifiable computation with public verifiability for outsourcing polynomials and matrix computations [C]// Proceedings of the 21st Australasian Conference on Information Security and Privacy: Part I, LNCS 9722. Cham: Springer, 2016: 293-309. [14]GARG S, GENTRY C, HALEVI S. Candidate multilinear maps from ideal lattices [C]// EUROCRYPT 2013: Proceedings of the 2013 Annual International Conference on the Theory and Applications of Cryptographic Techniques, LNCS 7881. Berlin: Springer, 2012: 1-17. [15]BONEH D, GOH E-J, NISSIM K. Evaluating 2-DNF formulas on ciphertexts [C]// TCC 2005: Proceedings of the 2005 Theory of Cryptography Conference, LNCS 3378. Berlin: Springer, 2005: 325-341.2 可公开验证多项式外包计算方案
2.1 基于多线性映射的扩展BGN同态加密算法
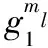
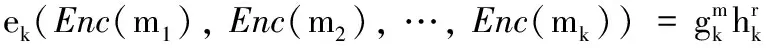
2.2 基于扩展BGN同态加密的基础计算方法
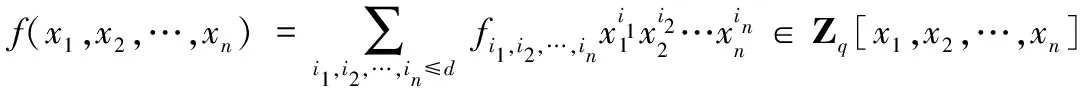
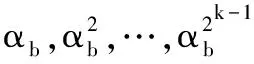
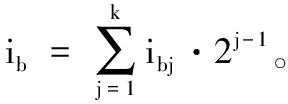
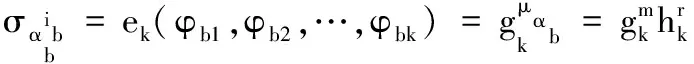
2.3 基于双服务器模型的可公开验证外包计算方案
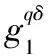
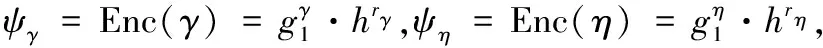
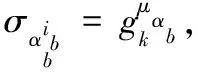
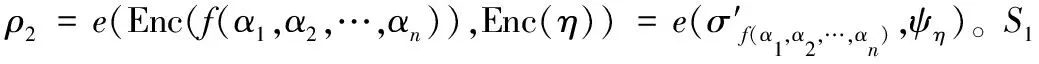
3 方案分析
3.1 正确性分析

3.2 安全性分析
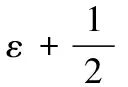
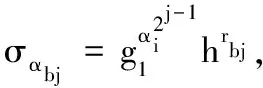
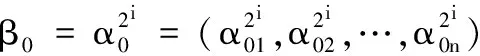

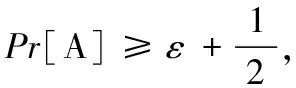
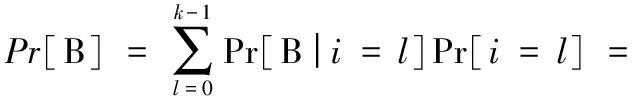
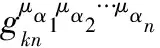
3.3 性能分析

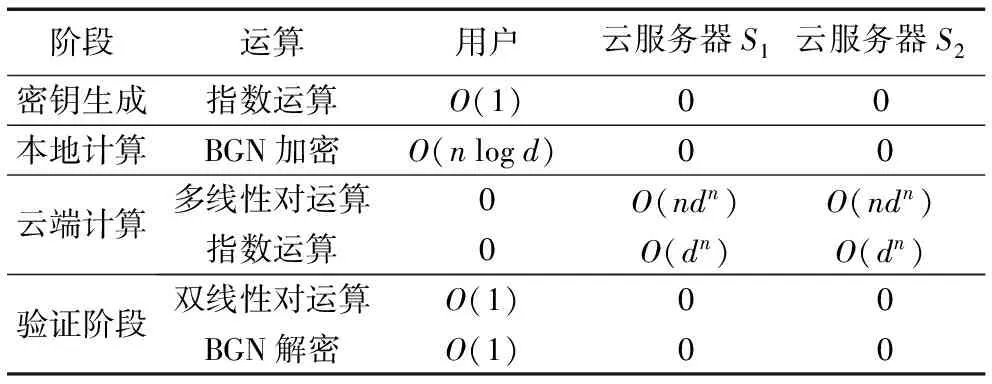

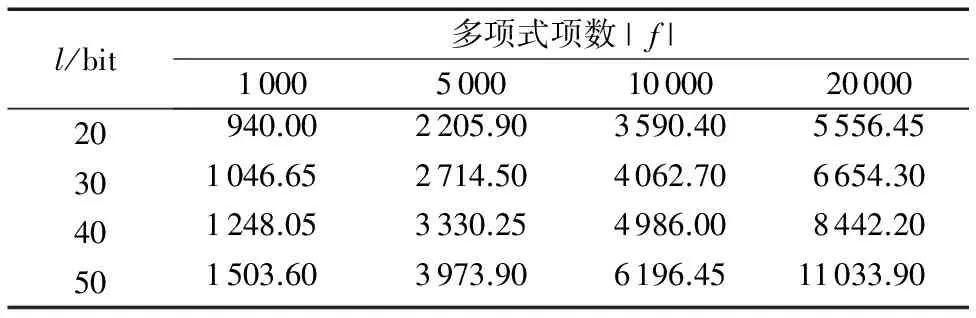
4 结语
