一种基于逆向导航的双轴旋转惯导系统自标定方法
2018-04-12任宏文曹亚林李文耀
林 山,任宏文,曹亚林,李文耀,刘 辉
(北京自动化控制设备研究所,北京100074)
0 引言
误差标定技术是惯导系统的关键技术之一,通过事先对系统误差参数进行估计标定,在实际导航过程中对误差进行补偿,从而消除系统误差参数对导航精度的影响[1]。采用系统级标定方法,通过观测系统导航误差,根据误差方程反推出引起导航误差的参数误差,能够降低对标定设备的要求,提升标定效率。双轴旋转惯导系统自身的旋转机构的精度满足系统级标定的要求,因此可利用其实现自标定,从而免去了惯导系统从载体上拆卸、利用转台标定后再次安装的环节,很大程度上降低了标定的工作时间和成本,提高了惯导系统的可靠性和可维护性[2]。因此自标定技术成为双轴旋转惯导系统标定技术研究的热点之一。
提高惯导系统标定精度和缩短标定时间是标定技术主要的研究方向,但两者是相互矛盾的。对标定数据的重复利用是提高标定精度和缩短标定时间的重要途径。2007年,严恭敏等提出了一种基于逆向导航算法的捷联惯导系统动基座对准方法,利用逆向导航算法实现了对准数据的重复利用,缩短了对准时间[3]。2014年,李京书等针对文献[3]逆向导航算法中进行小角度近似,在对同一组数据多次处理时会引起误差放大的问题,严格推导了逆向导航算法,避免了多次迭代造成的误差放大[4]。本文参考逆向导航算法在对准中的应用,结合双轴旋转惯导系统自标定的特点,提出了一种基于逆向导航的双轴旋转惯导系统自标定方法,在不增加标定转位和数据采集时间的情况下,对一组标定数据进行连续充分挖掘,提高数据的利用率,从而实现双轴旋转惯导系统的高精度自标定。
1 双轴旋转惯导系统标定基本原理
定义坐标系如下:记地心惯性坐标系为i系;记地球坐标系为e系;选取北天东地理坐标系为导航坐标系,记为n系;选取前上右坐标系为惯导坐标系(或载体坐标系),记为b系。
1.1 系统误差方程
根据惯性导航算法基本原理,直接给出在导航坐标系下双轴旋转惯导系统速度和失准角误差方程分别如下[5]:
(1)
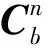
根据文献[6],建立陀螺和加表误差模型:
(2)
(3)
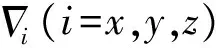
1.2 Kalman滤波器设计
以姿态角误差、速度误差、陀螺和加速度计零偏、陀螺和加速度计标度因数误差、安装误差为状态变量,以速度误差为观测量建立状态方程如下:
Z=HX+υ
(4)
式中,系统状态量为
Z=[δVnδVuδVe]T
(6)
状态量中的陀螺漂移、加表零偏、加表二次项误差、陀螺和加表的标度因数误差和安装误差均可看作随机常值误差项进行处理,微分均为零[7-8]。其余状态量对应的系统矩阵表达式由误差方程给出。
采用标准Kalman滤波方程:
Pk=(I-KkHk)Pk/k-1
(7)
利用上述Kalman滤波器,通过设计合理的转动方案对24个误差参数进行激励,可以实现惯导系统的标定。
2 基于逆向导航的标定方法
为了提高标定精度,需要对标定数据进行深入挖掘,本文提出的基于逆向导航的自标定方法,可以实现数据正向和逆向处理之间的转换,对标定数据进行不间断的正、逆向处理,同时进行系统误差参数辨识,即实现了不间断迭代运算;并且可以利用粗对准阶段的数据进行误差辨识,进一步提高了数据的利用率。本节根据正向导航算法,结合逆向导航过程的特点,推导了逆向导航算法,给出了基于逆向导航的自标定方法。
2.1 正向导航算法
双轴旋转惯导系统的姿态、速度和位置导航算法可用如下一组微分方程表示[3]:
(8)
(9)
计算机实际解算时,需要将式(8)离散化为[9]:
(10)
(11)
(12)
其中,Tn表示导航解算周期,P表示位置。
2.2 逆向导航算法推导
逆向导航算法是对导航数据按时间逆序求解,过程恰好与正向导航解算相反[10]。
首先对姿态更新算法取反
(13)
(14)
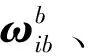
然后,对速度和位置更新算法取反
(15)
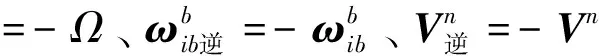
(16)
最后,可得位置更新方程
(17)
2.3 基于逆向导航的自标定方法
根据惯导系统误差模型,选取式(5)中提到的24个误差参数作为标定参数,为保证所有误差参数均具有可观测性,标定路径采用19位置标定路径[11]。具体标定流程如下。
首先,控制旋转机构按照19位置标定路径依次转动,每个位置停留一定时间,利用1.2节设计的Kalman滤波器对系统参数误差进行辨识,同时将标定起始时刻ts到结束时刻te的陀螺和加速度计采样数据存储下来[3];当正向导航、滤波完成后,以te时刻速度、位置、姿态信息为初始条件,利用逆向导航算法,实现从te到ts时刻的逆向导航,同时继续进行Kalman滤波运算;如此往复,直到标定参数变化满足迭代截止条件,从而提高标定精度。
3 仿真验证
为了验证标定方法的可行性,设计、搭建了数学仿真平台。采用数据发生器模拟生成标定转位运动轨迹数据,输出陀螺和加速度计的采样值作为标定仿真程序的输入,进行正、逆向导航解算和Kalman滤波,辨识24个误差参数。
3.1 数据发生器设置
数据发生器参数设置如下。
1)常值参数设置如表1所示。

表1 常值参数
2)误差参数设置如表2所示。
3.2 标定仿真结果分析
利用数据发生器生成的陀螺和加速度计采样值进行仿真,得到误差参数估计残差如表3所示,其中迭代次数定义为:第1次正向导航滤波作为第0次迭代,其后每进行一次正向导航滤波或逆向导航滤波,迭代次数加1。

表2 误差参数设定值

表3 误差参数估计残差
由表3可见,随着迭代次数的增加,各误差参数的估计残差均有不同程度的减小。
选取陀螺漂移和标度因数画出滤波估计曲线如图1、图2所示,可以直观地看出随着正、逆向导航滤波次数增加,陀螺漂移估计值逐渐接近设定值。
4 导航试验验证
为进一步验证标定方法的可行性,利用某型双轴旋转惯导系统,采用标定补偿前、后的系统参数进行1.5h静态导航试验,纯惯性定位精度如图3所示,对比可见,标定补偿后定位精度提高31%,表明本文所述标定方法能有效提高标定精度。
5 结论
本文提出了一种基于逆向导航算法的双轴旋转惯导系统自标定方法,给出了惯导系统误差方程,详细推导了逆向导航算法,设计了基于逆向导航算法的自标定方法,并搭建了数学仿真平台。对标定方法进行仿真验证,结果表明与单次导航滤波相比,经过几次正、逆向导航滤波后标定精度明显提高。
利用某型双轴旋转惯导系统,对所提标定方法进行了试验验证,结果表明采用本文标定方法得到的参数标定结果进行导航解算,定位精度有明显提高。利用本标定方法可以实现双轴旋转惯导系统的高精度自标定,提高惯导系统的可维护性、延长返厂维护周期,从而提高导航精度、延长载体的值班时间,因此该标定方法具有较高的工程应用价值。
[1]唐汇河, 胡平华, 黄鹤,等. 基于低精度离心机的平台惯导系统加速度计高精度系统级标定方法[J]. 导航定位与授时, 2016, 3(5):5-10.
[2]黄湘远, 汤霞清, 武萌,等. 外场条件下战车捷联惯导系统原位快速多位置标定技术[J]. 火炮发射与控制学报, 2014,35(1):65-70.
[3]严恭敏,严卫生,徐德民.逆向导航算法及其在捷联罗经初始对准中的应用[C]// 第27届中国控制会议.昆明, 2008:72.
[4]李京书, 许江宁, 何泓洋,等. 严格逆向过程的罗经回溯对准方法[J]. 系统工程与电子技术, 2014, 36(2):348-353.
[5]秦永元.惯性导航(第二版)[M]. 北京:科学出版社, 2005: 355-361.
[6]雷宏杰, 王晓斌, 刘放. 机载双轴旋转调制激光惯性导航系统误差特性及关键技术分析[J]. 导航定位与授时, 2016, 3(4):13-18.
[7]Chung D, Lee J G, Chan G P, et al. Strapdown INS error model for multiposition alignment[J]. IEEE Transactions on Aerospace & Electronic Systems, 1996, 32(4):1362-1366.
[8]Weinberg M S, Kourepenis A. Error sources in in-plane silicon tuning-fork MEMS gyroscopes[J]. Journal of Microelectromechanical Systems, 2006, 15(3):479-491.
[9]孙进, 徐晓苏, 刘义亭,等. 基于逆向导航解算和数据融合的SINS传递对准方法[J]. 中国惯性技术学报, 2015, 23(6):727-732.
[10]邱宏波, 周东灵, 李文耀,等. 基于闭环误差控制器的高精度POS后处理算法[J]. 中国惯性技术学报, 2010, 18(6):691-695.
[11]刘永红, 刘明雍, 谢波,等. 双轴旋转激光捷联惯导系统在线标定技术[J]. 鱼雷技术, 2015, 23(3):218-221.
