一种适应多DSP应用的动基座对准滤波分布式计算方法

陈红兵，丁　伟，张咏兰，邵会兵

(1.海军驻南京地区航天机电系统军事代表室，南京210006; 2.北京控制与电子技术研究所，北京100038)

0　引言

实际工程应用中需要考虑的系统误差复杂，处理的数据信息量大、计算实时性要求高，即使采用最先进的单DSP芯片也无法满足使用要求。因此系统设计上常采取降低计算精度以节约存储和计算空间或者采取更改导航算法的让步软处理方式，但这种折中做法往往会导致导航精度降低和算法复杂度增加，甚至在可观测度低的情况下导致滤波发散，给设计人员带来巨大的工作负担，同时还降低了系统的可靠性[1]。目前，关于动基座对准系统计算负担相关研究较少，主要是根据建模的维度和软件的执行循环次数做笼统估计，不能准确细致计算出算法运行分配负担。赵恒等针对空基传递对准17维建模，根据系统方程离散化过程的理论推导决策降维方案，仿真验证了精度及设计，但并未准确给出单个变量计算复杂度及在系统计算中的优化分配[2]。

本文基于硬件系统与算法设计同步的考虑方式，提出一种适应嵌入式DSP应用的动基座对准滤波分步计算方法，以解决系统实时计算负担的问题。利用嵌入式DSP多处理器并行计算能力强且运行高效的特性，解决单个处理器难以保证滤波实时性的问题；同时算法上在保持导航解算周期不变的前提下，利用多元统计的主成分分析方法计算单个待估变量计算量，提出分布式分配常值性干扰误差和随机性干扰误差方法，以适应性分配给相应DSP处理器运算较大矩阵块及程序步骤，进行分布式计算并缓存矩阵块，最终综合各部分计算结果以达到高精度动基座对准精度。文章首先给出了嵌入式多DSP处理器应用设计，再依次介绍捷联导航系统误差方程及其动基座对准应用，根据主成分分析多元统计法分配系统滤波的分布式计算方法，最后通过一组模拟试验数据验证基于多DSP的分布式计算方法可满足高精度动基座对准要求，同时解决了在线滤波计算负担大的问题[3]。

1　嵌入式多DSP系统的应用

考虑到本文动基座对准滤波采用分布式设计方法，结合预估整体计算量拟采用多块AD公司生产的TS201DSP芯片实现并行计算。该处理芯片是一种高性能静态超标量数字处理器，具有很强的数据处理能力和很高的运算速度，支持32bit、40bit和64bit高精度计算，内部结构上采用双运算模块，支持SIMD处理方式，含相互独立的128位宽数据总线，可以方便地构成高性能的多处理器并行数据处理系统。

1.1　CPCI总线设计

一般数据的逻辑控制及核心处理运算是基于DSP+FPGA+CPCI总线设计的，CPCI总线在电气规则上与PCI总线完全兼容，遵从PCI标准总线数据传输规范，传输速度很高。CPCI采用欧洲标准尺寸，便于设计开发，对于不同板型系统，提供可选择多种插头的连接方式，部分插头信号的使用可以自行定义，相互连接成新的总线，本文基于实际运算采用标准总线设计。

1.2　分布式DSP系统设计

本文采用嵌入式多DSP分布式并行总线结构，避免对总线资源的竞争，适合多分支同步大数据量处理，且每片DSP几乎独立进行数据处理。

图1所示的DSP处理模块由多块ADSP-TS201并行实现，计算节点采用总线紧耦合与分布式并行处理方式相结合，通过Link接口构成两两互连的网络结构。这种并行计算结构的结合，既减少处理器对总线的竞争，又增强了处理器间的数据交换，充分发挥了分布式DSP并行处理能力的优势，灵活运用Link接口方便快速的特点，使得2块并行ADSP-TS101构成的运算体处理能力更快速、更强大。

1.3　分布式DSP系统的并行实现

图2所示为分布式DSP及FPGA系统的并行实现结构，系统中数据存储区用于存储数据处理的中间结果, 是整个处理板的主存储设备。此外由于整个信号处理系统的处理速度很大程度上取决于DSP对外部存储器的读写速度, 因此要求该数据存储区的读写速度必须尽可能地快。基于上述读写速度和存储容量的考虑, 选用一片大容量的高速SDRAM作为数据存储区。同时考虑到动基座对准多分支、多流程功耗大，选用相应的FLASH构成DSP程序存储区。而数据接口收发的缓冲是通过输入缓冲区和输出缓冲区实现，同时保证了处理系统与数据采集系统之间以及主控系统数据交换的缓冲。

首先，FPGA将高速A/ D采集进来的16位原始数据预处理后拼接成64位，然后写入数据缓冲模块，经过采集系统的AD变换后经CPCI总线接口传入TS101 DSP处理区进行分配计算。其次，信号处理板FPGA接收数据后, 将数据写入输入缓存区, 并在完成一帧后给DSP输出中断。最后，当DSP采样到中断后, 从数据缓存区读取数据, 完成处理后, 经过输出缓存区将数据传输给CPCI总线，经过D/A输出使用。

2　捷联导航系统误差方程、滤波系统状态及观测方程

动基座对准是一种多传感器信息融合匹配方法，利用主子惯导的观测误差，通过Kalman滤波来实现导航误差修正。动基座对准系统方程主要是基于姿态误差方程、速度误差方程及位置误差方程建立的，同时需考虑杆臂误差、挠曲形变以及惯性器件误差等多项干扰误差源[4]。

2.1　捷联导航系统误差方程

动基座对准系统方程构建是基于惯性传感器输出信息迭代计算的，一般用到的捷联导航系统误差方程主要有姿态误差方程、速度误差方程及位置误差方程[5-6]。

速度误差方程为

(1)

姿态误差方程为

(2)

位置误差方程为：

(3)

(4)

(5)

2.2　Kalman滤波系统状态及观测矩阵

以主子惯导输出的速度误差和姿态误差为观测量，同时结合上述捷联导航系统误差方程可建立系统状态方程及观测方程[7]。

构建Kalman滤波系统模型：

(6)

式中，X为系统状态变量，A为状态转移矩阵，B为噪声系数矩阵，W为系统噪声，Z为量测匹配量，H为观测矩阵，V为观测噪声(服从白噪声驱动随机分布)。

3　系统滤波分布式计算设计

3.1　主成分分析多元统计原理

传统计算复杂度分析方法仅根据建模维度、理论程序迭代次数粗略分析系统大概计算量，不能准确指出主要影响算法运行待估计变量的复杂度，影响分配变量执行的准确实施。由于每个变量彼此有一定联系，因而系统量的笼统分析在一定程度产生重叠和偏差，本文利用主成分分析思想精确抽取原始建模变量中主要的复杂变量，把粗略系统指标转化为精确主要指标，根据相关特征值分解决策分配方法，同时进一步为优化各误差项建模做准备。

根据系统模型的i维变量对应的i个成分，相应i变量互不相关且按照系统方差阵元素由大到小排列，其中对应第i变量为第i主成分。首先确定系统的协方差阵为P，则P为半正定对称矩阵，按照代数方法求解第i变量特征值λi及其特征向量αi，αi是主成分第i变量相关特征值，而主成分的方差贡献率用以反应信息量大小

(7)

最后要选择几个主要成分，通过信息累计贡献率G(m)来确定

(8)

当累计贡献率G(m)大于系统设定的百分比(δ)，即认为所占系统变量信息比重较大，最后结合建模维度理论和确定的主成分分配主要计算量，同时确定挠曲形变、杆臂误差及时间延迟等干扰误差项的配比。

3.2　杆臂误差、挠曲形变及时间延迟的分配计算

由主成分特征量及海情分析可知，部分变量如杆臂、挠曲形变在各轴向相互独立且误差并未得到完全激励，为保证估计精度同时最大优化系统建模变量，需对必要的杆臂误差、挠曲形变量及时间延迟进行分布式建模补偿。按照作用过程及效果，可统一分为常值误差项和动态误差项，其中常值误差项进行常微分建模或计算补偿，动态误差项根据响应频率进行马尔科夫过程拟合。其中挠曲形变量建模一般按照二阶马尔科夫建模，全状态则极大增加了滤波负担和分配的计算难度，根据分析其中航向挠曲形变对姿态影响较为严重，水平估计则以速度匹配闭合，如此可分离水平、航向姿态估计，同时减小系统计算负担，因而状态建模需扩充航向形变角、航向形变角速率[8-10]。

(9)

杆臂误差及时间延迟的动态作用效果较符合高频噪声特性，一般等效为白噪声过程。因此综合考虑可将常值项误差作为系统预先补偿块，随机干扰作为待估计后续处理块。

(10)

3.3　滤波分布式设计

基于前述主要影响系统估计精度的变量及理论建模可知，确定估计维数的Kalman滤波系统状态转移矩阵及系统噪声计算、滤波递推以及量测更新均存在大量的高维度矩阵运算，若在单DSP系统下采用64bit高精度迭代计算将造成系统巨大的计算负担、占用大量运算资源，短时导航周期内无法完成一次滤波计算的实时性要求。而以单精度32bit运算则会大大节约计算成本，但32bit低精度运算会降低系统的计算精度，尤其是可观测度较低时由于辨识度低、累积误差更大更易引起估计滤波器发散。本节基于嵌入式多DSP的数据处理结构，结合主成分统计的主要计算变量，根据滤波系统各步骤计算的迭代运算量分配计算，各子块存储量可高效传递，最终结合各子块计算结果在一个导航周期内完成滤波修正。

第一步：依据系统状态维数及观测量个数估计各步运算量。

由于矩阵维数决定运算的迭代次数，因而Kalman滤波系统的计算复杂度主要取决于系统状态维数及观测量个数，尤其是高维度的待估计状态量。以一步预测状态方程为例，n维系统方程的计算复杂度约为o(n2)+o(n)，而矩阵相乘的计算频次是o(n3)数量级，且其中失准角变量计算复杂度最高。表1根据复杂度理论计算方法给出13维状态方程相应理论计算频次列表，结果表明系统噪声阵、一步预测均方误差和估计均方误差占用计算资源较多，由此作为后续各步运算量的分布式设计基础。

表1　13维状态方程理论计算复杂度列表

第二步：依据各部分计算复杂度进行分布式设计。

在得出滤波系统各部分计算复杂度的同时，需根据计算机DSP处理芯片存储能力及数量、计算速度以及导航计算的采样周期分配计算资源。单步导航周期内需完成所有步骤矩阵的分步存储及计算，因此分配各子块计算耗时花费应满足如下公式(其中m为分配块数，τ为单步导航计算周期)。

τ1+τ2+τ3+…τm≤τ(m≥1)

(11)

本文考虑20维速度+姿态匹配动基座对准应用，根据估计的计算复杂度结果拟采用4块ADS-TS201DSP处理器存储计算，并按照预分配的计算量将整体估计计算量A按F1(A)、F2(A)、 F3(A)和F4(A)依次分步处理。其中F1(A)项主要进行捷联导航计算及状态转移矩阵计算，F2(A)项主要进行系统噪声阵计算及一步预测状态方程计算，F3(A)项主要进行一步预测均方差及滤波增益计算，F4(A)项主要进行状态估计及估计均方误差计算。其中完成每步分配计算后进行缓存处理，再进行下一步分配计算，直到导航周期时间内完成所有分配计算量后可进行下一周期迭代计算，如图3所示。

4　试验验证

根据上述系统方程及分布式计算原理，设计动基座对准试验验证适应嵌入式多DSP系统的动基座对准滤波分布式设计的正确性。试验按照4块DSP芯片处理器要求搭建数据处理系统，由仿真机模拟一组15min舰船航行中的主基准惯导动态数据，相应地生成一组子惯导原始数据用于捷联解算，将编写的动基座对准软件按分布式设计方法分配嵌入各处理器进行运算，将预先准备的主子惯组数据源注入64bit在线飞控软件运算，得到的对准估计结果如图4～图7所示。其中图6、图7为失准角、安装误差角估计值，图5表明使用滤波计算分布式方法后的计算精度与高精度离线结果误差在5″内，因此本文提出的适应多DSP应用的分步计算方法满足对准精度使用需求。表2所示为64bit计算精度的多DSP处理器飞行控制机在线解算的实际测量耗时列表，对比表1理论计算复杂度可以看出，各计算步骤的量级对应一致，且所有计算时间总和远小于10ms，满足对准算法实时计算的要求，方法设计合理可行。

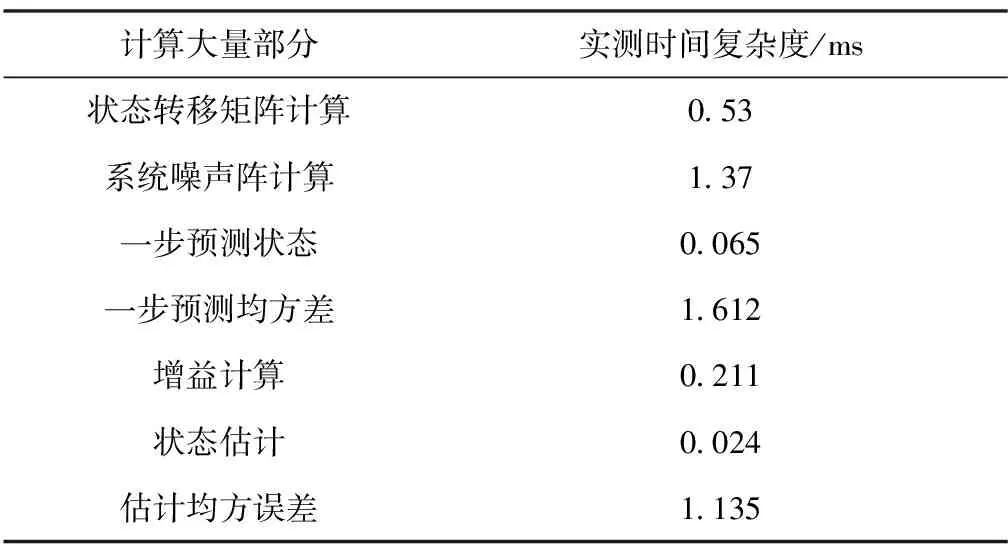
表2　在线飞控计算实际测量耗时列表

5　结论

本文针对动基座对准滤波高维数矩阵计算量大、实时性要求高等问题，利用嵌入式多DSP数字信号处理芯片高时效性运算、通信编程方便、应用程序容易维护等特点，根据对准算法的计算复杂度、耗时测量及算法结构设计分布式滤波方法，保证大量信息并行计算、传递高效简单，同时结合主成分特征分析、航向挠曲形变角扩充分析、杆臂误差及时间延迟分布式优化方法，可满足动基座对准精度及实时性要求。试验结果表明，分布式多DSP结构可以为大数据量计算及并行程序执行提供高效硬件基础，同时保证了最优算法设计的可靠性，为满足动基座对准滤波解决实时性、高效运算提供一条适用途径。后续工作将进一步探索在其他导航工程中，分布式软硬件设计的应用方法。

[1]程明文, 刘勇志, 徐显强. 潜射导弹捷联惯导系统传递对准技术研究[J]. 鱼雷技术, 2010, 18(5):367-370.

[2]赵恒, 苏永清, 叶萍. 快速传递对准滤波器设计及其计算复杂度分析[J]. 弹箭与制导学报, 2011, 31(3):31-34.

[3]樊荣. 捷联惯导系统传递对准方法研究及其仿真[D]. 南京: 南京理工大学, 2006.

[4]代传堂. 基于多DSP的高速通用信号处理平台的设计与研究[ D] . 西安: 西安电子科技大学, 2006.

[5]郑辛, 武少伟, 吴亮华. 导弹武器惯导系统传递对准技术综述[J]. 导航定位与授时, 2016, 3(1):1-8.

[6]白成萌, 杨功流. 王丽芬, 等. 舰载机动基座快速对准方法研究[J]. 导航定位与授时, 2016, 3(1):13-18.

[7]陈国良. 并行计算——结构、算法、编程[M]. 北京: 高等教育出版社, 1999.

[8]AIAA. Rapid transfer alignment for tactical weapon applications[C]∥Proceedings of AIAA Guidance，Navigation and Control Conference，1989：1290-1300.

[9]秦永元. 惯性导航[M]. 北京：科学出版社，2006：327-330．

[10]李蓓. 捷联惯导传递对准可观测性分析[D]. 哈尔滨：哈尔滨工程大学，2008：45-61．