基于神经网络的生产线路径优化模型研究

李彬，张雷

（重庆交通大学，重庆 400074）

装配线上的螺母问题就是在每条装配线上用一个机械手去紧固螺母，机械手从当前位置开始，依次移动到每一个螺母处完成拧紧的工作，最后返回初始位置。要想让除修复机器以外的成本尽量少，最好的办法就是减少辅助工时。加工辅助工时就是非加工时间，包括装夹、拆卸产品、去毛刺、涂防锈油，等等。在实际工作中，机械手移动速度不能过快，否则会产生大的惯性，无法保证螺母拧紧的质量。那么，在速度一定的情况下，找到最短路线，让机械手沿着这条路线来移动，从而大大缩短所需时间是一个很有效的方法。

目前，国内采用的大多数方法存在一个问题，即规划算法本身具有局限性，容易陷入局部最优，优化效果不明显。因此，本文采用优化的蚁群算法求解[1]。

1 模型的建立

“旅行商问题”（TSP问题）是建模领域一个经典的问题，大意是一名推销员拜访多个地点时，要找到在拜访每个地点一次后再回到起点的最短路径。从对TSP问题的描述中可以看出，螺母的装配路径优化问题在数学本质上与TSP问题是相通的，都是要求解最短路径。螺母装配问题中的每个螺母就相当于TSP问题中的城市，因此，求解了该模型就相当于求解了螺母装配问题。

2 求解的基本步骤

2.1 选择算法

求解上述问题的算法有很多种，但是，大多都存在求出的解是局部最优而非全局最优的问题。本文采用蚁群算法求解模型，大大提高了算法的效率，易于找到全局最优[2-3]。

2.2 基本原理[4]

在蚂蚁转移过程中，信息素会以一定速度挥发，假设参数ρ表示挥发程度，于是有m只蚂蚁完成一次遍历过后，两两城市之间路径上的信息素更新为：

2.3 基本步骤

运用蚁群算法解决螺母装配问题一般要经过以下几个步骤：①初始化参数。初次计算时，需要对模型中有些参数赋初值，比如蚂蚁数量m、信息素重要因子α、启发函数重要程度因子β、信息素挥发因子ρ等。②初始化解空间。计算之初，将所有的蚂蚁随机放到不同的出发点，对每个蚂蚁按照式（1）计算其下一个将要去的城市，直到访问完所有的城市。③更新信息素。计算每个蚂蚁走过的路径长度Lk，记录当前最小路径，同时根据式（2）、式（3）更新各条路径上的信息素。④判断结束与否。例如，当前迭代次数iter＞iter_max，程序结束，输出最优解，否则返回步骤③。

3 螺栓装配问题的优化[5-6]

本文针对生产过程中典型的内圈8个、外圈8个排列的螺栓装配问题进行求解，如图1所示。

3.1 计算螺栓间距离

根据各个螺栓的坐标，利用MATLAB编程计算出两两螺栓之间的距离，从而得到对称的矩阵。由于对角线上的数据均为0，而计算启发函数的时候dij为分母，所以，将对角线上的数据修正为很小的正数10-4.

3.2 初始化参数

计算之初，令m＝31，α＝1，β＝5，ρ＝0.1，Q＝1，η＝1/D，iter_max＝200，iter＝1.

3.3 迭代求解

构建解空间，计算每个蚂蚁走过的距离，根据式（2）、式（3）实时更新路径上的信息素浓度，经过循环迭代，记下最优解。

3.4 结果分析

程序运行结果如图2所示。经过计算，最短距离为17.414，最短路径为5-4-12-11-3-2-10-9-1-8-16-15-7-6-14-13-5，用此算法规划出的路径比实际中先拧紧外面一圈再拧紧里面一圈所经过的路径长度少了1.6，一道装配工序就减少了将近10%的时间，由此可见效率大大提高。

4 参数的影响

对比了10组不同的蚂蚁个数下距离平均值的变化，发现当蚂蚁个数为45时平均路径最短，此时最短路径为17.413.根据控制变量的思想，还可讨论信息素重要程度因子α、启发函数重要程度因子β、信息素挥发因子ρ对结果的影响。由于原理与蚂蚁个数对结果的影响相同，所以此处不再赘述。

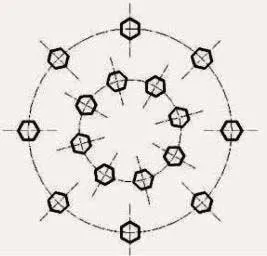
图1 典型螺栓装配图

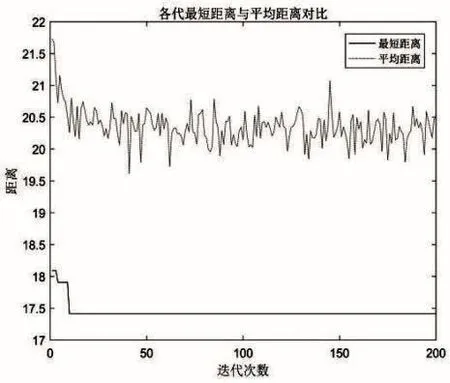
图2 优化过程中的装配路径距离变化

5 结束语

本文将神经网络中的蚁群算法应用到螺栓装配的路径规划问题上，颠覆了传统的八边形位置分布的螺栓装配顺序，优化了螺栓装配的路径，大大提高了加工装配效率。在计算求解过程中，通过软件检验文中的算法，具有良好的精度和稳定性，且收敛较快，所以，有一定的合理性。因此，本文的研究也为实际工作提供了一定的参考价值。另外，本文的算法可以应用到其他领域，例如数控加工中的打孔问题，具有推广价值。

参考文献：

［1］杨剑峰.蚁群算法及其应用研究［D］.杭州：浙江大学，2007.

［2］秦玲.蚁群算法的改进与应用［D］.扬州：扬州大学，2004.

［3］陈建玲.基于蚁群算法的优化问题研究［D］.大庆：大庆石油学院，2007.

［4］郁磊.MATLAB智能算法30个案例分析［M］.北京：北京航空航天大学出版社，2015：205-212.

［5］谢庆生，尹健，罗延科.机械工程中的神经网络方法［M］.北京：机械工业出版社，2003：159-162.

［6］钟经农.神经网络理论在CAPP系统中的应用［D］.长沙：湖南大学，1996.