基于数值模拟的流体中曲面受力计算分析方法研究
2018-04-12黄膺翰颜剑波
李 翔,黄膺翰,颜剑波,李 璜
(中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410116)
1 研究背景
在工程领域,拦污栅、隔水帷幕、弧形闸等外观近曲面的工程设施具有形态复杂、受力计算困难、受力分布计算量大的特点,现有的计算方法多将这些曲面的受力分为静水压力和动水压力2方面求解。在求解静水压力时,认为压力符合静压分布,如果曲面一侧为流体,一侧为大气,则静水压力计算公式为:
式(1)中:ps为静水压强;ρ为流体密度;g为重力加速度;h为水深。
如果将曲面置于流体中,两侧都有流体,则认为曲面受到的静水压力为两侧静水压力之差,即:
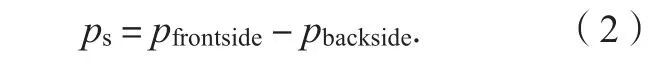
式(2)中:pfrontside为曲面正面的静水压强;pbackside为曲面背面的静水压强。
该方法假设静水压力沿垂向变化,在水平方向相等,因此,仅适用于静水压力水平方向差异比较小的情况。如果流体在水平方向由于盐度、含沙量、温度等因素分布不均,则会呈现出密度差异,引起静水压力在水平方向的变化,那时,采用该方法难以正确求解。
在求解动水压力时,多以动量方程求解,即:
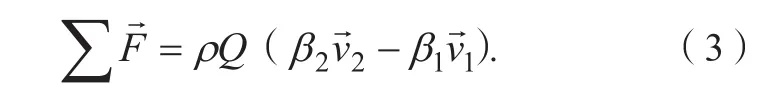
该方法可求解简单情况下曲面承受的总动水压力受力,但是,不能精细求解动水压力的分布情况。另外,该方法也难以求解绕流等复杂流态下曲面的动水压力。
随着数值模拟计算应用的普及,当前部分商业数值模拟软件也具有曲面受力计算的功能,但是,这些软件存在以下2个缺陷:①部分商业软件仅可输出曲面的整体受力,不能得到曲面的受力分布;②当曲面至于流体中,两侧均有流体时,如果部分曲面的网格正面为流体,背面为固体,则该网格正面压力会被计算为静水压力与动水压力之和,背面压力会被识别为无压力。而在实际情况下,如果曲面贴向固体,会受到固体的顶托力,以平衡流体带来的压力。因此,这种算法与实际受力不符,当水深较深时,使用这个方法会导致非常大的计算误差。
随着工程技术的发展,对水工建筑物的受力分析提出了更高的要求,但现有的曲面受力计算方法已难以满足工程应用的需要。针对上述技术问题,本文提出了一种能在数值模拟计算结果的基础上精确求解和分析流体中复杂曲面受力分布的计算方法。该计算方法计算逻辑与编程语言相符,能有效解决曲面受力分布计算量大的问题。
2 虚拟面的概化
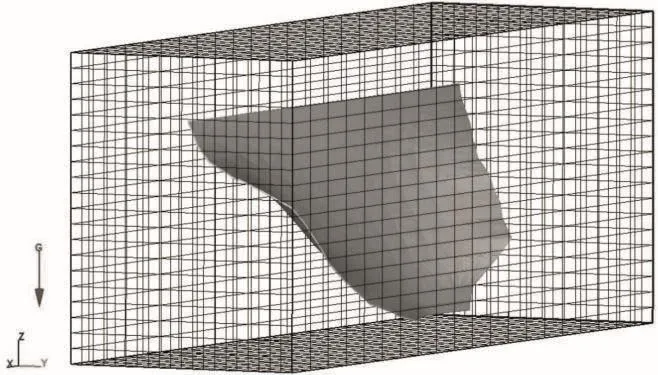
图1 网格划分示意图
如图1所示,在数值模拟时,模拟空间会被划分为若干排列有序的网格。如果模拟网格为结构化网格,网格排列为矩阵形式。空间中的每一个网格都会被赋予坐标根据其坐标(x,y,z)的排序,赋予序号编号(i,j,k)。其中,i为网格沿y方向的序号,j为网格沿x方向的序号,k为网格沿z方向的序号。网格与网格之间存在网格交界面。如图2所示,在网格解析实体曲面时,模型会根据网格尺寸和类型将实体的曲面(红色曲线)概化为若干平面组成的近似于曲面的复杂形态,而这些平面即为特殊的网格交界面(以下称“虚拟面”)。当整个模型在迭代求解时,没有被概化为曲面的网格交界面允许水流通过,而被概化为曲面的虚拟面不允许水流通过。也就是说,在模型计算时,这些虚拟面就是曲面。因此,求出这些虚拟面的受力便能求解出曲面的受力。
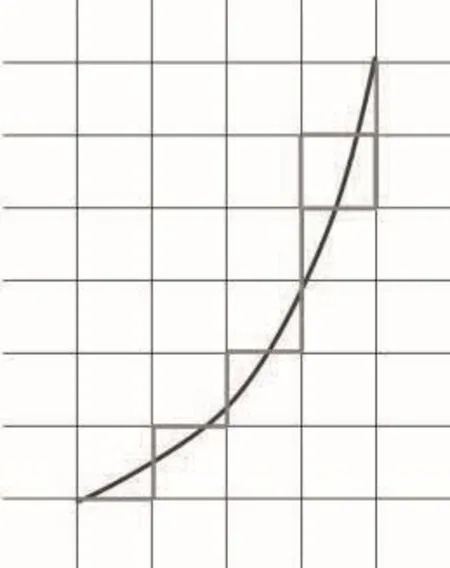
图2 曲面概化方法示意图
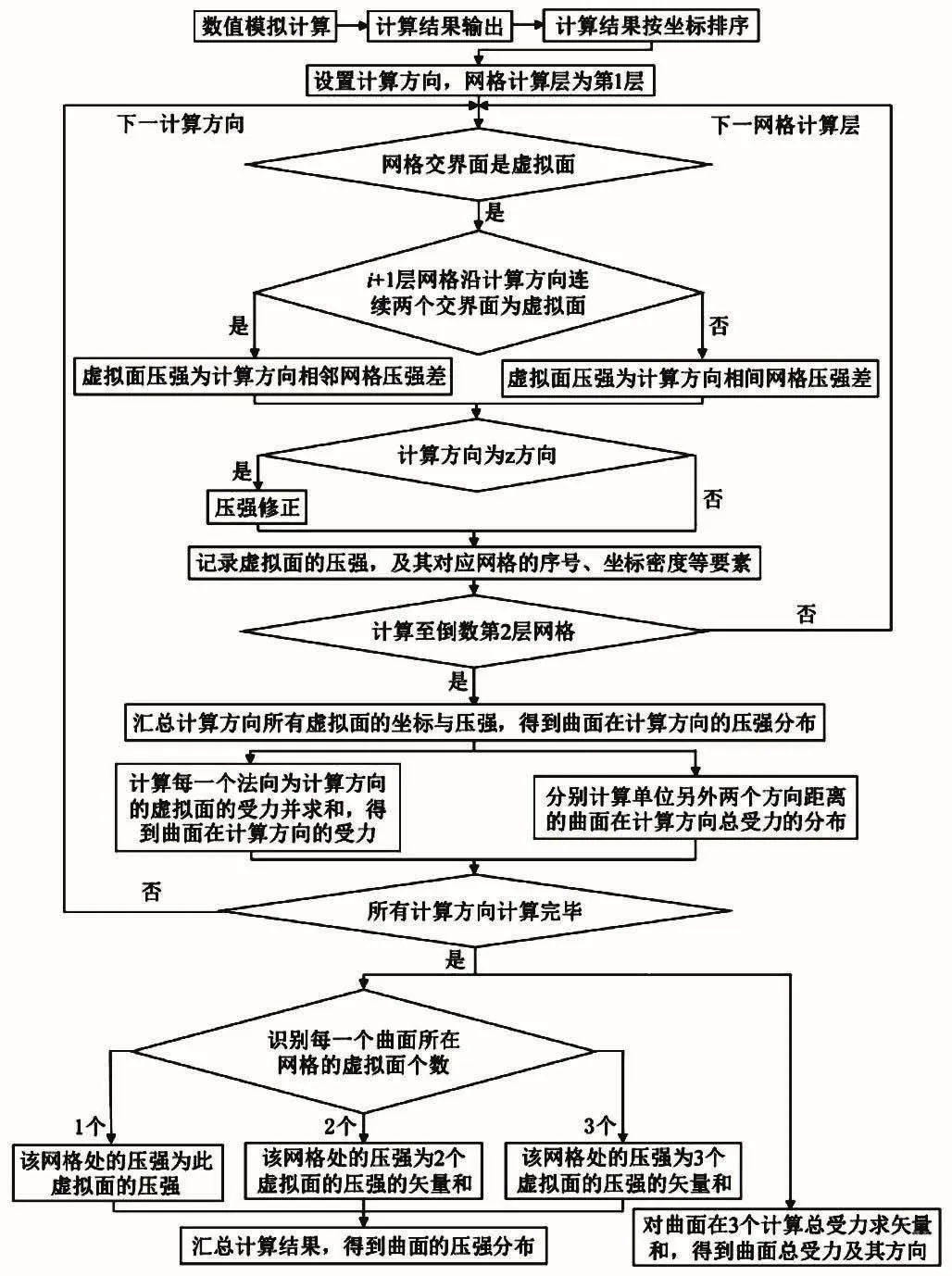
图3 计算逻辑图
3 计算思路
对于结构化网格,曲面周围流场的数值模拟计算结果主要为位置与数据的关系。对于每一个网格,都有表示位置的坐标和对应的比如流速、压强等数据。由于虚拟面上的压强差、流速梯度等参数具有较大的区别,可作为虚拟面的特征之一。因此,按照一定的顺序,根据曲面周围的网格计算出所有网格的网格交界面后,可根据计算结果识别出虚拟面,对其进行更精细的受力计算分析。此即为本方法的计算思路,详细计算逻辑如图3所示。
4 计算步骤
本计算方法的计算步骤如下:
步骤1:采用数学模型计算曲面周围流体的流场、压力场和密度场。
步骤2:以网格坐标与网格要素(压强、密度等)一一对应的形式导出数学模型计算结果。
步骤3:将x方向、y方向网格点对应压力、密度、网格类型按照坐标升序排列,垂向网格点对应压力、密度、网格类型按坐标降序排列。
步骤4:对于任意第i层网格,将该层的每一个网格与相邻的第i+1层对应网格的压强值相减,即可得到第i层网格第i+1层网格所有网格交界面(不论网格交界面是否为虚拟面,均要进行计算)在y方向的压强差△px,i,j,k,即:
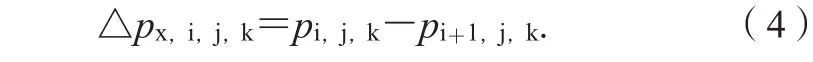
式(4)中:△px,i,j,k为编号为(i,j,k)的网格在 x 方向网格交界面上的压强差;pi,j,k为编号为(i,j,k)的网格在网格中心处的压强值;pi+1,j,k为编号为(i+1,j,k)的网格在网格中心处的压强值。
步骤5:识别第i层与第i+1层每一个网格的网格类型,以及对应网格交界面的压强差△px,i,j,k,判定该交界面是否为幕墙虚拟面。如果交界面是曲面概化形成的虚拟面,则记录下该交界面的位置与压强差。
步骤6:检查是否曲面概化时,出现图2所示的灰色折线所示情况,即沿计算方向的连续2个面均为虚拟面。因此,将第i层网格与第i+2层网格对应的压强值相减,并记录下该交界面的位置与压强差,该步骤计算公式为;
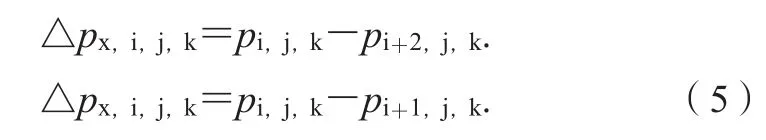
式(5)中:pi+2,j,k为编号为(i+2,j,k)的网格在网格中心处的压强值。
步骤7:一次令i=1,2,…,n,沿x方向对每一层网格做步骤4~步骤6,即可汇总到曲面在x方向投影的受力分布,即每一个法向为x方向虚拟面上的压强差△px,i,j,k.
步骤8:对于所有法向为x方向的虚拟面,按式(6)可计算出单位y方向距离的曲面在x方向的总受力分布,即:
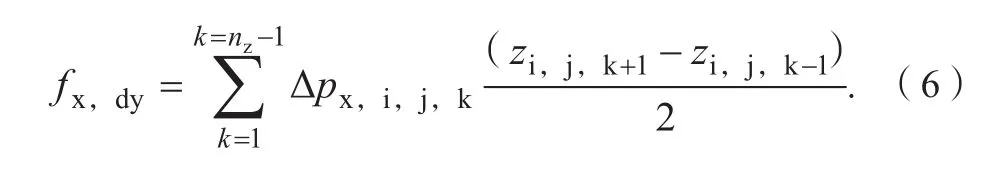
式(6)中:fx,dy为法向为x方向的虚拟面在单位y方向距离的曲面在x方向的总受力分布;nz为计算区域在z方向的网格总数。
步骤9:对所有法向为x方向的虚拟面,按照式(7)可以计算出单位z方向距离的曲面在x方向总受力的分布,即:
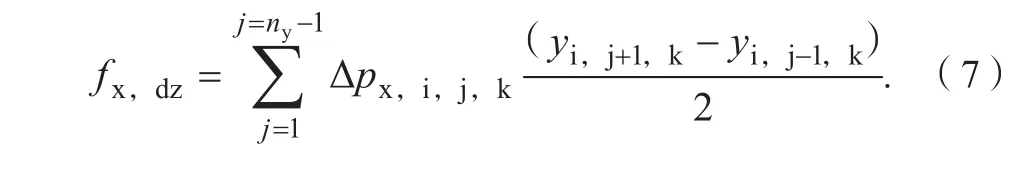
式(7)中:fx,dz为单位z方向距离的曲面在x方向的总受力分布;ny为计算区域在y方向的网格总数。
步骤10:按照式(8)计算出每一个法向为x方向的虚拟面上的受力,即:
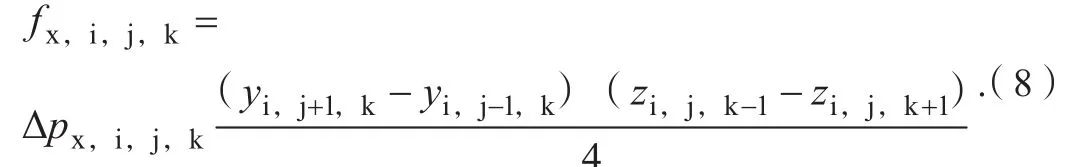
式(8)中:fx,i,j,k为编号为(i,j,k)的虚拟面在 x 方向上的受力;yi,j+1,k为编号为(i,j+1,k)的网格在网格中心处的 y 坐标值;yi,j-1,k为编号为(i,j-1,k)的网格在网格中心处的 y 坐标值;zi,j,k-1为编号为(i,j,k-1)的网格在网格中心处的 y 坐标值;zi,j,k+1为编号为(i,j,k+1)的网格在网格中心处的y坐标值。
对所有法向为x方向的虚拟面上的受力求和,即可得到整个曲面在x方向的总受力Fx,即:
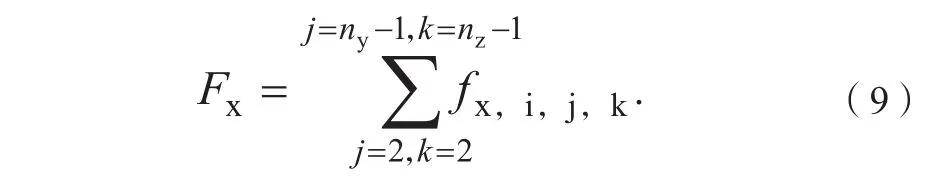
式(9)中:Fx为曲面在x方向的总受力;nz为计算区域在z方向的网格总数。
步骤11:沿y方向对每一层网格作与步骤4~步骤11相似的操作,可汇总到曲面y方向的压强差分布,即每个法向为y方向虚拟面上的压强差△px,i,j,k.同时还可计算每个法向为y方向的虚拟面的受力fy,i,j,k,法向为y方向的虚拟面在单位x方向的总受力分布fy,dx,法向为y方向的虚拟面在单位z方向的总受力分布fy,dz,曲面在y方向的总受力Fy.
步骤12:考虑到每一个网格的压强值为网格中心处位置的压强值,而非网格交界面上的压强值,对于x方向和y方向,在一个网格尺度内,网格中心处的压强值与网格边沿的压强值无明显变化,其误差可以忽略。但是,在z方向,静水压力沿z方向有明显变化,会给计算带来明显误差。因此,在沿z方向对每一层网格作与步骤4~步骤7相似的操作时,需对步骤4的计算公式进行如下修正:
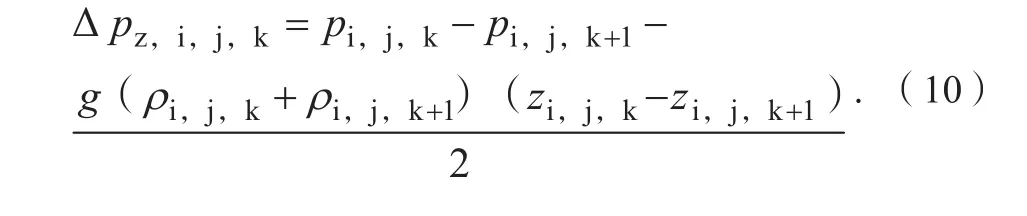
式(10)中:△pz,i,j,k为编号为(i,j,k)的网格在 z 方向网格交界面上的压强差;pi,j,k+1为编号为(i,j,k+1)的网格在网格中心处的压强值;ρi,j,k为编号为(i,j,k)的网格在网格中心处的密度值;ρi,j,k+1为编号为(i,j,k+1)的网格在网格中心处的密度值;zi,j,k为编号为(i,j,k)的网格在网格中心处的 z 坐标值;zi,j,k+1为编号为(i,j,k+1)的网格在网格中心处的z坐标值。
同理,还需对步骤6的计算公式进行修正,即:
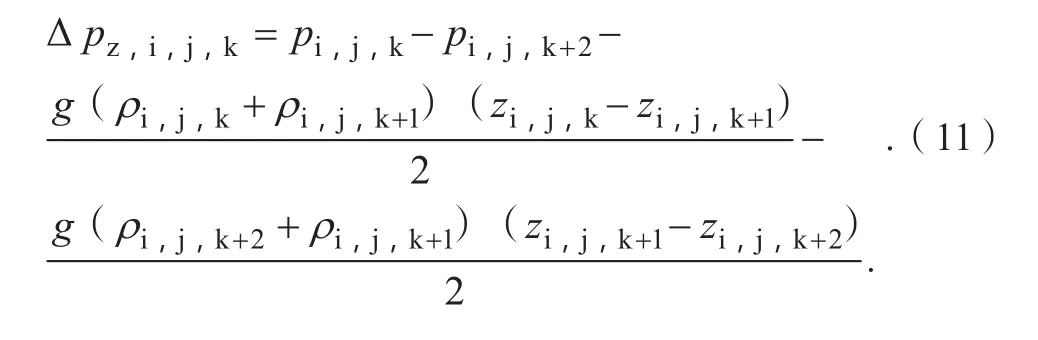
式(11)中:pi,j,k+2为编号为(i,j,k+1)的网格在网格中心处的压强值;ρi,j,k+2为编号为(i,j,k+2)的网格在网格中心处的密度值;zi,j,k+2为编号为(i,j,k+2)的网格在网格中心处的z坐标值。
沿z方向对每一层网格采用修正后的公式进行与步骤4~步骤11相似的操作,可以汇总到曲面z方向的压强差分布,即每一个法向为z方向的虚拟面上的压强差△pz,i,j,k.同时,还可以计算得到每个法向为z方向的虚拟面的受力fz,i,j,k,法向为z方向的虚拟面在单位x方向的总受力分布fz,dx,法向为z方向的虚拟面在单位y方向的总受力分布fz,dy,曲面在z方向的总受力Fz.
步骤13:对于曲面所在网格,如果网格仅有一个方向的虚拟面(例如x方向,其他方向与之类似),则该曲面在该网格处的压强为此虚拟面的压强,即:
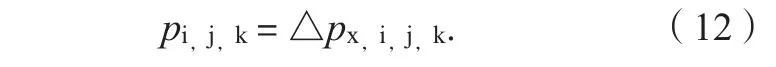
式(12)中:pi,j,k为曲面在编号(i,j,k)网格处的压强。
如果网格含有2个虚拟面,则曲面在该网格处的压强为2个虚拟面(例如x方向和y方向)的压强之和,即:
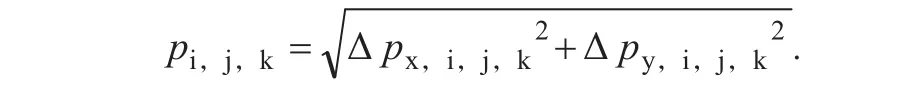
如果网格含有x方向、y方向、z方向的虚拟面,则曲面在该网格处的压强为3个虚拟面(例如x方向和y方向)的压强之和,即:
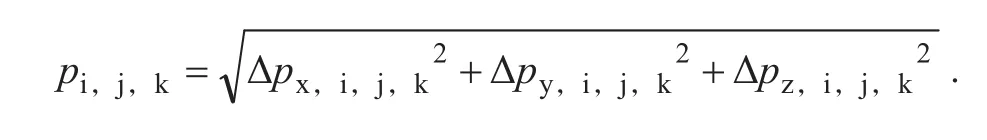
由此,可以得到曲面的压强分布。
步骤14:对曲面在x方向、y方向、z方向的总受力进行求和,可得到曲面的总受力为:
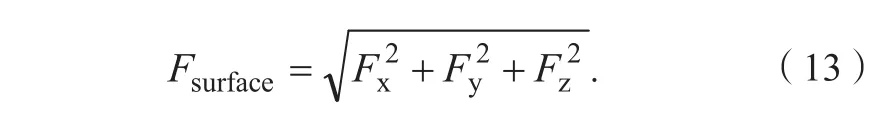
式(13)中:Fsurface为曲面总受力。
5 结论
针对当前工程领域内流体中曲面受力计算分析方法存在的不足,本文提出了一种能在数值模拟计算结果的基础上精确求解和分析流体中复杂曲面受力分布的计算方法。该计算方法计算逻辑与编程语言相符,能有效解决曲面受力分布计算量大的问题。
6 展望
受文章篇幅限制,在此仅提出流体中曲面受力计算分析方法,该方法在工程上的应用将另行他文介绍。
