开关转换器动态分析采用快速分析技术
2018-04-11
如果采用网格节点(mesh-node)分析能很好地求解电路的传递函数,那么立即获得一个有意义的符号公式通常是不可能的,需要额外的工作才能得出。应用经典的分析技术来获得所谓的低熵表达式,即分数形式,从中您可识别增益、极点和零点,往往导致如Middlebrook博士曾在他的参考文献[1]、[2]中提到的代数失效(algebraic paralysis)。在此,快速分析电路技术(FACTs)可帮助您基于在大学里学到的东西而扩展,以大大简化分析。通过使用FACTs,不仅加快您的执行速度,而且最终结果将以有序的多项式形式出现,通常无需进一步的因子分解工作[3-4]。
本文首先介绍后文用于确定开关转换器的控制到输出传递函数的FACTs。这个主题很大,在此我们只谈及表面,希望激励您进一步挖掘这个主题。我们选择了电压模式耦合电感单端初级电感转换器(SEPIC)工作于非连续导电模式(DCM)。PWM开关[5]将用于形成小信号模型。
快速分析技术(FACTs)简介
FACTs背后的基本原理在于电路时间常数的确定τ=RC或τ=L/R,此时在两种不同的条件下观察所研究的电路:当激励信号降至0时和响应清0时,通过使用这种技术,您将体会到确定特定传递函数有多快和直观。基于这种方法的分析技术始于几十年前,如参考文献[6]、[7]中记载的。
传递函数是一种数学关系,它把激励信号、激励物和由这种激励产生的响应信号联系起来。如果我们考虑一个线性时不变(LTI)系统无延时,具有静态增益H0,例如开关转换器的线性理想功率级,其连接控制信号Verr(激励)和输出Vout(响应)的传递函数H可表示为:
(1)
首项H0是系统在s = 0评估表现出的增益或衰减,该项将带传递函数的单位(或维度),如果有的话。如果响应和激励都用伏特表示,在此表示为Verr和Vout,H是没有单位的。分子N(s)控制传递函数的零点,数学意义上,零点是函数幅值为0的根。通过FACTs,我们用数学抽象思维轻松地揭开这些零点。我们不会像通常在谐波分析(s=jω)中所做的仅仅考虑在s平面的垂直轴,而是覆盖考虑到负数根的整个平面。因此,如果电路存在零点,将表现为当输入信号调到零角频率sz时,无信号的输出响应。在这种情况下,在变形的电路中的一些阻抗阻挡了信号传播,响应为0,尽管存在激励源:当变形的电路在s=sz点被激励时,在信号路径的串联阻抗趋于无穷或分支将该激励分流到地面。请注意,这种方便的数学抽象通过观察提供了巨大的帮助来找到零点,通常无需写一行无源电路的代数。图1提供了简单的流程图,详细介绍了过程。关于这种方法的更多细节见参考文献[8]。

图1 这个流程图将指导您用最简单的方法确定零点,在观察无用时,将需要进行双重抵消注入或NDI
分母D(s)由电路自然时间常数构成。通过设置激励信号为0和确定从电路中临时移除的所考虑的电容或电感“所示”的阻抗,来得出这些时间常数。通过“观察”,可想象把一个欧姆表置于暂时移除的储能元件(C或L),并读取它显示的电阻。这其实是个相当简单的运用,正如图2中的第二个流程图所详述的。

图2 该流程图解释了用于确定电路时间常数的方法
看到图3是一个涉及注入源的一阶无源电路加偏压于左边网络。输入信号Vin通过网格和节点传播形成所看到的电阻R3上的响应Vout。我们感兴趣的是导出连接Vout和Vin的传递函数G。
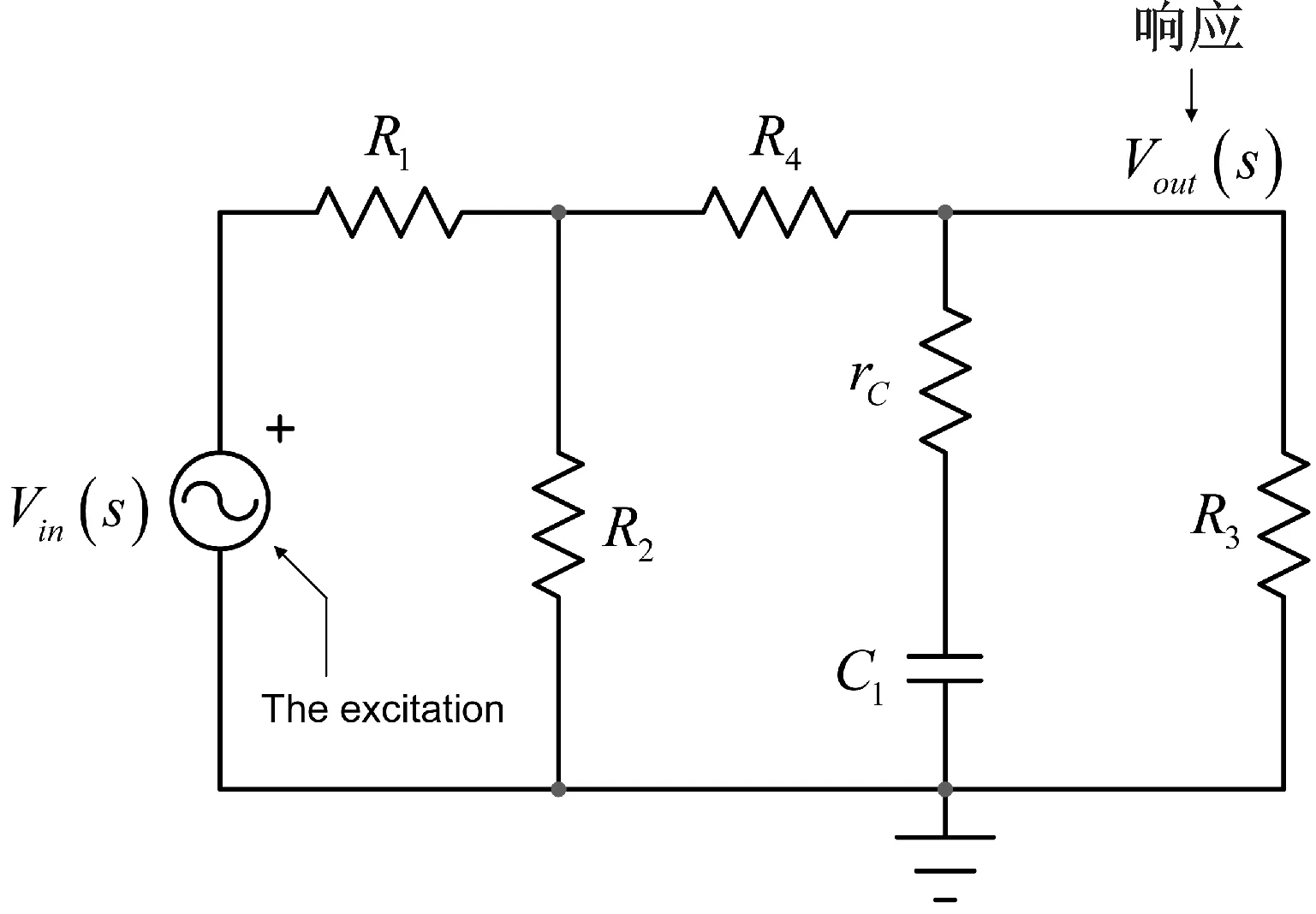
图3 确定电路的时间常数需要将激励源设为0,并观察从电路中暂时移除的能量存储元件所提供的电阻
为确定本例电路的时间常数,将激励源设为0(由短路代替0 V电压源,开路代替0 A电流源),拆下电容器。然后,连接一个欧姆表来确定电容器端提供的电阻。图4指导您进行这些步骤。
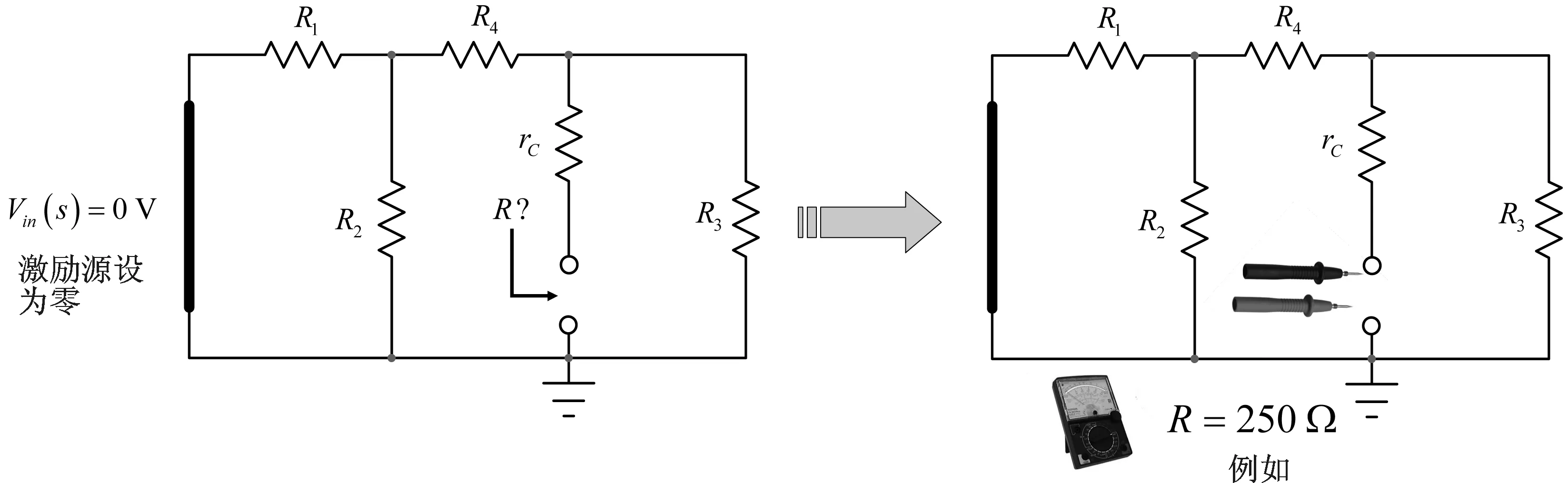
图4 由短路代替0V源后确定电容器端的电阻
如果用图4的做法,您“看到” R1与R2并联后与R4串联,所有这些与R3并联后与rC串联。该电路的时间常数只通过R和C1即可计算得出:
τ1=[rC+(R4+R1||R2)||R3|C1
(2)
可证明第一阶系统的极点是其时间常数的倒数。因此:
(3)
现在,s=0时该电路的准静态增益是多少?在直流条件下,电感器短路,电容器开路。把这概念应用于图3的电路,绘制成如图5所示的电路。想象在R4前断开连接,会看到一个含R1和R2的电阻分压器。R2上的戴维宁(Thévenin)电压为:
(4)
输出电阻Rth是R1与R2并联的值。因此完整的传递函数涉及到电阻分压器(由与Rth串联的R4和加载的R3所构成)。rC是断开的,由于电容C1在这直流分析中被移除。因此:
(5)
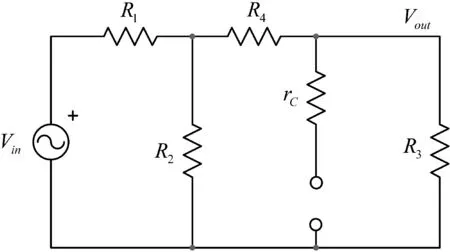
图5 断开直流电路中的电容器,计算简单的电阻配置的传递函数
基本就是这些了,我们正错过零点。在前文提到,零点通过阻断激励信号的传播而在电路中表现出来,产生一个无信号的输出响应(见图1)。若我们考虑一个变形的电路,其中C1由1/sC1代替,如图6所示,当激励源加偏压于电路,有什么特定的条件意味着无信号响应?无信号响应只意味流过R3的电流为0。这不是短路,而是相当于虚拟的接地。
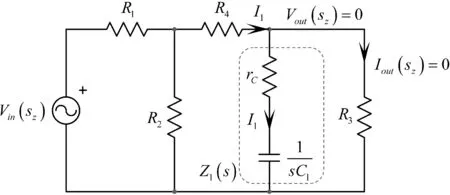
图6 在这变形的电路中,当串联的rC和C1转化为变形的短路,响应消失,R3中无电流流过
如果在R3中没有电流,那么串联的rC和1/sC1转化为短路:
(6)
根sz是我们想要的零点位置:
(7)
从而有:
(8)
现在我们可组合所有这些结果,形成以图3电路为特征的最终的传递函数:
(9)
这就是所谓的低熵表达式,从中您可立即识别静态增益G0、极点ωp和零点ωz。高熵表达式将在考虑阻抗分压器时通过施加大规模外力到原来的电路来获得,如:
(10)
您不只在推导表达式时可能会出错,而且将结果格式化到如式(9)这样需要更多的精力。另外,请注意,在这个特定的例子中,在写式(9)时我们没有写一行代数。如果我们后来发现一个错误,那么很容易回到一个单独的图纸并单独修复它。式(9)的校正很简单,现尝试对式(10)进行相同的修正,您可能会从头开始。
FACTs应用于二阶系统
FACTs同样适用于n阶无源或有源电路。通过计算状态变量是独立的储能元件的数量来确定电路的阶数。若我们考虑一个具有有限的静态增益H0的二阶系统,其传递函数可表示如下:
(11)
当H0带传递函数的单位,那么N:D的比值是没有单位的。这意味着a1和b1的单位是s。当a1无信号响应,b1的激励源为0,可将确定的时间常数相加。对于二阶系数a2或b2,维度是时间的平方[s2],将时间常数结合为一个产物。然而,在这时间常数产物中,您重用了已经确定为a1或b1的一个时间常数,而二阶时间常数的确定需要一个不同的符号:
(12)
在这个定义中,设置标号出现在“幂” 中的储能元件处于高频状态(电容被短路,电感被开路),当我们暂时从电路中移除二阶元件端(参见下标),您可从中确定电阻。当a2必须为无信号的输出和b2的激励源减为0时,可以运用此法。当然,当观察有用时,它总是最快和最高效的得出N的方法。乍一看有点难以理解,但没有什么不可克服的,我们用几句话解释您就会明白。
图7是一个经典的二阶滤波器,用于确定在连续导通模式(CCM)中工作的电压模式降压转换器的输出阻抗。阻抗是连接一个激励信号Iout与响应信号Vout的一个传递函数。此处,Iout是已安装的测试生成器,而Vout是其两端产生的电压。要从式(11)中确定各种系数,我们可按照图2的流程图,从s=0开始,如图7所示,电感短路,电容开路。该电路是简单的,电流源的电阻R0不过是rL和Rload简单的并列组合:
R0=rL||Rload
(13)
这个电路中有零点吗?我们看看图8所示的变形电路。当激励源电流Iout调为零角频率sz时,什么样的元件组合将使响应Vout为0。我们可发现两个变形的短路涉及rL-L1和rc-C2。

图7 工作于CCM的降压转换器的输出阻抗的确定是一个很好的例子,演示了FACTs如何简化分析

图8 如果阻抗Z1或Z2转换为短路,响应Vout为无信号输出
立即确定这两个阻抗的根:
(15)
因此分母N(s)表示为:
(16)
分母D(s)的一阶系数b1是由L1两端的阻抗提供,而C2处于直流状态(开路),有τ1,然后看驱动C2而L1设置为直流状态(短路)时的阻抗,得出τ2。如图9所示,从该草图可立即得出b1的定义:
C2[(rL||Rload)+rC|
(17)

图9 在选定的组件终端中,当第二个组件处于直流状态时,您会得出阻抗为多少?
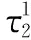
(18)
现在我们用所有的成分来组合最终的传递函数,定义为:
Zout(s)=(rL||Rload)×
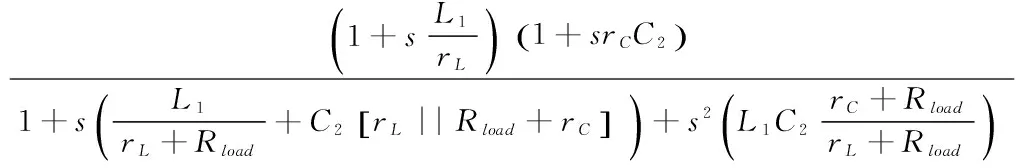
(19)
我们已经确定了这个传递函数,而没有写一行代数,只是把该电路拆分为几个简单的草图个别解决。此外,正如预期的那样,式(19)已经是一个规范的表达式,可以轻易地看到一个静态增益、两个零点和一个可用谐振分量ω0和品质因数Q进一步整理的二阶分母。如果不是迅速考虑Z1、Z2和Rload的并联组合,我们不可能得到这一结果。
采用FACTs,通过观察可导出传递函数,特别是对于无源电路。由于电路复杂,包括电压或电流控制源,观察
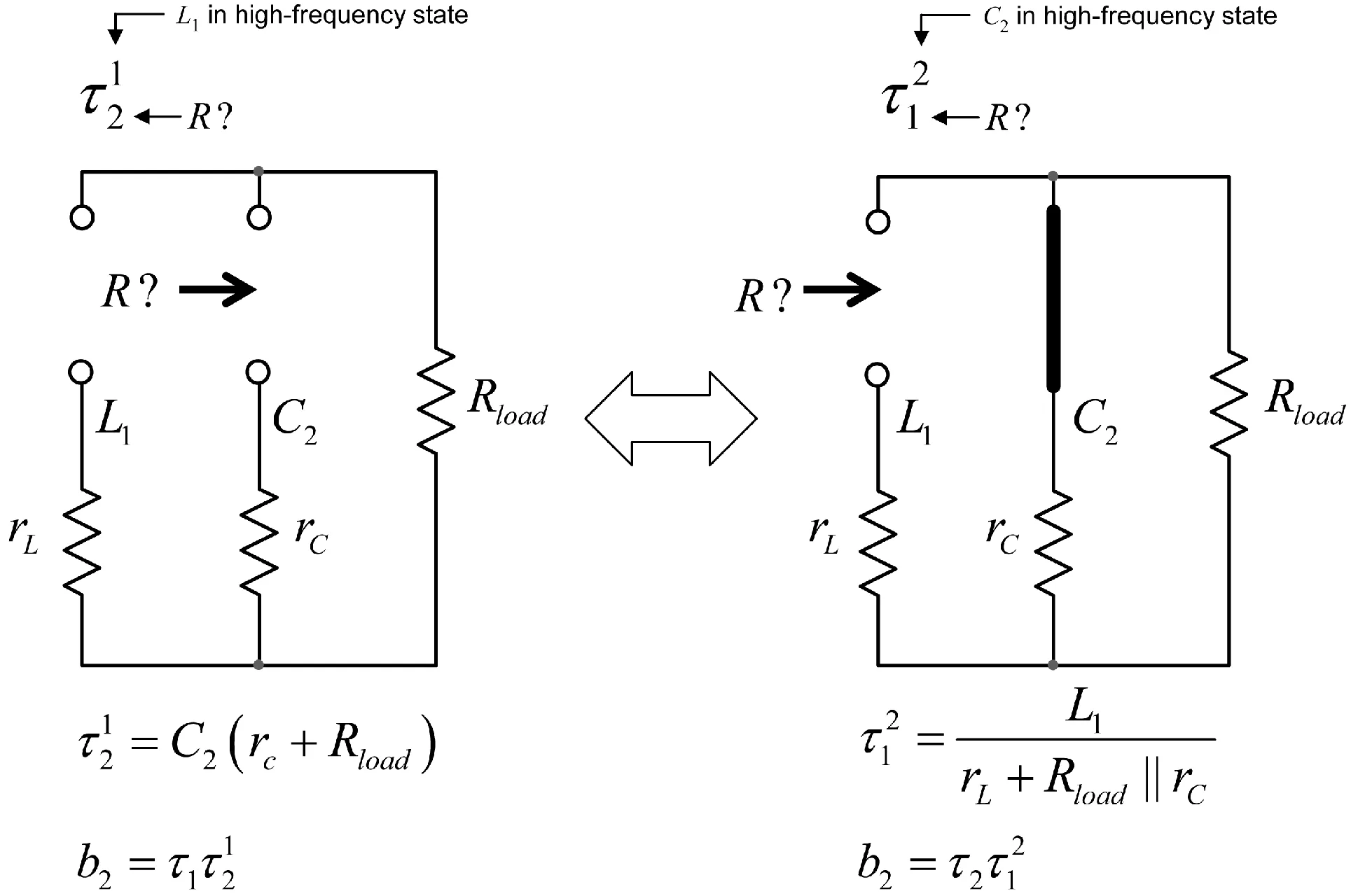
图10 在选定的组件终端中,当第二个组件处于高频状态时,您会得出阻抗为多少?
起来没那么明显,您需要利用经典的网格和节点分析。但FACTs提供了几个优点:由于将电路拆分为用于确定最终的多项式表达式系数的小的单个草图,因此如果在最终的表达式中发现一个错误,总是可以回到一个特定的绘图并个别修正。此外,当确定与传递函数的ai和bi相关的项时,自然会得到一个多项式表达式,而不用投入进一步的精力来收集和重新排列这些项。最后,如参考文献[4]所述,在复杂的无源和有源电路中,SPICE对验证个别极点和零点的计算有很大帮助。
工作于DCM的带耦合电感的SEPIC
SEPIC是一种流行的结构,常用于输出电压必须小于或大于输入的应用,不会像采用Buck-Boost转换器那样损失极性。SEPIC可采用耦合或非耦合电感工作在连续导通模式(CCM)或非连续导通模式(DCM)。参考文献[9]中探讨了耦合电感的好处,这里不作讨论,我们的兴趣在于确定耦合电感的SEPIC 在工作于DCM时的输出到控制的传递函数。图11代表参考文献[10]中所述的自动切换电压控制模式的PWM开关和采用一个SEPIC配置的连接,特意减少载荷以强制实施DCM,在启动序列完成后施加一个临时步骤。在类似的工作条件下捕获并仿真一个逐周期电路。

图11 第一个SEPIC采用平均模型,第二个实施逐周期法
运行一个仿真来比较两个电路的输出响应。如图12所示,两个电路的响应非常相近。曲线的左边描述了启动序列,右边部分显示了两个模型对负载阶跃的响应。在这一阶段具有相同的响应,第一次表明平均大信号模型正确地仿真SEPIC内部,我们可进行小信号版本。

图12 平均模型与逐周期模型的瞬态响应完全符合
DCM PWM开关的大信号模型由式(10)中推导出的小信号版本所代替,与参考文献[5]中描述的不同。两个模型得出了相同的分析,但Vorpérian博士在参考文献[5]中考虑的是一个常见的配置(C端是接地的),而我们为了建立一个自动切换的DCM-CCM模型,保留了原普通无源配置。采用DCM PWM开关的小信号模型更新的电路图如图13所示。右边的参数列表计算分析所需的所有系数k。
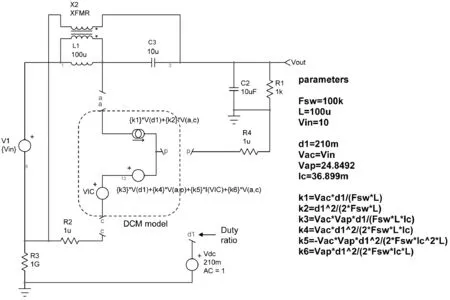
图13 这是工作在DCM模式的SEPIC的小信号模型,节点d1是占空比偏差和注入点,所有小信号系数都自动出现在参数窗口
确定准静态增益
为了确定准静态增益,需要按照图2使所有电感短路,所有电容开路。这正是SPICE在计算工作偏置点时所做的工作。然后重新排列所有的源和组件以简化电路,使其更易于分析。当您做这工作时,建议您始终运行一个全面的检查,确定新电路的动态响应与图13完美匹配。如果有任何偏差都表明您出错了,或者简化中的假设过于乐观:重复该做法直到幅值和相位完美匹配为止。组合出图14的电路。

图14 这是用来确定准静态增益H0的最终直流电路
几行代数将使我们得到输出电压表达式:
(20)

(21)
将式(20)中的Ic代入式(21)并求解Vout,得出:
(22)
该小信号准静态增益简单地表示为:
(23)
时间常数的确定
我们将采用FACTs并单独确定电路的时间常数,而不是用图13的完整原理立刻求解整个传递函数。这种方法提供了一个优势,以处理您通过对单个草图的SPICE仿真获得的结果。这大大有助于逐步前进和跟踪错误,而不至于在大量的工作时间后才发现最终的结果是错误的!
为了确定时间常数,将激励源减为0(请检查图2)。
在此,由于我们想要控制到输出的传递函数,激励源是d1。将其减为0有助于简化电路,如图15所示。

图15 将激励源减为0有助于简化电路,在此我们从驱动电感L1的阻抗开始
可以用几个公式来描述这个电路,我们知道IC= IT:
VT=V(a)-V(c)
(24)
V(a)=RloadI1
(25)
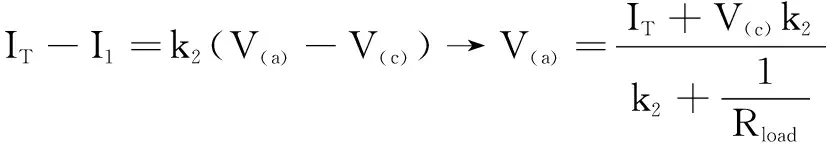
(26)
V(c)=k4V(a)+k5IC+k6V(a)-k6V(c)
(27)
将式(26)代入式(27),然后解出V(c),替代式(26)中的V(c)解得V(a),然后可写
(28)
如果您重新排列和由图13的定义替换系数k,得出时间常数τ1的定义:
(29)
二阶时间次常数指的是从C2端看到的阻抗,而L1是短路的。新的电路如图16所示。由于L1短路, a和c端在一起,简化更新的电路为右边的图片。
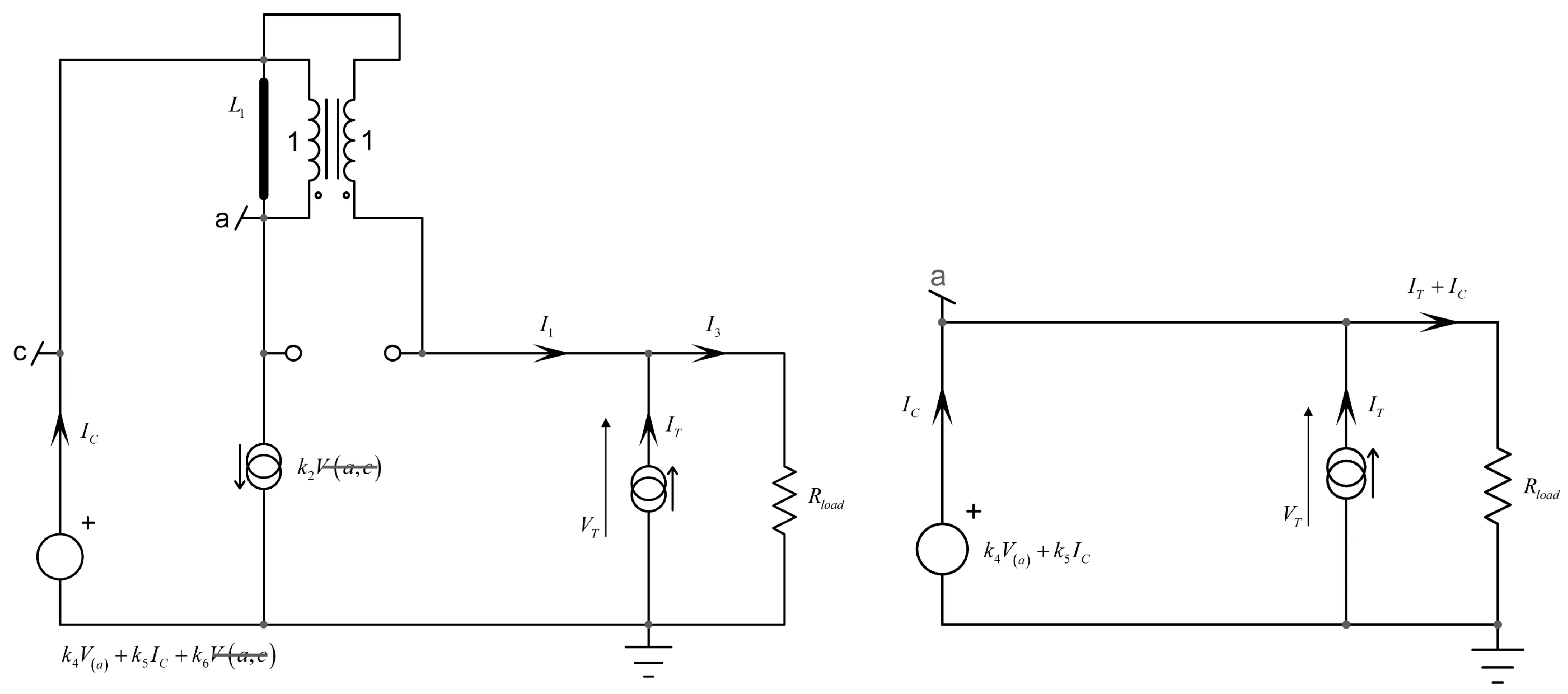
图16 使电感短路真正简化电路
再一次,几个简单的方程会很快地让您得出结果:
(31)
将式(30)代入式(31),然后解得VT并重新整理。可以发现:
(32)
如果您知道试图确定涉及C3的三阶时间常数,变压器配置(完美耦合)使其两端电压等于0 V:在动态传递函数中电容器不起作用。因此第一个系数b1定义为:
(33)
二阶系数
对于二阶系数,将设置电容C2处于其高频状态(以短路代替它),同时将确定驱动电感L1的阻抗。图17说明了这种方法。因为输出因C2短路,节点a和c都处于相同的0 V电势。电路简化为右侧示意图。
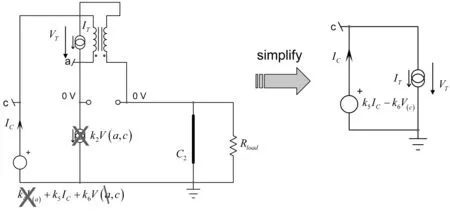
图17 二阶系数设置储能元件之一处于其高频状态(C2),同时您可确定电感两端的电阻
可写出描述VT电压的第一个方程。观察到: IT和IC是相同的,VT=-V(c),有
VT=-(k5IC-k6V(c))=-(k5IT+k6VT)→
VT(1+k6)=-k5IT
(34)
因式分解VT/IT,L1两端的阻抗为:
(35)
(36)
如果认为Vout= MVin,b2系数表示为:
(37)
合并确定的时间常数,得出分母D(s):
(38)
如果考虑一个低Q值的近似值,这二阶分母可以近似由两级联极点定义为:
(40)
和合并为:
(41)
零点的确定
如上文所述,当激励源调至零角频率sz,变形电路的响应为无信号输出(见图1)。该运用包括将激励源复原和确定无信号输出的变形电路的条件。图18所示为需要研究的更新电路。无信号输出的有趣之处在于其传播至其它节点。例如,如果Vout=0 V,然后由于变压器高边连接,节点a也处于0 V,所有涉及该节点的表达式可以简化为如图18所示。如果输出无信号,则电流I1也为0,这意味着Ic= I3。
节点c的电压定义为:
(42)
因此,电流Ic等于节点c的电压除以L1的阻抗。
(43)
而电流I3等于:
I3(s)=k1D(s)-k2V(c)=k1D(s)-k2sL1Ic(s)
(44)
现将式(43)代入式(44),然后视Ic= I3:
(45)
求解s,将系数k的值换为它们在图13中的值,重新整理,会发现
(46)

图18 在s=sz的特定条件下,观察变形的电路,无信号响应
这是个正的根源,因此为右半平面零点。通过收集所有的部分,发现极点和零点实际上是一个DCM buck-boost转换器的极点和零点,而得出完整的传递函数:
(47)
及
(50)
和
(51)
最后检查,比较Mathcad和图11大信号模型的SPICE仿真的动态响应。如图19所示,曲线完美重合。
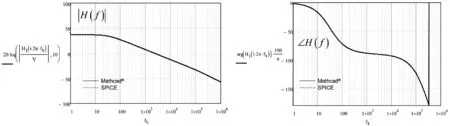
图19 Mathcad和SPICE提供完全相同的响应(曲线完美叠加)
另一个验证是由采用不同的平均模型(架构参见参考文献[11])仿真相同的SEPIC结构构建。这也是一个自动
切换的CCM-DCM模型,但走线方式稍有不同。图20所示为两种平均模型采用一个类似的SEPIC架构。

图20 CoPEC平均模型包括单独的开关和二极管连接
图21证实了两个交流响应在相位和幅值上完全相同。
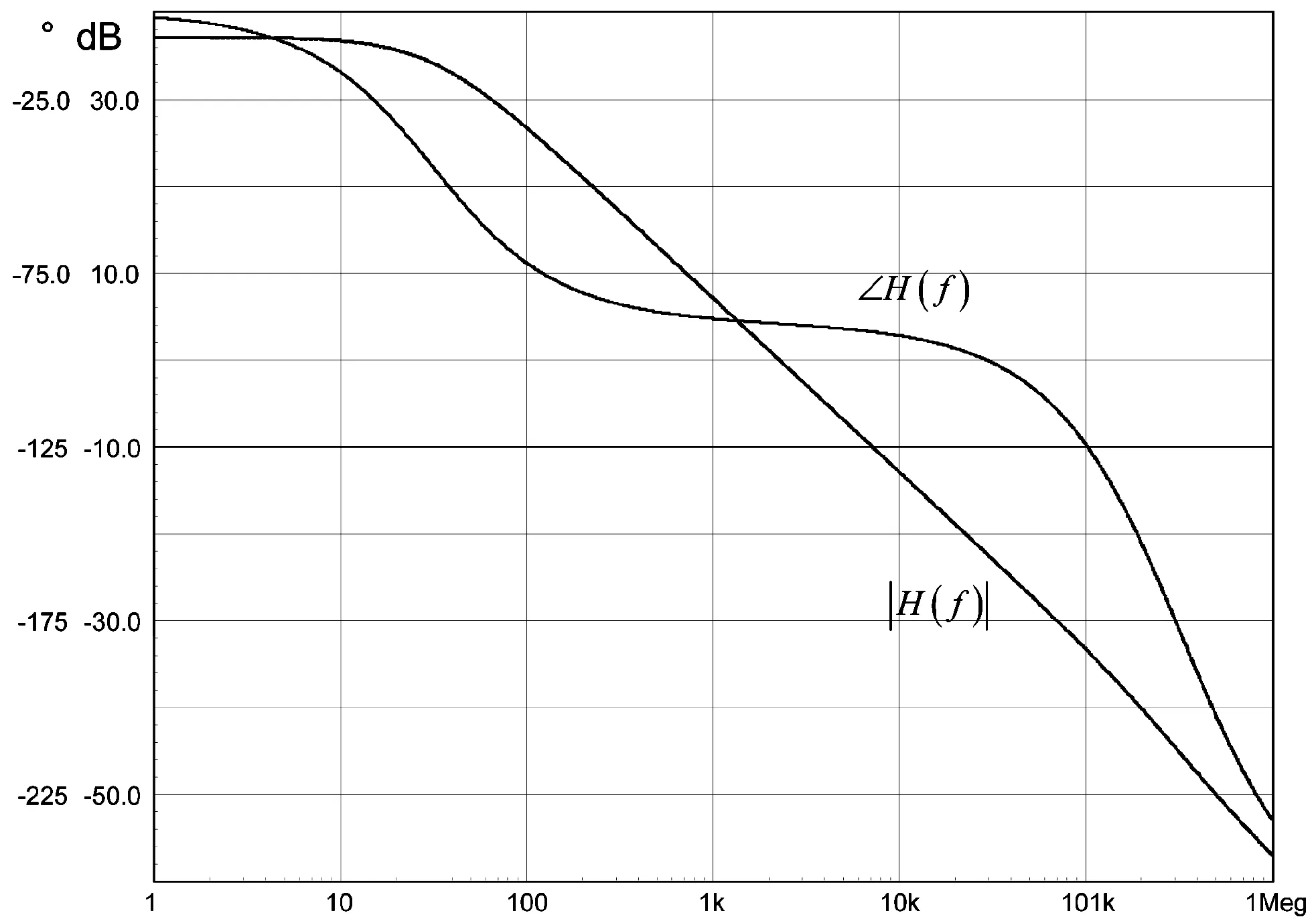
图21 DCM PWM开关和CoPEC DCM模型提供相同的动态响应
总 结

[1] R D Middlebrook.Methods of Design-Oriented Analysis:Low-Entropy Expressions,Frontiers in Education Conference,Twenty-First Annual conference,Santa-Barbara,1992.
[2] R D Middlebrook.Null Double Injection and the Extra Element Theorem[J].IEEE Transactions on Education,1989,32(3).
[3] V Vorpérian.Fast Analytical Techniques for Electrical and Electronic Circuits[M].Cambridge:Cambridge University Press,2002.
[4] C Basso.Linear Circuit Transfer Functions-An Introduction to Fast Analytical Techniques,Wiley, 2016.
[5] V Vorpérian.Simplified Analysis of PWM Converters Using the Model of the PWM Switch,Parts I and II[J].Transactions on Aerospace and Electronics Systems,1990,26(3).
[6] D Feucht.Design-Oriented Circuit Dynamics[EB/OL].[2018-02].http://www.edn.com/electronics-blogs/outside-the-box-/4404226/Design-oriented-circuit-dynamics
[7] D Peter.We Can do Better:A Proven,Intuitive,Efficient and Practical Design-Oriented Circuit Analysis Paradigm is Available,so why aren’t we using it to teach our Students? [EB/OL].[2018-03].http://www.icee.usm.edu/ICEE/conferences/asee2007/papers/1362_WE_CAN_DO_BETTER__A_PROVEN__INTUITIVE__E.pdf.
[8] C Basso.Fast Analytical Techniques at Work with Small-Signal Modeling[EB/OL].[2018-03].http://cbasso.pagesperso-orange.fr/Spice.htm.
[9] J Betten.Benefits of a coupled-inductor SEPIC,slyt411,application note,Texas-Instruments.
[10] C Basso.Switch-Mode Power Supplies:SPICE Simulation and Practical Designs,McGraw-Hill, 2nd edition,2014.
[11] D Maksimovic,R Erickson.Advances in Averaged Switch Modeling and Simulation,Power Electronic Specialist Conference Professional Seminar,Charleston,1999.
