方板阶梯辐射体指向性研究

李娜，贺西平，武婷婷



方板阶梯辐射体指向性研究

李娜，贺西平，武婷婷

(陕西师范大学物理学与信息技术学院，陕西省超声学重点实验室，陕西西安 710119)

指向性是衡量辐射体声学性能的重要参数。同相弯曲振动方板阶梯辐射体具有辐射阻抗低、面积大等特点，可广泛应用于大功率气介质超声领域。分别从材料、几何尺寸两个方面对影响辐射体指向性的因素进行了研究。并以材料为钢，边长为50 mm，基底厚度为6 mm，阶梯厚度为10 mm的方板阶梯辐射体(II#)为例，利用有限元将辐射体划分为多个微元，提取各微元位移振幅，计算其指向性。计算结果表明，工作频率一定时，材料对辐射体的指向性没有影响；当辐射体边长与基底厚度的比值较小时，其指向性较尖锐。实验测试与理论计算结果相符，方板阶梯辐射体指向性图案有单一主瓣，其辐射主要集中在主轴方向，形成一个半开角宽度较小的锥形射线束。

方板阶梯辐射体；指向性；材料；几何尺寸

0 前言

声辐射的空间分布具有方向性，即在某些方向辐射很强，而在其他方向较弱，为了描述声源辐射随方向而异的特性，定义了指向性这一物理量，它是描述辐射体声学性能的重要参数[1]。例如，文献[2]介绍了全保偏光纤水听器的基元结构和工作原理，描述了四基元阵列结构和性能，给出了光纤水听器基元相对接收灵敏度的频率响应和阵列指向性的测量结果。文献[3]针对同时存在着自由液面和刚性壁面的复杂声边界问题，结合镜像法原理，应用双反射方法推导了复杂声边界条件下圆柱壳结构的远场声压方程式。最后，以直角空间域内的圆柱壳结构为例，对结构的声振特性进行了数值计算。在算例中，对比了声边界特性、频率及与声边界的距离对声辐射功率、声辐射指向性的影响。文献[4]利用边界元方法，在不规则障板边界条件下,对矢量传感器的散射声场进行了计算，得出了矢量传感器的指向性图案。

在由压电纵振换能器和弯曲振动辐射体(薄圆盘或薄板)组成的超声波辐射系统中，压电纵振换能器激励辐射体做弯曲振动。纵振换能器具有高效率、大功率等特点，弯曲振动辐射体具有低辐射阻抗、大面积等特点，由此该辐射系统在大功率气介质超声领域获得了广泛运用。常用辐射体一般为圆形、矩形[5-10]。文献[11]对平圆盘的指向性进行了测试，结果表明其指向性不尖锐。这是由于圆盘表面节线两侧振动相位相反，产生相消干涉。为减小相消干涉，可以选择具有圆形节线的振型作为工作振型[12-13]，在振动相位相反区域加阶梯(厚度为辐射体在辐射介质中对应声波波长的一半)，可将其改进为同相弯曲振动阶梯圆盘，实验测试表明，阶梯圆盘指向性尖锐。文献[14]和文献[15]以自由边界阶梯圆盘为例，提出了阶梯圆盘频率方程的解算方法，计算了阶梯圆盘的指向性。矩形平板具有节线与其长边(或宽边)平行的条纹振型[16]。文献[17]利用导纳法对矩形平板辐射体的指向性进行了研究。文献[18]对矩形平板辐射体及由其改进得到的矩形阶梯板辐射体的指向性进行了计算与测试。

本文利用纵向振动换能器激励方形平板辐射体，纵向振动换能器频率与方形平板辐射体第四阶本征振动频率相同，该频率在超声常用频率范围内，得到具有直节线的响应振型，选择该振型作为工作振型，可较方便地将方形平板辐射体改进为同相弯曲振动阶梯辐射体。与线性尺寸相同的矩形阶梯辐射体、圆盘阶梯辐射体相比，方板阶梯辐射体频率明显偏低，这个特点决定了其在空气中辐射时传播距离较远，在测距、料位测量、超声清洗、除泡、干燥等领域具有非常好的应用前景。

1 方形辐射体振型计算

以边长50 mm，基底厚度6 mm的方形平板辐射体(I#)为例，材料为45#钢，泊松比=0.28，杨氏模量=1.96×1011 N.m-2，密度=7.91×103kg.m-3。通过有限元法计算得到该方形平板辐射体的第四阶本征振型对应的频率为19 332 Hz。

如图1(a)所示，用频率为19 332 Hz的纵向振动换能器激励方形平板辐射体中心，有限元Model模块计算得到如图1(b)所示的响应振型。该响应振型在方板本征振型中不存在[19-20]，只有纵振激励方板时才出现，此时系统谐振频率为19 006 Hz。计算方形平板辐射体沿边长方向的振动位移，从而确定方形平板辐射体沿边长方向的八个节点的位置坐标，节点编号见图1(b)上的标示。分别连接节点1与节点8、节点2与节点3、节点4与节点5、节点6与节点7，即可确定辐射体的四条节线。以节线与板角围成的直角三角形区域为阶梯区域，在该区域加阶梯，可将平板辐射体改进为阶梯辐射体(II#)，阶梯辐射体在阶梯高度所在平面产生了同相弯曲振动，从而避免了相消干涉。换能器在原频率激励上加了阶梯的方板辐射体，节线会外扩。重新计算节点位置、阶梯区域及阶梯厚度，直到阶梯边缘与节线位置相重合。最终确定阶梯厚度为1/2(340/2×15 751) m0.01 m(见图1(c))，为声波在空气中的传播速度，方板阶梯辐射体振动频率15 751 Hz。

2 辐射体的指向性

2.1 计 算

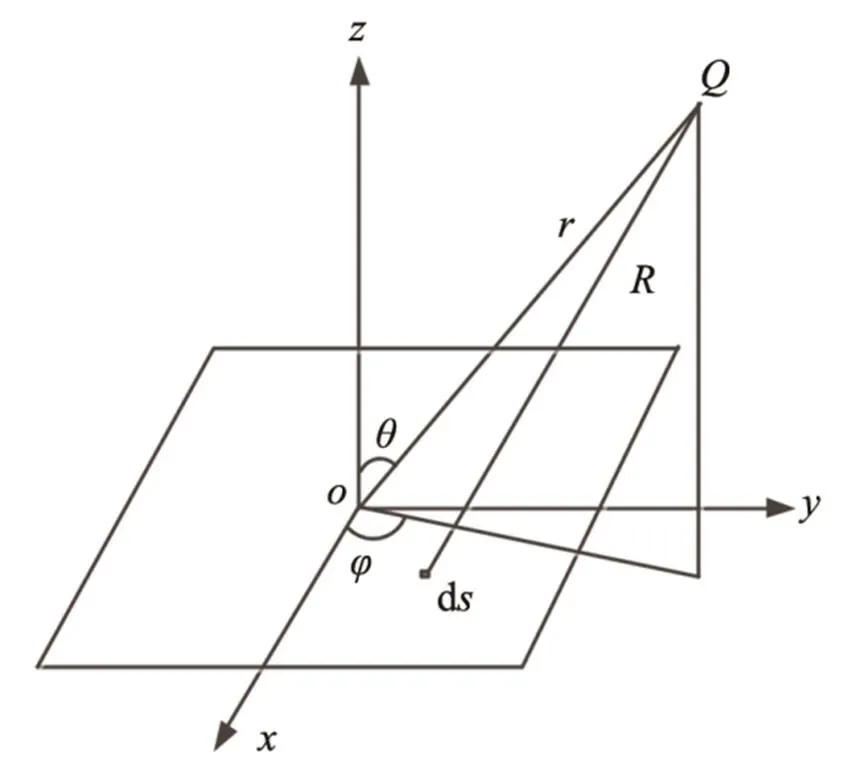
图2 辐射声场计算示意图

由离散瑞利积分公式，根据指向性定义，可得方板辐射体辐射声场指向性为[18]

选择单元类型为SOLID187，方板阶梯辐射体的单元数量为709个，利用有限元Modal模块，计算可得到各单元的振动位移，提取板平面上单元的位移，结合式(1)和式(2)，可得方板阶梯辐射体的指向性。

2.2 影响因素

指向性是辐射体声学性能的重要参数，本文将分别从材料、几何尺寸两个方面对影响方板阶梯辐射体指向性的因素进行研究。

2.2.1 材 料

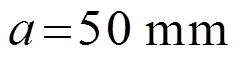
表 1 四个尺寸相同辐射体的不同材料参数

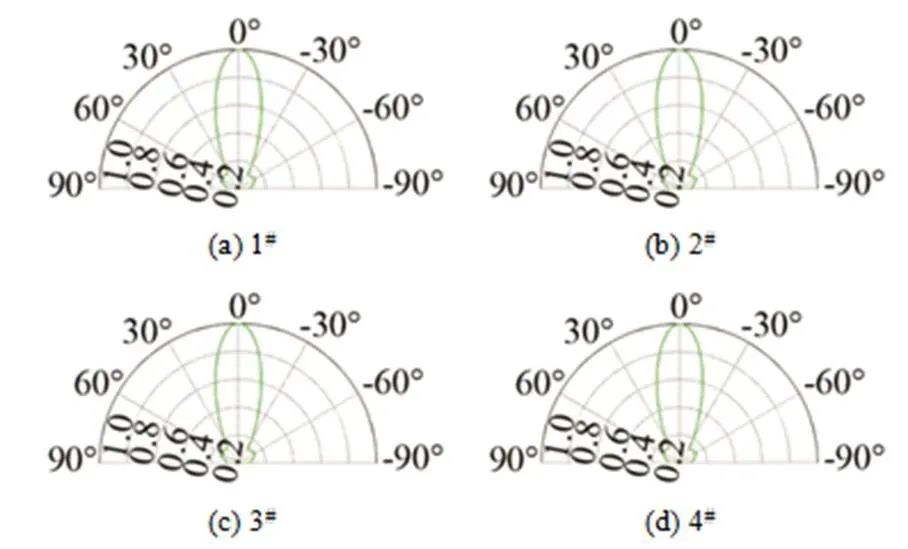
图3 表1中四个方板阶梯辐射体在φ=90°平面内的指向性

2.2.2 几何尺寸

方板阶梯辐射体(材料为钢)具有相同的频率，对应的边长基底厚度及阶梯厚度1如表2所示，计算得到的指向性图案如图4所示。

表 2 四个频率相同钢辐射体的几何参数

图4 表2中四个方板阶梯辐射体在φ=90°平面内的指向性

方板阶梯辐射体(材料为钢)具有相同基底厚度，对应边长阶梯厚度1及频率如表3所示，计算得到的指向性图案如图5所示。

表3 四个基底厚度相同钢辐射体的几何参数

图5 表3中四个方板阶梯辐射体在φ=90°平面内的指向性

方板阶梯辐射体(材料为钢)具有相同边长，对应基底厚度、频率及阶梯厚度1如表4所示，计算得到的指向性图案如图6所示。

表4 四个基底边长相同钢辐射体的几何参数

图6 表4中四个方板阶梯辐射体在φ=90°平面内的指向性

3 实验

加工方板阶梯辐射体(II#)，如图7所示，测试其指向性。超声波发生器施加频率15 751 Hz的激励信号于换能器，换能器中心激励方板阶梯辐射体，辐射体中心正对uc-29麦克风(日本里音公司产，1/4 in(1 in=25.4 mm)，频响范围为20 Hz～100 kHz)，每5°转动辐射体一次，每转一次接收到的信号经过前置放大器放大后导入声级测量分析仪中(型号为NA-42，日本里音公司产，频响范围为1 Hz～100 kHz)，即可测试得到一次声级值，将各测点的声级值换算为声压值后，编程计算可得到辐射体的声场指向性，如图8虚线所示。

图7 加工好的方板阶梯辐射体

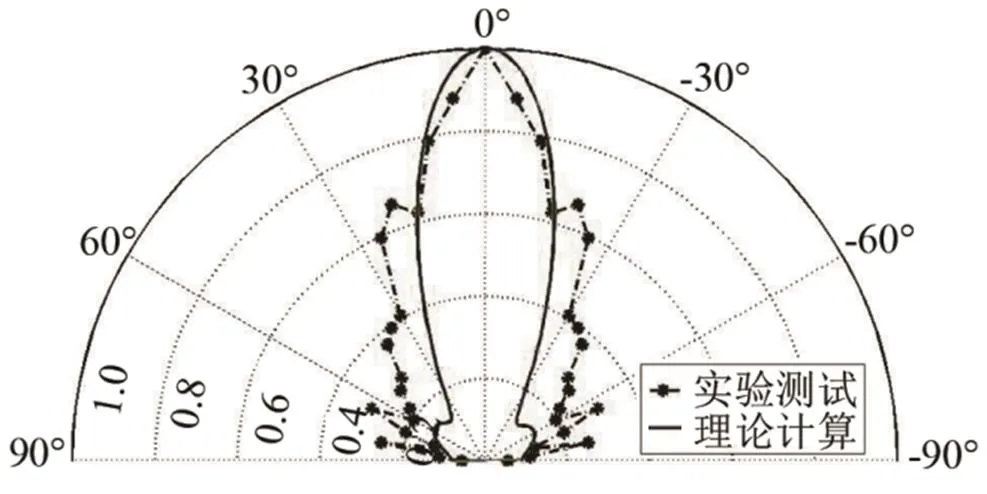
图8 计算和测量的辐射体在φ=90o平面内的指向性

4 分析与讨论

4.1 实验与计算

计算与测试得到的方板阶梯辐射体的指向性图案轮廓基本一致，两者均具有单一主瓣，辐射主要集中在主轴方向，形成一个锥形射线束，其半开角宽度较小，指向性尖锐。但还是存有一些差异，主要表现为测试得到的指向性主瓣较宽。可能原因是，理论计算时假设辐射体嵌置于无限大刚性障板中，而测试时辐射体实际嵌置于有限大障板中；再者，辐射体阶梯边缘会产生衍射，但衍射声场的影响不会很大；其次，计算所用的材料的杨氏模量等值是取自材料的标准值，可能与实际有差别；最后，辐射体机械加工及装配过程有一定误差。

4.2 指向性影响因素

由图3可知，钢、铝、镍、铜四种不同材料、相同频率的方板阶梯辐射体的指向性图案基本一致，这说明在工作频率一定时，材料对辐射体的指向性没有影响。

具有相同频率、不同几何尺寸的方板阶梯辐射体，当边长与厚度的比值逐渐减小时，辐射体指向性逐渐尖锐，如图4所示。进一步计算方板阶梯辐射体指向性与其几何尺寸的关系，结果表明当方板阶梯辐射体的基底厚度相同时，逐渐减小边长(即边长与基底厚度的比值减小)，辐射体指向性逐渐尖锐，如图5所示。当方板阶梯辐射体的边长相同，逐渐增大其基底厚度，如图6所示，指向性逐渐尖锐。以上计算结果均说明，方板阶梯辐射体边长与基底厚度的比值较小时，对应辐射体的指向性尖锐。

5 结论

本文计算了方板阶梯辐射体的指向性。从材料、几何尺寸两个方面对影响辐射体指向性的影响因素进行研究，得到如下结论：

(1) 方板阶梯辐射体具有尖锐的指向性。计算与测试得到的方板阶梯辐射体的指向性图案轮廓基本一致，两者均具有单一主瓣，辐射主要集中在主轴方向，形成一个锥形射线束，其半开角宽度较小；

(2) 工作频率一定时，材料对辐射体的指向性没有影响；

(3) 具有相同频率、不同几何尺寸的方板阶梯辐射体，当边长与厚度的比值逐渐减小时，其指向性变尖锐；

(4) 具有相同基底厚度的方板阶梯辐射体，当边长逐渐减小时，对应辐射体的频率逐渐增大，辐射体指向性变尖锐；

(5) 具有相同边长的方板阶梯辐射体，当基底厚度逐渐增大时，对应辐射体的频率逐渐增大，辐射体指向性变尖锐。

[1] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2012. DU Gonghuan, ZHU Zhemin, GONG Xiufen. The Foundations of Acoustics[M]. Nanjing: Nanjing University Press, 2012.

[2] 孟洲, 胡永明, 熊水东. 全保偏光纤水听器阵列[J]. 中国激光, 2002, 29(5): 415-417. MENG Zhou, HU Yongming, XIONG Shuidong. All polarization maintaining fiber hydrophone array[J]. Chinese Journal of Lasers, 2002, 29(5): 415-417.

[3] 王威, 陈炉云. 含复杂声边界的圆柱壳结构声振特性研究[J]. 振动工程学报, 2016, 29(6): 1034-1040. WANG Wei, CHEN Luyun. Vibro-acoustic characteristics of cylindrical shells with complex acoustic boundary conditions[J]. Journal of Vibration Engineering, 2016, 29(6): 1034-1040.

[4] 陈亚林, 杨博, 马远良. 复杂边界条件下矢量传感器的指向性分析及实验研究[J]. 声学技术, 2006, 25(4): 381-386. CHEN Yalin, YANG Bo, MA Yuanliang. Analysis and experiment study on directivity of vector sensor located on complicated boundaries[J]. Technical Acoustics, 2006, 25(4): 381-386.

[5] BARONE A, GALLEGO J A. Flexural vibrating free-edge plates with stepped thicknesses for generating high directional ultrasonic radiation[J]. J. Acoust. Soc. Am., 2005, 51(3): 953-959.

[6] GALLEGO J A, RIERA E, ACOSTA V. Ultrasonic system for continuous washing of textiles in liquid layers[J]. Ultrasonics Sonochemistry, 2010, 17(1): 234-238.

[7] GONZALEA I, RODRIGUEZ J, GARMENDIA I. Application of high intensity air-borne ultrasound for debubbling liquid coating layers[J]. Ultrasonics, 2006, 44(1): 529-532.

[8] RODRIGUEZ G, RIERA E, GALLEGO J A. Experimental study of defoaming by air-borne power ultrasonic technology[J]. Physics Procedia, 2010, 3(1): 135-139.

[9] GALLEGO J A, RODRIGUEZ G, GALVEZ J C, et al. A New High-intensity ultrasonic technology for food dehydration [J]. Drying Technology, 1999, 17(3): 597-608.

[10] JAMBRAK A R, MASON T J, PANIWNYK L. Accelerated drying of mushrooms, Brussels sprouts and cauliflower by applying power ultrasound and its rehydration properties[J]. Journal of Food Engineering, 2007, 81(1): 88-97.

[11] OTSUKA T, KAMISHIMA Y, SEYA K. Aerial ultrasound source by stepped circular vibrating plate[J]. Japanese Journal of Applied Physics, 1983, 22(S3): 108.

[12] 贺西平, 宋旭霞, 李伟. 阶梯圆盘的设计及其声参数计算[J]. 声学学报, 2010, 35(5): 502-507. HE Xiping, SONG Xuxia, LI Wei. Design flexural vibrating stepped thin plate and calculating its acoustic performances[J]. Acta Acustica, 2010, 35(5): 502-507.

[13] MARY D W. Vibrations of free circular plates: part I. Normal modes[J]. Proceedings of the Physical Society, 1938, 50(1): 70-76.

[14] MARY D W. Vibrations of free circular plates: part II. Compounded normal modes[J]. Proceedings of the Physical Society, 1938, 50(1): 77-82.

[15] HE X P, YAN X L, LI N. Directivity pattern of the sound radiated from axisymmetric stepped plates[J]. J. Acoust. Soc. Am., 2016, 140(2): 1387-1396.

[16] MARY D W. Vibrations of free rectangular plates[J]. Proceedings of the Physical Society, 1949, 62(5): 277-285.

[17] BUDARAPU P R, NARAYANA T S, RAMMOHAN B. Directionality of sound radiation from rectangular panels[J]. Applied Acoustics, 2015, 89: 128-140.

[18] LI N, HE X P, Yan X L. Investigation of directivity patterns of the sound radiated from circular and rectangular plates[C]//IEEE Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), 2016: 395-398.

[19] MARY D W. Vibrations of free square plates: part I. Normal vibrating modes[J]. Proceedings of the Physical Society, 1939, 51(5): 831-844.

[20] MARY D W. Vibrations of free square plates: part II. Compounded normal modes[J]. Proceedings of the Physical Society, 1940, 52(4): 452-455.

Research on the directivity of square plate stepped radiator

LI Na, HE Xi-ping, WU Ting-ting

(School of Physics and Information Technology, Shaanxi Normal University, Shaanxi Key Laboratory of Ultrasonics, Xi’an 710119,Shaanxi, China)

The directivity is an important parameter for evaluating radiator. With the features of low impedance and large surface, the square plate stepped radiator in bending vibration has been widely applied in high power air ultrasonic processing. For an example of square steel plate stepped radiator, the side length and thickness of the base plate are 50 mm and 6 mm respectively, and the stepped thickness is 10 mm. By using finite element method, the directivity pattern of the radiator is calculated. It shows that the square plate stepped radiator exhibits better directivity, for its major lobe is sharper and its side lobes are small. In addition, the relationships of both material and geometrical dimension with directivity pattern are studied. It shows that the directivity of the square plate stepped radiator is independent of material but dependent on radiator dimensions. The smaller of the side length to thickness ratio of the radiator, the shaper of the directivity pattern will be. Finally, the directivity of a fabricated radiator is measured, and it shows that the calculated result is in good agreement with the measured one.

square stepped radiator; directivity; material; geometrical dimension

O426.1

A

1000-3630(2018)-01-0006-05

10.16300/j.cnki.1000-3630.2018.01.002

2017-09-09;

2018-01-17

国家自然科学基金资助项目(11774211)

李娜(1984－), 女, 宁夏西吉人, 博士研究生, 研究方向为功率超声。

贺西平, E-mail: Hexiping@snnu.edu.cn