改进型遗传算法在环境噪声反演海底问题中的应用
2018-04-11陈勃赵梅胡长青
陈勃,赵梅,胡长青
改进型遗传算法在环境噪声反演海底问题中的应用
陈勃1,2,赵梅2,胡长青2
(1. 中国科学院大学,北京 100049; 2.中国科学院声学研究所东海研究站,上海 201815)
利用浅海环境噪声进行海底特性反演一直是学者们研究的热门课题之一,当考虑两层海底时,由于待反演参数较多,基于传统遗传算法的反演策略往往使反演过程陷入局部最小值,从而无法找到全局最优解。针对两层海底的情况,计算得到了浅海环境噪声场空间相干性的表达式,并对传统遗传算法进行了改进,通过引进自适应交叉和变异算子以及能够保持种群多样性的小生境技术来提高反演算法的性能。通过数值仿真,验证了改进后的算法较传统算法能更好地收敛到真实值;并针对一次海试数据进行了海底特性反演,获得了较好的结果。
遗传算法;小生境;浅海噪声场;海底反演
0 引言
环境噪声作为海洋中的背景声场,存在于任何海洋环境中。噪声在传播过程中不断与海底发生接触,携带有海底信息,这使得利用环境噪声反演海底特性成为了可能。这种方法较传统的主动探测方法,具有成本低、隐蔽性好和探测设备简单等优势,因此成为了人们研究的热门课题之一[1-7]。
在反演过程中最常采用的算法是遗传算法[8-10]。遗传算法(Genetic Algorithm,GA)是达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过自然进化过程搜索最优解的方法。遗传算法最早由John Holland[11]提出,并引进了群体、适应度、选择、变异、杂交等基本概念。1975,年Holland[11]发行了一本遗传算法方面的著作,该著作对遗传算法的基本理论以及人工自适应系统做了详细的论述。1989年,Goldberg[12]首次将遗传算法运用在实际的工程系统优化问题当中。遗传算法具有很强的全局搜索能力,通用性强,鲁棒性高,因而被广泛地应用于很多领域。
但是,遗传算法随着进化过程的不断延续,会造成群体模式的种类逐渐趋于单一,使得群体内部近亲繁殖,选择、交叉算子失去了应有的作用,令算法难以跳出局部最优解。在海底反演的问题中,通常我们考虑包含沉积层和基底的双层海底模型,每一层海底都至少考虑声速、密度和衰减系数这三个主要参数,再加上沉积层的厚度,那么代价函数中包含的参数至少为7个,这会使得代价函数有多个局部最优解,运用遗传算法反演时会更容易早熟、陷入局部极值中。本文提出了一种改进的遗传算法,将小生境技术[13-16]应用在算法中,以保证种群的多样性,并引入一种自适应的交叉和变异算子,提高了算法性能。仿真结果显示,改进后的遗传算法能够使代价函数更好地收敛到全局最优解,随后将该算法运用到实验数据中,反演结果经验证该算法是可靠的。
1 浅海环境噪声场理论模型
本节讨论的是浅海海洋环境下,风成海面噪声源噪声场的垂直相关性。与深海相比,浅海环境比较简单,可以不必考虑深海声道轴或海底山对于声传播的影响。噪声在浅海这一声信道中传播时不断地在海底海面处发生反射,因此界面的特性决定了浅海噪声场的空间结构。另外,当声波频率较低时,其波长将远大于海面的不平整程度,这时粗糙海面对于噪声的散射效应可以忽略不计,海面被简单地视为一个压力释放界面。综合以上考虑,在浅海环境中海底特性是决定噪声场空间相关性的最重要因素。
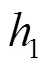
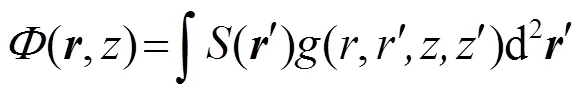
其中:S为噪声源谱强度,为格林函数,噪声场的空间相干性用(,)点声场和(,)点声场的互谱密度值表示,这一互谱密度写为,互谱密度代表了噪声场的空间特性,这一特性可以通过不同水听器间接收到信号的相干表示出来,若两点的位置重合,则该互谱密度转化为噪声场在该点的声强度。互谱密度写为以下形式:

另有:

将式(1)和式(3)代入式(2)化简后,得


将噪声源分为两部分:距离接收点较近的近场声源和距离接收点较远的远场声源,近场和远场的计算分别采用射线和简正波的方法[17],式(4)写为

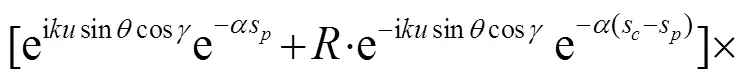

式(6)中,表示界面反射系数;是近场与远场的分界点;为掠射角;为两接收点连线的俯仰角;为两接收点之间的距离;代表一个完整的声循环距离;代表最后一个海面反射点到接收器的距离。在大于距离的远场,噪声场空间相关函数通过模态函数的形式表示为

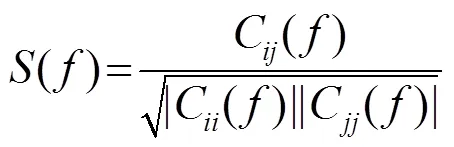
另外,由于风关噪声本身是一个频率从102~103(Hz)量级变化的宽带声源,因此在计算的时候将其表示为频域的形式,即将各窄带计算结果合成,以频域相干的形式来表示噪声场空间特性。归一化功率谱密度也将作为反演物理量在接下来的反演过程中使用。
2 改进遗传算法仿真研究
2.1 改进策略
遗传算法由生物进化理论发展而来,通过模拟生物种群中个体的杂交、变异及选择过程来实现优化种群、筛选最优子代的目的。由于遗传算法的进化特性,在搜索过程中不需要对其适应度函数有特殊限制,无论是离散还是连续、可微还是不可微、线性还是非线性的函数,均可作为其适应度函数,而且遗传算法所要处理的对象较容易编码,进化过程也容易通过计算机编程实现,因此其在解决一些优化问题时体现出了很大的优势。但是面对一些多维的、存在很多局部极值点的问题,传统的遗传算法往往存在早熟收敛、搜索性能不高、易陷入局部最优解的问题。其主要原因是随着进化代数的增加,种群的多样性慢慢降低,遗传算法的交叉算子和变异算子的作用减弱,这样在种群中就很难再出现适应度更大的某个个体了,算法也就会陷入局部最优解而很难跳出。噪声场反演问题便属于这一类多维且存在众多局部最优解的问题,如第1节中采用的双层海底模型,其参数为7个,传统的遗传算法很难收敛到真实值,因此,在本节中,作者提出了一种改进的遗传算法,通过自适应交叉和变异算子,以及能够保持种群多样性的小生境技术来提高算法的性能。
2.1.1 自适应交叉和变异算子
就一未知海域来说,在先验知识有限的情况下,参数的范围必须设置得足够大才能保证算法在运算的过程中可以尽量遍历到所有可能值,例如声速的变化范围,在不同的底质中会从1 500 m.s-1(粘土)变化到5 000 m.s-1(玄武岩),这样大的变化区间,在进化初期,为了增强群体的多样化程度,使子代个体在整个先验空间中分布,加大个体之间的竞争,就必须扩大父代个体之间的杂交和变异操作。但是随着进化次数的增加,子代逐渐向最优解靠近,这时如果再使用比较大的杂交率,会产生许多发散分布在整个搜索空间的新的个体,会稀释原本适应度较好的种群;同样这时如果变异率还保持在比较高的值,则会使父代中的一些优良基因丢失,也会稀释本来适应度较高的种群。于是,在本文中使用了一种自适应的交叉和变异算子,基本的思想是在进化前期使用较高的交叉和变异率,而随着进化代数的增加,根据种群适应度的变化逐渐降低交叉和变异率。使用公式表示为如下形式:


2.1.2 小生境技术
小生境是生物学中的一个概念。生物在其进化过程中一般总是与自己相同的物种生活在一起,共同繁衍后代,因此在每一个小生境内,基因的多样性会慢慢下降,反映到遗传计算中则是子代容易聚集在某一小生境中,杂交和变异算子慢慢失效。为了克服这一弊端,在进化计算中,将每一代个体划分为若干类,每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群,再在种群中或不同种群之间杂交、变异产生新一代个体。这种由生物学概念发展来的技术即称为小生境技术,我们将它运用在噪声反演海底的工作中,以避免反演过程的早熟现象。
首先在产生新一代的个个体后,用海明距离来表示这个个体之间的差异,从而将子代划分为不同的小生境,海明距离的计算方法由式(11)表示:
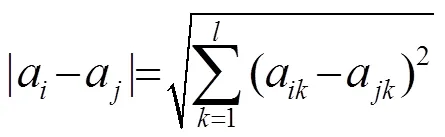


经过改进后的遗传算法流程图如图2所示。
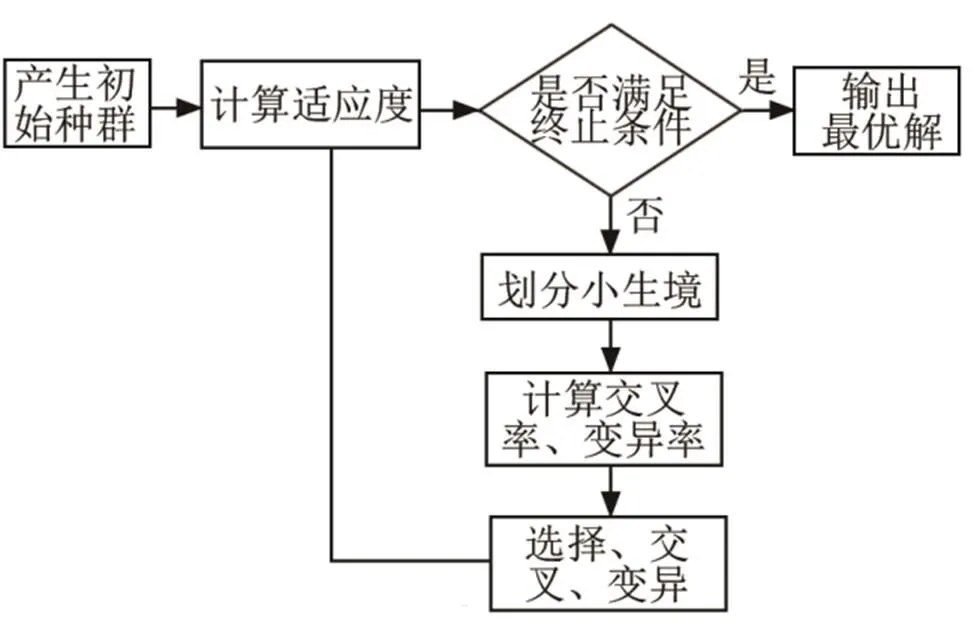
图2 改进遗传算法流程图
2.2 与传统遗传算法仿真结果对比
在2.1节中确定了遗传算法的改进思路:分别通过小生境技术和动态算子来保证种群的多样性与收敛效果。为了验证改进后算法的性能,在本节中利用第1节中的正演模型得到浅海噪声场的垂直相干系数,再分别利用基于传统遗传算法和改进遗传算法的反演模型进行海底声学参数的反演,比较反演结果。算法采用的代价函数由式(13)表示,该代价函数也作为算法中的适应度函数:
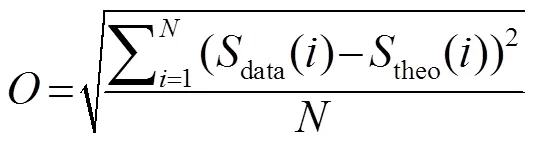
正演模型采用图1所示的海洋环境,海水深40 m,海水中的声速和密度分别为1 500 m.s-1和1.0 g.cm-3;海底视为一双层海底,即包括沉积层和基底,沉积层的厚度为5 m,沉积层中的声速为1 750 m.s-1,密度为1.5 g.cm-3,衰减系数为0.2 dB.l-1;基地为半无限大空间,声速为3 000 m.s-1,密度为2.5 g.cm-3,衰减系数为0.1 dB.l-1。
反演参数设置如下,种群规模为100,待反演参数为7个,分别为沉积层厚度2、沉积层声速2、沉积层密度2、沉积层衰减系数2、基底声速3、基底密度3、和基底衰减系数3。采用二进制编码形式,参数初始值范围设置如表1所示。

表1 海底参数初始值范围
图3和图4为传统遗传算法和改进后遗传算法的适应度值对比。图3为每一代种群最小适应度值的变化情况,由此可以看到,对于传统遗传算法,代价函数在20代时收敛到局部最小值,不能跳出;而对于改进的遗传算法,代价函数在20代时已达到0.1%,且在20代之后依然逐渐减小,向全局最优解靠拢。图4为每一代种群平均适应度值的变化情况,传统遗传算法在20代开始,均值在0.01上下波动,无法继续收敛,因为此时传统遗传算法陷入了局部极值,由于早熟而无法继续寻找全局最优解,这与图3反映的情况吻合,改进的遗传算法由于保证了种群的多样性,在反演的过程中未陷入局部极值,而是逐渐向全局最优解靠拢。
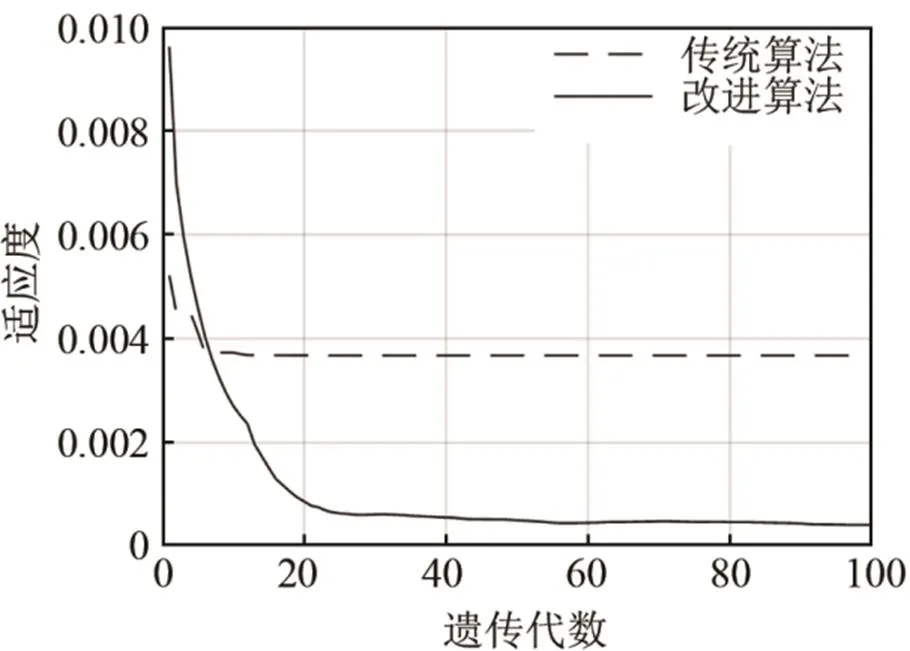
图3 改进型遗传算法和传统遗传算法最小适应度值对比

图4 改进型遗传算法和传统遗传算法平均适应度值对比
计算终止的判定条件设置为:进化到100代时终止。表2记录了100代时改进型遗传算法和传统遗传算法的结果比较。使用传统的遗传算法时反演模型和理论模型误差很大,而使用基于动态算子和小生境技术的改进遗传算法,其反演结果效果得到大幅度提高,获得了精度更高的解。究其原因还是在于传统算法早熟的问题,在表1所设置的搜索空间中,存在很多个局部极值点,传统算法计算时一旦陷入某个局部极值区域,便无法跳出,此时得到的结果与真实值还有较大差距。

表2 改进型遗传算法与传统遗传算法反演结果比较
通过表2可以看到,无论是改进算法还是传统算法,沉积层声速均能很好地收敛到真实值,即使误差较大的传统算法,反演结果的误差也只有2.61%,远远好于其它参数。因为沉积层的声速在噪声场模型中对于相干计算结果有着重要影响,垂直相干系数对于沉积层的声速也最为敏感。而对于基底的密度,改进后的遗传算法反演结果依然与理论模型存在9.27%的误差,说明模型对于基底密度的敏感性最低,反演也最困难。
3 实验及结果分析
3.1 改进策略
通过第2节的仿真研究,验证了改进后的遗传算法较传统方法拥有更好的性能,在本节中利用实验数据进行海底声学参数的反演。实验数据来自于一次某海域夏季浅海环境噪声实验。实验利用一潜标采集了连续若干小时内的环境噪声,本次实验采用的接收器工作频带为20 Hz~20 kHz,内置20 dB前置放大器。在实验进行的前、中、后期,工作人员利用温盐深仪(Conductance Temperature Depth,CTD)对海水温深剖面均进行了测量,图5是声速剖面测量的平均值。从图5可以看到声速剖面的特征是,在上层约20 m内为等温混合层,具有等声速结构,20~35 m深度内为温跃层。实验所用测量水听器位于温跃层以下,因此接收处掠射角认为与海底处掠射角相等,而与海面噪声源处出射角之间的关系满足斯奈尔定律:
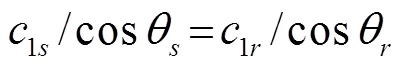
实验利用水听器阵列对浅海环境噪声进行连续接收,该实验在禁渔期进行,且远离航道,因此可忽略航船噪声的干扰。实验期间海面风力为8~10 m.s-1,具备良好的风成噪声条件。
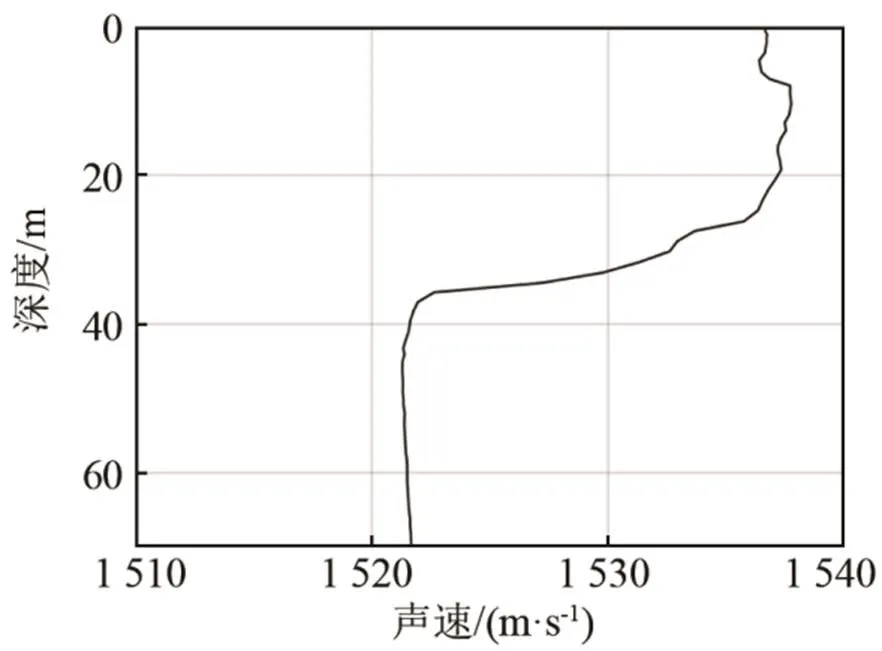
图5 实验海域声速剖面
3.2 反演结果及分析
反演所用物理量为噪声场的频域相干曲线,为了得到该值,首先对采集到的噪声数据进行分段,对每一段数据进行滤波及傅里叶变换,然后取这若干段数据傅里叶变换后的平均值,即得到实验数据的频域相干曲线。反演时分别采用传统遗传算法和改进后的遗传算法进行对比,结果通过均方误差衡量,其公式为

反演结果通过相对均方误差进行衡量,图6是改进后遗传算法与传统遗传算法相对均方误差的对比,使用传统遗传算法进行优化,均方误差在20代左右基本稳定,保持在5%~6%之间;而改进型遗传算法,其均方误差一直朝最小值靠近。设定终止条件为均方误差小于0.1%,改进后的算法在80代时已达到最优解。从图6中可以看到,改进后的遗传算法能够有效改善传统算法易于陷入局部收敛的缺陷,这与第2节仿真中得到的结论相吻合。

图6 反演结果相对均方误差对比
对反演结果的后验概率密度分析是一种较为常用的反演结果分析手段,在未得到直接采样的海底底质情况下,可以有效地对反演结果进行分析和验证。本文假设各参数在先验空间中满足均匀分布,以遗传算法中的适应度函数作为似然函数,计算得到8个待反演参数的后验概率密度(Posterior Probability Density,PPD)如图7所示。


实验时,三个温深仪分别固定在水听器阵列的上、中、下三个位置处。根据其记录的深度数据,以及阵列本身的长度,可以得到在数据获取时间段内,阵列的倾斜角度为41°左右,与反演结果吻合较好。另外,实验海域沉积层的声学参数在文献[18]中有记录,该海域表层沉积物为粉质细沙,其平均颗粒度约为4,对应的沉积层声速和密度分别在1 680 m.s-1和1.76 g.cm-3左右,与反演得到的结果吻合较好。

表3 实验数据反演结果

图8 反演相干系数和实验值的对比
4 结论
利用环境噪声反演浅海海底特性,可以大幅简化实验设备,有效提高反演效率,节约成本。传统的反演策略以遗传算法和模拟退火算法为主。但当待反演参数较多时,传统算法易出现早熟,陷入局部最优解而无法跳出。本文针对这一问题,对传统算法进行了改进,引入了自适应的交叉和变异算子,保证算法在前期能够加快搜索速度,而在后期可以根据收敛情况调整降低交叉及变异概率,从而加快收敛速度;同时引进了小生境的思想,以保持种群多样性,防止算法早熟。针对改进后的算法,文中第2节中利用仿真验证了其性能,改进后的算法较传统算法收敛情况有明显的改进,能够较好地收敛到全局最优解。最后利用海洋环境噪声数据进行了海底声学参数的反演,并针对反演结果进行了后验概率分析,同时针对沉积层的反演结果,改进后的算法能够较好地反演出实验海域海底特性,与现有文献进行了对比,吻合较好。
[1] SIDERIUS M, HARRISON C H, PORTER M B. A passive fathometer technique for imaging seabed layering using ambient noise[J]. J. Acoust. Soc. Am., 2006, 120(3): 1315-1321.
[2] SIDERIUS M, SONG H, GERSTOFT P. Adaptive passive fathometer processing[J]. J. Acoust. Soc. Am., 2010, 127(4): 2193- 2200.
[3] QUIJANO J E, DOSSO S E, DETTMER J. Bayesian geoacoustic inversion using wind-driven ambient noise[J]. J. Acoust. Soc. Am., 2012, 131(4): 2659-2667.
[4] QUIJIANO J E, DOSSO S E, DETTMER J, et al. Trans- dimensional geoacoustic inversion of wind-driven ambient noise[J]. J. Acoust. Soc. Am., 2013, 133(1): 47-53.
[5] 殷宝友, 马力, 林建恒. 浅海环境噪声垂直指向性探测海底参数[J]. 应用声学, 2011, 30(1): 31-36. YIN Baoyou, MA Li, LIN Jianheng. Geo-acoustic surveying for seabed parameters using vertical directionality of ambient noise in shallow water[J]. Applied Acoustics, 2011, 30(1): 31-36.
[6] 李风华, 刘姗琪, 王璟琰. 台风激发水下噪声场的建模及其在台风风速反演中的应用[J]. 声学学报, 2016, 41(5): 750-757. LI Fenghua, LIU Shanqi, WANG Jingyan. A numerical model of underwater noise generated by typhoons and application in estimation of typhoon wind speed[J]. Actc Acustica, 2016, 41(5): 750- 757.
[7] 于盛齐, 黄益旺, 宋扬. 应用表面噪声矢量场空间相关特性反演海底参数[J]. 哈尔滨工程大学学报, 2012, 33(7): 828-833. YU Shengqi, HUANG Yiwang, SONG Yang. Geoacoustic parameter inversion using the spatial correlation of an acoustic vector field of surface-generated noise[J]. Journal of Harbin Engineering University, 2012, 33(7): 828-833.
[8] 王银年. 遗传算法的研究与应用——基于3PM交叉算子的退火遗传算法及应用研究[D]. 无锡: 江南大学, 2009. WANG Yinnian. The research and application of genetic algorithm-3PM crossover operator based annealing genetic algorithm and the research of its application[D]. Wu Xi: Jiangnan University, 2009.
[9] VASCONCELOS J A, RAMIREZ J A, TAKAHASHI R H C, et al. Improvements in genetic algorithms[J]. IEEE Trans. Magnetics. 2011, 37(5): 3414-3417.
[10] GU W J, ZHANG R C, ZHAO H C. On fuzzy sliding mode guidance based on self-adaptive genetic annealing algorithm[J]. IEEE Trans on SMC, 2008, 3(11): 2576-2581.
[11] HOLLAND J H. Adaptation in natural artificial systems[M]. MIT Press, 1975: 1-17.
[12] GOLDBERG D E. Genetic algorithm in search, optimization, and machine learning[M]. MA Publisher: Addison-Wesley, 1989: 2104- 2116.
[13] 向长城, 黄席樾, 杨祖元, 等. 小生境粒子群优化算法[J]. 计算机工程与应用, 2007, 43(15): 41-43. XIANG Changcheng, HUANG Xiyue, YANG Zuyuan, et al. Niche particle swarm optimization algorithm. Compuuter Engineering and Application, 2007, 43(15): 41-43.
[14] MANUEL L, FRANCISCO H, JOSÉ R C. Replacement strategies to preserve useful diversity in steady-state genetic algorithms[J]. Information Sciences, 2008, 178(23): 4421-4423.
[15] MILLER B L, SHAW M J. Genetic algorithms with dynamic niche sharing for multi-modal function optimization[C]//IEEE International Conference on Evolutionary Computation, 1996: 786-791.
[16] HUANG M, LIU N, LIANG X. An improved niche genetic algorithm[C]//IEEE International Conference on Intelligent computing and intelligent systems, 2009: 291-293.
[17] 林建恒, 高天赋. 简正波-射线混合风关海洋环境噪声模型[J]. 声学技术, 2003, 22(s2):119-121. LIN Jianheng, GAO Tianfu. A hydrid wind-generated noise model of normal mode and ray. Technical Acoustics, 2003, 22(s2): 119-121.
[18] 金翔龙. 东海海洋地质[M]. 北京: 海洋出版社, 1992: 185-196. JIN Xianglong. Marine geology of east china sea[M]. Beijing: China Ocean Press, 1992: 185-196.
Application of improved genetic algorithm in ambient noise based geo-acoustic inversion
CHEN Bo1,2, ZHAO Mei2, HU Chang-qing2
(1. University of Chinese Academic of Science, Beijing 100190, China;2. Shanghai Acoustic Laboratory, Chinese Academic of Sciences, Shanghai 201815, China)
Using ambient noise in shallow water to do geo-acoustic inversion is one of the hot topics. When considering double-layer bottom, the traditional genetic algorithm often makes the inversion process fall into the local minimum value, and the global optimal solution can not be found. In this paper, the expression of the spatial coherence of ambient noise field is calculated in the case of double-layer bottom, and the performance of the inversion algorithm is improved by introducing adaptive crossover operator, adaptive mutation operator, and niche technology which can keep the population diversity. Numerical simulation is carried out to verify that the improved algorithm has better performance of converging to real values than the traditional algorithm. Finally, the sea trial data are used to inverse seabed acoustic parameters and the result is relatively good.
genetic algorithm; niche technology; ambient noise in shallow water; geo-acoustic inversion
O427.9
A
1000-3630(2018)-01-0025-07
10.16300/j.cnki.1000-3630.2018.01.005
2017-11-07;
2018-01-29
上海市扬帆计划资助项目(15YF1414900)
陈勃(1991-), 男, 河南洛阳人, 回族, 博士研究生, 研究方向为海洋环境噪声。
胡长青, E-mail: hchq@mail.ioa.ac.cn
