超声波综合实验装置的设计与研制
2018-04-11彭国华熊永红李泰强
彭国华, 熊永红,2, 李泰强, 倪 昀, 丁 浩
(1.文华学院 基础学部,武汉 430074;2.华中科技大学 物理学院,武汉 430074)
0 引 言
声波是一种机械波,它可以在气态、液态、固态物质中传播。人耳能听到的声波频率在0.02~20 kHz,超声波在媒质中传播时,声速、声衰减和声阻抗都和媒质的特性及状态有关,通过测量这些声学量可以探知媒质的特性和状态变化。这些声学量的测量方法是超声无损检测、超声雷达、超声成像等实验基础。超声波的特性和测量方法在科学研究、医疗诊断和治疗、工业生产、日常生活等各方面都有广泛应用。因此,研究超声波的基本特性和测量方法有着非常重要的现实意义和价值。
本文结合湖北省大学生物理实验创新设计竞赛,研制了一种超声波综合实验装置,该装置不仅可以完成超声波速度的测量,还可以观测和研究超声波在传播过程中的反射、透射、折射、布拉格衍射现象和规律,测量超声波在不同材质中的折射率和模拟X射线衍射,测量“晶体模型”的晶格常数,测量超声波在不同材质中的衰减情况。该项目2016年已经获得第四届光驰杯湖北省大学生物理实验创新设计竞赛一等奖。
1 装置设计与研制
超声波在介质中传播具有反射、透射、吸收、折射、干涉和衍射等物理现象,在传播过程中遇到障碍物,超声波的传播方向和声强分布会发生改变。因此我们设计了一个基于精密测角仪、两个相互垂直的线性测长仪、超声波发射和接收系统等模块,构建组合式超声波综合实验装置。将超声波发射器和探测器分别固定在该装置的发射架和测试架上,就可测量超声波声强在三维空间的分布。
该综合实验装置框架由以下几部分组成:超声波发射系统、超声波接收系统,超声波测量系统、载物台、实验介质和超声波元器件、信号源和示波器。
精密测角仪由底座、中心轴、游标盘和刻度盘构成,其结构如图1所示。刻度盘采用圆形设计,游标采用半圆或圆弧设计,增大刻度盘和游标盘直径,细分最小分度值,使角度测量的精度有所提高。超声波发射器安装在综合装置的发射架上,超声波发射器在发射架上的高度可调。

图1 超声波综合实验装置结构示意图
超声波接收器安装在装置的测试架上,超声波接收器三维可调,在水平面绕中心轴左右转动,可以进行样品反射角、折射角或衍射角的精确测量;水平线性测长仪由主测量尺和游标构成,通过水平线性测长仪可以观测超声波的干涉现象,用共振干涉法或相位比较法测量超声波的传播速度;垂直线性测长仪的测量原理与水平线性测长仪原理相同,垂直线性测长仪与水平线性测长仪是正交结构,如图1所示。通过垂直线性测长仪可以测量超声波强度在垂直方向的分布。
水平测长仪与转动平台固定连接,与刻度盘和角游标共同构成精密测角仪。这样,就可以实现超声波某些性质的三维测量。
将该装置与示波器和信号源连接,将测量介质置于载物台上即可进行实验数据的测量,通过观察示波器波形幅值的强弱,记录数据,经理论计算与分析即可得出结论。
2 实验观测
2.1 单缝衍射法求超声波的波长
超声波具有衍射的特性,当超声波垂直入射单缝衍射模板后,在单缝后面便会出现超声波的单缝衍射图样,即超声波声强出现强弱分布的现象,如图2所示。

图2超声波单缝衍射示意图
衍射图样中极小值对应的角度θ:
asinθ=kλ,k=1,2…
(1)
式中:a表示缝宽;k表示级次;θ是衍射超声波束与单缝模板法线的夹角,称为衍射角;λ表示超声波的波长。
衍射强度随超声波接收端转动角度变化,寻找波形峰值极小值点,即衍射强度最弱的位置,读出接收装置转动的角度θ,将其代入式(1)即可算出超声波的波长。将测量的波长与理论波长相比较即可求出实验误差。
2.2 布拉格衍射
实验所用的测量样品为简单立方晶体模型,其结构就是一个三维光栅,超声波通过该三维光栅就会产生布拉格衍射。当超声波入射方向与某个晶面成一定夹角时,会产生光程差,当光程差等于波长的整数倍时,此时晶面的衍射分布就满足布拉格方程:
(2)
式中:d为晶面间距。对于一个三维晶体模型,在水平方向上,可以利用精密测角仪准确测量出超声波对应某个晶面的衍射角θ,代入式(2)即可算出晶面间距d,再将实验测得的d测与模型的标称值d标进行比较即可得出实验误差。同理,在竖直方向上通过竖直的测量尺和示波器找到满足衍射极大值的位置,测出此方向的相对距离,再测量出两超声波压电换能器探头距离,利用三角函数算出θ,代入布拉格方程即可算出竖直方向上的晶面间距,对于第三维方向上的晶面间距,只需将晶体模型在水平方向上转动90°重复上述实验方法即可算出第三方向的晶面间距d。
图3所示为布拉格衍射中的简单立方结构晶体模型,晶面间距为21.00 mm。

图3 简单立方结构晶体模型示意图
2.3 利用超声波测量不同材料的折射率
不同材料对同一频率的超声波其折射率是不同的。通过自制泡沫材质的正三棱柱和PLA材质的正三棱柱作为待测样品,用超声波综合实验装置对泡沫和塑料样品的折射率进行测量。超声波发射方向与三棱柱某一面成一定角度,慢慢转动超声波接收端,寻找示波器上幅值极大值点,找到极大值点后,记下刻度盘读数,再将接收端转到和发射端轴线平行的位置,记下刻度盘读数,两数相减即为最小偏向角δ,即可算出折射率n(三棱柱的顶角A=60°),实验原理如图4所示。
(3)

图4超声波折射率测量示意图
3 实验数据
3.1 单缝衍射法求超声波波长
超声速在空气中的传播速度与空气中的湿度和环境的温度有关,本次实验在干燥下的环境下进行,室内温度24 ℃。由超声波在空气中的传播速度的理论值可由下式计算:
(4)
式中:v0为t=0 ℃时的声速,v0=331.5 m/s;T为环境热力学温度。根据式(4)求出声速vT,由速度与波长的关系可以算出超声波的波长。由该式可以算出24 ℃下的声速为345.76 m/s,实验中超声波换能器发射端的发射频率为40.566 kHz,则由λ=v/f即可算出理论波长λ理=8.52 mm。
表1为单缝衍射法测超声波波长的实验数据,表中θ0为发射端超声波换能器中心轴线与接收端超声波换能器中心轴线共线时接收端所处的初始角度位置,为转动接收端示波器出现极小值时接收端所处的角度位置,θ为衍射角,由以上数据可测出出现一级极小衍射测出λ1为8.53 mm,误差为0.2%;二级极小衍射测出λ2为8.57 mm,误差为0.6% 。

表1 单缝衍射法求超声波波长数据表(a=25 mm)
3.2 布拉格衍射
布拉格衍射数据见表2、3。由布拉格方程(2)可知,求解模型的d需知超声波长λ,取λ理=8.52 mm,为已知量。θ1实验开始前超声波发射端换能器中心轴线与接收端换能器中心轴线共线时初始角度θ0=251°50′。当转动接收端观察示波器第一次出现极大值时,记下θ极大,即可算出θ值,代入式(2)即可算出模型d测,d标为模型晶面间距的实际值,d测与d标相比即可算出相对误差。

表2 布拉格衍射数据表(水平方向100)

表3 布拉格衍射数据表(竖直方向001)
表3为布拉格衍射在竖直方向上的数据表,本实验用到的立方体模型是个三维模型,利用该装置可以进行三维测量的特点进行实验。先测量实验开始前发射端与接收端中心轴线共线状态下2个超声波换能器探头端面的距离l,同时记下接收端换能器在竖直游标上的初始位置d0,接着移动接收端,直到示波器第一次出现极大值,记下标尺读数d1,则衍射角
θ=arctan[(d1-d0)/l]
将θ代入式(2)即可算出d测。
3.3 利用超声波测量不同材料的折射率
为测不同材料的超声波折射率,本实验采用了两种材料,三棱柱顶角均为60°,由式(3)计算材料折射率。在进行泡沫折射率的测量实验中测得的超声信号极大值的临界角θ临=202°,初始位置θ0读数221°40′,则δmin=19°40′,算出泡沫的折射率为1.28。
同理,在进行PLA折射率的测量中测得θ临=184°35′,θ0=218°40′,则δmin=34°5′,算出PLA的折射率为1.46。
4 分析讨论
对于简单立方晶体模型的水平和垂直方向的晶格常数测量存在明显的误差,通过对装置的分析可知,问题主要出在衍射角度的测量上。水平测量采用的是精密测角仪,所以测量结果与标称值对比误差较小。而垂直测量衍射角存在较大的误差,其原因如图5所示。
图中:a表示缝宽;D表示从狭缝到超声波传感器的距离。因衍射角度较小,可以假设:sinθ≈tanθ。
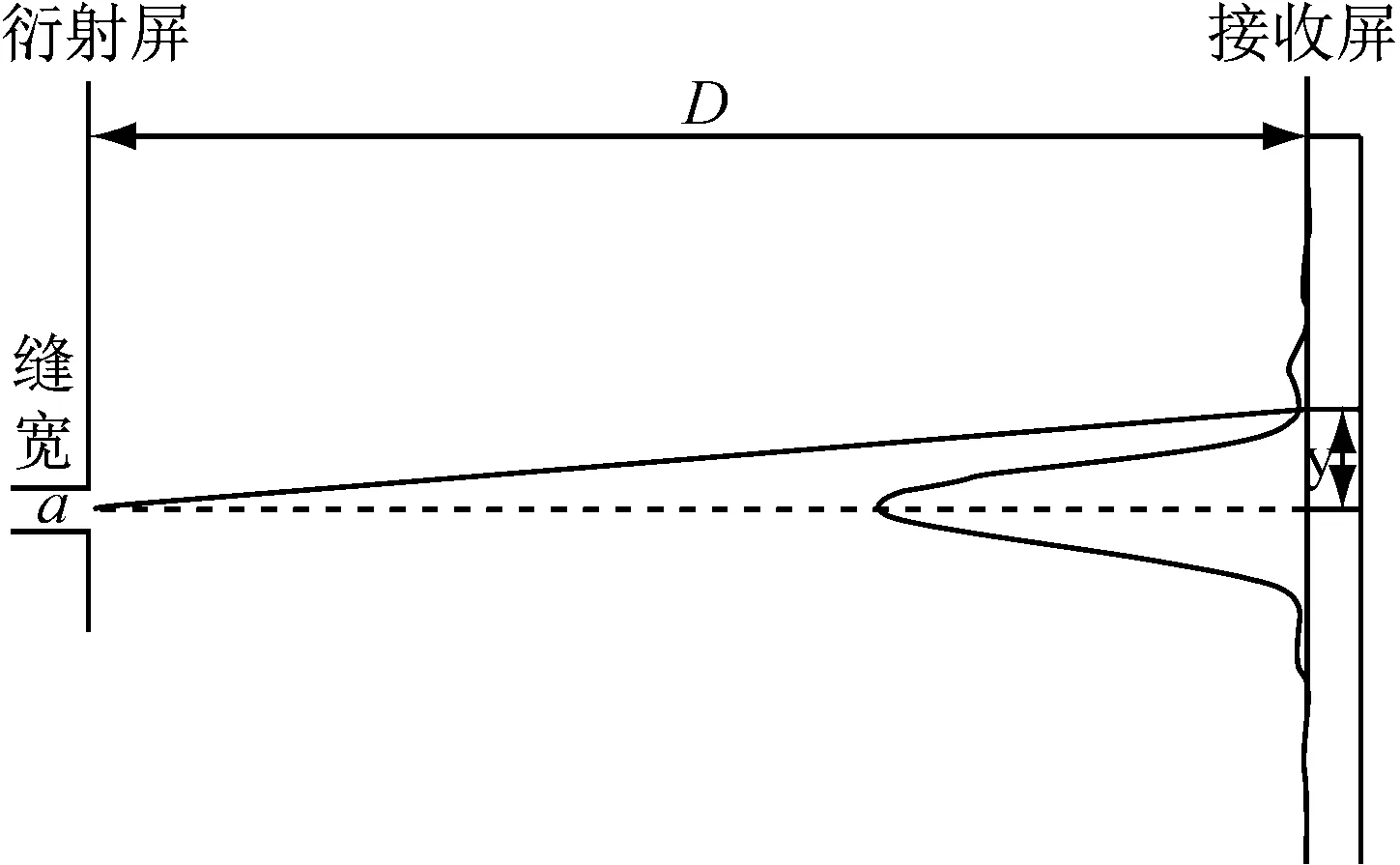
图5垂直测量示意图
根据三角关系有:
tanθ=y/D
(5)
a=kλD/y,k=1,2,…
(6)
正是由于sinθ≈tanθ这种三角关系的近似引入了实验的误差,使(001)方向的测量误差大于(100)的测量误差。通过将样品(001)方向旋转90°在水平方向进行测量,可使测量误差降低。
5 结 语
晶体微结构尺度在10-10~10-8m的范围,只有用SEM、STM、XRD等测量物质微结构的大型精密测量仪器,才能够对物质的微结构进行测量、分析和研究。但这些大型精密仪器价格昂贵,XRD还有辐射源,对测量环境和实验人员都有很高的要求,因此不可能用于本科生物理实验教学。用超声波实验装置对“晶体”模型进行测量,不仅让我们能直接观测 “晶体”结构,还可间接地学习XRD的测量原理,培养学生科学思维能力,学习用变量转换法和物理模拟法来设计新实验装置,将看不见的微观物理量转换为看得见的几何参量,用常规的超声波发射器模拟X射线源,避免了X射线辐射。
利用超声波综合实验装置,不仅可以进行超声波的反射、透射、折射、干涉和衍射等系列实验研究内容。同学们还可以在该装置上进行DIY实验内容的拓展,进行创新设计和探索性实验内容的研究。
参考文献(References):
[1]熊永红,张昆实,任忠明,等.大学物理实验(第一册)[M].北京:科学出版社,2007:117-123.
[2]赵荒培. 钢材中超声波衍射的布拉格(Bragg)方程应用[J]. 物理测试,2014(5):59-62.
[3]王敏. 分光计最小偏向角法测量方案及其误差产生原因与改进[J]. 电子测试,2014(2):39-40+9.
[4]王晓颖,王涛,李武军. 超声光栅实验中声致折射率变化的研究[J]. 大学物理,2012(5):50
[5]袁仁福. 超声波技术的现状和发展趋势[J]. 世界科学,1993(1):35-39.
[6]吕令杰. 匀速运动介质中的声波干涉[J]. 大学物理,2016(2):52-55.
[7]孙艳,于丹,王广. 利用布拉格衍射模拟信号传输[J]. 科技信息,2010(6):113-114.
[8]何颖卓,李春芝. 微波布拉格衍射实验中测量衍射极大值的新方法[J]. 大学物理实验,2013(5):9-12.
[9]傅崧原. 一种水波声波干涉实验装置[J]. 科技创新与应用,2013(36):55.
[10]刘战存,苑红霞. 布拉格父子对X射线晶体衍射的研究及其启示[J]. 首都师范大学学报(自然科学版),2006(1):32-36.
[11]曹连振,刘霞,张莹,等. 分光计测最小偏向角法内容的延伸及数据处理的改进研究[J]. 潍坊学院学报,2012(2):76-78.
[12]袁哲峰. 分光计测量三棱镜折射率的误差分析[J]. 科技资讯,2006(16):2-4.
[13]李昂,王建锋,刘洋. 分光计测量三棱镜顶角实验的两学时课堂教学探讨[J]. 教育教学论坛,2014(38):248-249.
[14]邬融,田玉婷,赵东峰,等. 透射衍射光栅内全反射级次[J]. 物理学报,2016(5):106-114.
[15]Kessler L. Ultrasonic visualization by pulsed bragg diffraction: U.S. Patent 3,737,573[P]. 1973-6-5.
[16]Santiago J G, Dutton J C. Velocity measurements of a jet injected into a supersonic crossflow[J]. Journal of Propulsion and Power, 1997, 13(2): 264-273.
