大跨度多塔斜拉桥行波效应分析
2018-04-11姜哲勋
姜哲勋
(西南交通大学桥梁工程系,四川成都 610031)
通常对大跨度斜拉桥采用一致激励法进行结构地震响应分析。一致激励法指的是假定基础在地震作用下各点以相同的振幅和相位振动,地震地面运动输入的是与抗震设防目标相对应的地震加速度时程。
实际地震波传播速度有一定范围,通常在每秒数百米至每秒数千米的范围内。当桥梁支座间距很大时,地震波到达各支座的时间差异较大,导致各支承处输入地震时程产生明显的相位差,即行波效应。对于大跨度斜拉桥,这类现象更加凸出。
众多工程实例表明,考虑行波效应下的斜拉桥结构地震响应与一致激励下的地震响应有一定差异。范立础[1]等对南京长江二桥进行研究,结果表明波速变化而引起的大跨度斜拉桥地震反应的变化可以达到40 %;A.M.Ghaffar和H.H.Nazmy[2-3]等对两座不同跨度的斜拉桥进行考虑行波效应下的地震反应研究,结果表明考虑行波效应对结构位移和内力响应有增大趋势,斜拉桥刚度大和场地地质条件差情况下影响更显著;国内外学者[4-7]还对行波效应问题进行大量研究,得到的结论也不尽相同。行波效应对于大跨度斜拉桥的影响比较复杂,还需进一步完善。本文结合某大跨度四塔斜拉桥,研究行波效应对其地震响应的影响规律。
1 行波效应计算方法
结构在各支承处受到地面运动作用的运动方程写成分块矩阵的形式为[8-9]:
(1)
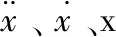
基于拟静力位移的概念,将结构的反应位移分解为动力反应位移xd和静力反应位移xs。
x=xs+xd
(2)
计算拟静力分量xs时不考虑惯性力项和阻尼项,可由式(1)计算得到:
xs=-K-1Kcu=Ru
(3)
式中:R=-K-1Kc为影响矩阵。
将式(2)和式(3)代入式(1),动力反应位移xd可以表示为:

次日周暄酒醒过来后,觉得自己的行为没有任何差池,他觉得那个同事说的话就是对他的挑衅,他必须维护妻子,维护他的尊严。
≈-(MR+Mc)u
(4)
由于阻尼力较惯性力小得多,因此式(4)可忽略此项,当阻尼矩阵与刚度矩阵成比例关系时,这种近似是可以的。此外,如果是集中质量模型,Mc=0。
2 斜拉桥有限元模型
以某大跨度四塔公铁两用斜拉桥为研究对象,该桥公铁同层合建。桥址处最大地震烈度为8度,工程场地类别为II类。主桥的跨径布置为(58.5+116+3×340+116+58.5) m。主梁采用挑臂式钢-混组合梁截面,顶宽49.6 m,底宽17.6 m,挑臂长16.0 m,组合梁中心梁高5.38 m(横截面最高点)。两中塔采用C60混凝土塔,两边塔采用Q345钢塔。结构体系采用刚构加连续梁方式,中塔塔梁墩固结;边塔塔梁固结,塔墩分离,梁底设双排支座,同侧两个为多向活动支座,另一侧两个为纵向活动支座。主墩采用双肢薄壁墩,边墩采用框架式墩,辅助墩采用桩柱墩,边墩及辅助墩横向设置两个支座,一个为多向活动支座,另一个为纵向活动支座。
运用Midas有限元程序建立全桥三维空间有限元模型。模型中主塔、主梁、桥墩均采用空间梁单元模拟,其中主梁采用单梁式力学模型,并通过主从约束与斜拉索面形成“鱼骨式模型”;斜拉索采用空间桁架单元,拉索与主梁及主塔均采用刚性连接;各处基础底部采用固结模拟。主梁与过渡墩、辅助墩和主塔的纵向活动支座在纵向相对自由,横向主从约束,双向活动支座在纵向和横向均相对自由。动力计算模型见图1,主塔结构见图2。

图1 动力计算模型
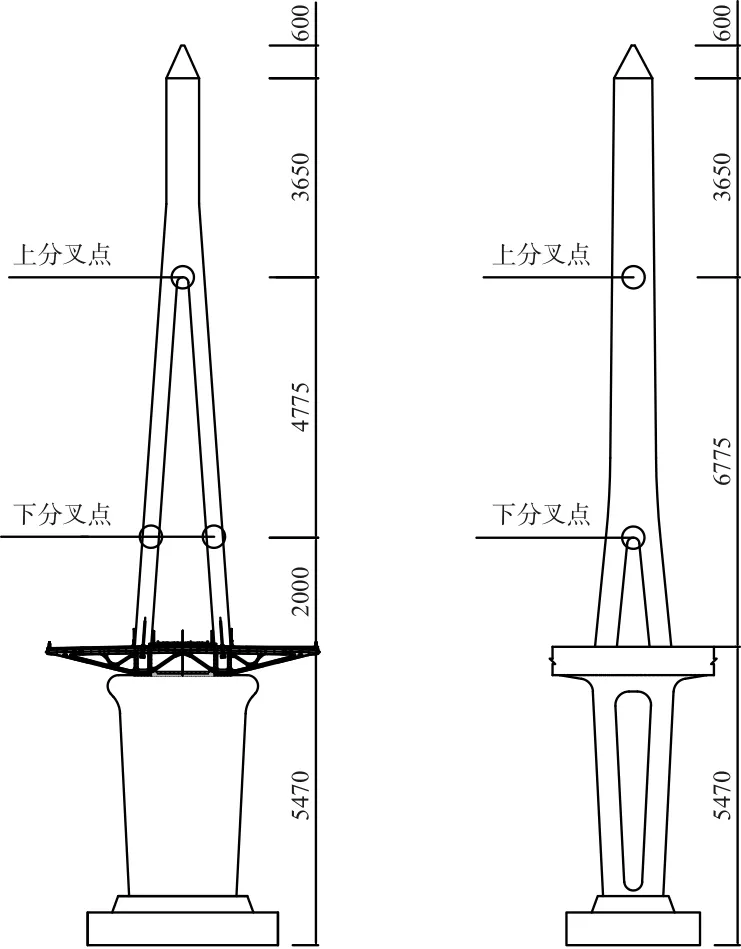
(a)主塔侧视 (b)主塔正视图2 主塔结构(单位:cm)
3 桥址场地地震动输入
根据结构场地条件,选取工程安评报告提供的加速度时程数据作为输入地震动。采用最不利的罕遇地震(PGA为0.2g)作用下进行研究。
地震组合方式采用纵向+竖向和横向+竖向;竖向地震作用取相应水平地震作用的0.65。图3表示50年超越概率2 %的3条地震波中的一条。采用时程分析法,取3条地震波最大反应值作为最终输出。

图3 加速度时程曲线
4 结果分析
本文以波速即地震传播速度为出发点,考虑由此引起的行波效应对多塔斜拉桥的地震响应影响规律。本文主要对地震波的纵向输入进行讨论,同时也不考虑桩-土-结构相互作用。
假定地震波从桥梁左岸传到右岸,取视波速v为50 m/s、500 m/s、1 000 m/s、1 500 m/s、2 000 m/s、2 500 m/s、3 000 m/s、4 000 m/s、6 000 m/s、8 000 m/s,计算此时的结构地震响应,和只考虑纵向地震波输入的一致激励的情况做对比分析。
4.1 动力特性分析
认识结构动力特性是抗震分析的基础。采用多重Ritz向量法,对主桥进行动力特性分析。表1列出前10阶主要的自振频率和主振型。
由表1可知,该桥第一阶出现主梁对称竖弯,符合斜拉桥支承体系的特征。该桥的自振周期长,柔度大;频率相差小,频谱密布。
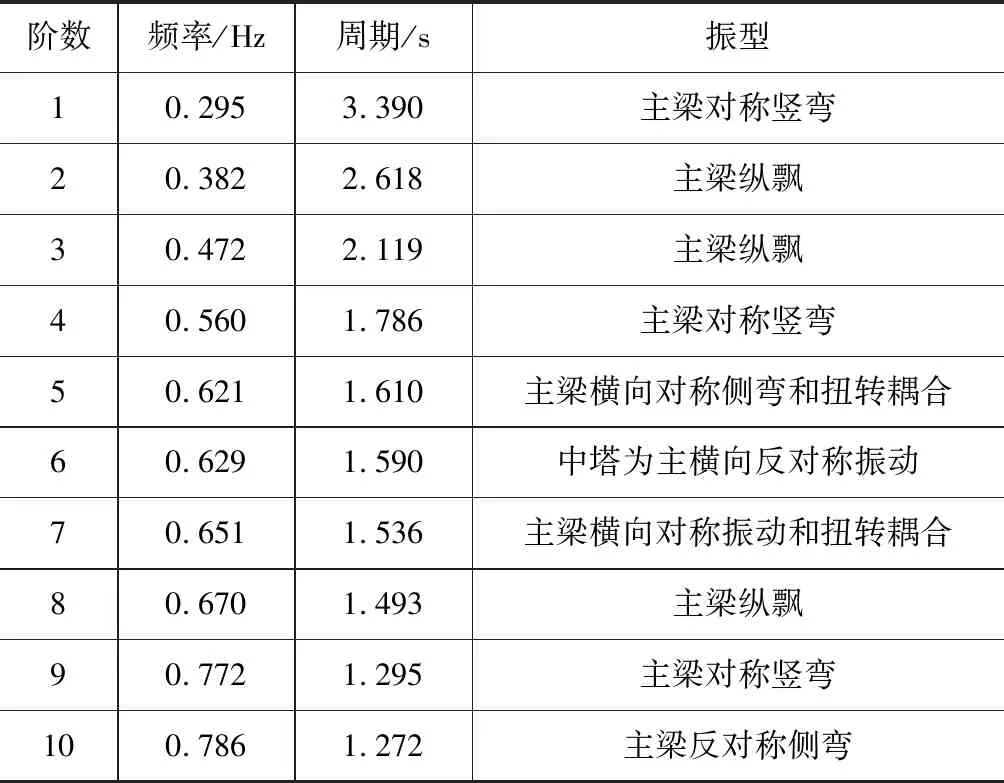
表1 模型动力特性
4.2 位移结果分析
图4~图6给出了在不同波速条件下,行波效应对梁端和塔顶的位移影响。为便于比较不同波速下关键位置的位移响应和一致激励情况的关系,图中竖坐标表示两者之间的位移响应极值的比值。
由图4~图6可知,波速对桥梁关键位置的影响有如下规律及相应结论:
(1)约在小于1 000 m/s的波速段,结构的纵向位移响应表现出增大趋势,这是由于行波效应激起了斜拉桥对称振型的参与[10],这对结构位移影响是不利的。在波速大于1 000 m/s后,结构位移与一致激励作用下的地震位移响应基本相同。
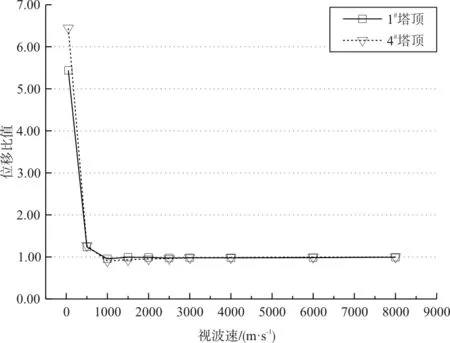
(a)边塔塔顶(1#塔和4#塔)纵向位移

(b)中塔塔顶(2#塔和3#塔)纵向位移图4 波速对塔顶纵向位移的影响

图5 波速对梁端纵向位移的影响
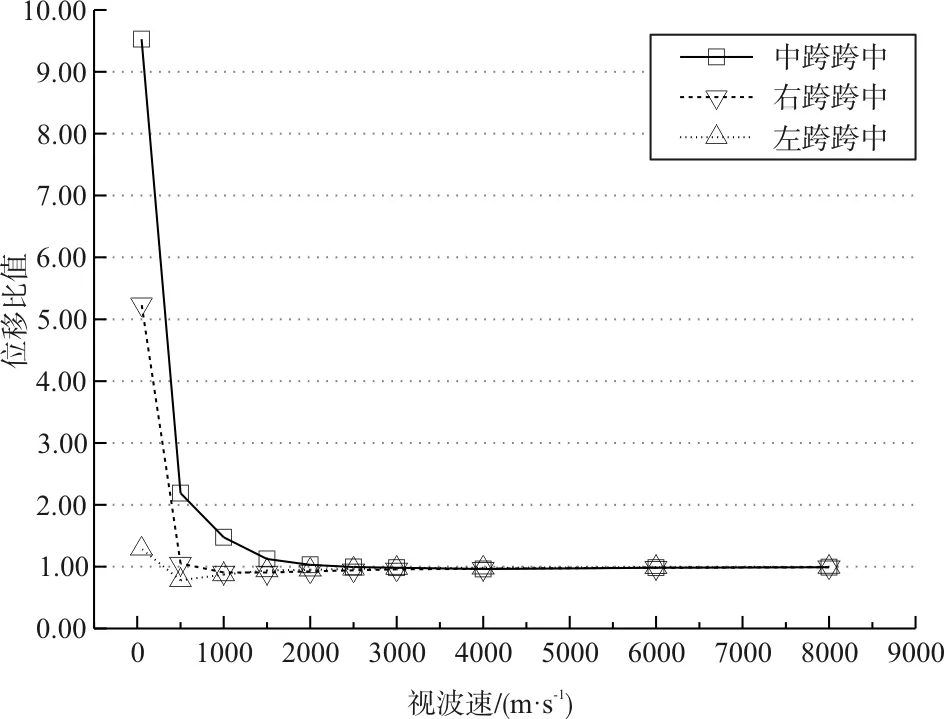
图6 波速对跨中纵向位移的影响
(2)由图6可知,其中波速对左跨跨中纵向位移影响最大,再依次是中跨跨中、右跨跨中,正好是沿地震波传播方向影响依次减小。考虑行波效应的情况下,结构位移响应对地震波传播方向也有一定影响。故在对结构进行抗震分析时有必要考虑行波效应的影响,并酌情考虑地震波传播方向的影响。
4.3 内力结果分析
图7~图10给出了在不同波速条件下,行波效应对主塔底和主墩底的内力(剪力和弯矩)影响。为便于比较不同波速下关键位置的内力响应和一致激励情况的关系,图中竖坐标表示两者之间的内力响应极值的比值。

(a)边塔塔底(1#塔和4#塔)剪力

(b)边塔塔底(1#塔和4#塔)弯矩图7 波速对边跨塔底的影响
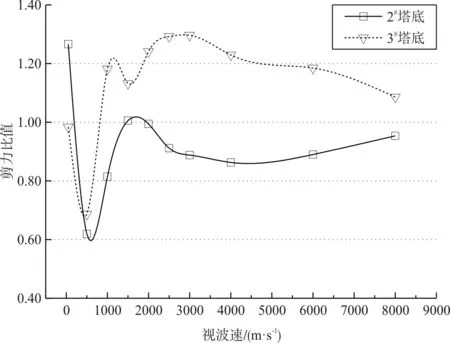
(a)中塔塔底(2#塔和3#塔)剪力

(b)中塔塔底(2#塔和3#塔)弯矩图8 波速对中跨塔底的影响
由图7~图10可知,波速对桥梁关键位置的影响有如下规律及相应结论:

(a)边主墩墩底(1#塔和4#塔)剪力
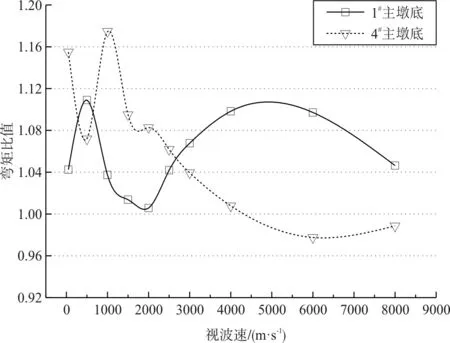
(b)边主墩墩底(1#塔和4#塔)弯矩图9 波速对边主墩墩底的影响
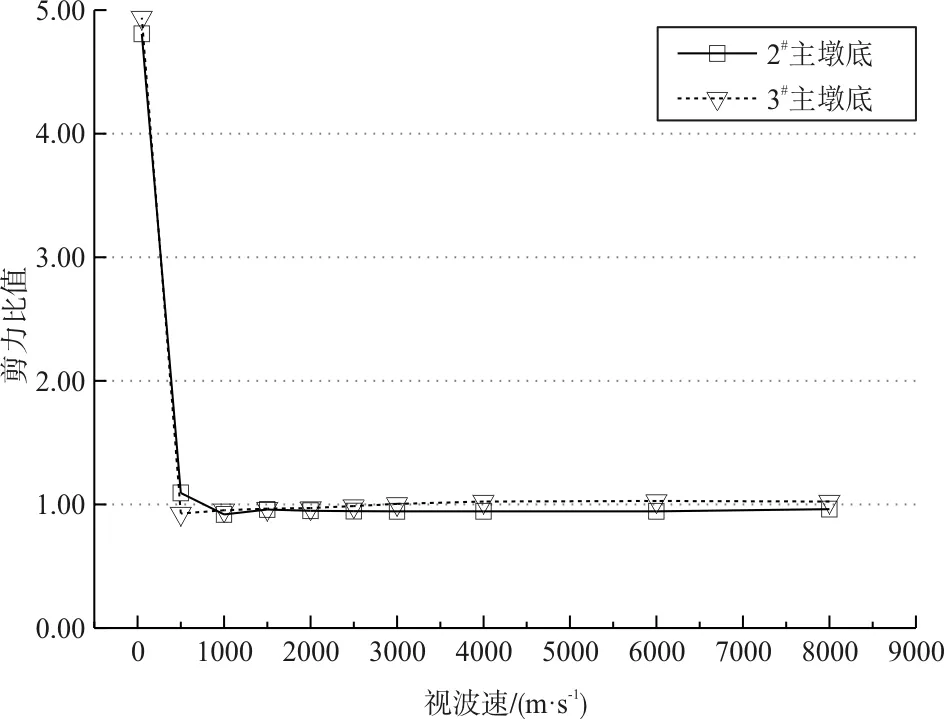
(a)中主墩墩底(2#塔和3#塔)剪力

(b)中主墩墩底(2#塔和3#塔)弯矩图10 波速对中主墩墩底的影响
(1)当波速较低时,行波效应会对结构内力产生较大的影响,而当波速逐渐增大时,结构内力响应也逐渐趋于一致激励作用下的地震内力响应。该大跨度四塔斜拉桥在波速约为500 m/s时会产生的结构内力极值,一般是结构内力的最小值。
(2)不同关键位置的内力响应量受行波效应的影响程度不同。就本文研究的大跨度四塔斜拉桥而言,边塔和边主墩的内力响应波动剧烈,中塔和中主墩内力能较快趋于一致激励。总体来说边塔内力在小于2 000 m/s的波速表现出减小趋势,边主墩内力在小于4 000 m/s的波速段表现出增大趋势;中塔和中主墩内力在小于500 m/s的波速段有增大趋势,且波速越小增大效果越明显。故特别注意考虑边主墩、中塔和中主墩内力在行波效应下的影响。
5 结论
本文结合某大跨度四塔斜拉桥的工程实例,计算结构在不同波速下的地震响应,并与只考虑纵向地震波输入的一致激励的情况做对比分析,研究行波效应对大跨度多塔斜拉桥地震反应的影响规律,主要结论如下:
(1)在低波速段,结构的纵向位移响应表现出增大趋势。地震波传播方向对部分结构位移响应也有一定影响。
(2)当波速较低时,行波效应会对结构内力响应产生较大的影响。该桥在波速约为500 m/s时会产生的结构内力极值,一般是结构内力的最小值。
(3)不同关键位置的内力响应量受行波效应的影响程度不同。波速对边塔和边主墩的内力响应波动更加剧烈,边塔内力在小于2 000 m/s的波速段有减小趋势,边主墩内力在小于4 000 m/s的波速段有增大趋势;中塔和中主墩内力在小于500 m/s的波速段有增大趋势,且波速越小增大效果越明显。
(4)在进行桥梁抗震设计时,有必要考虑低波速状态下的行波效应对结构地震响应的影响。
