目标跟踪时的雷达分级功率自适应控制

许 姣,张贞凯,田雨波

(江苏科技大学 电子与信息学院, 镇江 212003)

随着无源探测定位技术的发展,雷达生存能力受到挑战,提高雷达射频隐身的性能成为重要技术指标．在现代战场中,雷达很容易被截获和识别,射频隐身技术能较好地减小这个概率,实现雷达射频隐身是隐身作战的重要方面．雷达辐射功率越小,则辐射时间越短,雷达被截获的概率就越小．在满足跟踪精度的同时,通过发射最小的功率进一步提高雷达射频隐身性能．雷达资源合理控制是提高射频隐身性能的有效途径[1]．

目前,很多学者对辐射功率问题进行了深入研究[2-6]．文献[2]针对目标的距离和雷达横截面不断变化的问题,提出了对采样间隔和辐射功率设计方法,从而提高目标的跟踪性能．文献[3]提出了一种基于预测跟踪CRLB的相控阵雷达功率控制方法,在保证跟踪精度情况下,采用预测跟踪的(cramer rao low bound,CRLB)进行发射功率分配．文献[4]基于雷达(radar cross section,RCS)预测的方法,与建立功率分配的模型相结合,减小跟踪误差,且最终的测量值更加准确．文献[5]将多目标粒子群算法进行改进,且优化了阵元开关,有效地降低了辐射功率．文献[6]描述了射频隐身性能受辐射功率的影响,着重突出射频隐身的重要性．目前,交互多模型(interacting multiple model,IMM)具有较好的跟踪性能,从而获得了广泛应用[7-8]．

上述对发射功率的研究侧重于提高目标的跟踪性能,对目标跟踪时的功率控制研究尚未深入．文中基于协方差控制的思想,提出了一种自适应功率分级控制的目标跟踪算法,该算法根据目标距离的远近自适应地设计辐射的功率,以进一步提高雷达的射频隐身性能．

1 交互多模型IMM算法

交互多模型算法能够对目标进行合理地跟踪[9]．由于目标运动状态不相同,需选取不同模型进行匹配．其中,马尔科夫链表示不同模型间的转移概率,状态估计以及模型概率的更新使用各滤波器滤波的结果,将目标各模型的状态估计值进行加权求和得到总体估计[10-11]．IMM包括以下5个步骤:输入交互、模型滤波、模型可能性计算、概率更新和交互输出．

模型的状态方程和观测方程可表示为:

Xk=FXk-l+Uk-1

(1)

Zk=HXk-l+Vk

(2)

2 射频隐身的分级功率控制

2.1 辐射功率与目标跟踪精度的关系模型

在研究观测方程噪声的基础上,建立了辐射功率与目标跟踪精度的关系模型．

已知k时刻雷达方程如下:

(3)

通常情况下,相控阵雷达的距离测量为均匀分布,其标准差可由tk时刻的雷达距离分辨率Δr(tk)[4]确定:

(4)

采用单脉冲测角方式,角度测量的标准差为:

(5)

式(5)中,θ3dB为天线波束宽度;Km为常数,通常可取1.57;SNR(tk)为回波信噪比．

R(tk)=J·diag(tk)2,σa(tR)2,σe(tk)2·J

(6)

式中：

式中：σa(tk)为方位角的测量标准差；σe(tk)为俯仰角测量标准差；J为雅可比转换矩阵,从球坐标系转换为直角坐标系．

当雷达发射单脉冲信号,观测方程的测量噪声协方差矩阵可表示为:

(7)

由式(3～7)可以看出,雷达辐射功率和测量噪声协方差矩阵存在联系．

2.2 基于射频隐身的功率控制方法

在IMM算法的基础之上,研究雷达自适应辐射功率的设计(图1)．雷达辐射功率影响测量噪声协方差矩阵,辐射功率不同产生的测量噪声协方差矩阵不同．

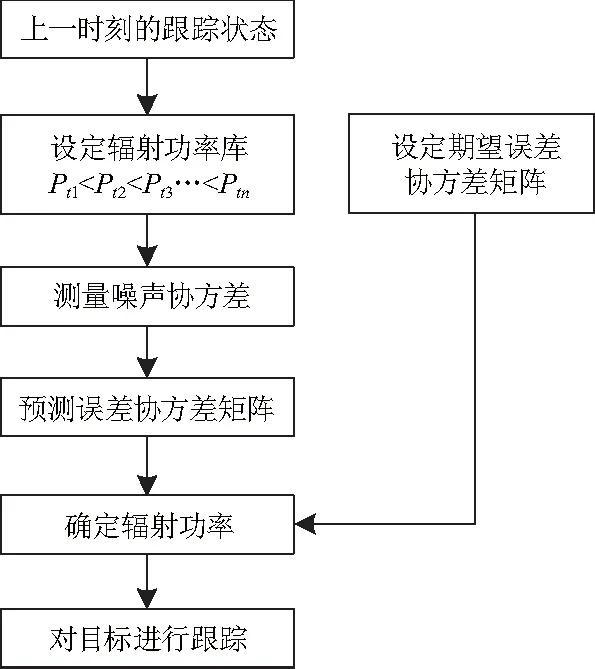
图1 辐射功率设计

如图1,分级功率自适应控制是在目标跟踪时完成．步骤如下:

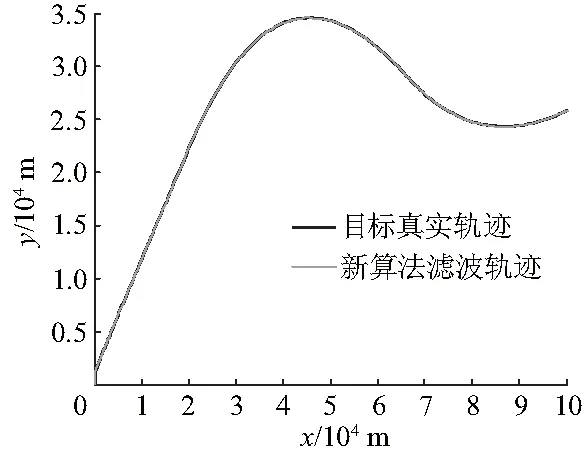
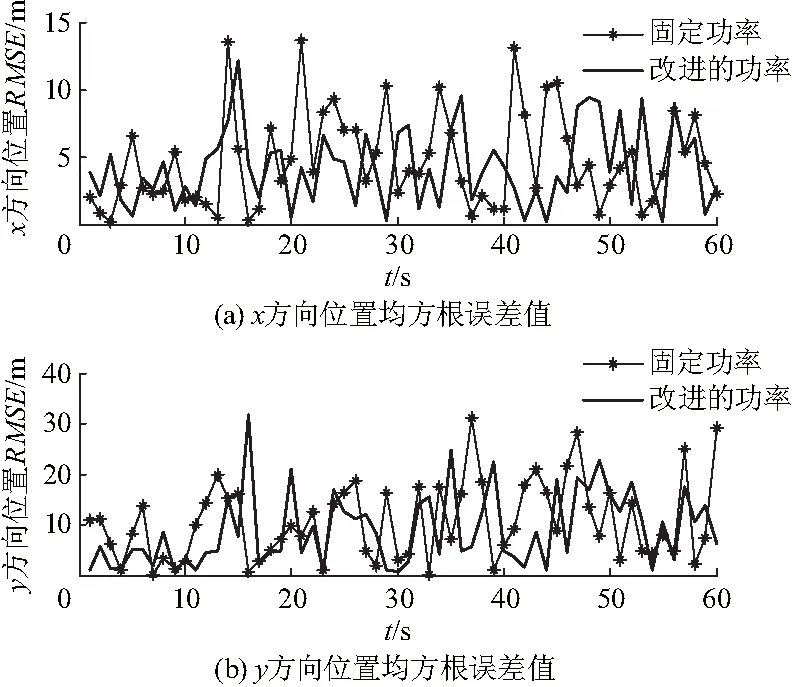
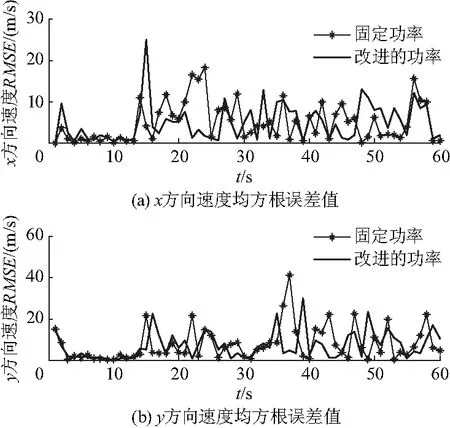
(1) 构造目标的运动轨迹．设定辐射功率库Pt={Pt1,Pt2,…,Ptn},且满足Pt1

(2) 根据目标不同时刻运动状态,设定初始状态变量,设定期望协方差．

(3) 确定一个辐射功率．由估计信息的总分配过程,计算模型的预测概率、模型的输入状态和误差协方差:

uk-1|k-1(i|j)

(8)

(9)

(10)

式中：

(11)

(12)

(13)

由式(13)可以看出,模型概率的大小受模型与运动状态匹配程度的影响,当二者匹配度较高时,模型概率就会比较大．反之,该模型概率就较小．

(14)

(15)

根据估算出目标的预测协方差矩阵,再选择预测协方差矩阵和期望协方差的值最接近的辐射功率对目标进行跟踪．

(4) 返回步骤(2),完成目标分级功率自适应控制．

3 仿真结果分析

为了进一步验证算法性能,采用Monte Carlo仿真模拟所提出的功率控制的性能．

根据IMM算法,将固定值的功率控制和自适应地功率控制进行了仿真比较．跟踪效果利用均方根误差(root mean square error,RMSE)和平均均方根误差(average root mean square error,ARMSE)作为评价标准,其定义分别为:

(16)

(17)

以跟踪目标在300 s内的运动轨迹来验证算法，假设建立辐射功率库(单位:kW),固定辐射功率为50 kW,IMM算法滤波模型中采用3个模型进行交互,选机动目标跟踪模型1为匀速直线运动,模型2为匀加速直线运动模型,模型3为转弯运动模型,模型初始概率为,马尔可夫概率转移矩阵:

目标的运动轨迹如图2,辐射功率仿真比较如图3,改进的辐射功率值大部分位于固定功率值水平线的下方,从仿真结果可以看出,自适应功率控制远小于固定的功率．目标位移误差和速度误差分别如图4、5,从仿真结果可以看出,算法具有较好的跟踪性能．为进一步量化算法的射频隐身和目标跟踪性能,仿真对辐射功率和跟踪误差等参数进行了量化比较(表1)，文中所提算法辐射的功率平均值小于固定值的辐射功率,由于采用协方差控制的思想对目标进行跟踪时的辐射功率进行控制, 根据目标机动性能、预测误差的不同设计不同的分级辐射功率,提出的算法在保证较好跟踪精度的同时,节省了雷达资源,即降低了辐射能量．

图2 目标的运动轨迹

图3 辐射功率仿真比较

图4 位移均方根误差

图5 速度均方根误差

表1 算法性能比较

从表1可以看出，文中算法与固定辐射功率时跟踪精度相差无几,论文提出的算法仅在x方向的位移跟踪精度较差,主要由于x方向目标运动机动性较强,算法在进行误差协方差估计时存在一定的误差．

4 结论

为了能够实现提高雷达的工作效率,研究雷达目标跟踪时的能量控制方法,提出了一种基于射频隐身的功率分级控制方法．

(1) 在研究交互多模型算法的基础上,建立了目标跟踪时雷达辐射功率控制模型．

(2) 基于协方差控制理论实现了雷达分级功率自适应控制,采用预测协方差和期望协方差最接近的辐射功率对目标进行跟踪,从而合理地分配了辐射功率．

(3) 在保证目标跟踪性能的基础上,所提算法降低了25%的辐射功率,具有较好的射频隐身性能,对实际系统设计具有一定指导意义．

References)

[1] 蔡茂鑫, 舒其建, 李勇华, 等. MIMO雷达射频隐身性能的评估[J]. 雷达科学与技术, 2013, 11(3): 267-270. DOI:10.3969/j.issn.1672-2337.2013.03.008.

CAI Maoxin, SHU Qijian, LI Yonghua, et al. Evaluation of RF stealth performance of MIMO radar[J]. Radar Science and Technology, 2013, 11(3): 267-270. DOI:10.3969/j.issn.1672-2337.2013.03.008.(in Chinese)

[2] 张贞凯, 周建江, 田雨波, 等. 基于射频隐身的采样间隔和功率设计[J]. 现代雷达, 2012, 34(4): 19-23. DOI:10.3969/j.issn.1004-7859.2012.04.004.

ZHANG Zhenkai, ZHOU Jianjiang, TIAN Yubo, et al. Design of sampling interval and power based on radio frequency stealth[J]. Modern Radar, 2012, 34(4): 19-23. DOI:10.3969/j.issn.1004-7859.2012.04.004.(in Chinese)

[3] ZHANG Z K, ZHU J. A novel power control method of phased array radar based on the predicted tracking Cramér-Rao Lower Bounds[C]∥Proceeding of the 2015 IEEE International Conference on Information and Automation, 2015:2888-2891.DOI:10.1109/icinfa.2015.7279780.

[4] 秦童, 戴奉周, 刘宏伟. 一种用于雷达资源管理的目标雷达截面积预测算法[J]. 电子与信息学报, 2015, 37(8): 1849-1854. DOI:10.11999/JEIT141466.

QIN Tong, DAI Fengzhou, LIU Hongwei. Radar cross section prediction method for radar resource management[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1849-1854. DOI:10.11999/JEIT141466.(in Chinese)

[5] 张贞凯, 周建江, 汪飞, 等. 基于射频隐身的相控阵雷达功率控制算法[J]. 系统工程与电子技术, 2012, 34(11): 2244-2248. DOI:10.3969/j.issn.1001-506X.2012.11.10.

ZHANG Zhenkai, ZHOU Jianjiang, WANG Fei, et al. Novel algorithm of power control based on radio frequency stealth[J]. Systems Engineering and Electronics, 2012, 34(11): 2244-2248. DOI:10.3969/j.issn.1001-506X.2012.11.10.(in Chinese)

[6] ZHAO S, CHENG T. Research on MIMO radar RF stealth algorithm in searching mode[C]∥2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), 2014:88-93. DOI:10.1109/icspcc.2014.6986158.

[7] 苗伟, 李昌玺, 吴聪. 基于修正转弯模型的交互多模型跟踪算法[J]. 现代防御技术, 2015, 43(3): 113-118. DOI:10.3969/j.issn.1009-086x.2015.03.021.

MIAO Wei, LI Changxi, WU Cong. Interactive multiple model tracking algorithm based on the modified model of turning[J]. Modern Defense Technology, 2015, 43(3): 113-118. DOI:10.3969/j.issn.1009-086x.2015.03.021.(in Chinese)

[8] WANN C D, SHIU J Y. Mobile target tracking and data fusion using dual-interacting multiple model system[C]∥2014 IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), 2014:1-6. DOI:10.1109/issnip.2014.6827699.

[9] 章飞, 孙睿. 基于粒子滤波的多传感器交互式多模型多机动目标跟踪[J]. 江苏科技大学学报(自然科学版), 2011, 25(6): 575-581. DOI:10.3969/j.issn.1673-4807.2011.06.015.

ZHANG Fei, SUN Rui. Interacting multiple model tracking algorithm of multiple sensor multiple maneuvering targets based on particle filter[J]. Journal of Jiangsu University of Science and Technology(Nataral Science Edition), 2011, 25(6): 575-581. DOI:10.3969/j.issn.1673-4807.2011.06.015.(in Chinese)

[10] 刘伟, 刘宁. 一种基于 UKF 交互多模型算法[J]. 雷达科学与技术, 2015, 13(3): 302-304,309. DOI:10.3969/j.issn.1672-2337.2015.03.016.

LIU Wei, LIU Ning. A UKF based interactive multi-model algorithm[J]. Radar Science and Technology, 2015, 13(3): 302-304,309. DOI:10.3969/j.issn.1672-2337.2015.03.016.(in Chinese)

[11] 封普文, 黄长强, 曹林平, 等. 基于自适应马尔可夫参数交互多模型算法的弹道导弹跟踪研究[J]. 兵工学报, 2014, 35(12): 2041-2049. DOI:10.3969/j.issn.1000-1093.2014.12.016.

FENG Puwen, HUANG Changqiang, CAO Linping, et al. Research on ballistic missile tracking based on adaptive markov parameter imm[J]. Acta Armamentarii, 2014, 35(12): 2041-2049. DOI:10.3969/j.issn.1000-1093.2014.12.016.(in Chinese)

[12] 卢建斌, 肖慧, 席泽敏, 等. 相控阵雷达波束波形联合自适应调度算法[J]. 系统工程与电子技术, 2011, 33(1): 84-88. DOI:10.3969/j.issn.1001-506X.2011.01.17.

LU Jianbin, XIAO Hui, XI Zemin, et al. Joint adaptive scheduling algorithm of beam and waveform for phased array radars[J]. Systems Engineering and Electronics, 2011, 33(1): 84-88. DOI:10.3969/j.issn.1001-506X.2011.01.17.(in Chinese)