基于神经网络和粒子群算法的大跨度钢管混凝土拱桥可靠度分析
2018-04-11岐峰军骆佐龙檀妹静
岐峰军,骆佐龙,姚 远,檀妹静
1.长安大学公路学院,陕西 西安 710064
2.山西大学土木工程系,山西 太原 030000
3.中国建筑设计院有限公司,北京 100044
4.北京临近空间飞行器系统工程研究所,北京 100076
钢管混凝土(CFST)拱桥已得到迅速发展和各种拓展应用,随之而来的是结构日趋复杂,忽略随机性的确定性分析已难以保障其安全可靠。大跨度钢管混凝土拱桥在某一特定失效模式下的极限状态函数很可能为高度的隐式非线性方程,传统可靠度方法难以胜任,日益发展的神经网络技术和优化技术恰好可以弥补上述不足。一方面,通过神经网络逼近显化,然后进行通过对显式化功能函数进行求解计算可靠度指标β。另一方面,传统方法(如JC法)求解可靠度指标只在轻度非线性的功能函数下易于收敛[1],对于强非线性问题则无能为力。与之相对,粒子群算法在非线性函数极值寻优方面具有突出优势:(1)采用神经网络可将隐式极限状态函数显式化,尤其适用于采用传统结构力学分析方法无法建立极限状态函数的复杂结构;(2)采用神经网络建立的极限状态函数可以逼近任意精度,尤其适用于非线程程度很高的情形;(3)采用粒子群算法计算极限状态函数可靠度指标,将可靠度指标的计算转化为目标函数的极值寻优,具有很好的全局搜索能力,计算出的可靠度指标能够满足任意精度要求。基于以上优势,将神经网络和粒子群算法相结合并推广到大跨度钢管混凝土拱桥这种复杂结构可靠度求解领域具有重要的实用价值。
1 BP神经网络基本原理
BP神经网络[2]结构如图1所示。单个神经元的数学模型为:



图1 单层BP神经网络模型Fig.1 One-layer BPneural network model
根据影响结构相应参数的随笔变量个数来确定输入神经元数量,输出神经元则根据工程需求由结构影响量确定,隐含层神经元数目可根据经验在满足计算精度而同时提供计算效率而定[3]。为了提高计算效率,样本点的生成可采用均匀设计法确定[4,5]。
2 粒子群算法应用原理
2.1 基本概念
粒子群算法[6-8]的基本原理为:针对目标函数的d个未知变量,在搜索阈中的n个随机运动的粒子,每个粒子位置用Xi=(xi1,xi2,…,xid)表示,相应速度用Vi=(vi1,vi2,…,vid)表示,每个粒子按如下方式进化:
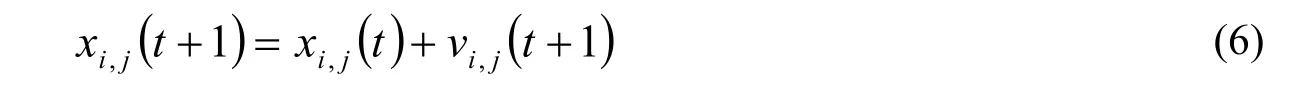
2.2 可靠度指标求解的数学模型
可靠度指标β的求解为一个极值函数的约束问题[9]:

求解时需要对随机变量进行预处理。
2.3 算法流程
PSO求解流程如图2所示。
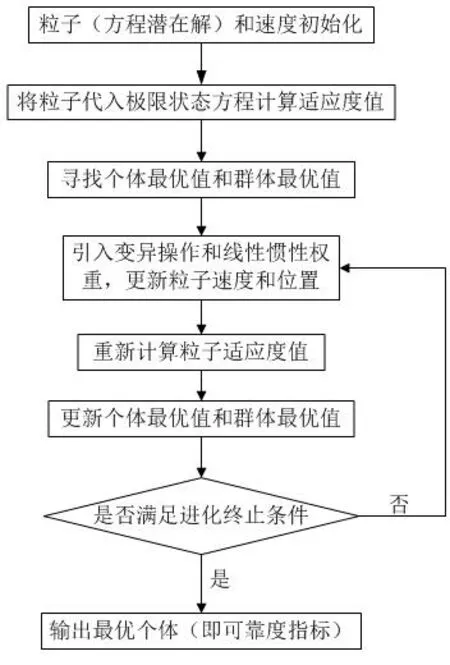
图2 基于粒子群算法的可靠度指标求解流程Fig.2 Reliability index solution procedure on PSO

图3 基于神经网络和粒子群算法的可靠度分析流程Fig.3 Reliability analysis procedure on neural network and PSO
3 大跨度CFST拱桥可靠度分析方法
可靠度分析过程如下(图3):
(1)明确随机变量及其统计参数,采用均匀设计生成样本点;
(2)根据样本点计算结构响应;
(3)神经网络学习样本,参照文献[12]得到显式化的极限状态函数;
(4)建立PSO模型;
(5)非线性寻优求解β。
4 算例验证

图4 算例图示Fig.4 The example layout
图4 框架极限状态方程为g(X)=0.01-μ3(X),μ3为点3水平位移。取3个随机输入:柱截面积A1、梁截面积A2和荷载P。A1、A2服从对数正态分布,P服从极值I型分布,参数为μA1=0.32 m2,σA1=0.036 m2;μA2=0.16 m2,σA2=0.018 m2;μP=20 kN,σP=5 kN;弹性模量为2.0×106Pa,惯性矩分别为
可靠度计算结果见表1,从中可以看出本文方法的优越性。算例为一个简单框架结构,但是计算原理与将复杂结构离散为有限单元进行计算本质上是一致的,因此,基于采用本文提出的方法进行同样适用于大跨度钢管混凝土结构可靠度分析准确性和有效性同样能够很好地满足工程要求,且非线性越强越能体现本文方法的优势。

表1 算例的计算结果Table 1 Calculation results from the example
5 工程应用及分析
5.1 工程概况
以健跳大桥为例。主跨245 m中承式CFST拱桥,矢跨比1/5,大桥立面如图5所示。
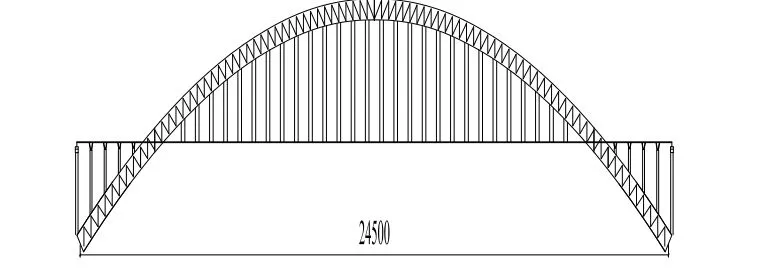
图5 健跳大桥立面布置(单位:cm)Fig.5 Elevation arrangement of Jiantiao Bridge(Unit:cm)
5.2 问题描述
本文分析采用ANSYS,区分是否考虑非线性。
式中:uL=L/1000=245/1000=0.245 m;x1,x2,…,xn为结构的随机变量。主要随机变量信息[12]如表2所示。
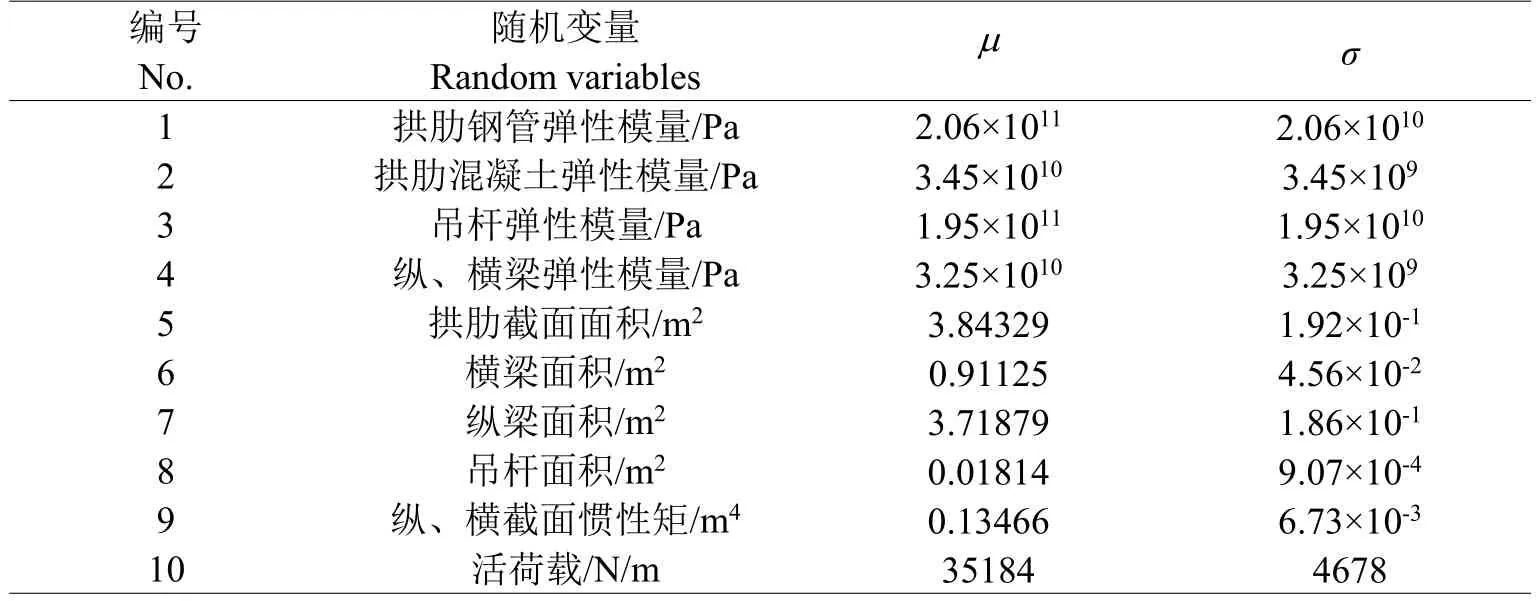
表2 结构主要随机变量基本统计参数Table 2 Statistics parameters of structural random variables
5.3 求解及分析
按照本文方法,建立11-11-1的三层BP神经网络,学习后求得显式化极限状态函数,可靠度指标求解依赖PSO算法。
不考虑几何非线性时,求解情况如图6。考虑几何非线性时,如图7。
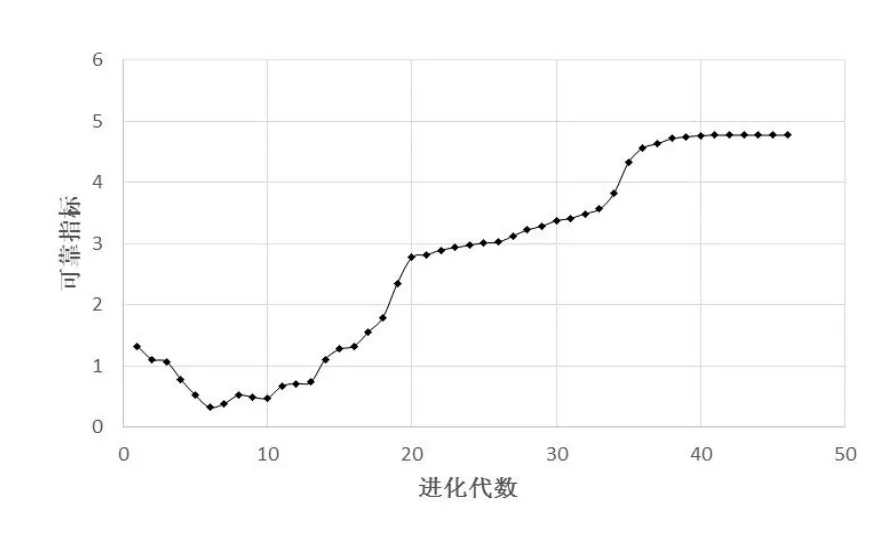
图6 线性分析求解Fig.6 Solution with linear analysis
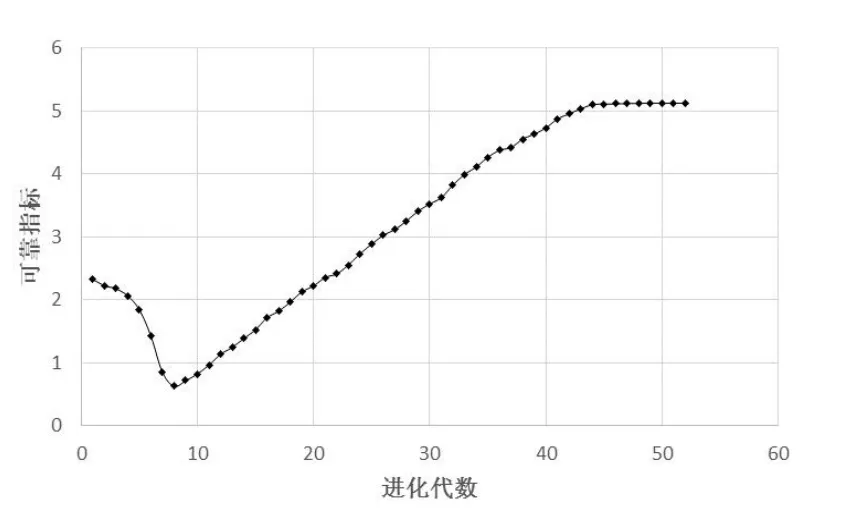
图7 非线性分析求解Fig.7 Solution with non-linear analysis
可见大跨度CFST拱桥正常使用极限可靠指标在考虑几何非线性效应(β=4.7758)比不考虑几何非线性效应(β=5.1271)降低了6.85%。因此须计入几何非线性。
采用本文方法同时计算了该桥承载能力极限状态可靠度指标,不考虑几何非线性时β=7.8531,考虑几何非线性时β=7.7912,二者相差仅0.79%,因此分析中可予以合理忽略。
6 结论
本文综合BP神经网络和PSO算法提出可靠度创新方法,并对大跨度CFST拱桥极限状态可靠度进行研究,结论如下:
(1)BP神经网络可以有效逼近并显化强非线性的极限状态函数;
(2)PSO算法的非线性寻优能力可以胜任复杂结构的可靠度指标求解,精确性较传统方法大幅提高,以很高的分析效率逼近精确的Monte Carlo模拟;
(3)在正常使用极限可靠度精确分析中,须计入几何非线性;在承载能力极限状态中则可合理忽略。
[1]贡金鑫.结构可靠指标求解的一种新的迭代方法[J].计算结构力学及其应用,1995,12(3):369-373
[2]Rumelhart DE,Hinton GE,Williams RJ.Learning Internal Representation by Error Propagation[J].Parallel Distributed Processing,1984(1):348-362
[3]巩春领.大跨度斜拉桥施工期风险分析与对策研究[D].上海:同济大学土木工程学院,2006
[4]方开泰,马长兴.正交和均匀实验设计[M].北京:科学出版社,2001
[5]粟 洪.大跨度悬索桥结构可靠度分析方法研究[D].上海:同济大学土木工程学院,2009
[6]杨 燕,靳 蕃,Kamel M.微粒群优化算法研究现状及其进展[J].计算机工程,2004,30(21):3-9
[7]Ratnaweera A,Halgamuge SK,Watson HC.Self-organizing Hierarchical Particle Swarm Optimizer with Time-varying Acceleration Coefficients[J].IEEE Trans on Evolutionary Computation,2004,8(3):240-255
[8]梁 军,程 灿.改进的粒子群优化算法[J].计算机工程与设计,2008,29(11):2893-2896
[9]张建仁,刘 扬,徐福友.结构可靠度理论及其在桥梁工程中的应用[M].北京:人民交通出版社,2003
[10]李扬海,鲍卫刚,郭修武,等.公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社,2007
