土石坝心墙裂缝发展的扩展有限元模拟

赵晓龙,卞汉兵,郑 威,孙兆辉,章赛泽,邱秀梅*

1.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098

2.河海大学 岩土工程科学研究所,江苏 南京 210098

3.山东农业大学 水利土木工程学院,山东 泰安 271018

4.LEM3,CNRS 7239，洛林大学,梅兹 法国 57045

5.徐州市水利建筑设计研究院,江苏 徐州 221112

土石坝水力劈裂是亟待解决的问题之一[1,2]。目前关于水力劈裂的数值模拟，学者们做了很多工作，如有限元、边界元和无单元法等，其中有限元应用最为广泛和成熟。李全明等[3]引入裂缝弥散理论来描述裂缝发展过程，从而实现水力劈裂的有限元模拟。王俊杰[4]等引入四节点等参单元建立裂缝及影响区的有限元模型，实现对裂缝的模拟。上述研究成果对于水力劈裂数值研究有很好的启发意义，但由于有限元法本身的缺陷，使其模拟裂缝开展遇到很多问题。

有限元在处理裂纹问题时，需要根据裂缝的位置分布网格，在裂尖区域需要分布密集的网格来反映应力的变化，当裂缝扩展时网格需要重新划分，因此计算效率很低，对于复杂的裂缝扩展问题甚至无法解答[5]。

在此背景下，Belytschko教授于1999年提出了扩展有限元法XFEM[6,7]，用以解决有限元难以解决的不连续问题，如裂纹扩展等。与常规有限元不同，扩展有限元分析裂缝时，网格无需重新划分，而是在包含裂缝的单元内增加自由度来描述不连续体的位移间断，位移间断通过富集函数来描述，可以显示裂纹的扩展路径，反映土体在流固耦合作用下变形特性，因而具有优越性[5,8]。

近年来，国内一些学者[9-12]开始将扩展有限元应用到混凝土坝体材料的开裂分析中，但土石坝粘土心墙水力劈裂的扩展有限元模拟鲜有报道。

本文基于扩展有限元，以损伤力学为理论基础，参照混凝土等材料的建模思路，考虑到基质吸力对黏土力学性能和裂缝发育的影响，建立了压实黏土的孔隙扩展模型和裂缝张开模型，对裂缝的发展进行了模拟。该思路对于土石坝的水力劈裂数值研究有一定的借鉴性。

1 心墙黏土水力劈裂模型

1.1 黏土孔隙扩展模型

1.1.1 模型本构关系 根据损伤力学理论，将土体内部的孔隙看作微裂纹（细观裂纹），土体由于微裂纹发展而产生类似损伤的演化，将土体模拟为连续介质，引入损伤变量，以热力学为基础，将孔隙的扩展视为能量转化的过程，由自由能和耗散势导出孔隙扩展的本构关系和演化方程，描述材料从孔隙扩展到出现宏观裂纹的过程。

压实黏土微裂纹演化的动力学特征在张拉和压缩应力作用下是不同的，为说明其演化对加载路径的依赖性，使用标量ωc、ωt表示微裂纹在受压和受拉情况下的演变。构造总体裂纹影响系数ω来表征两种裂纹对黏土力学性能的影响：

式中αt和(1-αt)用来描述张拉和压缩产生的微裂纹对材料力学性能总体影响的贡献率。αt的定义见下式：

于是，压实黏土的本构关系可以直接通过自由能函数，即方程导出：

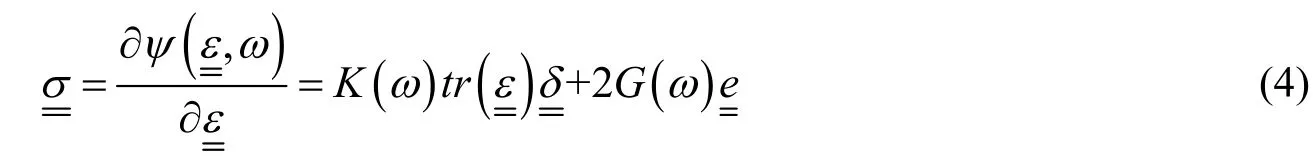
通过自由能函数，可推出两个损伤变量，即在受压和受拉状态的关联共轭热力学力：

1.1.2 孔隙扩展准则的建立 基于不可逆转的热力学过程，孔隙扩展需要一个适当的准则来决定。准则可以是损伤共轭力(见式)的函数。但这种准则难以通过试验测定，因而现实多采纳以物理学为依据的方法。由于微裂纹的形成和张拉应变之间存在固然联系，引入等效张拉应变的定义，有其中，iε代表i方向的主应变。括号表示只有x为正值才会被考虑，若x为负值或零，则〈x〉=0。将孔隙扩展驱动力定义为等效张拉应变加载历史中达到的最大值：Yω=max(εeq，Yhis)。Yω取等效张拉应变和加载历史中达到的最高值Yhis之间的最大值。这表明微裂纹的形成和扩展是一个不可逆的过程。

类似于混凝土材料中的Mazars模型，采用指数形式描述受拉和受压状态下微裂纹的演化过程：

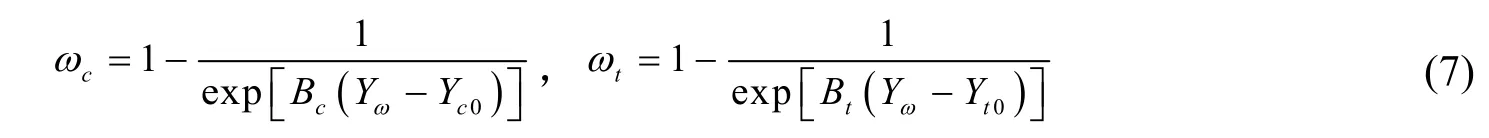
式中，参数Bc和Bt用来控制在压缩和张拉荷载条件下压实黏土微裂纹的演化速度，很明显Bt＞Bc，即在压实黏土中，受拉条件下微裂纹更容易形成和扩展。Yc0和Yt0定义为微裂纹的初始阈值。此外，ωc和ωt的演化法则应当验证中的能量耗散条件。

1.1.3 基质吸力对压实黏土孔隙演化的影响 在非饱和土中，还要考虑到负空压引起的基质吸力对材料力学性能及微裂纹发展的影响。在非饱和条件下，线弹性孔隙介质的本构关系可以表达为：

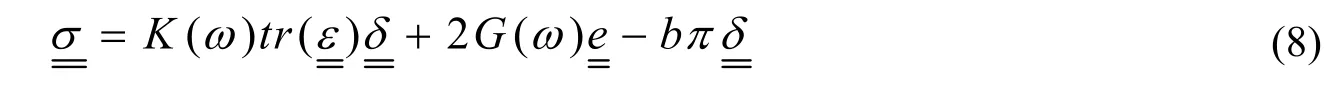
式中π是等效孔隙压力，b是比奥系数，由多孔介质理论可以给出：

式中，Kb是材料的不排水体积模量，Km是矩阵体积模量，E是杨氏模量，v是泊松比。杨氏模量E通过函数E(ω)给出，说明比奥系数也受到孔隙扩展的影响。对于压实黏土，b可以直接取1。非饱和土中，基质吸力对压实粘土的力学性质及微裂纹的扩展有显著影响，因此需要将其影响考虑进来。如在土样失水干燥过程中，可以观察到干燥裂缝。这主要是由于土样固有的非均质性和结构上的影响。目前工作中只认为干燥裂缝是由于结构的影响。为此，在损伤演化中，要考虑到由于受限制的收缩变形而引起的局部张拉应力。提出了等效张拉应变的一个新形式ˆεeq，该形式将力学荷载和基质荷载引起的应变结合起来。由于基质荷载而引起的应变计算公式如下：

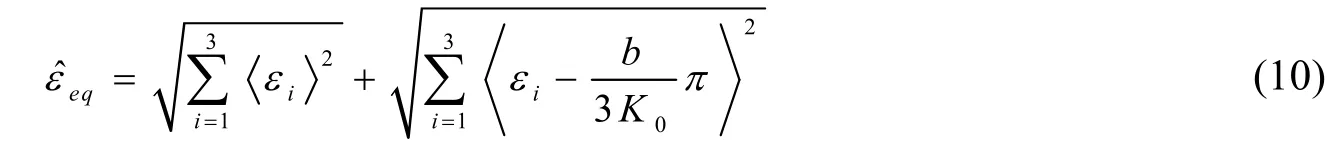
式第二项为基质吸力产生的等效拉应变。很明显，基质吸力引起的等效拉应变与等效孔隙压力π、比奥系数b、土体的体积模量K0有直接关系，取决于饱和度，因而ˆεeq受土样吸水饱和或失水干燥过程的控制。在等效应变的新形式中，式中的损伤驱动力是ˆεeq而不是εeq的函数。

1.1.4 模型参数的确定 在提出的压实黏土的力学模型中，有六个参数需要确定：两个未损伤材料的弹性参数(K0,G0)，及四个损伤特征参数(Bc，Bt，Yt0，Yc0)。参数确定方法如下：初始弹性常数，即初始体积模量K0和剪切模量G0，与初始杨氏模量E0和泊松比v0相关的，可从初始损伤前单轴张拉(或单轴压缩)试验应力应变曲线的线性部分获得。与张拉损伤有关的参数Bt和Yt0和与压缩损伤有关的参数Bc和Yc0，可分别通过拉伸和压缩试验确定。

1.2 压实黏土的裂缝本构模型

在压实黏土未形成宏观裂纹时，假定为均质，此时采用1.1中建立的黏土孔隙扩展模型。在图1中，应力达到峰值前，采用上述模型，这是典型的非线性过程。当孔隙发展到临界值，即图中标注的ω0时，应力也即将达到峰值，宏观裂缝出现。此时连续介质力学不再适用，需要将不连续体和宏观裂纹单独考虑。

在出现宏观裂纹的应力软化阶段需要引入软化曲线。以试验测量结果为依据，给出了一个经验公式如下：

式中，ft是材料的单轴抗拉强度，[un]m是对应应力为0的最大裂缝宽度，c1是模型参数，用来控制应力—裂纹宽度曲线的形状。实际中，由于裂纹展开而耗散的断裂能Gf可以直接通过峰后曲线来获得，如图2所示，其大小代表了曲线下的面积。上述三个参数表述了裂纹出现后的力学行为特征，可通过单轴张拉试验确定。

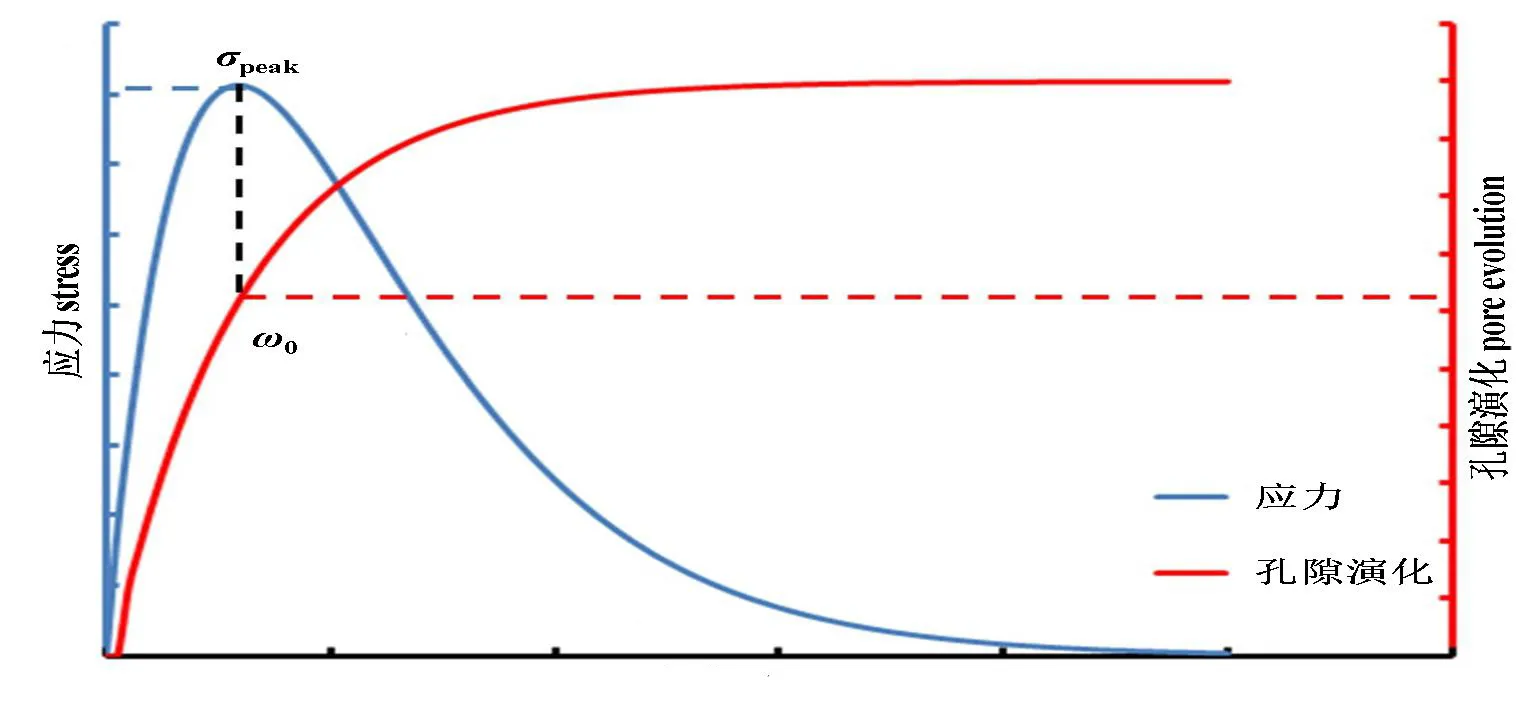
图1 岩土材料单轴拉伸应力应变全曲线及孔隙演化过程Fig.1 Complete stress-strain curve of geotechnical material under uniaxial tension and its pore evolution process

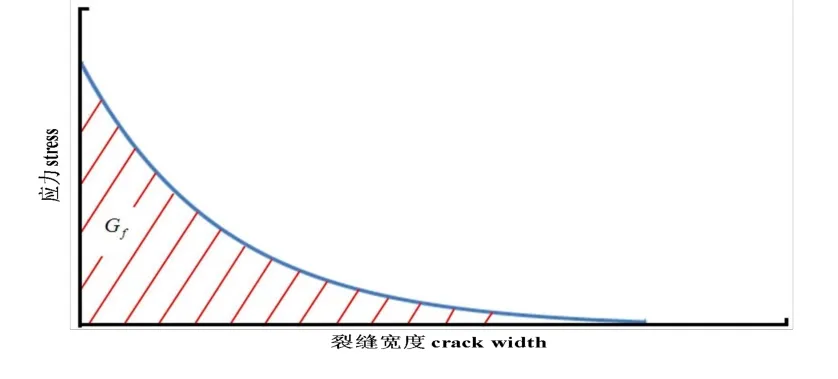
图2 岩土材料宏观裂缝的应力—裂缝宽度关系Fig.2 Relationship between stress and crack width of macroscopic crack of geotechnical material

连续介质力学和宏观裂隙的力学行为通过临界损伤值紧密地联系在一起，形成一个完整的分析，得到了连续的应力应变全曲线。如图3所示，在上升曲线部分，为连续介质力学的分析结果，下降曲线则是运用了裂缝张开模型分析的结果。

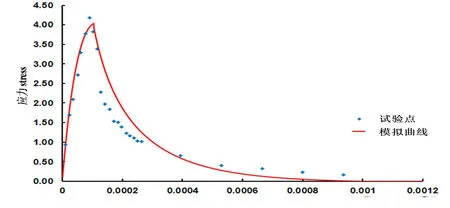
图3 岩土材料单轴拉伸试验曲线及其数值模拟Fig.3 Uniaxial tensile test curve of geotechnical material and its numerical simulation

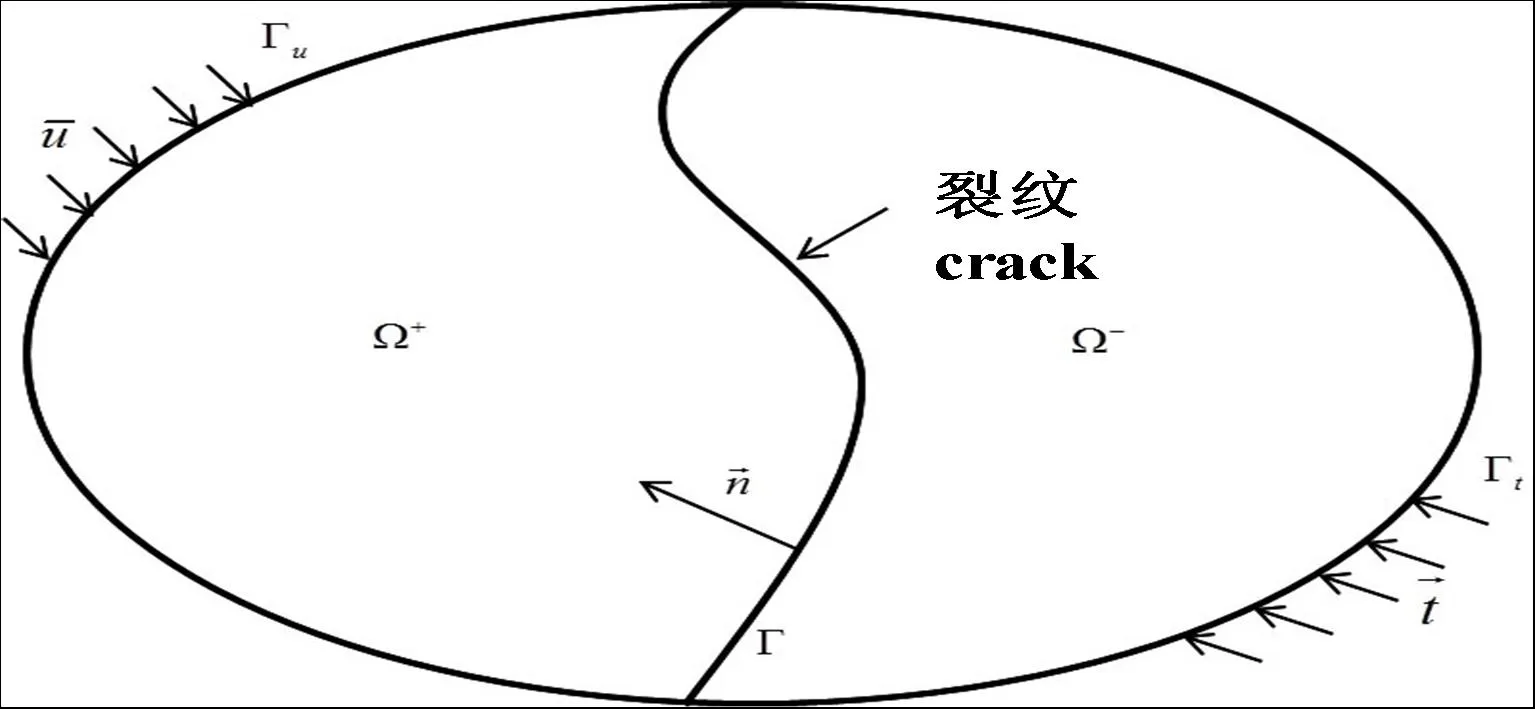
图4 带有裂纹的不连续体Fig.4 Discontinuity with crack

2 裂缝扩展数值方法

2.1XEFM方法

扩展有限元的基本观点是“扩展”被裂缝分割的单元节点自由度。“扩展”的自由度用来描述不连续体的“位移间断”。

2.1.1 XEFM位移模式 扩展有限元通过对裂缝分割单元结点增加额外自由度来表征不连续体，位移模式的一般形式：

式中Ω为带有裂纹的面积域(见图4)，Γ为裂纹，Ni为单元插值函数，ai为单元节点位移，Hj(x)为Heaviside函数，在裂纹面的上下两侧分别取值+1和-1，作为富集函数用以表示裂纹处位移的间断，

bi为“扩展”自由度的节点位移。式中第一项即为有限元的公式，而第二项为扩展自由度的贡献。

2.1.2 XEFM支配方程 利用虚功原理，建立扩展有限元法的支配方程：

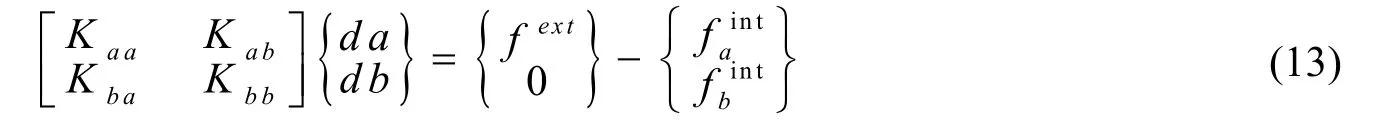
式中，da是常规有限元节点位移增量，db是扩展自由度的节点位移增量，为总体劲度矩阵，fext为外界施加在节点上的节点荷载，为由内力引起的常规自由度和扩展自由度的节点荷载列阵。实际上，上述支配方程可以简写为KU=F，这一表达和有限元法完全一致。

总体劲度矩阵由Kaa、Kab、Kba和Kbb四个单元劲度矩阵构成，其中与常规有限元单元劲度矩阵一致；考虑了常规和扩展自由度之间的耦合；描述了不连续体对劲度矩阵的贡献，其中T为裂缝的劲度矩阵，为下标n和t代表裂缝的法线和切线方向。

2.1.3 裂纹积分方法 被裂缝分割的单元，由于跳跃方程在整个方程区域内是不连续的，故在计算单元刚度矩阵和单元节点力时不像有限元法中那样进行Gauss积分，而是需要进行分区处理。被裂缝分割以后，分区则是不规则的四边形或三角形。为了解决这一问题，需将裂缝两边的区域全部离散为三角形。值得注意的是，这些三角形并不是新生成的单元，而是积分过程中使用的积分域，不形成额外的节点和单元。为了考虑裂缝对单元刚度矩阵和节点荷载的贡献，裂缝表面也进行了线积分。

2.2 裂缝扩展准则和扩展方向

关于黏土开裂，目前常用的准则主要有拉应力开裂准则和剪切开裂准则。拉应力开裂准则，即当土体中拉主应力达到土体抗拉强度时，土体开裂，裂缝的方向垂直于该拉主应力方向。该准则物理意义明确，但土石坝心墙内部通常都处于受压状态，并不存在拉应力。很多学者都认为心墙发生开裂是由于其满足拉应力开裂准则[13-15]，但即便存在“拱效应”，也很难使心墙的应力为零或负值[16]。剪切开裂准则即莫尔—库伦强度理论。在这里，还可以采用拉应变开裂准则，即当土中拉应变达到土体抗拉强度对应的拉应变时，土体开裂。相对于拉应力准则，对于心墙土体，拉应变准则更加适合，因为即便土体为压应力的条件下，拉应变也可能存在。

在本文计算中，极限拉应变、拉应力、抗剪强度、临界损伤同时作为裂缝开裂和扩展的准则。在每一个加载步后，那些没有被宏观裂纹分割的单元内的每个节点的损伤值都会被校核并和开裂准则比较。若开裂准则满足，那么有两种被区分的情况。第一种情况，若该单元在裂纹尖端范围内，这属于裂纹扩展情况。另一种情况，若该单元周围是普通的单元，那么在普通单元内会产生新的裂纹尖端。为了便于计算，允许裂纹扩展以确保尖端总在单元的边界上。同时，将富集函数添加到普通单元节点上以描述单元的位移间断。随着新裂纹的形成，在当前加载步下，整个结构的平衡会重新进行计算和校核，直到达到新的平衡。

裂缝扩展方向的确定是宏观裂纹扩展模型中最难解决的问题之一。在本文，采用了以平均张拉应力为基础的准则。宏观裂纹从它的尖端以垂直最大张拉应力的方向进行扩展。考虑到局部相互作用的影响，后期通过非局部平均应力张量来确定。

式中，w是Gauss型权函数，定义如下：

式中，r代表当前点和裂纹尖端之间的距离，lc是材料的特征长度，该特征长度决定了裂纹尖端周围相互作用域的范围。lc的数值取决于特征元的尺寸，在二维问题中，可以表示为：其中，Ae是二维网格中的平均单元面积。

3 数值模拟算例

工程背景为蒙阴县岸堤水库大坝，坝高29.80 m，顶宽7 m，为混凝土路面。主河槽坝段为粘土心墙砂壳坝。该坝修建于上世纪50年代末，当时建设标准偏低，施工质量较差。心墙局部土料含砂粒较高，渗透系数偏大，且土料整体压实不均匀，因而存在水力劈裂破坏的风险。

模拟试样为长20 cm高5 cm的长方形，其边界条件如图5所示。为了模拟土石坝心墙的边界条件，限制水平面前后方向的侧向变形，实际上就是一个平面应变问题，在试件的上部施加恒定的初始压力。在试件的左右两边水平位移全部限定，试件下部的竖向位移限定。试件的左边施加随时间变化的水压力，而试件右边水压力一直设定为0，试件的上部和下部皆为不透水条件。在试件中央设定一条预设的裂缝，其宽度为0.5 cm，长度为10 cm。库水压力的大小和变化可通过调整水压力的大小来模拟。

整个试件被划分1600个单元，1701个节点（图6），预设裂缝为蓝色区域部分，用于模拟土石坝中的软弱渗透面，竖向应力为0.5 MPa，左边的水压力在0.05 s内升高到0.2 MPa，然后保持这一水压力直到试验结束。土样力学参数通过三轴试验，并参考大坝试验报告相关成果综合确定，其中粘土的渗透系数为3.99×10-9m/s，砂土部分的渗透系数为1×10-3m/s。因为土样一直处于恒定压力状态下，采用开裂准则为拉应变准则。在裂缝扩展过程中，裂缝穿越单元的渗透系数也随之增加，采用和砂土一致的渗透系数。这是一个流固耦合加裂缝扩展的复杂过程。

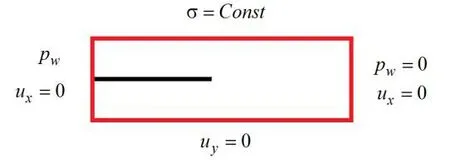
图5 水力劈裂模拟试件边界条件Fig.5 Boundary condition of hydraulic fracture simulation specimen

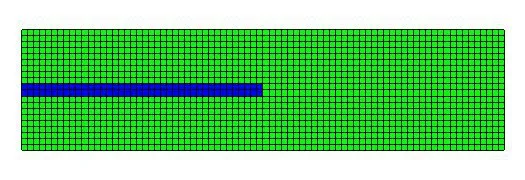
图6 试件网格划分Fig.6 Specimen mesh generation

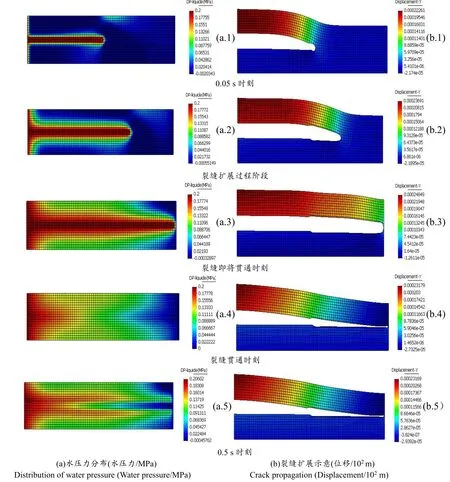
图7 试件不同阶段水压力分布及裂缝扩展示意图Fig.7 Distribution of hydraulic pressure and crack extension of specimen in different stages

图7 给出了对应于不同阶段的试件的水压力分布和变形网格竖向位移的分布。可以看出，在0.5 MPa的竖向压力下，在0.2 MPa的水压力冲击下，土样被劈裂。在0.05 s时，由于土样的渗透率较低，试件内部的水压力还基本保留为初始水压力。预设渗透弱面的渗透系数远远大于试件的渗透系数，其水压力在加压的同时达到了0.2 MPa。在这一水压力冲击下，预设的渗透弱面被水压力冲开，呈张开趋势，如图7(b.1)示意。使得裂缝前端的单元内部产生较大的拉应变，虽然在该时刻，试件仍然处于受压状态，但是预设裂缝的前部单元的拉应变已经达到了裂缝开裂准则规定的拉应变，裂缝开始扩展。

在裂缝扩展过程中，由于裂缝的张开，水压沿着裂缝向试件深部，即试件右边扩展，在水压力作用下，裂缝被撑开，使得裂缝前部单元一直处于拉伸状态，因此裂缝一直快速向前扩展，如图7(a.2)和(b.2)示意。在裂缝即将贯通时，裂缝被撑开达到最大程度。在裂缝贯通的一瞬间，由于试件右侧处于排水状态，裂缝中的水压力，特别是试件右边，水压力立即降到0。对应的裂缝同时闭合，随着时间的增加，裂缝中的水压力基本保持不变，相应的裂缝开度变化也不大。但是由于裂缝的扩展，土样与水的接触面加大，土样中的水压力很快达到稳定状态。

此算例虽然简单，但却验证了水力劈裂发生的两个基本条件，即“缺陷”和“快速蓄水的初期”[17,18]。缺陷即指心墙中应该存在薄弱面，算例中用渗透系数较大的单元来表示；而快速蓄水指需要一定的水力梯度，心墙内部的水压力本来很小，几乎为零，0.2 MPa的水头很快地进入到薄弱面中，才导致了裂缝的扩展，从而发生了水力劈裂。从图7中还可以看到，随着水力劈裂的发展，裂缝周围土样内部的孔隙水应力不断升高，即红色区域不断增大，这在一定程度上抵消裂缝和心墙的水头差，从而减缓裂缝扩展程度。当裂缝贯穿后，裂缝内的高水压力突然消失，裂缝闭合，土样内的水压力重新分布并达到稳定。正是由于水力劈裂后裂缝的快速闭合，才导致实际中的水力劈裂现象难以观察。算例不仅可以反映裂缝连续的扩展状态，还能反映裂缝周围孔隙水应力的连续变化，这是扩展有限元的优越性。

4 结论

本文建立了孔隙扩展模型和裂缝张开模型，并用扩展有限元法模拟水力劈裂过程，其模型参数可通过试验测得，且模拟过程严格服从热力学的不可逆定律。相比文献[4]，考虑了心墙中裂缝周围水压力随裂缝扩展过程的变化，也是一种进步。本方法对水力劈裂的数值研究提供了一种思路，但研究成果还有待室内试验和工程实例的验证。

[1]张丙印,于玉贞,张建民.高土石坝的若干关键技术问题[C].北京：中国土木工程学会第九届土力学及岩土工程学术会议,2003：163-186

[2]郭冲,邱秀梅,赵晓龙,等.土石坝心墙填土恒压吸湿变形试验研究[J].山东农业大学学报：自然科学版,2013,44(1)：76-80

[3]李全明,张丙印,于玉贞,等.土石坝水力劈裂发生过程的有限元数值模拟[J].岩土工程学报,2007,29(2)：212-217

[4]王俊杰,朱俊高.堆石坝心墙抗水力劈裂性能研究[J].岩石力学与工程学报,2007,26(增1)：2880-2886

[5]李录贤,王铁军.扩展有限元法XFEM及其应用[J].力学进展,2005,35(1)：5-20

[6]Belytschko T,Black T.Elastic crack growth in finite elements with minimal remeshing[J].International Journal for Numerical Methods in Engineering,1999,45：601-620

[7]Moës N,Dolbow J,Belytschko T.A finite element method for crack growth without remeshing[J].International Journal for Numerical Methods in Engineering,1999,46：131-150

[8]郭历伦,陈忠富,罗景润,等.扩展有限元方法及应用综述[J].力学季刊,2011,32(4)：612-625

[9]杜效鹄,段云岭,王光纶.重力坝断裂数值分析研究[J].水利学报,2005,36(9)：1035-1042

[10]方修君,金 峰,王进廷.基于扩展有限元法的Koyna重力坝地震开裂过程模拟[J].清华大学学报：自然科学版,2008,48(12)：2065-2069

[11]方修君,金 峰.裂隙水流与混凝土开裂相互作用的耦合模型[J].水利学报,2007,38(12)：1466-1474

[12]董玉文,任青文.重力坝水力劈裂分析的扩展有限元法[J].水利学报,2011,42(11)：1361-1367

[13]黄文熙.对土石坝科研工作的几点看法[J].水利水电技术,1982(4)：23-27

[14]孙亚平.水力劈裂机理研究[D].北京：清华大学,1985

[15]冯晓莹,徐泽平.心墙水力劈裂机理的离心模型试验研究[J].水利学报,2009,40(10)：1259-1263

[16]王俊杰,朱俊高,张 辉.关于土石坝心墙水力劈裂研究的一些思考[J].岩石力学与工程学报,2005,24(增2)：5664-5668

[17]朱俊高,王俊杰,张 辉.土石坝心墙水力劈裂机制研究[J].岩土力学,2007,28(3)：487-492

[18]赵晓龙,邱秀梅,韩慧敏,等.土石坝带裂缝黏土心墙破坏机理试验研究[J].中国农村水利水电,2016(2)：134-138