线性支出系统的试算分析法
2018-04-11宋子昀王伟玲
宋子昀,王伟玲
(1.广东水利电力职业技术学院 应用外语系,广州 510635;2.中山大学新华学院 生物医学工程学院,广州 510520)
0 引言
需求方程是研究市场消费品的需求重要工具,研究人们对各类商品的消费需求基本规律,从市场供给的角度探讨各种商品需求的影响因素,研究消费支出在各类商品之间的分配规律,探索消费结构。
线性支出系统是重要的消费结构研究模式,最为广泛的线性支出系统是英国经济学家斯通(Stone)于1954年提出的。线性支出系统的效用函数为:

相应的预算约束:

式中Z为预算总支出;
Pi为第i类商品的价格;
Xi为第i类商品的销售量。
按照效用最大化建立线性支出系统,见方程(3)。
线性支出系统:
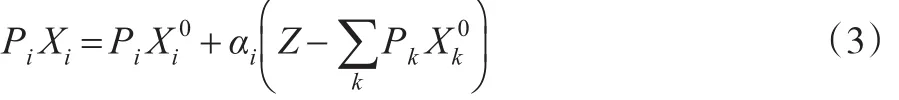
式中i=1、2、…、n;其余同上。

试算法:首先假设A并代入式(4),根据样本数据,采用OLS估计参数,再代入式(5):

检验假设值A是否正确。如果式(5)不满足,则重新假设A值,重复以上步骤,直至满足式(5),则假设的A值即为所求值,并代入式(3),即可直接估计其余参数。
单纯试算法的不足之处就是带有盲目性和不确定性,如果采用试算分析法可以克服这一缺点,使得线性支出系统的建立更加简便。
1 试算分析法
定义1:线性支出系统的试算模型为:
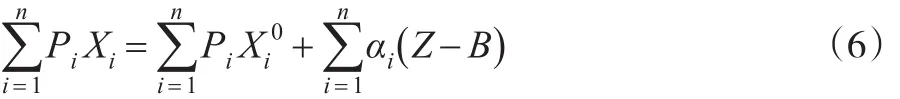
式中Z为预算总支出;
Pi为第i类商品的价格;
Xi为第i类商品的销售量。
αi,0<αi<1,∑αi=1;为非负常数,且可以看作第i类商品的最低需求量;
B为试算假定常数。
由式(5)和式(6)可以改写为:

定理1:线性支出系统的试算模型(7)中的ˆ和B为线性关系。
证明:将式(7)改写为:
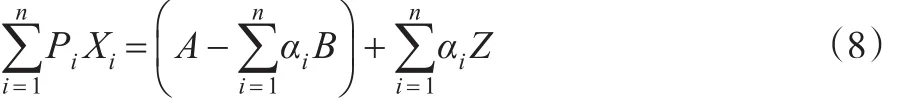

其中:

利用给定的样本数据,采用普通最小二乘法估计式(9),可以得到两个常数ˆ和ˆ,由式(10),得:

可以看出ˆ和B为线性关系,证毕。
定理2:如果B1、B2为B的两个假设值并代入下式:

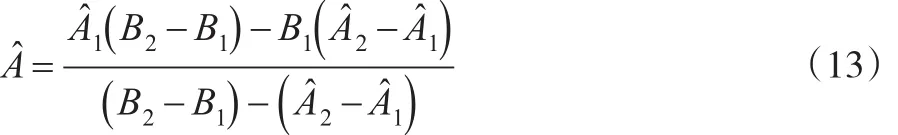
证明:设B1、B2为B的两个假设值,代入式(7),采用普通回归分析法分别估算,由于ˆ和B存在线性关系,则有插值公式:

式(14)中,当B=ˆ时,即为所要求的解,则有:

证毕。
根据定理2,可以估算A,将A代入式(3),并根据已知的Z和PiXi资料,可以直接估计其他参数(i=2、…、n):

由此建立线性支出系统模型。
2 算例
根据文献[1]提供的算例,有关商品消费数据见表1所示。

表1 有关商品消费统计表
估计线性支出系统的步骤如下:
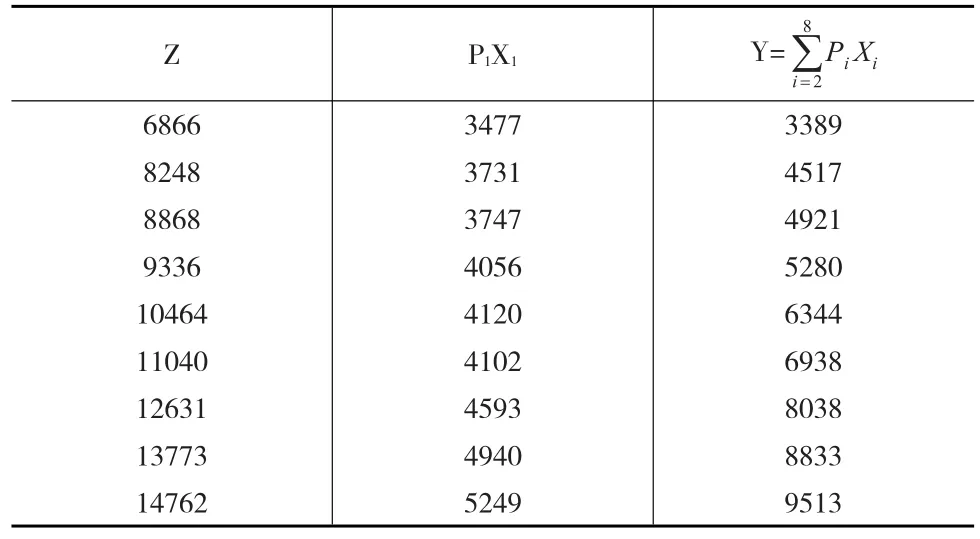
表2 变量合并后的商品消费统计表
假设 M1=10000和 M2=11000,代入方程(7)或方程(12),并根据表2数据,进行分别计算10979.9,由式(15)求得:。A=14140.6代入式(16)得:
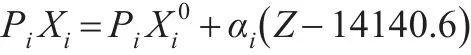
由此估算其余参数,结果见表3所示。

表3 各参数估计成果

与A的估计值Aˆ=14140.6基本相等。表3的参数估计成果代入式(3)即可得到线性支出系统预测方程。
3 结束语
线性支出系统和扩展线性支出是经济学的重要模型,系统所包含的因素众多,为建立线性支出系统和扩展线性支出系统模型,需要利用已知的Z和PiXi资料对众多参数进行估计,其计算量与变量数量有关,本文采用试算分析法,可以大大简便参数的估计工作量,可以快速、准确估算各参数,对经济分析提供有益的借鉴方法。
参考文献:
[1]李长风.经济计量学[M].上海:上海人民出版社,2010.
[2]汪潮阳,池峰.经济学基础[M].合肥:合肥工业大学出版社,2008.
[3][美]保罗·萨缪尔森,威廉·诺德豪斯.经济学[M].北京:人民邮电出版社,2011.
