基于灰色关联投影值的模糊物元评价法的改进

梁 瑛,季宪军

（南阳理工学院a.数学与统计学院；b.土木工程学院，河南 南阳 473000）

0 引言

模糊物元评价法在综合评价中已得到广泛应用，该方法能够将多个评价指标综合为一个总指标来进行评价，即根据待评样本与标准样本的“相近”的大小来进行优劣排序。

大部分学者利用该方法进行综合评价时，采用的是欧氏“贴近度”来度量待评样本与标准样本的接近程度。然而，用欧氏“贴近度”来描述待评样本与标准样本的“相近”的程度其实并不全面，因为它相当于仅考虑了待评样本与标准样本向量终点之间的距离，这样可能会导致多个待评样本的区分度不高。近几年又有学者结合灰色系统理论的灰色关联分析提出了灰色模糊物元分析法，灰色模糊物元分析法是采用“模糊关联度”来度量待评样本与标准样本的相近程度。模糊关联分析法是借鉴了灰色关联分析理论，利用模糊关联度仅是从几何曲线上考虑待评样本与标准样本的“相近”程度。本文结合灰色关联投影法，把模糊物元分析法中描述待评样本与标准样本的相近程度的欧氏“贴近度”进行改进，利用待评样本在标准样本上的投影值的大小进行综合评价。该方法把待评样本模的大小和待评样本与标准样本变化的一致性结合起来，全面地反应出了各待评样本与标准样本之间的接近程度，并通过实例验证了该方法的全面性和可靠性。

1 基于灰色关联投影值的模糊物元分析法

1.1 模糊物元

模糊物元是以“事物”、“特征”、“模糊量值”这三个要素组成的三元有序组作为描述事物的基本元。以R表示“模糊物元”，M表示“事物”，C表示“特征”，x表示与事物特征C相应的“模糊量值”，则有：

若事物M有n个特征，其相应模糊量值为，则此时形成n维模糊物元Rn。若事物共有m个：，且每个事物均有相同的n个特征，则形成m个事物的n维复合模糊物元Rmn。

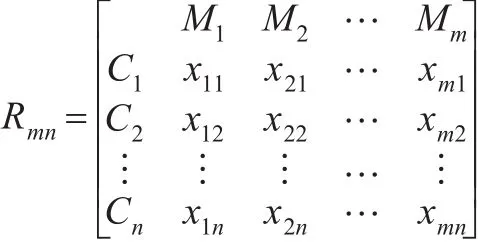
1.2 从优隶属度模糊物元

各评价指标相对于总体评价老说，有的评价指标是“效益型”指标（属性值越大越好型指标）；有的评价指标是“成本型”指标（属性值越小越好型指标）。

当评价指标Ci为“效益型”指标时，取x0i=mаx{x1i,x2i,…,xmi}即所有事物的第i个特征指标量值的最大值。当评价指标Ci为成本型指标时，取x0i=min{x1i,x2i,…,xmi}i=1,2,…,n，即所有事物的第i个特征指标量值的最小值。据此可得到标准的n维模糊物元，其中的模糊量值是所有事物的对应特征指标量值的最大值或最小值。

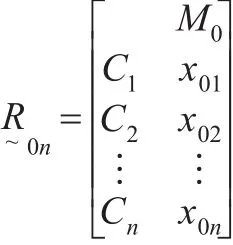
对指标进行比较时要具有统一的原则，这里采用从优隶属度原则，从优隶属度指各单项评价指标的模糊物元量值从属于标准方案中各对应评价指标的相应模糊物元量值隶属程度。指标从优的模式可采用以下方式。

当指标为效益型时：

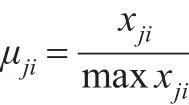
或

当指标为成本型时：

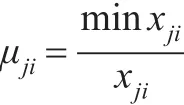
或

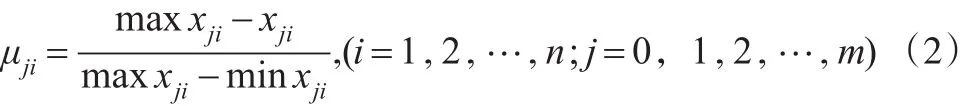
mаxxji,minxji为每一评价指标的最大值与最小值，无论采用那种形式均可得到从优隶属度模糊物元R～。

1.3 模糊物元投影值

由于各因素指标的相对重要性不同，因此各因素指标的权重也不同，权重确定的方法很多，总体上有主观权重法（AHP法、Delphi法、环比法等）、客观权重法（熵权法、变异系数法）和综合主客观权重的综合赋权法。如果第i个指标的权重为ωi，则n个特征的权重向量为W=(ω1,ω1,…,ωn)。则考虑权重的优化复合模糊物元记为RW，这里称为加权复合模糊物元，则有：

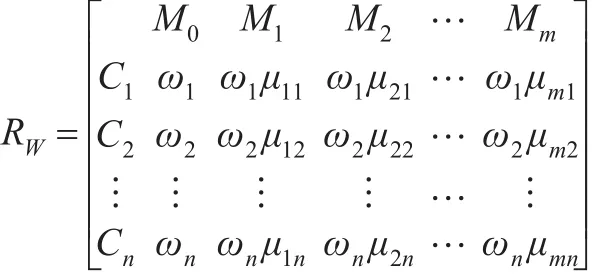
为了综合评价每一个模糊物元的优劣性，大部分文献采用欧氏距离作为关联函数，即用“欧氏贴近度”来描述待评样本与标准样本的贴近程度，所使用的欧氏贴近度为：

ρHj表示第j个待评样本与标准样本的贴近度，Δji（j=1,2,…,m;i=1,2,…,n）表示第j个n维模糊物元Mj与标准n维模糊物元相应分量差的平方，即Δji=

利用式（3）来描述待评样本与标准样本的“相近”程度显然不够全面。实际上每一个待评样本和标准样本为n维向量，从几何意义上来说式（3）相当于仅仅考虑两个加权复合模糊物元向量终点之间的距离（见图1）。

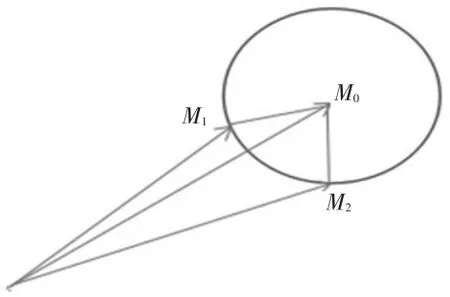
图1 欧氏贴近度几何示意图

从图1中可以看出，加权复合模糊物元M1、M2终点与标准模糊物元M0的终点距离相等，也就是它们与标准物元的“贴近度”相同，但显然它们与标准模糊物元的“相近”程度不一样。为全面考虑与标准物元的“相近”程度，结合灰色系统理论的关联投影法，可以通过模糊物元在标准模糊物元上的投影值来描述“相近”程度。由于关联系数与隶属度等价，因此可把最优隶属度直接作为关联系数，在RW中，将每个模糊物元看成一个列向量，则模糊物元Mj与标准模糊物元M0之间的夹角θj的余弦越大，表明模糊物元Mj与标准模糊物元M0之间的变化方向愈一致。将模的大小与夹角余弦的大小综合考虑，即考虑模糊物元Mj在标准模糊物元M0上的投影值就（见图2）可以全面准确的反应各个模糊物元Mj与标准模糊物元M0之间的接近程度。Mj在M0上的投影值为：

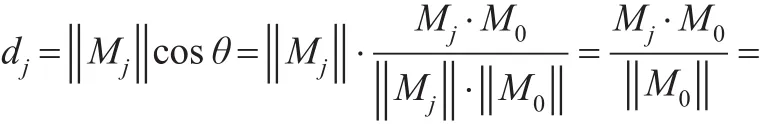
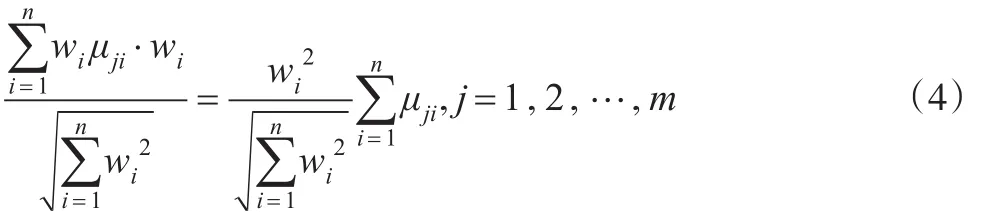
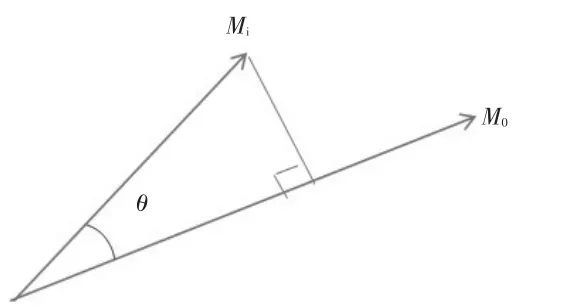
图2 Mj在标准模糊物元M0上的投影

基于灰色关联投影值的模糊物元分析法的计算步骤：

（1）构造m个事物的n维复合模糊物元Rmn；

（3）确定评价指标的权重，并计算投影权重；

（4）计算每一个待评样本在标准样本上的投影值；

（5）根据投影值的大小排序，确定最优方案。

2 实例

建筑企业总承包商在与多个分包商合作之后，为了确定以后是否可以再度合作，可以先建立对分包商的管理评价指标体系，然后总承包商对分包商的各项评价指标的满意程度进行打分，分值是介于0和1之间，分值越高表示总承包商对分包商的该项评价指标越满意，通过打分得到复合模糊物元。利用公式（1）和公式（2）计算出从优隶属度模糊物元

由于20项评价指标指标的重要性不一样，本文在AHP法确定的权重基础上，计算得到投影权重如表1所示，这里把最优隶属度直接看作关联系数。

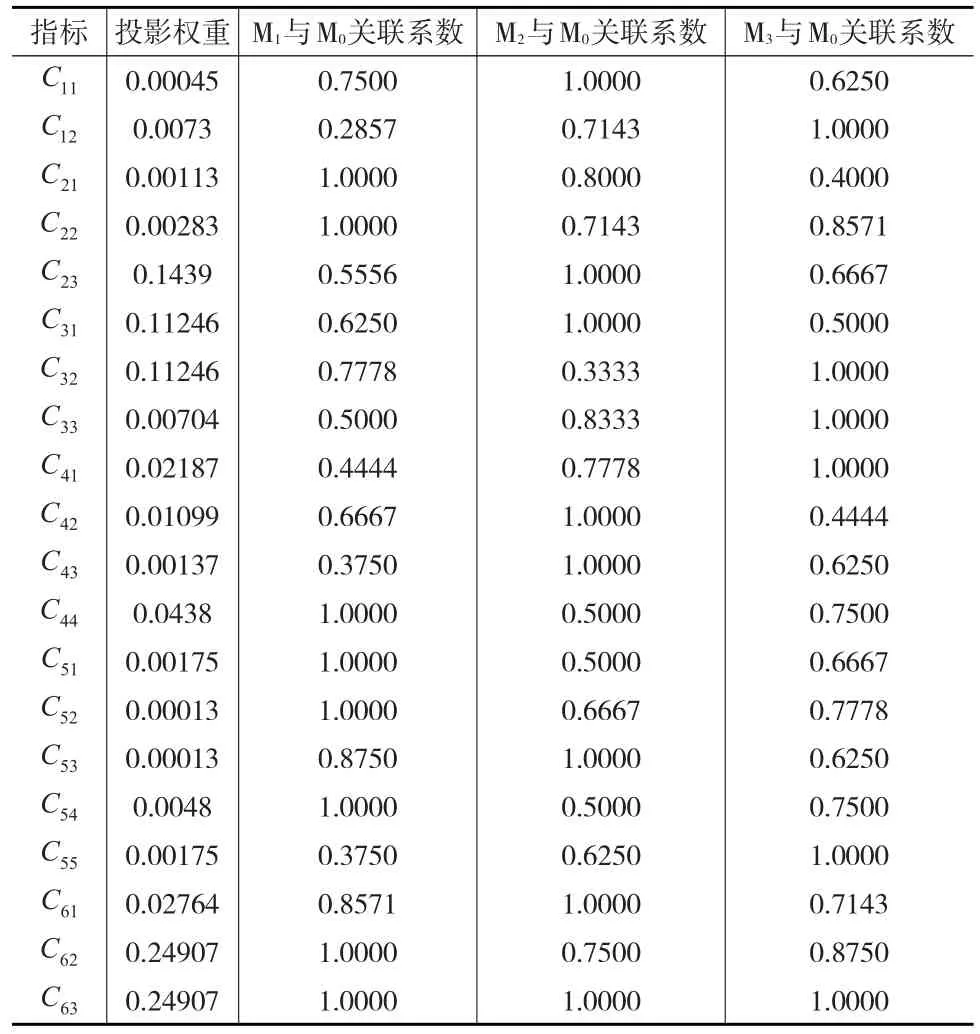
表1 指标的权重、关联系数

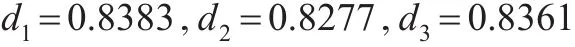
根据三个分包商的投影值可知，三个分包商的优劣次序为A≻C≻B，这与文献[4]所得的评价结果有所差异（评价对比见下页表2）。A公司虽然有4个指标的分数低于0.4，但他们所占的权重均比较小，而且A公司有8个指标的分数在三个公司中得最高分，其中包含权重最大的“目标的实现度”与“再次合作的意愿”两个指标。所以综合评价来说对A公司最为满意，其次是C公司，最后为B公司。

表2 两种方法评价对比表

3 结束语

本文结合灰色系统理论的灰色关联投影法，对模糊物元分析法中描述待评样本与标准样本的相近程度的欧氏“贴近度”进行改进，利用待评样本在标准样本上的投影值的大小进行综合评价。该方法把待评样本模的大小和待评样本与标准样本变化的一致性结合起来,全面反应出各待评样本与标准样本之间的接近程度，计算结果反映出评价的合理性，评价结果基本反映出真实情况。

参考文献：

[1]唐珍宝.基于PSR模型的福建省水资源可持续利用评价研究[J].环境科学与管理,2015，40(3).

[2]周泰，叶怀珍.基于模糊物元欧氏贴近度的区域物流能力量化模型[J].系统工程，2008,26(6).

[3]李雪峰.基于欧氏贴近度的模糊物元分析理论在桥梁健康等级评估中的应用[J].城市道桥与防洪，2011，(5).

[4]韩思颖，何亚伯.基于模糊物元的建筑企业分包商评价方法研究[J].数学的实践与认识，2015，45(22).

[5]王昌金,张永辉,黄彬.灰色模糊物元分析的要地防空威胁评估[J].火力与指挥控制，2013，38(8).

[6]高顺成.区域及中心城市居民购房压力的拟熵权模糊物元分析——综合分析区域城市、中心城市等17市[J].地域研究与开发，2010,29(6).

[7]王少勇，吴爱祥，韩斌等.自然崩落法矿岩可崩性模糊物元评价方法[J].岩土力学与工程学报，2014，33(6).

[8]张斌，雍歧东，肖芳淳.模糊物元分析[M].北京：石油工业出版社,1997.

[9]梁瑛,于育民.灰色关联投影法在助学金评价中的应用[J].南阳理工学院学报，2012,4(2).