空间薄膜天线索膜结构建模与形状优化

曹　鹏， 保　宏， 杜敬利， 彭福军

(1. 西安电子科技大学 电子装备结构设计教育部重点实验室，陕西 西安 710071;2. 上海宇航系统工程研究所，上海 201108)

在卫星通信、地球观测及深空探测等领域，可展开天线是必不可少的关键设备[1-2]．平面薄膜天线收纳比大、质量轻、加工成本低，是空间天线结构的研究热点之一．其中，天线精度是结构设计的重要指标，而薄膜边界形状对膜面应力分布及膜面精度有着重要影响[3]，已成为平面薄膜天线的重要研究内容．

由于平面薄膜天线在边界处存在索膜滑移现象，所以建模时不容忽略．文献[4]在对一种新型薄膜材料进行张拉分析时，将边界处张拉带与薄膜采用相同单元划分并共享节点，该方法使边界变形更加协调，但实际是对边界进行简化处理，并未解决滑移问题．文献[5]基于索膜滑移过程中节点索力连续及全局索力平衡关系建立了滑移索单元与滑移膜单元，但仅得到静力平衡结果，无法模拟索段滑移的运动过程．文献[6]采用动力松弛法建立了一种滑移索单元，但未考虑索膜间的摩擦力因素．文献[7]将连续索离散成质点集合，并基于质点运动的牛顿第二定律，推导了滑移索单元的内力公式．文献[8]根据滑移索拉力与长度之比的变化推导了索段的滑移刚度．但上述研究着重考虑索段与支点之间的切点变化，未考虑索段与支点的滑移稳定问题．

针对薄膜边界形状如何确定的问题，学者主要研究了抛物线、圆弧及椭圆等特定形状．文献[9]对圆弧边界薄膜施加双轴等值拉力，发现膜面应力分布较为理想，可有效避免褶皱产生．文献[10]认为当膜面处于双轴等值应力状态时，褶皱出现的可能性最小，并基于张力场理论证明了薄膜在双轴等值应力状态下形成的边界曲线为圆弧．文献[11]分别对薄膜施加一定张拉力及热载荷进行实验，发现薄膜边界褶皱区域近似为椭圆，因此认为将椭圆形褶皱区域裁剪掉，便可得到理想薄膜边界．类似地，文献[12]也通过大量张拉实验总结出薄膜边界褶皱区域裁剪曲线的经验公式．但上述研究主观性较强，缺少理论证明，难以应用到实际工程中．文献[13]采用椭圆曲线建立薄膜初始边界，通过对应力集中区的曲线进行修正来减少膜面变形．文献[14]中针对圆弧形边界薄膜分析了在一定压力条件下，薄膜的固有频率与边界几何参数之间的关系，认为当边界形状致使薄膜面积减少时，薄膜的固有频率增加．

目前对薄膜边界形状的研究存在两点不足: 首先，内悬索与薄膜在建模时按理想化处理，将边界处索元与膜元共享节点，简化误差较大; 其次，对薄膜边界形状的研究均针对特定形状展开，如抛物线、圆弧、椭圆等，具有很大的局限性，且当特定形状薄膜受张拉后，边界发生变形，与预设形状不一致，将对结构分析带来一定误差．针对以上问题，笔者考虑了索膜在受张拉时产生滑动的情况，建立了一种非线性有限元模型，并在此基础上，将索膜边界视为B样条曲线，以曲线控制点位移为设计变量，通过优化索膜结构实际应力与工程参考应力间的偏差，实现了对薄膜在任意初始边界下的形状优化，科学、合理地确定了边界形状．

1　平面薄膜天线索膜结构边界建模

图1　平面薄膜天线结构示意图

平面薄膜天线结构如图1所示，薄膜通过牵连索及内悬索张拉于周边刚架上; 内悬索与薄膜的连接方式以及边界形状等因素会直接影响悬索与薄膜间的应力传递，进而影响膜面精度．在实际中，为实现悬索对膜面的均匀张拉，内悬索会置于乳胶管中，当内悬索受张力作用时将与薄膜产生相对滑动．传统的有限元建模将边界处索元与膜元共享节点，忽略了索膜间的滑动作用，这将对结构分析等带来一定误差．

悬索与薄膜间相对滑动是应力平衡的过程．在滑动作用下，索膜应力集中程度降低，膜面应力分布将更加均匀，这一过程与弹簧的作用类似，因此笔者采用弹簧单元建立内悬索与薄膜边界的连接关系．在进行结构有限元建模时，边界处索节点与膜节点处于同一位置，在悬索与薄膜重合节点之间建立两个零长度的面内单自由度弹簧单元．设薄膜法向为z，则两弹簧单元分别在x及y向承受拉伸作用，弹簧单元的面内形变可模拟索膜间的相对滑动．

2　平面薄膜天线边界形状优化

样条曲线是由一组控制点插值或逼近得到的光滑曲线，其中B样条曲线定义如下:

(1)

其中，Pi为曲线控制点，Ft，n(t)为n次B样条基函数，其形式为

(2)

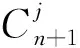
B样条曲线采用分段定义．若给定m+n+1个顶点Pi(i=0，1，2，…，m+n)，则可定义m+1 段n次B样条曲线，且曲线在顶点处n-1 阶连续．与其他样条曲线相比，B样条曲线更加灵活，局部形状受顶点控制更加明显，具有良好的局部修改能力和较好的逼近性能．基于此，采用B样条曲线建立薄膜边界并进行形状优化，计算模型如图2所示．

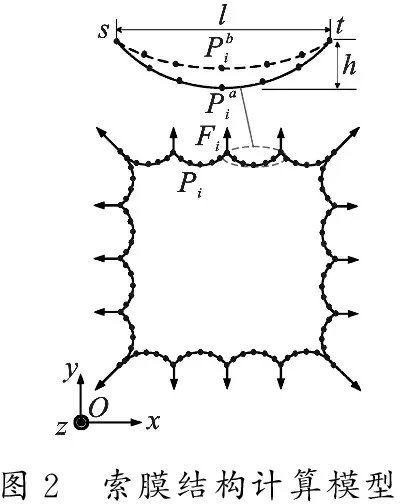
图2 索膜结构计算模型

天线结构优化通常以精度或质量作为优化目标，而薄膜抗弯刚度小，易屈曲，应力分布会严重影响膜面刚度及精度．一般来说，膜面应力越大，抗变形能力越强．然而，一味寻求较大的应力必然会降低材料的使用寿命．经综合考虑，膜面应力应尽可能地接近工程期望的参考应力状态．因此，笔者以图2所示曲线控制点Pi(i=1，2，…，N)的位移为设计变量，通过最小化结构实际应力与工程参考应力间的偏差来寻求最优边界形状．

假设薄膜边界由L段B样条曲线组成，每段曲线取M个控制点，每个控制点赋予两个面内自由度，则边界形状优化的设计变量数N为2LM，曲线形状变化如图2中局部放大图所示，曲线垂跨比μ=h/l．设薄膜共划分为n个单元，内悬索共划分为m个单元，牵连索张拉力为Fi(i=1，2，…，L)．约束条件如下:薄膜应力不超过材料容许应力[σ]mem；悬索应力不超过材料容许应力[σ]cab;结构基频不低于给定值f0；控制点位移最小值为Pl;控制点位移最大值为Pu．

优化模型如下:

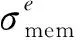
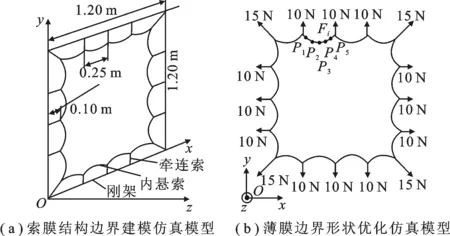
图3　仿真校验模型示意图

3　仿真校验

通过如下算例对笔者提出的索膜结构边界建模及形状优化方法进行仿真校验．

3.1　索膜结构边界建模仿真算例

采用弹簧单元模拟索膜结构边界处的滑动现象，并基于图3(a)所示模型进行了数值仿真．材料参数如表1所示．悬索通过初应变施加预张力并使膜面产生一定预应力．为对比弹簧单元建模法与共享节点建模法的区别，模拟了膜面在空间受一定光压的工况进行分析．在实际中，太空光压约为 9× 10-6Pa，数值较小．为方便分析对比，对膜面施加 1 Pa 的法向压力．研究表明，薄膜屈曲变形主要由第2主应力决定，故此处提取膜面第2主应力进行对比．经多次求解发现，当弹簧刚度系数k取值位于[0， 2× 107N/m] 范围内时，随刚度系数的增大，弹簧单元法计算结果与共享节点法计算结果越接近，直至相等．为有效模拟索膜间的滑移作用，弹簧刚度系数取值不宜过大，此处取 2× 103N/m．其中，薄膜应力数值如表2所示，薄膜应力分布如图4所示．

由表2可知，与共享节点建模法相比，建立弹簧单元后膜面第2主应力平均值、最大值及均方根值均减小，说明膜面应力分布更均匀，应力集中程度降低．由图4可知，建立弹簧单元后，薄膜第2主应力分布形式和应力梯度发生了明显变化，由云图与数值同样可看出结构应力集中程度降低．在实际中，悬索与薄膜相对滑动是应力平衡的过程．在滑动作用下，索膜应力集中程度将降低，膜面应力分布将更均匀．数值模拟结果与实际规律一致，说明弹簧单元可有效地模拟索膜滑动的效果．该方法将使薄膜天线索膜边界建模与结构分析更加准确．

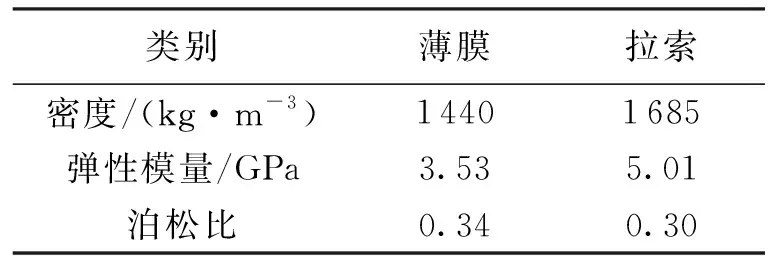
表1　材料参数

表2薄膜第2主应力静力分析结果MPa

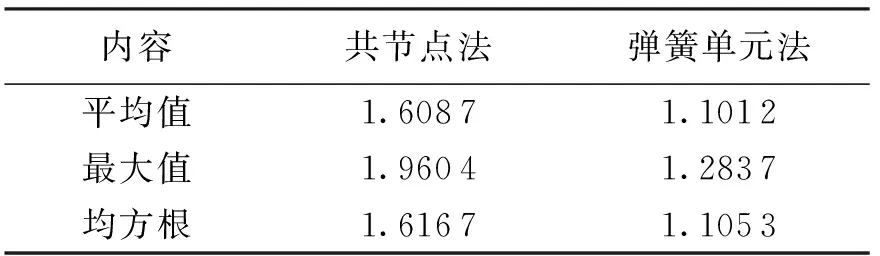
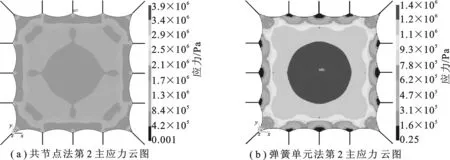
图4　薄膜第2主应力云图

3.2　薄膜边界形状优化算例

以如图3(b)所示模型为例对优化方法进行校验．该模型边界由16段B样条曲线组成，每段曲线取7个控制点．为保证结构对称性并减小计算量，首先将16段样条曲线相同位置的控制点Pi(i=1，2，…，N)归并为一类，并将每段曲线两端固定，中间5个控制点按对称性归并为3类，则该优化问题最终有3个设计变量，分别为P1、P2和P3．以弦长为 25 cm、圆心角为60°的圆弧为基准建立曲线的初始边界，则初始形状的垂跨比μ为0.134．以初始位置为基准，当控制点沿径向远离薄膜对称中心移动时，位移为负，反之为正．

设定控制点P1的位移范围为[-15 mm，10 mm]，P2为[-15 mm，10 mm]，P3为 [-22 mm，22 mm]．薄膜工程参考应力值为 1.315 MPa，内悬索工程参考应力值为 2.581 MPa，结构基频不低于 0.062 Hz．尼龙拉索直径为 1.4 mm，容许应力为 1 670 MPa；聚酰亚胺薄膜厚度为 0.025 mm，容许应力为 231 MPa．牵连索张力大小如图3(b)所示．调用Matlab软件中的fmincon库函数进行优化，优化结果如表3所示．薄膜初始形状及优化形状对比如图5所示．

表3　优化结果

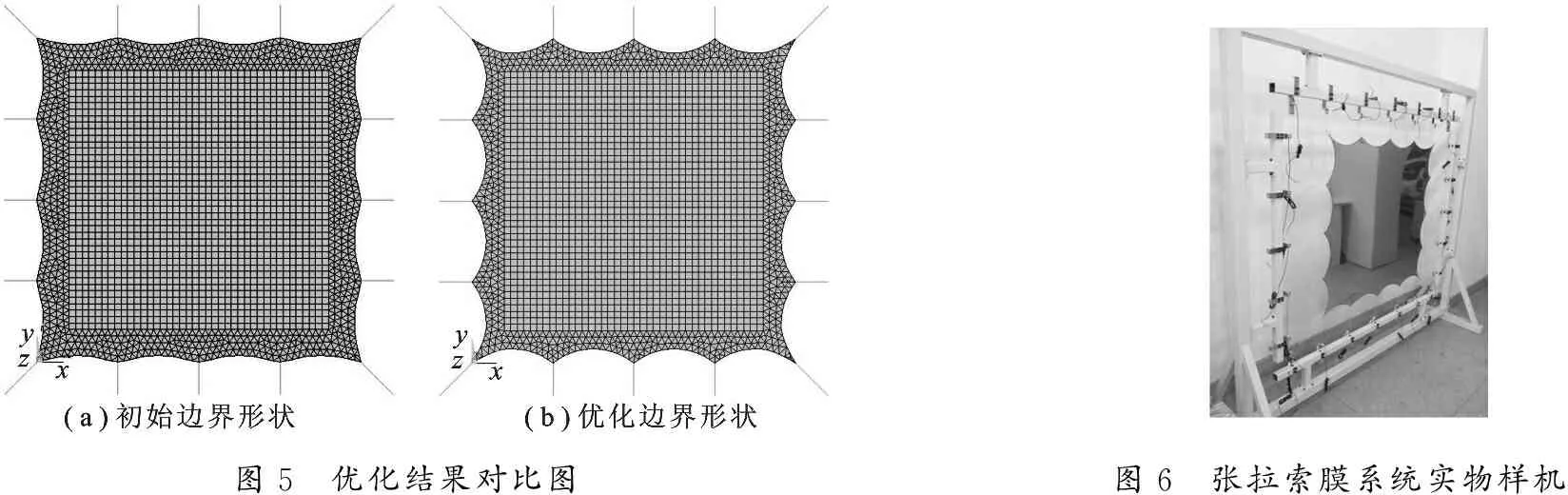
图5 优化结果对比图图6 张拉索膜系统实物样机

由表3可知，经过优化，目标函数值即索膜结构单元应力偏差由 0.895 MPa 降低到 0.646 MPa，降幅为27.8%；曲线垂跨比由0.134变为0.176，结构基频有一定提高．由图5可知，优化形状合理性强，符合工程中的一般规律，优化结果验证了笔者提出方法的有效性．

4　实验验证

为检验优化结果的可靠性，根据图3(a)所示尺寸制作了图6所示张拉索膜系统样机，并以优化形状裁剪薄膜进行张拉实验．薄膜由悬索张拉于周边刚架上，悬索张力由拉力传感器测量．对悬索施加图3(b)所示的张力后，采用摄影测量技术获得膜面变形的均方根误差．经测量，膜面均方根误差为 0.13 mm，精度较高，形状优化取得了良好的效果．由于硬件限制，膜面应力暂无法测量，完善的实验研究将在后期继续进行．

5　总　　结

针对平面薄膜天线边界处悬索与薄膜存在滑动的特点，建立了一种考虑索膜滑动的非线性有限元模型，并通过数值模拟说明了该方法的有效性．笔者提出的方法将使平面索膜结构的建模与分析更加准确．

基于非线性有限元模型，将薄膜边界视为B样条曲线，通过优化曲线控制点位移得到最优边界形状，并通过数值仿真和实验测量对该方法进行了验证．该优化方法突破了特定边界形状的局限性，科学、合理地确定了最优边界形状．此外，通过优化，膜面应力分布更接近工程期望值，使得膜面刚度更加合理，将有助于提高材料使用寿命并降低膜面变形率．该方法为薄膜边界形状设计提供了一定的参考．

参考文献：

[1] 李团结, 张琰, 段宝岩. 周边桁架可展开天线展开过程运动分析及控制[J]. 西安电子科技大学学报, 2007, 34(6): 916-921.

LI Tuanjie, ZHANG Yan, DUAN Baoyan. Motion Analysis and Control of Deployable Truss Antenna[J]. Journal of Xidian University, 2007, 34(6): 916-921.

[2]刘帅杰, 段宝岩, 杨东武. 利用区间与概率的星载可展天线齿轮防卡分析[J]. 西安电子科技大学学报, 2016, 43(3): 61-66.

LIU Shuaijie, DUAN Baoyan, YANG Dongwu. Interval and Probability Based Analysis of Seizure-preventing for Synchronous Gears of the Astromesh Deployable Satellite Antenna[J]. Journal of Xidian University, 2016, 43(3): 61-66.

[3]WANG C G, XIA Z M, TAN H F. Initial Shape Design and Stability Analysis of Rib for Inflatable Deployable Reflector[J]. AIAA Journal, 2015, 53(2): 486-492.

[4]DINH T D, REZAEI A, PUYSTIENS S, et al. A Study of Tension Fabric Membrane Structures under in-plane Loading: Nonlinear Finite Element Analysis and Validation[J]. Composite Structures, 2015, 128: 10-20.

[5]PARGANA J B, LLOYD-SMITH D, IZZUDDIN B A. Fully Integrated Design and Analysis of Tensioned Fabric Structures: Finite Elements and Case Studies[J]. Engineering Structures, 2010, 32(4): 1054-1068.

[6]PAULETTI R A O, GUIRARDI D M, GOUVEIA S. Modeling Sliding Cables and Geodesic Lines through Dynamic Relaxation[C]//Proceedings of the 2009 International Association for Shell and Spatial Structures(IASS) Symposium, Valencia Evolution and Trends in Design, Analysis and Construction of Shell and Spatial Structures. Madrid: IASS, 2009: 2047-2058.

[7]俞锋, 罗尧治. 索杆结构中索滑移行为分析的有限质点法[J]. 工程力学, 2015, 32(6): 109-116.

YU Feng, LUO Yaozhi. The Finite Particle Method for Analysing Cable Sliding in Cable-strut Structures[J]. Engineering Mechanics, 2015, 32(6): 109-116.

[8]蔡建国, 冯健, 汪凯. 考虑拉索滑移的索杆结构展开过程模拟[J]. 预应力技术, 2015(6): 16-21.

CAI Jianguo, FENG Jian, WANG Kai. Simulation of Cable-strut Structure Expansion Considering Cable Sliding[J]. Prestressing Technology, 2015(6): 16-21.

[9] HEALD J C, POTVIN M J, JIANG X X. Experimental Investigations to Support a Multi-layer Deployable Membrane Structure for Space Antennae[C]//Proceedings of the 2005 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, , 2005: 6302-6312.

[10]汪有伟, 关富玲, 韩克良. 内外部悬索联合张拉膜结构的设计与分析[J]. 浙江大学学报: 工学版, 2010, 44(6): 1213-1219.

WANG Youwei, GUAN Fuling, HAN Keliang. Design and Analysis of Inner and Outer Cables Suspended Membrane Structure[J]. Journal of Zhejiang University: Engineering Science Edition, 2010, 44(6): 1213-1219.

[11]WANG X Y, SULIK C, ZHENG W P. High-fidelity Wrinkling Analysis of Membrane Structures and Elliptical Cut Optimization[C]//Proceedings of the 2008 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2008: 2008-2255.

[12]BONIN A S, SEFFEN K A. De-wrinkling of Pre-tensioned Membranes[J]. International Journal of Solids and Structures, 2014, 51(19/20): 3303-3313.

[13]ORSZULIK R R, SHAN J. A Simple PI Controller for Active Flatness and Tracking Control of a Space Membrane Structure[C]//Proceedings of the 2012 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2012: 98132.

[14]刘充, 李玉宇, 保宏, 等. 边界几何参数对空间平面张拉膜结构固有频率影响研究[J]. 振动与冲击, 2015(20): 198-202.

LIU Chong, LI Yuyu, BAO Hong, et al. Natural Frequencies of Pre-tensioned Membrane Structure with Different Boundary Geometrical Parameters[J]. Journal of Vibration and Shock, 2015(20): 198-202.