解非单调变分不等式投影算法的扰动分析

唐南春，叶明露

(西华师范大学 数学与信息学院，四川 南充　637009)

常见的求解变分不等式的数值算法有投影算法、牛顿算法、邻近点算法等，见参考文献[1-3]及其引用文献。其中投影算法因为易于实施的特点得到了广泛的关注。为了求解不同的凸优化问题，变分不等式的算法也不同，可参考文献[1,4-9]。

文献[10]介绍了一种二次投影算法来解伪单调非Lipschitz连续变分不等式问题。该算法的下一迭代点是通过向可行集与一个半空间的交的投影来实施。但在使用MATLAB计算投影时可能会因为精度问题而产生误差(特别是投影不易计算时)。因此，文献[11]给出该算法在扰动情形下的收敛性分析。

2015年Ye和He在文献[12]中介绍了求解非单调的变分不等式投影算法。该算法的第k+1个迭代点由第k个迭代点向可行集与前k个半空间的交的投影来实施。因此，随着k的增加，投影计算也越来越复杂。因此，有必要对该算法的新的迭代点的生成做一个扰动分析。

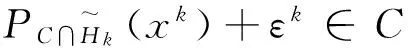
1　算法和预备知识

考虑的变分不等式问题VI(C,F)是指:寻找一个点x*∈C, 使得

〈F(x*),y-x*〉≥0,∀y∈C。

(1)

其中C⊆Rn,C非空的闭凸集，F∶Rn→Rn是一个连续映射，‖·‖ 和〈·,·〉分别为Rn中通常的范数和内积。

设VI(C,F)的解集为S，其对偶变分不等式的解集记为SD，即：

(2)

本文总假设SD≠∅和F在Rn上连续，又因为C是凸集，则有

SD⊂S。

(3)

记x到C上的投影定义为PC(x)∶=argmin{‖y-x‖|y∈C}。记x到C上的距离为d(x,C)∶=inf{‖y-x‖|y∈C}。注意到C是Rn中的闭凸集，从而有d(x,C)∶=‖x-PC(x)‖。记自然残差映射r(x)∶=x-PC(x-F(x))。

算法1选取初始点x0∈C，和参数σ∈(0,1),γ∈(0,1),k从0开始取。

第一步计算r(xk),如果r(xk)=0，那么停止，否则执行第二步。

第二步找出满足下列式子的最小非负整数m并令其为mk，

〈F(xk)-F(xk-γmr(xk)),r(xk)〉≤σ‖r(xk)‖2。

(4)

令ηk=γmk,zk=xk-ηkr(xk)。

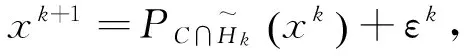
(5)

令k=k+1，再回到第一步。

注2算法1的第二步是合理的，如果‖r(xk)‖=0，则xk是(1)的解，此时程序停止，若‖r(xk)‖≠0，若{xk}是算法生成的无穷的序列，我们总有‖r(xk)‖>0。

下面我们说明算法的线搜索(即第二步)是合理的，假设对任意的非负整数m都不满足(4)式，即

〈F(xk)-F(xk-γmr(xk)),r(xk)〉>σ‖r(xk)‖2。

因为γ∈(0,1)，F连续，随着m趋近于，F(xk)-F(xk-γmr(xk))收敛到0，那么〈F(xk)-F(xk-γmr(xk)),r(x)〉也趋于0。从而有0≥σ‖r(xk)‖2>0。得到矛盾，故总存在一个非负整数mk使得(4)式成立。

引理1[4]若C是Rn中的非空闭凸集且x∈Rn，则有以下结论成立

(i)z=PC(x)⟺〈z-x,y-z〉≥0,∀y∈C;

(ii)〈PC(x)-PC(y),x-y〉≥0,∀x,y∈Rn;

(iii)‖PC(x)-PC(y)‖‖x-y‖,∀x,y∈Rn;

(iv)‖PC(x)-z‖2‖x-z‖2-‖PC(x)-x‖2,∀x∈Rn,∀z∈C。

引理2[4]若x*∈S，当且仅当‖r(x*)‖=0。

引理3[8]对∀x∈C,有

〈F(x),r(x)〉≥‖r(x)‖2。

(6)

引理4[8]设C是Rn中的闭凸集，h是Rn上的实值函数，K∶={x∈C∶h(x)≤0}。如果K≠∅,h在C上Lipschitz连续，其Lipschitz系数为L(即：∀x,y∈C,‖h(x)-h(y)‖≤L‖x-y‖)，则有

d(x,K)≥L-1max{h(x),0},∀x∈C。

为了阅读的方便，我们列其证明如下：

证明(i)当x∈K时，d(x,K)=0,h(x)≤0，故d(x,K)≥L-1max{h(x),0}成立。

(ii)当x∈CK时，因为K是闭集(h在C上连续，C为闭集),所以存在y(x)∈K,满足‖x-y(x)‖=d(x,K),由h的Lipschitz连续性有

‖h(x)-h(y(x))‖≤L‖x-y(x)‖=Ld(x,K)。

因为x∉K,y(x)∈K,则h(x)>0,h(y(x))≤0。所以

h(x)≤h(x)-h(y(x))=|h(x)-h(y(x))|≤Ld(x,K)

。

结论得证。

ai+1≤ai+δi,∀i≥i0。

(7)

那么{ai}收敛。

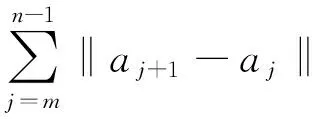
引理6{xk}是由算法1产生的序列，则有以下的结论：

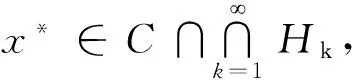
(8)

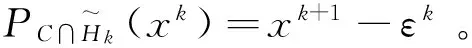
‖xk+1-εk-x*‖≤‖xk-x*‖。

从而由范数的性质有：

‖xk+1-x*‖-‖εk‖≤‖xk-x*‖。

所以

‖xk+1-x*‖≤‖xk-x*‖+‖εk‖。

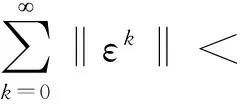
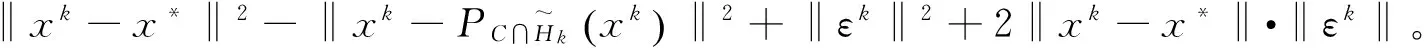
所以有

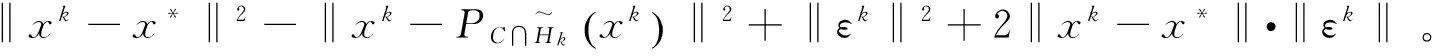
(9)

(9)式可等价地写为

(10)

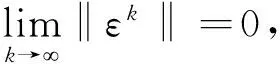
引理7设函数hk通过(5)式定义，{xk}是由算法1产生的无穷序列，如果SD≠∅，

(i)对任意的k，有

hk(xk)≥(1-σ)ηk‖r(xk)‖2>0。

(11)

(ii)如果x*∈SD,对任意的k，有

hk(x*)≤0。

证明(i)zk=xk-ηkr(xk)，由算法1里的(5)式hk的定义，有

hk(xk)=〈F(zk),xk-zk〉=〈F(xk-ηkr(xk)),ηkr(xk)〉

=ηk〈F(xk-ηkr(xk)),r(xk)〉

=ηk〈F(xk-ηkr(xk))-F(xk)+F(xk),r(xk)〉

=ηk[〈F(xk-ηkr(xk))-F(xk),r(xk)〉+〈F(xk),r(xk)〉]

≥ηk[-σ‖r(xk)‖2+〈F(xk),r(xk)〉]

≥ηk(1-σ)‖r(xk)‖2>0。

其中第一个不等式由线搜索(4)式可得，第二个不等式由引理3的(6)式可得。

(ii)由(5)式hk的定义有：

hk(x*)=〈F(zk),x*-zk〉。

又因为xk∈C且C是凸集，所以有zk∈C。从而由(2)式及x*∈SD,可得：

〈F(zk),x*-zk〉≤0。

那么对任意的k，都有hk(x*)≤0。

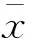
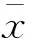
2　算法的收敛性

定理2.1如果F在C上连续且SD≠∅且{xk}为算法1生成的序列，则要么算法1在有限步终止(此时停止点为变分不等式的解)；要么{xk}收敛到 问题(1)的解。

证明因为{xk}有界，且F(x)和r(x)在Rn上连续，所以{zk}有界，再由F的连续性，可得{F(zk)}是有界序列，设此界为M>0,即：

‖F(zk)‖≤M,∀k。

则对任意k,M均为函数hk(v)在Rn上的Lipschitz常数，由引理4知

d(x,C∩Hk)≥M-1max{hk(x),0},∀k,∀x∈C。

再结合(11)式，有

d(xk,C∩Hk)≥M-1hk(xk)≥M-1(1-σ)ηk‖r(xk)‖2。

(12)

又由引理6里的(ii)有：

(13)

(14)

由(13)和(14)式，显然有

(15)

再联立(13)和(15)，从而有

(16)

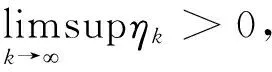
〈F(xkj)-F(xkj-γ-1ηkjr(xkj)),r(xkj)〉>σ‖r(xkj)‖2。

(17)

又因为F(x)和r(x)都是连续的，并且序列{xk}有界，当j→时，(17)式左边极限趋于0，有

(18)

参考文献：

[1]SOLODOV M V,SVAITER B F.A new projection method for variational inequality problems[J].SIAM Joural on Contral and Optimization,1999,37(3):765-776.

[2]MARCOTTE P,DUSSAULT J P.A modified newton method for solving variational inequalities[C]//Decision and Control,IEEE Conference on.IEEE Xplore,1985:1433-1436.

[3]BURACHIK R S,IUSEM A N.A generalized proximal point algorithm for the variational inequality problem in a Hilbert space[J].SIAM Journal on Optimization,2006,8(1):197-216.

[4]XIU N,ZHANG J.Some recent advances in projection-type methods for variational inequalities[J].J Computational and Applied Mathematics,2003,152(1):559-585.

[5]何诣然.一个关于混合变分不等式问题的投影算法[J].数学物理学报,2007,27(2):215-220.

[6]BAUSCHKE H H,COMBETTES P L.Convex analysis and monotone operator theory in Hilbert space[M].New York:Springer New York,2011.

[7]LI F,HE Y.An algorithm for generalized variational inequality with pseudomonotone mapping[J].Journal of Computational and Applied Mathematics,2009,228(1):212-218.

[8]ALBER Y I,IUSEM A N,SOLODOV M V.On the projected subgradient method for nonsmooth convex optimization in a Hilbert space[J].Mathematical Programming,1998,81(1):23-35.

[9]XIA F Q,HUANG N J,LIU Z B.A projected subgradient method for solving generalized mixed variational inequalities[J].Operations Research Letters,2008,36(5):637-642.

[10]HE Y.A new double projection algorithm for variational inequalities[J].Journal of Computational and Applied Mathematics,2006,185(1):166-173.

[11]邱涛,何诣然.二次投影算法的扰动分析[J].四川师范大学学报(自然科学版),2012,35(1):8-11.

[12]YE M,HE Y.A double projection method for solving variational inequalities without monotonicity[J].Computational Optimization and Applications,2015,60(1):141-150.