基于几何更新方法的轮胎胎面磨耗行为分析

许顺凯，臧孟炎，周　涛

(1.华南理工大学机械与汽车工程学院，广东 广州　510640)(2.万力轮胎股份有限公司，广东 广州　511400)

耐磨性是评价轮胎性能的重要指标，轮胎耐磨性能的好坏不仅影响轮胎的使用寿命，而且与行驶安全息息相关。为此，各大轮胎生产商根据大量的轮胎磨耗统计分析结果制定了相应的标准，在胎面花纹沟处设置胎面磨耗标志。我国国家标准规定，轿车、微型车和轻型载重车胎面的磨耗标志高度不低于1.6mm[1]。胎面磨耗主要原因是胎面和路面之间发生相对滑移，早期的轮胎磨耗性能研究以试验为主[2-3]，由于磨耗试验周期较长，使得轮胎磨耗研究的成本较高。随着计算机技术的发展，CAE技术和分析方法在轮胎磨耗研究方面得到了广泛应用，并取得了较好的效果。ZHENG等[4]运用网格更新和有限元计算结果将胎面磨耗表述成与摩擦能量相关的函数，但是文献中未提及网格更新的具体方法；CHO等[5]根据接地区域的摩擦总能量，利用磨耗模型一次线性外推到指定里程求得磨耗质量以及平均磨耗深度，但是这种一次线性外推法并未考虑磨耗过程中胎面轮廓变化对磨耗的影响；李钊等[6]利用网格更新方法对纵沟槽轮胎和复杂花纹轮胎进行了磨耗分析，获得了较为合理的磨耗结果；ZUO等[7]利用网格更新的方法进行了轮胎多边形磨损的研究，更符合轮胎磨损的实际情况。

本文以205/55/R16型子午线轮胎为研究对象，使用几何更新和有限元方法分析轮胎的磨耗现象，计算轮胎在自由滚动过程中的磨耗量；与汽车道路磨耗试验的测量结果比较，确认仿真分析方法的有效性；对比不进行几何更新和进行几何更新的轮胎磨耗轮廓和数值，说明几何更新方法的准确性。

1　道路试验简介

本次道路试验选用沥青铺设的路面，试验车型为世嘉，试验里程全长20 000km，试验时间23d，单轮承受载荷398kg，轮胎气压为0.23MPa，行驶速度为60km/h。试验过程中，车辆尽可能保持同样的线路和同样的速度行驶，避免出现极限工况。由于本次试验未对行驶工况进行统计，因此本文参考文献[5]和[8]，匀速直线行驶工况占总行驶工况的比例约为84.9%，假设自由滚动工况与其他工况磨耗量近似相等，得到总行驶里程20 000km中自由滚动工况行驶16 980km，磨耗量约为0.993mm。

2　轮胎有限元模型的建立

轮胎建模方法如图1所示。首先建立纵沟槽轮胎的二维有限元网格，然后绕轮胎轴线旋转360°生成三维轮胎模型，并且沿周向非均匀划分48份，使接地端及附近区域的网格较为精细。在有限元模型中，橡胶材料采用不可压缩的超弹性材料模型(YEOH模型)，钢丝帘线使用REBAR单元嵌入橡胶基体单元中。路面使用解析刚体建模，轮胎与路面之间的摩擦模型采用指数衰减模型[9]，即：

μ=μk+(μs-μk)e-dcveq

(1)

式中：μk为动摩擦系数，取0.7；μs为静摩擦系数，取0.9；dc为指数衰减系数，取0.581 6；veq为相对滑动速度。

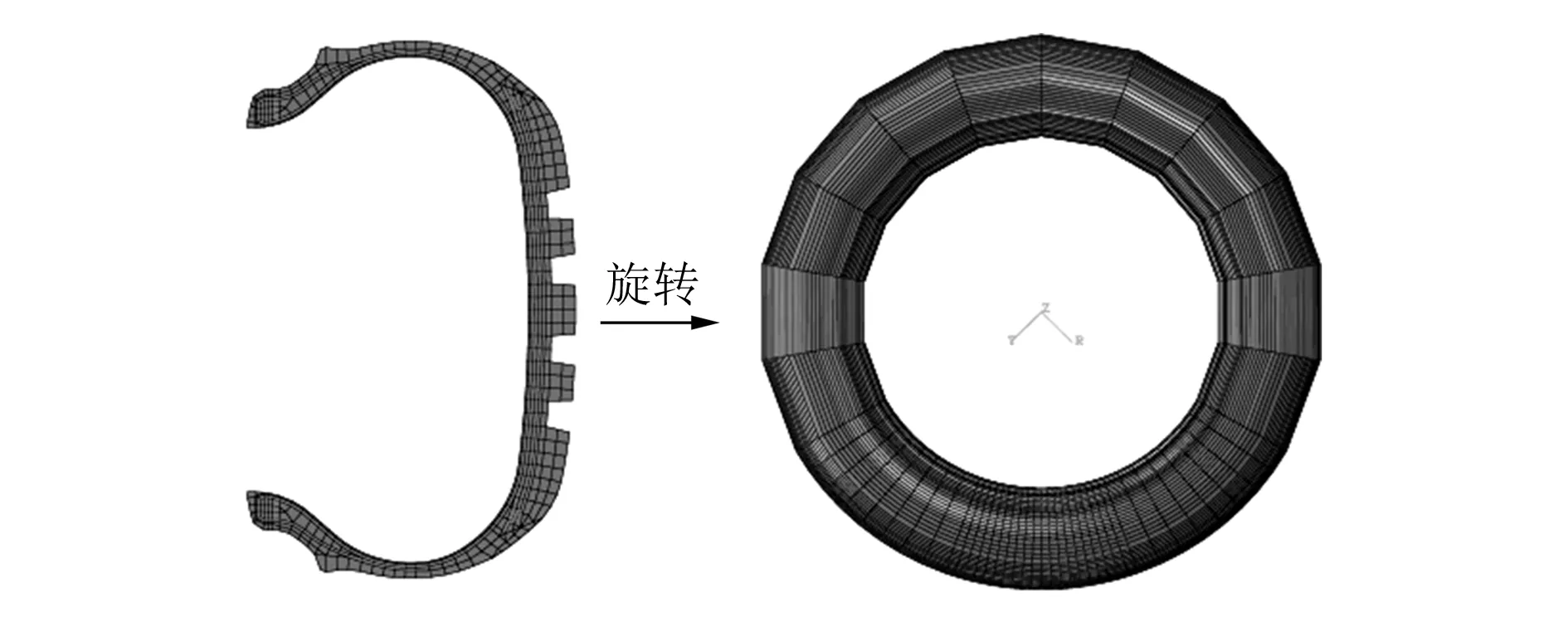
图1　纵沟槽轮胎有限元网格

轮胎充气和加载使用基于拉格朗日描述的隐式算法[10]。轮胎自由滚动使用稳态传输方法，该方法是基于拉格朗日/欧拉混合描述的隐式算法，其核心思想是使用拉格朗日算法描述单元的变形，使用欧拉算法描述刚性转动[6]。

3　磨耗计算过程

基于网格更新方法的轮胎磨耗仿真过程，就是将整个道路磨耗试验过程分为多个阶段，计算每一个阶段内胎面各节点的磨耗深度，根据磨耗深度移动胎面网格节点，模拟胎面橡胶材料的销蚀过程。

3.1　磨耗速率的计算

ARCHARD磨损模型[11]在磨耗预测方面应用广泛，数学表达式为：

(2)

式中：Q为材料的磨耗体积；S为滑移距离；K为无量纲磨损常数；H为接触对中较软材料的布氏硬度；FN为接触面的法向载荷。在轮胎磨耗过程中，磨损常数K=1×103，橡胶的布氏硬度H=2GPa[7]。实际磨耗过程是一个随时间变化的过程，将式(2)对时间取一阶导数得：

(3)

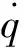
假设纵沟槽花纹轮胎自由滚动状态下磨耗沿周向均匀分布，则单位时间内磨耗体积可表示为[12]：

(4)

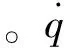
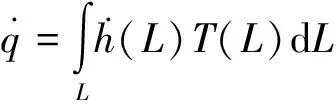
(5)

联立式(4)和(5)计算得：

(6)

将磨耗值离散至胎面周向各节点得：

(7)

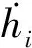
(8)

由于轮胎胎面周向流线带宽度不变，即Ti=T，节点i的接触面积Ai=TΔSi，最终得到磨耗速率关于接触压力与滑移速度的关系表达式为：

(9)

节点n在j时刻的总磨耗深度hj,n由前一个时间增量的累计磨耗深度hj-1,n和当前时间增量内Δt的磨耗深度累加得到，上述过程不断循环即可求解行驶里程内的磨耗值：

(10)

3.2　磨耗方向的确定

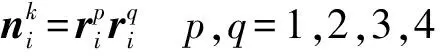
(11)

(12)

(13)

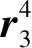
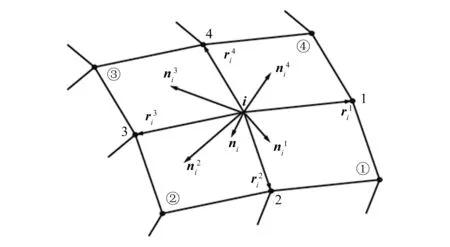
图2　非边缘节点平均内法向

图3　边缘节点移动方向

3.3　网格畸变的处理

轮胎磨耗仿真过程通过移动胎面节点更新胎面几何形状，但是移动胎面节点可能会严重影响轮胎内部网格质量。图4(a)为网格的原始形状，移动网格节点造成网格扭曲变形严重如图4(b)所示，因此要对轮胎内部网格重新划分，减小网格扭曲与变形，如图4(c)所示。

本文采用ABAQUS自适应网格划分技术(ALE)来保持网格单元的质量。该方法在大变形或材料损失的情况下允许网格独立于材料进行移动，并且不改变网格的拓扑结构。在具体应用ALE的过程中，每当增量步收敛时,ABAQUS软件就会自动调用用户子程序UMESHMOTION移动胎面网格节点，同时进行内部网格平滑处理，提高网格质量。

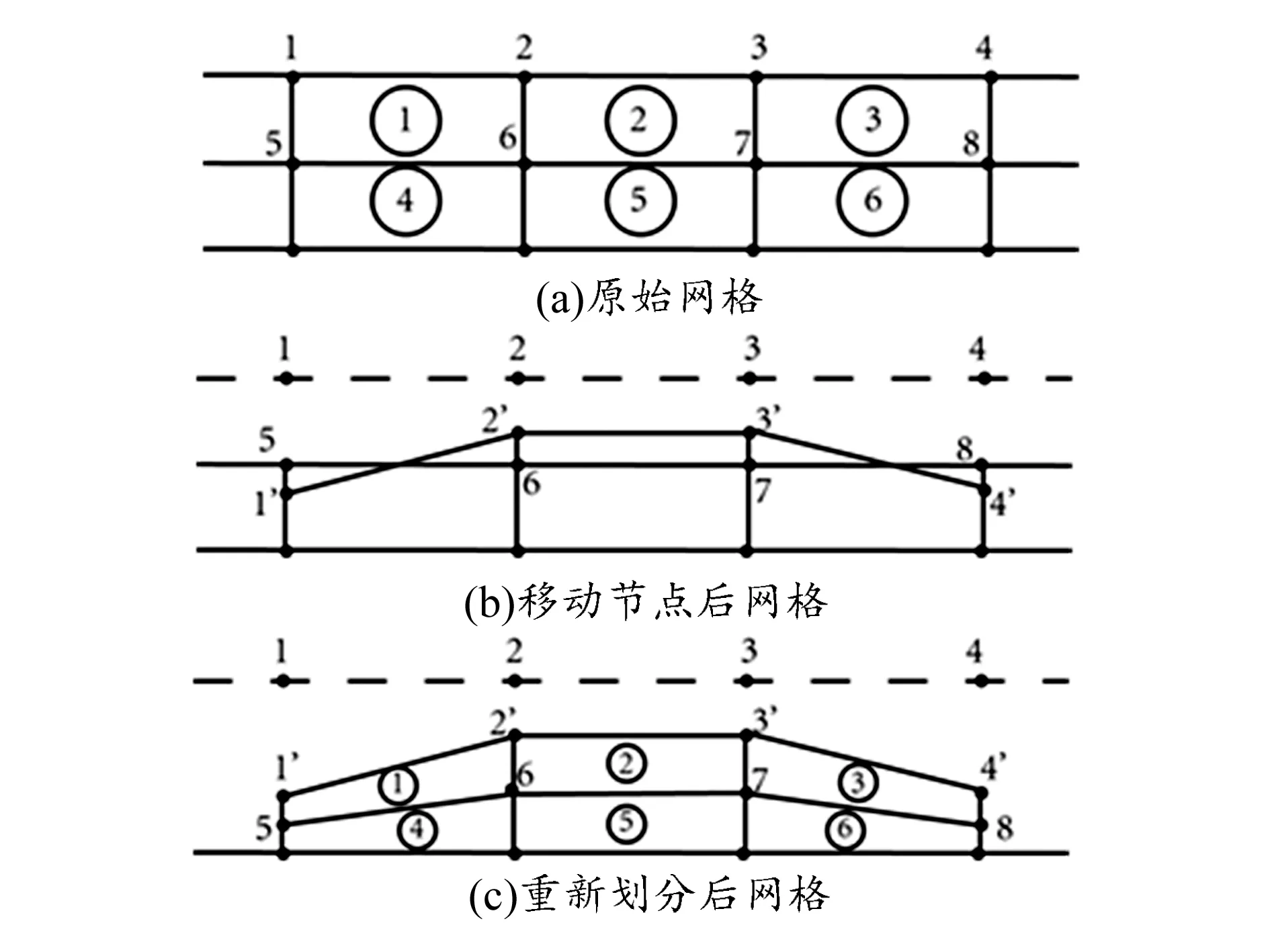
图4　边界节点移动及网格重划分过程

4　轮胎胎面磨耗计算

4.1　自由滚动胎面磨耗计算

利用上述纵沟槽轮胎有限元模型以及磨耗求解策略，分析轮胎自由滚动16 980km的磨耗过程。整个磨耗分析过程分为8个阶段，大致每2 000km的行驶里程确定为一个分析阶段。利用稳态传输的方法模拟轮胎自由滚动1s，计算1s内轮胎磨耗量。将该磨耗量乘以匀速行驶2 000km所用的时间作为一个阶段结束时的总磨耗量，并以此作为输入条件更新单元节点位置。这种常值外推放大技术[14]可以降低磨耗问题的计算成本，一个有限元分析过程就代表了一个阶段内的磨耗过程。

图5为自由滚动过程中沿胎宽方向磨耗深度随行驶里程变化分布。从图中可以看出，沿胎宽方向的磨耗量几乎左右对称，但左侧磨耗值略大于右侧，且靠近胎肩处花纹磨耗值较大而胎冠中部花纹磨耗较小。轮胎自由滚动过程中，由于轮胎内部结构不对称，产生胎体锥度和帘线层转向效应[15]，对轮胎力学性能的影响相当于小外倾角和小侧偏角的作用，从而使胎面左右两侧花纹磨耗深度存在差异；轮胎接地时在胎侧刚度的影响下，胎肩部位接触压力增大，胎冠部位向中间挤压，接地区域中部压力较小而两侧压力较大，造成靠近胎肩处花纹磨耗严重，而胎冠中部花纹磨耗较小，这与实际道路行驶中车轮的磨耗趋势较为一致。仿真分析得到轮胎自由滚动行驶16 980km里程的最大磨耗量为0.905mm，与整车道路磨耗试验中的轮胎最大磨耗值0.993mm在同一数量级范围内，证明了仿真分析方法的有效性。

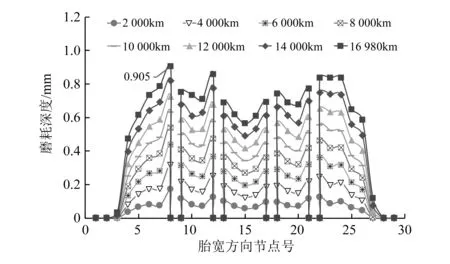
图5　沿胎宽方向磨耗数值分布

图6为轮胎胎面磨耗情况分布图，图中沟槽和胎侧为无磨耗区域，花纹带外表面为发生磨损的区域，且越靠近胎肩磨耗越严重，磨耗最大数值为0.905mm，与图5中磨耗深度分布曲线相对应。图7(a)为轮胎横截面磨耗分布图，图7(b)为局部放大图。图中节点1到节点9表示轮胎原始网格节点位置，节点1′到节点9′表示磨耗后轮胎最终节点位置，箭头表示节点移动方向。在计算完成一个阶段内胎面各节点的磨耗深度后更新胎面的几何轮廓，再进行下一个阶段的磨耗分析。

图6　胎面磨耗分布图

图7　轮胎横截面的网格节点移动

图8为行驶过程中轮胎沿胎宽方向的磨耗速度分布。从图中可以看出，胎面磨耗速度随着行驶里程的增加而发生变化：轮胎滚动初始阶段花纹边缘处磨耗速度较快；胎面非边界处，磨耗数值大小变化比较平稳，并且随着行驶里程的不断增加，胎面各处磨耗速度趋于平稳状态，这与实际行驶过程中轮胎正常磨耗的现象相吻合。

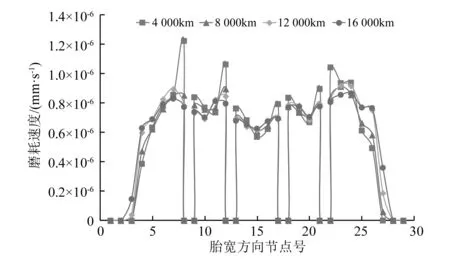
图8　沿胎宽方向磨耗速率分布

4.2　两种计算方法的磨耗分布对比

使用同一轮胎模型，分析不进行几何更新情况的轮胎磨耗。不进行几何更新，即利用轮胎滚动1s的磨耗量一次线性外推到指定里程求得磨耗深度。图9中方法一为采用不进行几何更新方法计算沿胎宽方向的磨耗分布，方法二为采用几何更新方法计算沿胎宽方向的磨耗分布。由图可知，方法一得出的磨耗分布导致各条花纹带边缘处磨耗值突变严重。因为不进行几何更新，忽略了轮胎滚动过程中胎面接地压力的变化。实际磨耗过程中胎面几何形状会随着磨耗过程的进行不断发生变化，造成胎面接地压力的分布改变，影响了胎面的磨耗行为，因此磨耗计算过程中适当的几何更新有利于提高轮胎磨耗仿真分析精度。由表1可得，方法一和方法二的磨耗平均值相差4.9%，说明两种方法在计算平均磨耗深度方面差别不大；但是磨耗深度分布有较大差异，且方法一磨耗最大值与实验值的误差达到37.76%，方法二磨耗最大值与实验值误差为8.86%，充分说明了基于几何更新的方法在计算磨耗分布问题上的有效性。

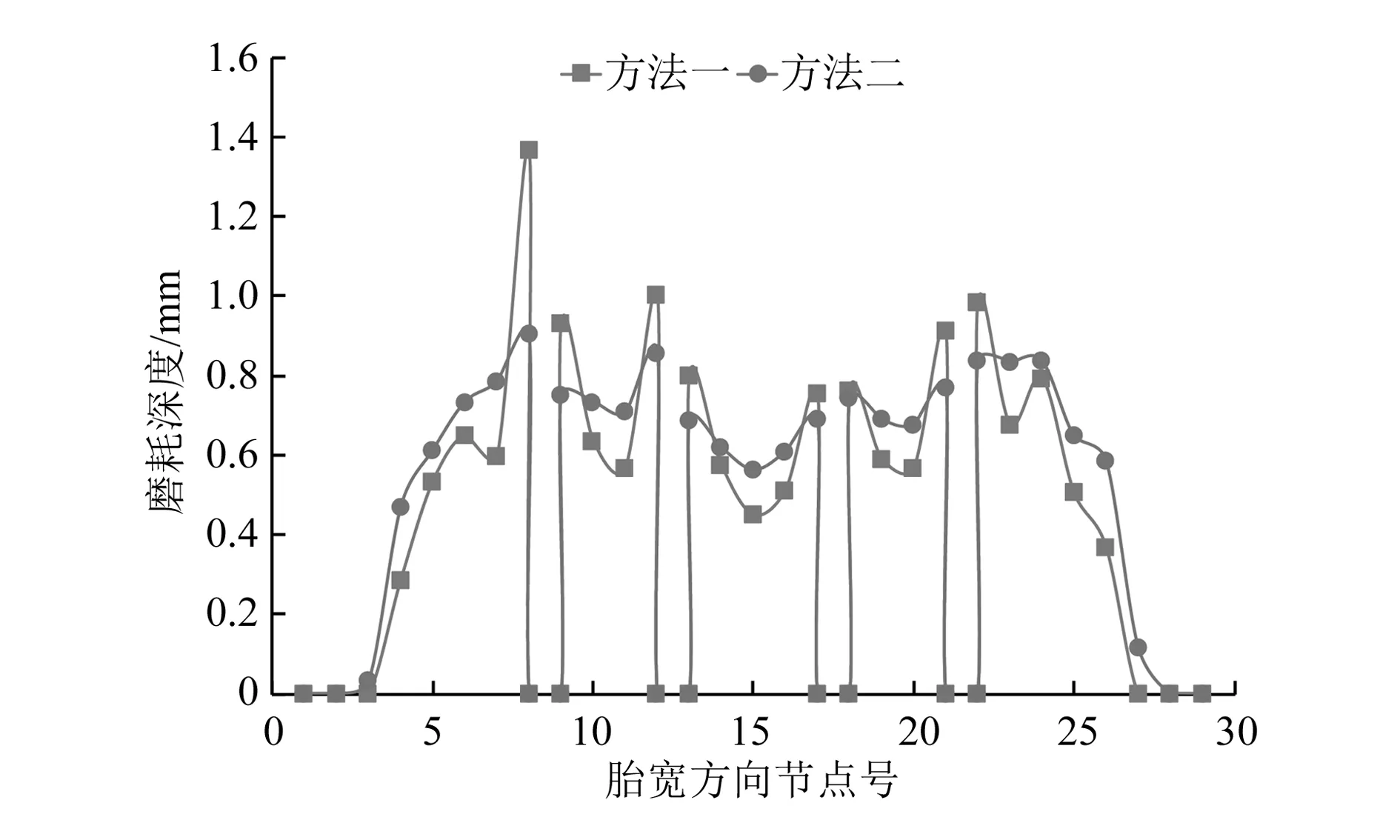
图9　两种磨耗方法的磨耗数值分布对比

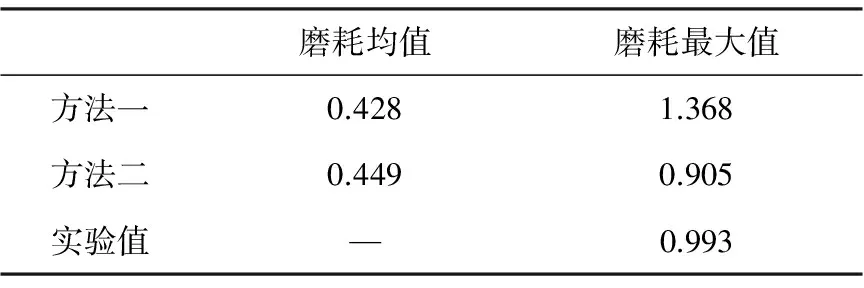
表1　两种磨耗方法的磨耗数值对比 mm

4.3　外倾角对磨耗的影响

车轮外倾角是车轮定位的重要参数。定位准确的外倾角可以提高制动时的方向稳定性和转向轻便性。同时，外倾角定位准确与否对车轮的磨耗行为也具有导向性，主要决定磨耗的分布趋势[16]，外倾角为正值，轮胎外侧磨损较为严重，反之内侧磨损严重。

正确定位车轮外倾角，满载后车轮会与拱形路面几乎垂直，从而减少轮胎偏磨损现象。为研究外倾角定位对胎面偏磨损的影响，仿真分析满载时左前轮0.0°外倾角、0.5°外倾角、1.0°外倾角3种情况下胎面磨耗分布情况。由图10可以看出，0.0°外倾角时左侧胎面花纹磨损略大于右侧花纹，并且随着外倾角逐渐增加，轮胎外侧花纹带磨损逐渐加剧，而内侧花纹带磨损逐渐减轻，轮胎发生偏磨损现象，这种偏磨损现象也成为判断车轮外倾角定位不准确的重要标志。

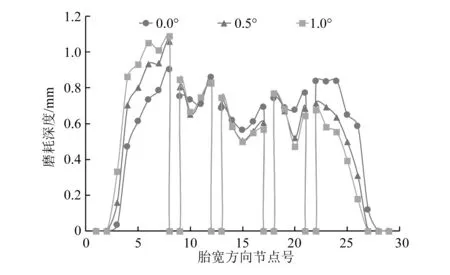
图10　不同外倾角时磨耗分布情况

5　结束语

本文利用几何更新法仿真分析纵沟槽轮胎自由滚动过程中的磨耗行为。将整个磨耗分析过程离散化，对每一阶段内的磨耗问题单独进行求解，结合常值外推放大技术对磨耗后轮胎的几何边界进行更新。与不进行几何更新的胎面磨耗仿真结果相比，几何更新方法得到了更加接近实验结果的最大胎面磨耗量。另外，考虑车轮定位角的作用，分析了外倾角对胎面磨耗分布的具体影响，即外倾角越大，轮胎发生偏磨损的现象越严重。

参考文献：

[1]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.轿车轮胎:GB9743—2007[S].北京：中国标准出版社,2007.

[2]SOUTHERN E. Rapid tire wear measurements using a two‐wheeled trailer[J]. Tire Science & Technology, 1973, 1(1):3-16.

[3]BRENNER F C. Effect of tire wear on wear rate[J]. Tire Science & Technology, 1975, 3(4):235-251.

[4]ZHENG D. Prediction of tire tread wear with FEM steady state rolling contact simulation[J]. Tire Science & Technology, 2003, 31(3):189-202.

[5]CHO J R, CHOI J H, KIM Y S. Abrasive wear amount estimate for 3D patterned tire utilizing frictional dynamic rolling analysis[J]. Tribology International, 2011, 44(7/8):850-858.

[6]李钊. 轮胎胎面磨耗行为的实验研究与数值分析[D]. 合肥：中国科学技术大学, 2013.

[7]ZUO S G, NI T X, WU X D, et al. Prediction procedure for wear distribution of transient rolling tire[J]. International Journal of Automotive Technology, 2014, 15(3):505-515.

[8]SMITH K R, KENNEDY R H, KNISLEY S B. Prediction of tire profile wear by steady-state FEM[J]. Tire Science & Technology, 2008, 36(4):290-303.

[9]吴侃. ABAQUS环境下的瞬态滚动轮胎磨损量分布的计算方法研究[D].上海：同济大学, 2011.

[10] 姜明磊. 全钢子午线轮胎疲劳寿命仿真研究[D]. 广州：华南理工大学, 2016.

[11] ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of Applied Physics, 1953, 24(8):981-988.

[12] 赵亚元.子午线轮胎胎面磨耗性能的有限元分析[D].青岛：青岛科技大学，2015.

[13] 宿月文, 陈渭, 朱爱斌,等. 滑动磨损过程有限元分析及销磨损预测[J].中国机械工程, 2009, 20(13): 1573-1576.

[14] KIM N H, WON D, BURRIS D, et al. Finite element analysis and experiments of metal/metal wear in oscillatory contacts[J]. Wear, 2005, 258(11/12): 1787-1793.

[15] 卢荡, 郭孔辉. 轮胎结构不对称性对其力学特性建模的影响[J]. 吉林大学学报(工学版), 2004, 34(2):185-188.

[16] 黄海波. 轿车轮胎非正常磨损机理及使用寿命预测研究[D].上海：同济大学, 2006.