轮毂轴承轴铆合过程CAE分析及验证

曲　杰，胡焱松, 徐　梁

(华南理工大学机械与汽车工程学院，广东 广州　510640)

轮毂轴承是为轮毂的转动提供精准导向的汽车零部件，在承受轴向载荷的同时还承受径向载荷，直接影响汽车的经济性、安全性和舒适性[1]。随着现代制造技术的不断发展和提高，轴铆合装配的轮毂轴承单元以其高可靠性、集成化和轻量化等特点，在汽车工业中获得了广泛的应用[2]。

轴铆合过程较为复杂，不少国内外学者应用CAE分析方法对轮毂轴承轴铆合的成型工艺过程进行了探究分析[3-4]，通过有效的有限元模型分析各项工艺参数对轮毂轴承的性能及寿命的影响，可缩短轮毂轴承的开发周期并提高产品质量。如何获得轴铆合过程中真实有效的参数，包括材料参数、摩擦系数、运动轨迹等，对获得准确有效的有限元模型至关重要，在此基础上，如何进一步降低轴铆合过程仿真分析计算机资源的消耗也是现代绿色设计的重要环节。

1　轮毂轴承轴铆合原理及性能参数分析

1.1　轴铆合原理

轴铆合原理如图1所示，铆头沿一定轨迹进行空间运动，铆头成型曲面通过与轮毂轴端接触使之发生合理的塑性变形从而产生需要的轴向预紧力。

1.2　轮毂轴承性能参数

国内外大量研究表明，轮毂轴承的轴向游隙、轴向预紧力等直接影响其寿命[5-6]，通过轴铆合原理可知轮毂轴承的各项性能参数需要在成型过程中得到保障。

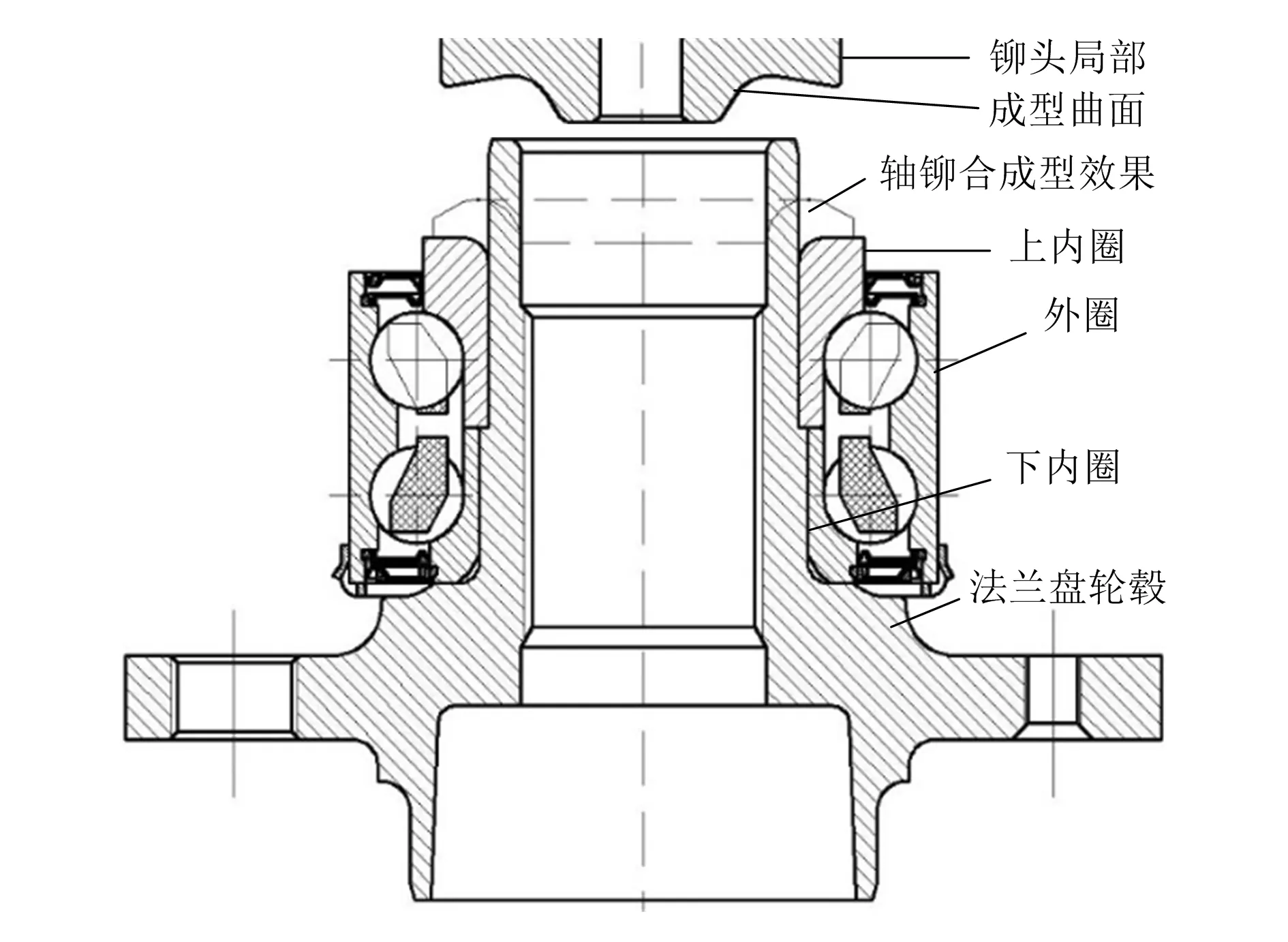
图1　轮毂轴承轴铆合原理示意图

轮毂轴承的轴向游隙S由轮毂轴端的塑性变形对轴承内圈形成一定的轴向预紧力Fc而产生，如果预紧力过大，轴承内部的摩擦力矩也会增大，会导致输出力矩损耗增大，从而增加了整车的油耗，故要求预紧力越小越好。从轴向游隙与汽车轮毂轴承的性能曲线(图2 )[5]可知，预紧力过小无法保证较为合理的轴向游隙，会使轮毂轴承的系统寿命降低。

为了平衡轮毂轴承的系统寿命以及其对整车性能的影响，需要将轮毂轴承轴向游隙和轴向预紧力控制在一个较为合理的范围内。刘佳[7]通过大量配合试验得到预紧力、轴向游隙、轴承寿命的关系，如图3所示。

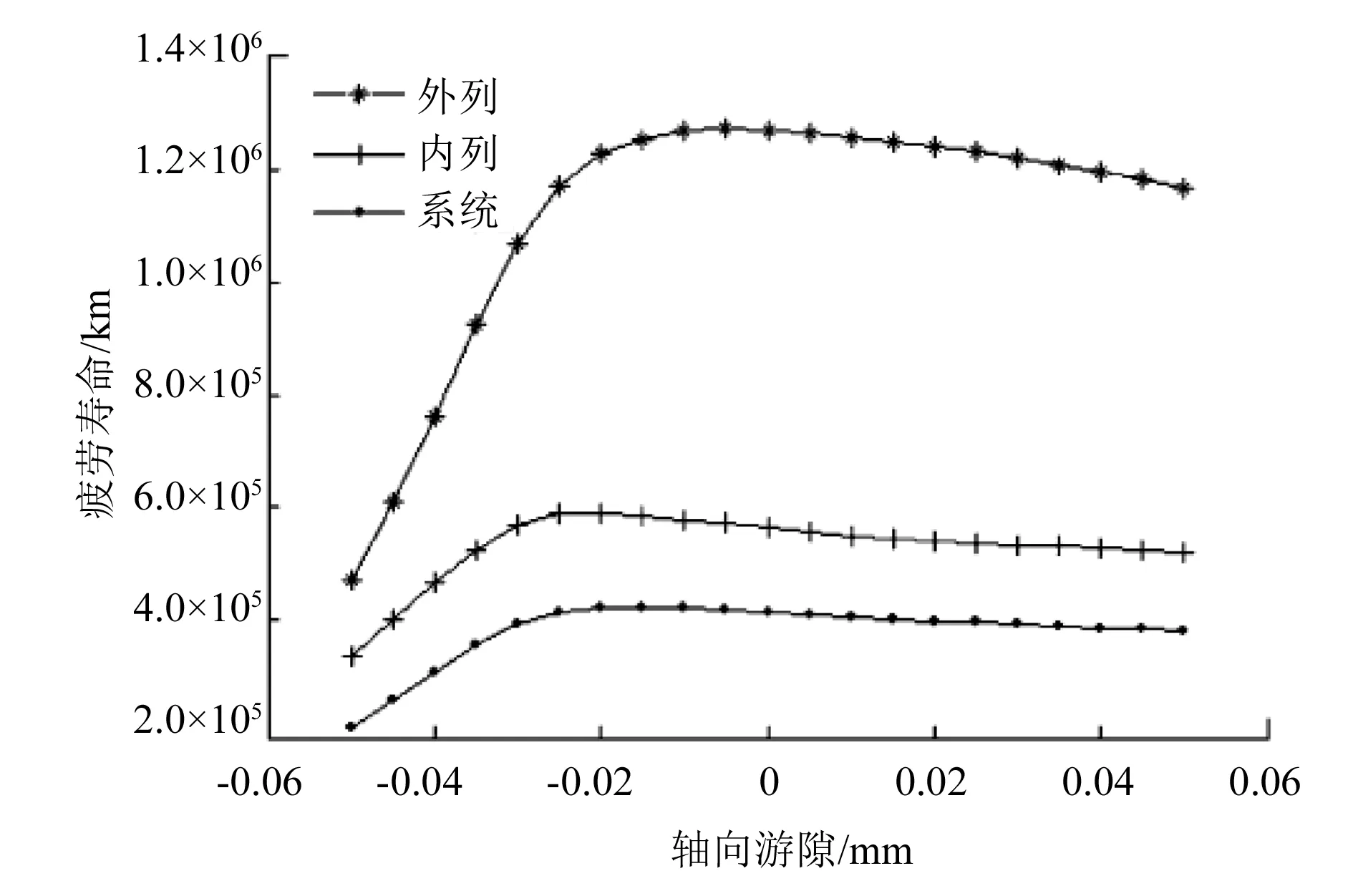
图2　轴向游隙对轮毂轴承单元疲劳寿命的影响

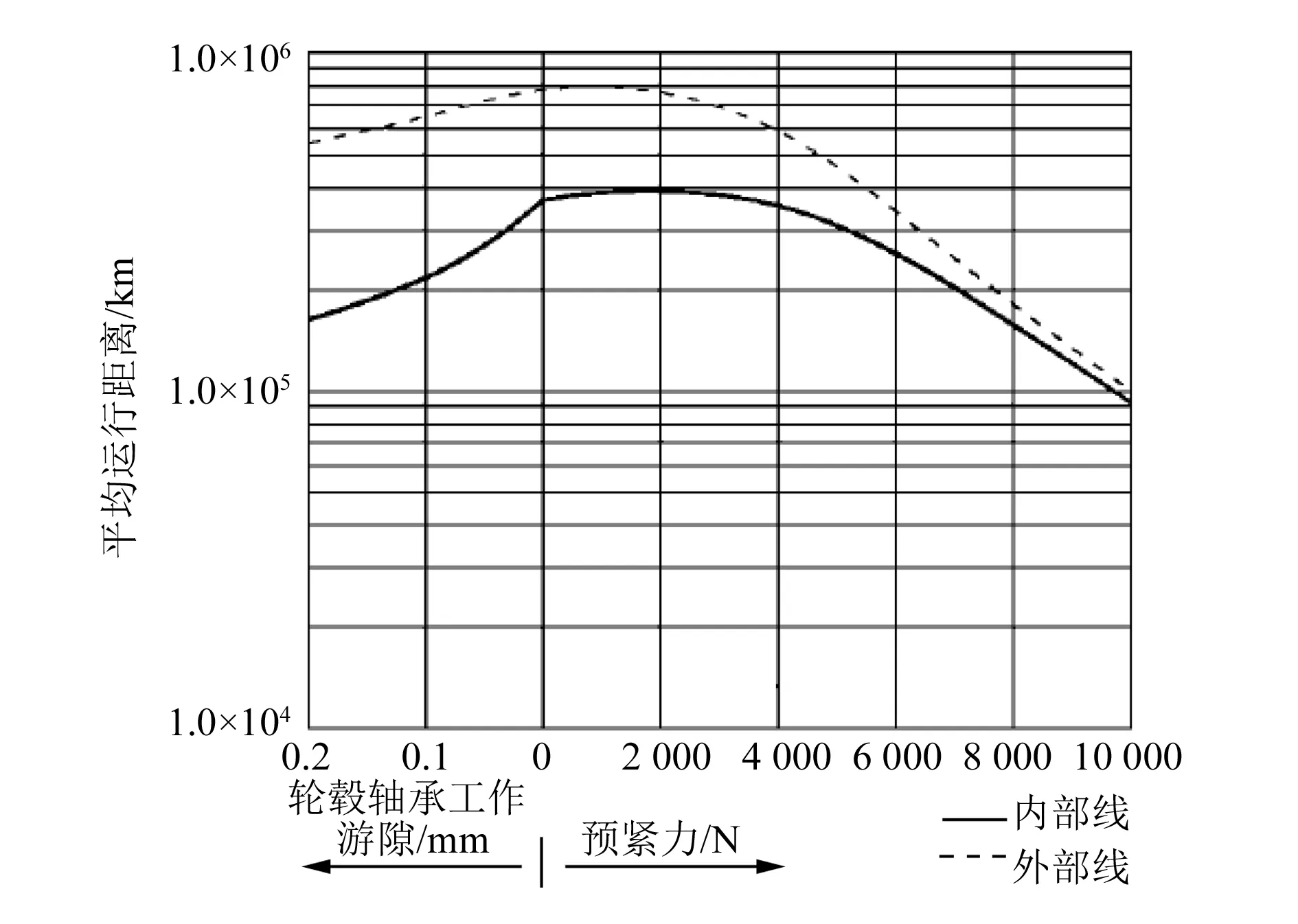
图3　轮毂轴承轴向游隙、预紧力、轴承寿命关系图

图3以对应的预紧力表征负游隙，与图2的表征效果相符。

基于以上分析以及浙江万向集团的黄德杰等[8]对相同系列的第三代轮毂轴承单元的测量计算研究，可以得到当轴铆合过程中产生负轴向游隙 在10μm～40μm之间，轴向预紧力 在3kN～7kN之间时，能使轮毂轴承有较高的系统寿命，同时令整车获得较好的燃油经济性。

2　轴铆合过程关键参数确定

基于一定的数据和测量，应用CATIA和HyperMesh进行前处理，得到应用于分析计算的有限元模型。根据试验和理论推导获得轮毂轴承轴铆合工艺过程的材料参数、摩擦系数、铆头空间运动轨迹。通过合理的参数设置，得到计算效率更高的轴铆合有限元模型。

2.1　材料参数确定

轮毂轴承单元的轮毂，上下内圈均采用大量应用于汽车零部件的40Cr，铆头采用GCr15，构造轴铆合有限元模型时需要得到相关材料参数，包括弹性模量、密度、泊松比以及真实应力-应变曲线。通过查询机械材料手册[9]，得到40Cr和GCr15的基本材料特性见表1。

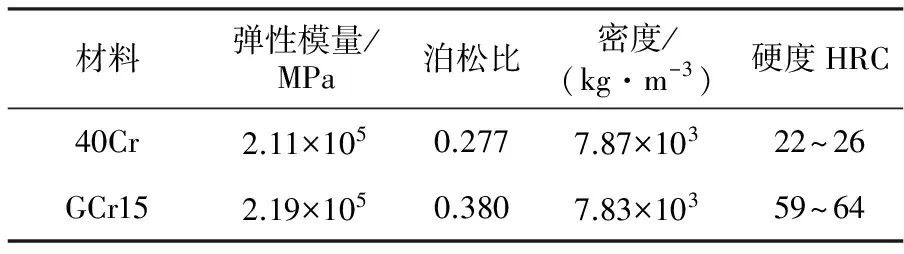
表1　40Cr以及GCr15的基本材料特性

在整个轴铆合的工艺过程中，主要探究轮毂轴端的塑性变形特点，且应用GCr15材料的铆头硬度远大于轮毂轴端的硬度，故将铆头作为刚体处理。

为了保证仿真分析与实际成型工艺的一致性，结合实际材料状态，对40Cr进行调制处理，并按照《金属材料室温拉伸试验方法》(GB/T228—2010)对40Cr的试样进行3种不同应变速率(0.001s-1，0.01s-1，0.1s-1)下的标准单向拉伸试验，通过名义应力应变与真实应力应变的转换公式(1)和(2)，获得40Cr的真实应力-应变曲线，如图4所示。

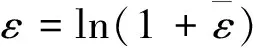
(1)

(2)

图4　40Cr在不同应变速率下的真实应力-应变曲线

从图4可以看出，40Cr有较为明显的弹性阶段、屈服阶段、强化阶段和颈缩阶段，且应变速率对40Cr的真实应力应变曲线的影响并不大。

2.2　摩擦系数确定

轴铆合过程中，铆头绕着中心做不间断的摆动，与轮毂轴端的接触不断地发生改变，同时铆头与轮毂轴端也发生相对滑移，故在ABAQUS/Explicit中选用库仑摩擦模型来确定接触关系[10]。依据库仑定律，接触表面的摩擦力(剪应力)与摩擦系数之间的关系式为：

(3)

式中：τ为摩擦剪应力；μ为摩擦系数；σv为有效流动应力。可知摩擦系数对轴铆合结果影响较大，采用圆环墩粗试验方法确定铆头与轮毂轴端接触的摩擦系数。

根据JB/T 7708—1995的相关要求，选定圆环材料为40Cr，采用拉伸试验相同的热处理工艺，按照圆环尺寸要求，即外径∶内径∶高=6∶3∶2，得到符合要求的试样，如图5所示。

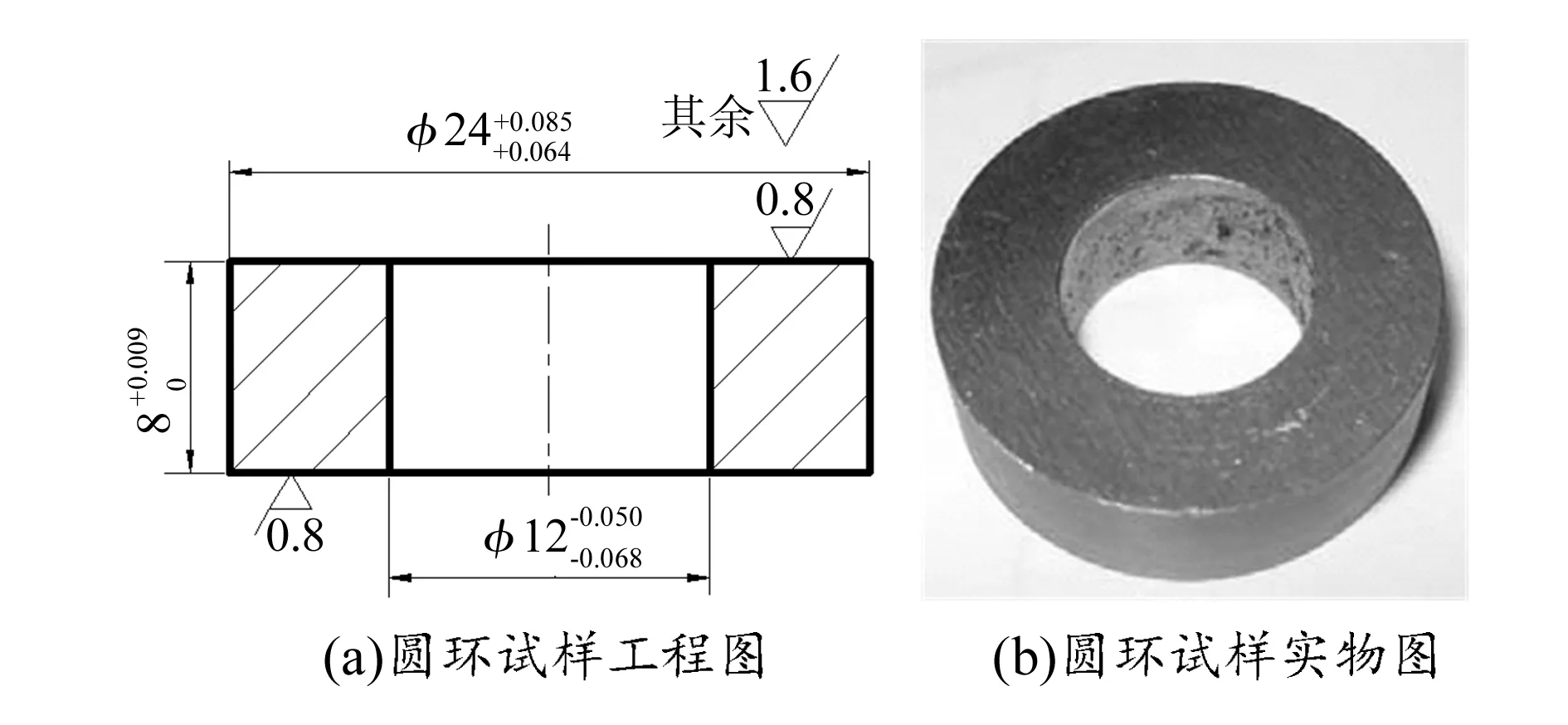
图5　圆环墩粗试样

结合相关标准要求，保证圆环试件的压缩率为45%～55%，分别在不同的应变速率(10s-1,1s-1,0.1s-1,0.01s-1)下进行试验，并根据式(4)得到不同速率下圆环试件的压缩率H和内径变化率D：

(4)

式中：h0为初始高度；h1为墩粗后高度；d0为初始内径；d1为墩粗后内径。通过测量和计算得到圆环墩粗试验的结果见表2。

由表2可知，在相同下压量下，应变速率对圆环压缩率的影响并不大，内径的变化率却随着应变速率的增大而减小，可知应变速率对试样内侧金属的流动有一定影响。

基于2.1节得到的40Cr的材料参数，按照实际试验的要求，在ABAQUS中设置一系列摩擦系数(0.01, 0.06, 0.08, 0.10, 0.12, 0.15, 0.18, 0.20, 0.23, 0.25, 0.30, 0.40)的情况下进行墩粗试验仿真，下压量为6mm，应变速率为1s-1，得到的圆环墩粗仿真结果如图6所示。

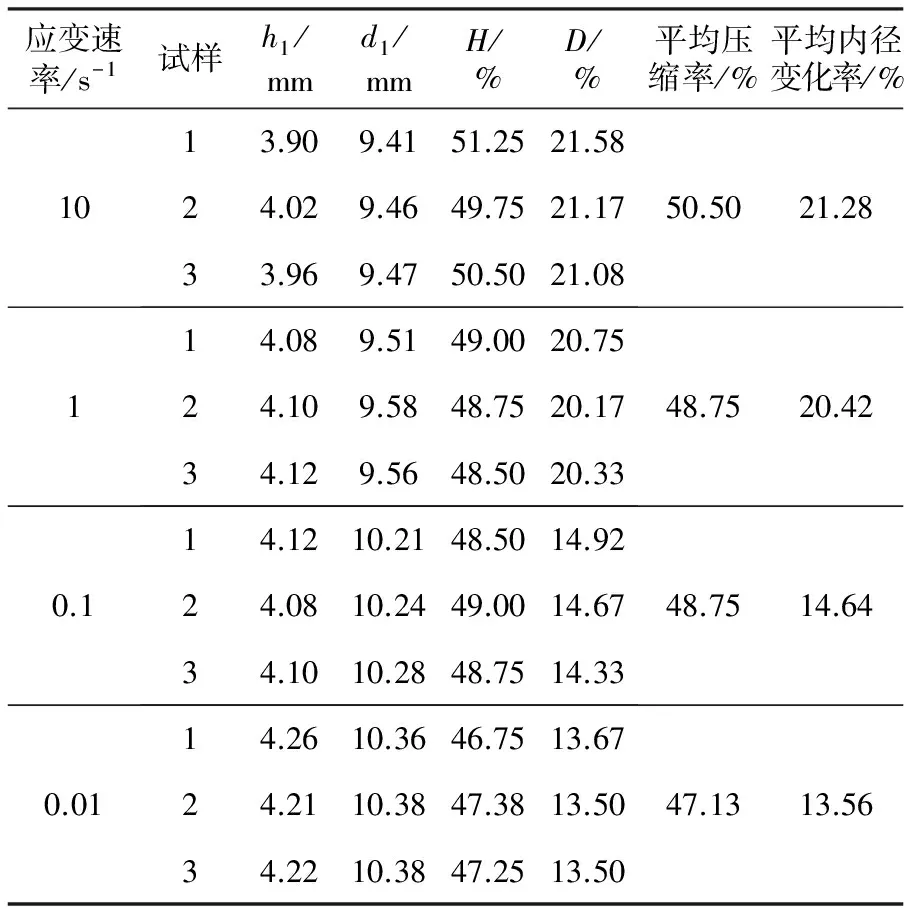
表2　圆环墩粗试验结果

从图6可知，圆环墩粗时，40Cr的径向流动状态与摩擦系数有关。当摩擦系数比较小时，圆环试样的内径和外径均增大，金属径向流动方向均向外；当摩擦系数大于某一临界值时，圆环试样外径增大，内径减小，外层金属向外流动，内层金属向内流动，仿真结果与理论结果保持一致。

基于仿真结果，得到在ABAQUS计算中40Cr的摩擦系数曲线如图7所示。

从图7可知，40Cr材料的摩擦系数在0.20～0.25之间，整个工艺过程中的载荷是一直变化的，故取不同应变速率下的摩擦系数的均值能更好地反映真实的轴铆合工艺过程中的摩擦系数，根据试验和仿真结果确定铆头与轮毂轴端接触的摩擦系数为0.22。

2.3　空间运动轨迹确定

铆头通过做轴向进给运动和绕着空间中某一点做11 瓣梅花轨迹运动来实现轮毂轴承的铆合过程。

通过分析可知，其梅花运动轨迹是由外啮合齿轮Z1的公转以及与内啮合齿轮Z2的内啮合转动而形成的平面摆线运动[11]，为了得到铆头控制点M的11瓣梅花运动轨迹，令运动轨迹通过圆心O2，且偏心距e=R-r，得到简化后的内外啮合运动简图如图8所示。

图6　圆环在不同摩擦系数时的墩粗仿真结果

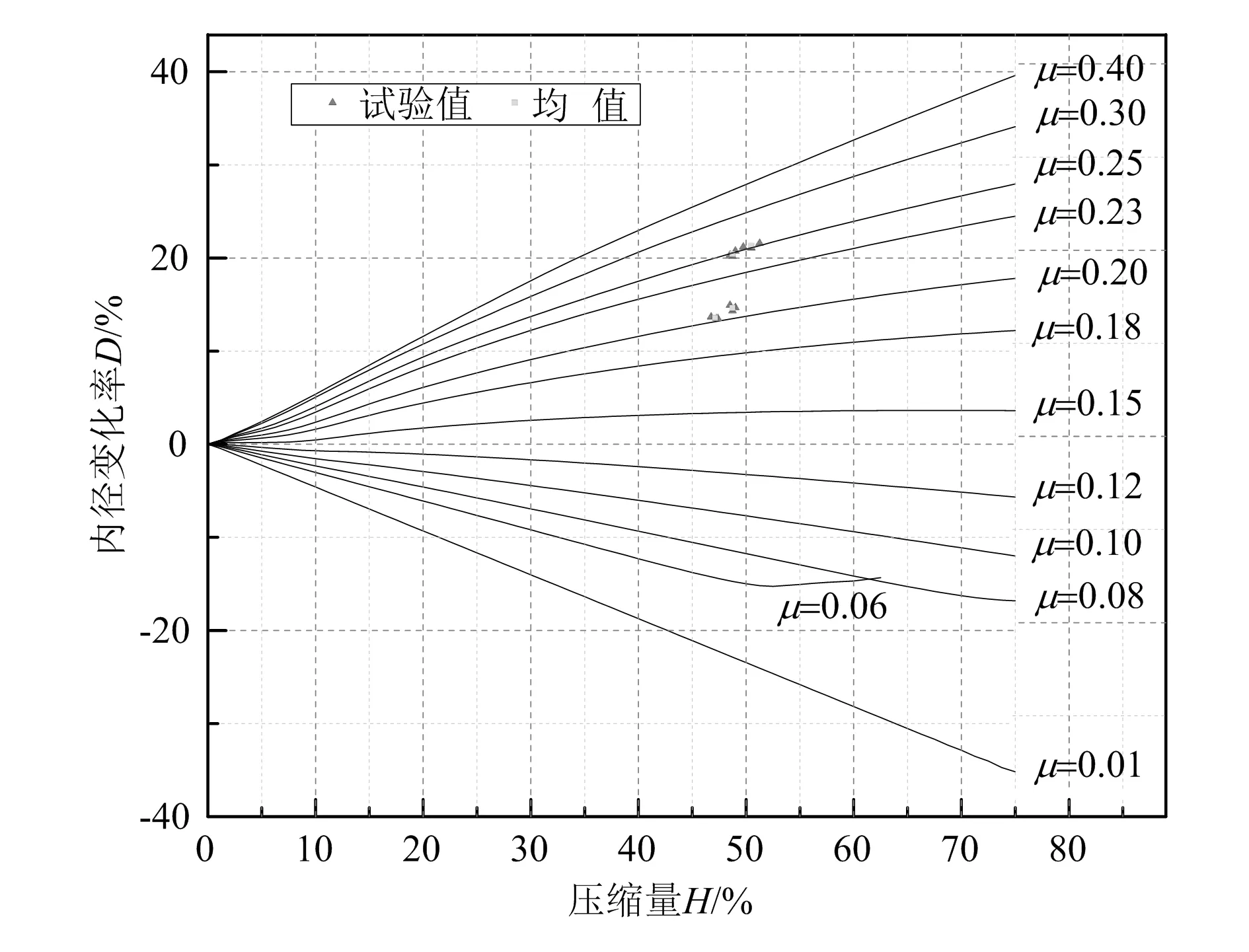
图7　40Cr圆环墩粗法得到摩擦系数曲线图

图8　外齿轮与内齿轮啮合运动简图

通过欧拉角法和一系列的变换，得到铆头三轴的角速度方程为[12]：

(5)

式中：ωx为绕x轴的角速度;ωy为绕y轴的角速度；ωz为绕z轴的角速度；ω为外啮合齿轮的角速度；R为内啮合齿轮节圆半径；r为外啮合齿轮节圆半径；βmax为铆头的最大偏转角(章动角)。

通过查询JM40-PLC径向铆装机的相关参数配置获得主轴转速N主轴=1 018r/min、外齿轮转速N自转=1 125r/min等相关参数，并基于式(6)和(7)的计算，得到铆头控制点M做11瓣梅花空间运动曲线的相关参数,见表3。

(6)

(7)

式中：OM为点M与铆头底端中心点O的距离。

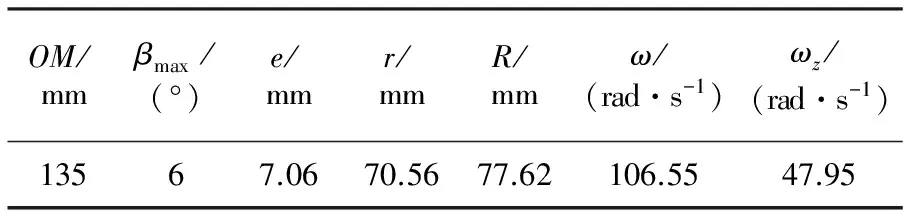
表3　铆头控制点M做11瓣梅花空间运动曲线的相关参数表

将表3中参数代入式(5)即可得到铆头控制点M的空间三轴的角速度运动方程为：

(8)

对三轴的角度进行积分运算可得到控制点M的空间运动轨迹，如图9所示。

图9　控制点M的空间运动轨迹

利用WY-50光栅传感器来获得铆头的轴向进给运动情况，将得到的数据利用origin进行光滑处理，得到铆头控制点的轴向运动轨迹，并对其进行求导得到铆头控制点的轴向速度曲线,如图10所示。

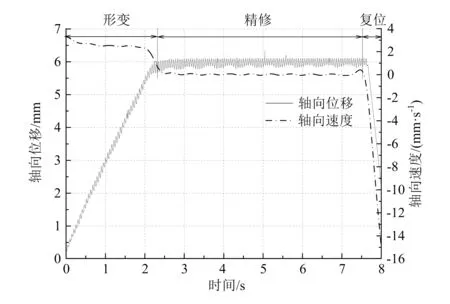
图10　铆头控制点轴向运动轨迹与轴向速度曲线图

2.4　自适应网格策略确定

轴铆合过程中，会产生极大的塑性变形导致网格发生较大的畸变，不仅会产生误差，降低计算效率，甚至会导致计算不收敛而终止。ALE自适应网格方法能够有效解决金属塑性变形而导致的网格畸变问题，提高计算的有效性。对比进行ALE自适应网格设置前后网格情况如图11所示。

图11　有无ALE设置的最终网格质量效果图

从图11可知，无ALE设置分析完成后网格的形状不规整，发生较大的扭曲，由此可知ALE设置能够在发生较大塑性变形过程中获得较好的网格质量。

只有形变阶段发生较大的塑性变形，故可将轴铆合过程分为两个载荷步进行分析：step1为0～2.5s时的形变阶段；step2为2.5～8.0s时的精修和复位阶段。由于ALE自适应网格方法会增加计算时长，为了提高计算效率，仅对step1中有较大塑性变形轮毂轴端部分进行ALE自适应网格设置。

3　轮毂轴承轴铆合过程分析及验证

3.1　成型效果对比分析

通过以上的分析和设置，应用ABAQUS/Explicit对轮毂轴承轴铆合有限元模型进行求解计算，得到有限元结果，其中轮毂轴端轴向载荷曲线如图12所示。

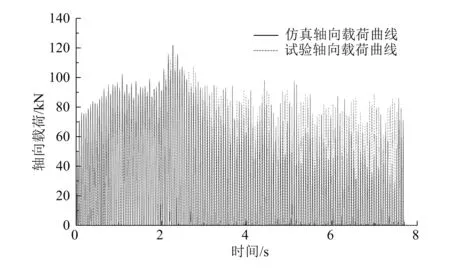
图12　轮毂轴端轴向载荷曲线

由图12可知，在轴铆合过程中，轴向载荷的仿真结果与试验结果基本保持一致，得到最大的轴向载荷为121.798 9kN，试验测得的最大轴向载荷为117.252kN，两者相对误差仅为3.88%。

基于有限元模型计算得到轮毂轴承单元仿真成型效果及应力云图如图13所示，而实际的成型效果如图14所示。

图13　轮毂轴承单元仿真成型效果及应力云图

图14　轮毂轴承单元实际成型效果图

从图13，14可知，仿真成型效果与实际加工的成型效果基本上保持一致。由图13可知，最大应力值为800.9MPa，且应力分布较为均匀，符合实际生产要求。

3.2　性能参数有效性分析

根据轮毂轴承单元的性能参数分析可知，轮毂轴承的轴向预紧力和轴向游隙应在合理的经验值范围内。

轴铆合仿真分析得到的轴向预紧力随时间变化的曲线如图15所示。

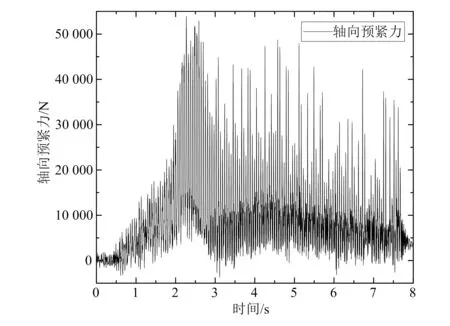
图15　轴向预紧力随时间的变化曲线

从图15可以得到最终的轴向预紧力为4.732kN，通过对仿真结果的测量，可得到轮毂轴承单元的负轴向游隙为25.933μm，轴向预紧力和负轴向游隙均在合理范围内，进一步验证了轴铆合有限元模型的有效性。

综合以上成型效果的对比分析和轮毂轴承性能参数的有效性分析，可以确定整个轮毂轴承轴铆合过程的有限元模型是有效的，能够准确地模拟实际轴铆合加工情况。

4　结束语

本文介绍了轮毂轴承轴铆合成型原理，并分析了轮毂轴承的重要性能参数及其合理的经验取值范围，为轮毂轴承的性能参数确定提供一定的基础。根据试验以及理论推导详细介绍了轴铆合过程中重要参数的确定，包括材料应力应变曲线、摩擦系数、铆头空间运动曲线以及ALE自适应网格策略。最后得到轮毂轴承单元仿真成型效果与实际成型效果基本保持一致，且仿真得到的最大轴向载荷与实际测量值之间的相对误差仅为3.88%，轴向预紧力和轴向游隙也均在合理的取值范围内，验证了轮毂轴承轴铆合过程有限元模型的有效性，能够较为真实地模拟出实际加工过程，为轴铆合过程的数值化分析及设计提供了一定的基础。

参考文献：

[1]陈雪峰, 卫瑞元. 汽车轮毂轴承疲劳失效分析[J]. 轴承, 2009 (3): 30-32.

[2]刘汝卫, 张钢, 殷庆振, 等. 汽车轮毂轴承的发展现状及趋势[J]. 现代机械, 2009(6):78-80.

[3]MOONH K, LEE M C, JOUN M S. An approximate efficient finite element approach to simulating a rotary forming process and its application to a wheel-bearing assembly[J]. Finite Elements in Analysis and Design, 2007, 44(1): 17-23.

[4]NAM C H, LEE M C, EOM J G, et al. Finite element analysis model of rotary forging for assembling wheel hub bearing assembly[J]. Procedia Engineering, 2014, 81: 2475-2480.

[5]黎桂华. 轴向游隙对轿车轮毂轴承性能影响[J].轴承，2011(1) :1-3.

[6]TODA K, ISHII T, KASHIWAGI S. Development of hub units with shaft clinching for automotive wheel bearings[J]. KOYO Engineering Journal English Edition, 2001, 158: 26-30.

[7]刘佳.轿车第二代轮毂轴承游隙与预紧力分析[J].上海汽车, 2010(3):44-47.

[8]黄维德，陈松海，靳阳，等.第三代轮毂轴承游隙的分析与检测[J].机电工程，2012, 29(10):1167-1170.

[9]《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京：机械工业出版社，1994:195-200.

[10] HAN X H，HUA L.3D FE modeling of cold rotary forging of a ring workpiece[J].Journal of Materials Processing Technology,2009,209:5353-5362.

[11] 梅怡. 梅花状径向铆接机的设计分析[J]. 制造技术与机床, 2012(9):53-56.

[12] QU J, ZHANG G J. Numerical and experimental investigations of the shaft-clinching assembly process of automobile wheel-hub-bearing units[J]. Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering, 2016, 230(13):1741-1757.